斜入射下1/4波片补偿能力的优化

陈思博， 周璇， 黄盆盛， 陈方中， 朱吉亮， 阮志毅， 霍丙忠*

（1.中国科学院 深圳先进技术研究院， 广东 深圳 518000；2.深圳市三利谱光电科技股份有限公司 研发中心， 广东 深圳 518107；3.河北工业大学 理学院， 天津 300401）

1 引言

对现代各类显示系统而言，偏振光偏振态的稳定传输是其能够展现出优秀显示效果的重要因素之一。理想状态下的垂直入射不必考虑斜入射时补偿膜相位延迟的改变，但在实际光路中，斜入射时入射光偏振态的传输与保持是影响视角、色差等现象的重要因素。例如虚拟现实（Virtual reality， VR）元宇宙设备，随着折叠光路光学系统的提出，设备逐渐向轻薄化发展，在其光机系统中，最重要的膜材之一便是1/4波片（Quarter wave plate， QWP）与反射偏振片。在近眼显示的实际场景中，屏幕所发出的光不可能永远保持垂直入射的状态，因此在大角度的斜入射状态下，偏振光经过补偿膜后偏振态的变化逐渐成为业界关注的焦点问题。除此之外，在有机发光二极管（Organic light emitting-diode display， OLED）显示屏等需要使用1/4波片的显示器件中，斜入射下1/4波片补偿能力的减弱也会造成大视角漏光及色偏等现象，影响最终显示效果。

根据Yang等人的研究［1-4］，斜入射下正交偏光片的漏光是不可避免的现象，其可以使用波平面的有效偏振角描述，而解决漏光最有效的方式便是使用补偿膜。将出射时偏振态偏离检偏器吸收轴的偏振光通过相位延迟补偿的方式，尽可能地被检偏器吸收。但是，引入补偿膜的方法同样会为系统带来二级问题：斜入射下补偿膜的相位延迟差异与色散［2］。补偿膜的相位延迟差异与波平面的有效偏振角类似，属于膜材本身的属性，一般很难改变；而色散则可以通过生产工艺进行控制。

RQWP膜材是一种拥有逆色散曲线的PC（Polycarbonate）材质1/4波片（日本Teijin公司生产）。对于一般的光学膜材而言，随着入射波长的逐渐增加，膜材本身所展现的相位延迟会逐渐降低，理想状态下膜材的相位延迟应该与入射光的波长成正比。换言之，随着入射波长的逐渐增加，相位延迟逐渐增加才能最大程度地保持偏振光偏振态的稳定传输［4］。RQWP拥有与理想逆色散曲线较为相近的色散曲线，但是斜入射下的偏振态保持仍然不尽如人意。

学术界有使用1/4波片和1/2波片（Half wave plate， HWP）叠加改善OLED反射色相的方案［5-6］，这种方案虽然使用两种膜材的“中和”效应使出射光尽可能地被吸收，但是对于膜材本身的折射率系数NZ（NZ=（nx－nz）/（nz－ny）=0.5，nx、ny，nz分别为膜材3个主轴方向的折射率）具有较高的要求，而补偿膜一般通过拉伸树脂原材进行生产，所以对生产制造工艺而言，折射率的精准控制是很难解决的问题。不仅如此，对于VR折叠光路而言，如果使用1/4波片+1/2波片的组合产生圆偏振光，则光路系统中偏振光的偏振态变化变得更加复杂，会增加光学设计的难度。因此，我们逐渐将目光转向面内折射率相同，厚度方向折射率存在差异（nz≠nx≈ny）的C-plate［7］。斜入射时，由于nz≠nx，C-plate厚度方向存在的相位延迟RTH（RTH=（（nx+ny）/2－nz）×d，d为膜材厚度）在理论上会对斜入射下偏振态传输稳定性的提升有一定的帮助。经过进一步的模拟和测试发现，通过使用C-plate可以将NZ≠0.5的补偿膜补偿至NZ=0.5的优异状态，这对于工业生产中直接生产NZ=0.5的补偿膜有很高难度的现实问题而言是一种较为有效而方便的尝试。综上所述，本文通过理论模拟加实验验证的方式，利用C-plate在厚度方向的相位延迟，探究了斜入射状态下C-plate对RQWP偏振态传输特性的优化。

2 理论方法与模拟结果

学术界对光在各向异性介质中的传播有大量研究［8-11］。对于偏振光在多层各向异性光学膜材之间的传输过程的研究，最实用的方法便是琼斯矩阵方法［12-15］。在琼斯矩阵中，偏振光与各类光学器件均可使用矩阵形式表示，而光在光学膜材中的传播过程也可在数学上通过矩阵相乘来表示。

但是琼斯矩阵也存在弊端。传统的琼斯矩阵只能计算入射光垂直入射至膜材堆叠时的情况，无法描述离轴状态。Berreman 4×4矩阵方法［16］则是较为全面的方法。虽然Berreman的方法能够精确描述多层膜之间的反射与透射，但是4×4矩阵往往需要更大量的科学计算与数学推导。本文使用A.Lien的扩展琼斯矩阵方法［13-15］计算斜入射下线偏振光通过双层膜材后出射光的椭圆率e，并通过e的数值判断出射光的偏振态。椭圆率e的范围为（0，1］。当e=1时，偏振光为圆偏振光；当椭圆率趋近于0时，偏振光为线偏振光；当0＜e＜1时，为椭圆偏振光。因此根据椭圆率的大小可以快速判断偏振光的偏振态，同时也可表征波片对偏振态传播的能力。

A.Lien开发扩展琼斯矩阵的最初目的是为了计算斜入射下扭曲向列相（Twisted nematic， TN）液晶盒的光学特性。在建模时，将一定厚度的TN液晶分为多层，每一层看作是液晶指向矢朝固定方向（光轴）排列的各向异性层。本文所研究的补偿膜同样为各向异性光学层，因此，A.Lien在文献中所描述的液晶分子指向矢方向即可认为是本文中所研究补偿膜的光轴方向。经过琼斯矩阵［17-18］的计算，对于出射光而言，其最终形式为式（1）所表示的琼斯矢量形式：

其中：δx与δy分别为偏振分量的相位，Ax与Ay分别为偏振分量的振幅。定义如下形式的复数χ，用于描述出射光的偏振态：

偏振椭圆的倾角α与椭圆度角β可用于描述偏振光的偏振态，定义如下［1-2］：

其中：Re［χ］代表实部，Im［χ］代表虚部，|χ|代表式（2）的模。根据式（2）～（4），椭圆率e可通过对椭圆度角β进行反三角函数计算解出：β=arctane。因此，可根据计算得出的出射光琼斯矢量分别提取其实部与虚部进行椭圆率e的计算。

本文使用两种RTH的液晶（Liquid crystal，LC）涂布型C-plate（Liquid crystal coated C-plate，LCC）LCC1、LCC2（日本DNP公司生产）与RQWP进行搭配测试，使用Axoscan相位差测试设备（Axometrics公司生产）实测3种膜材在550 nm入射光下的折射率，如表1所示。

根据表1中的参数以及上文提到的理论计算方法，我们使用Fortran语言进行编程和数值计算工作。在550 nm入射光的条件下，竖直线偏振光通过RQWP慢轴方向与入射光偏振方向呈45°的膜材堆叠后，出射光的椭圆率在RQWP、RQWP+LCC1和RQWP+LCC2三种情况下呈现出较大差别，如图1所示。

图1 根据实测数据所模拟的出射光椭圆率全辐角分布图Fig.1 Distribution diagram of the ellipticity of the outgoing light simulated according to the measured data

图1（a）、（b）、（c）分别为RQWP、RQWP+LCC1与RQWP+LCC2条件下出射光的椭圆率分布图。左侧纵轴为入射光的极角θ变化，圆周外的角度坐标代表入射光方位角ϕ的变化。图1中颜色越红代表椭圆率越趋近于1，颜色越蓝代表椭圆率越趋近于0。从图1不难看出，通过膜材的出射光椭圆率在全辐角范围内是连续变化的，并不会出现突变。

3种条件下图像整体均呈“斜十字”状。图1（a）中椭圆率e＞0.9的区域在方位角为45°、225°时可达到60°极角，而在135°、315°时为20°极角。对比图1（a）与（b）、（c）不难发现，LCC膜的存在会扩大椭圆率e＞0.9的区域。而不同RTH的LCC也存在差异。根据表1中的折射率数据，LCC1的RTH≈-95 nm，LCC2的RTH≈-125 nm，两种膜材存在大约30 nm的相位差。当入射光为斜入射时，光线在膜材堆叠中通过的实际距离l大于膜材堆叠的实际总厚度D。因此，图1（b）、（c）两图中，LCC膜虽然都可以扩大整体出射光的椭圆率范围，但是图1（c）在0°、90°、180°、270°方位角处、70°以上极角范围内仍然存在椭圆率e≈0.5的部分区域。从LCC1与LCC2的椭圆率模拟图中可以看出，LCC1对RQWP的优化效果要优于LCC2。

对于OLED或VR折叠光路的实际应用场景而言，斜入射光的入射角的定义在60°极角范围以内，所以本文后续的理论分析与实验验证均在45°极角、全方位角的条件下进行分析。将模拟数据中入射光以45°极角入射下3种膜材架构全方位角的椭圆率进行点线作图，如图2所示。

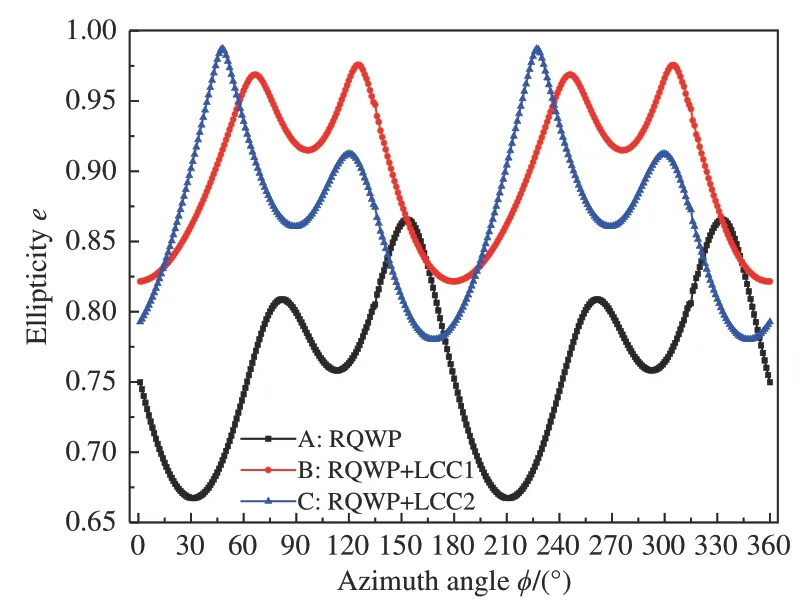
图2 入射光以45°极角入射后，出射光的全方位角椭圆率模拟分布图。Fig.2 Simulated overall angular ellipticity distribution of outgoing light after incident light at 45° poler angle

从图2可以明显看出，在入射光以45°极角入射时，RQWP在全方位角的出射光椭圆率峰值小于0.85，表明RQWP本身的圆偏振光转化能力在45°极角时有较大下降。而曲线B、C表明，LCC膜材确实能够提升RQWP在入射光大极角入射时出射光的椭圆率，能够使更多的圆偏振光出射，LCC2膜甚至还可以将最大椭圆率提升至1附近（图2中蓝色曲线），这也是实际应用中最想得到的结果。对比A、B曲线的峰值，LCC1能够提升10%的椭圆率，而二者对RQWP椭圆率的优化也存在差异，图1（c）中椭圆率e≈0.5的部分较图1（b）更大，从整体效果来看，LCC2要逊色于LCC1。在图2的B、C两条曲线中，C曲线的最大值ecmax=0.985 75，最小值ecmin=0.780 17；B曲线的最大值ebmax=0.975 82、最小值ebmin=0.821 6。不难看出ecmax与ebmax仅相差0.009 93，ebmin与ecmin相差0.041 43。对于整体效果而言，当两者最大值较为接近而最小值有明显差距时，LCC1膜展现了整体较为优异的椭圆率补偿特性。产生这一差异的原因与综合膜材RQWP+LCC1与RQWP+LCC2的折射率以及NZ系数［19］有很大关系。

根据文献［5］的报道，膜材折射率系数NZ=0.5时，1/2波片与1/4波片所组成的OLED圆偏光片具有最小的反射率，这就意味着NZ=0.5的圆偏光片能够出射更多的圆偏振光。而本文提到的两种综合膜材RQWP+LCC1与RQWP+LCC2通过LCC对RQWP在厚度方向的相位延迟补偿，也能够达到NZ趋近于0.5的特性。换言之，通过模拟与实测，我们发现可以通过LCC膜将NZ≠0.5的膜材调整至NZ=0.5，解决了工业生产中直接生产NZ=0.5的膜材难度大、不易控制等问题。我们分别测试了RQWP、PQWP+LCC1、RQWP+LCC2三种膜材架构的NZ，如表2所示。

表2 3种膜材的NZ数据Tab.2 Measured data of NZ of three films

从表2数据可以看出，LCC1膜材在与RQWP贴合一起后的整体NZ更接近0.5。为了进一步探究膜材的折射率性质，我们进行了NZ从0～1的一系列数学模拟，分别模拟了RQWP膜材在红（R）、绿（G）、蓝（B）3种波长下NZ变化所对应的椭圆率分布。分别选取470，550，620 nm对应蓝光、绿光、红光，结果如图3所示。

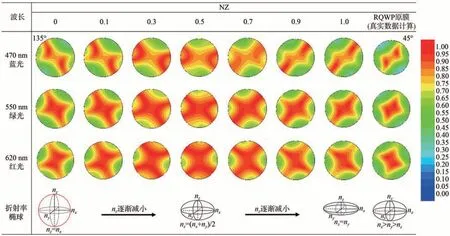
图3 入射光波长在470，550，620 nm下RQWP膜材NZ变化所对应的椭圆率分布理论模拟图。Fig.3 Simulated ellipticity distribution of RQWP under the variation of NZ within the wavelength of incident light at 470，550， 620 nm.

图3中最右侧一列为RGB三波长下RQWP椭圆率分布，其余列为NZ从0～1的理论模拟图。从图3结果可以明显看出，当膜材的NZ从0逐渐变化至1时，系统的椭圆率分布呈现一种从“倾斜的X型”到“均匀的X型”再到反方向“倾斜的X型”的变化趋势。470 nm和550 nm波长条件下的椭圆率变化趋势类似，而620 nm下的椭圆率变化呈现相反的结果。这是由于膜材本身在不同波段下的折射率分布，即色散造成的。RQWP膜材是一种PC材质拉伸得到的波长逆色散材料，随着波长的增加，膜材的面内相位延迟逐渐增大，在厚度不变的情况下，其折射率的差Δn=nx－ny逐渐增加。表3为使用Axoscan设备测试得到的三色波长条件下RQWP的折射率。

表3 RQWP在470，550，620 nm入射光下的折射率实测数据Tab.3 Measured refractive index data of RQWP under 470， 550， 620 nm incident light

根据表3中的折射率数据以及公式N=（nxny）×d/λ，实际的RQWP膜材在470 nm波长下N=0.283；在550 nm波长下N=0.260；在620 nm波长下N=0.237；而理想1/4波片的N=0.25，也就是RQWP膜材在470 nm和550 nm波段的相位延迟要大于λ/4，而在红光波段的相位延迟要小于λ/4。理论上，只有相位延迟等于λ/4时，线偏振光通过QWP才会转化为e=1的圆偏振光。进一步从折射率椭球上进行分析，当入射光垂直入射至RQWP时，相位延迟为RE=（nx-ny）×d。当入射光向nx方向倾斜时，由于nx＞ny，所以在nx和ny所组成的椭圆面中，只要入射方向非垂直入射，则n′x＜nx，即Δn减小，所产出的相位延迟RE′＜λ/4。反之，当入射光向ny方向倾斜时，所产出的n′y＜ny，最终的RE′＞λ/4。综上可知，当RQWP在470 nm和550 nm时，RE＞λ/4，那么在ny方向可以找到刚好使得RE=λ/4的区域，且该区域的椭圆率最大，这也就是RQWP在470 nm、550 nm两种条件下椭圆率在45°方向存在最大值区域的原因。同理，在620 nm波长条件下，RQWP在135°方向存在椭圆率最大值区域，如图3中最右侧一列所示。

图3还列出了RGB三色光RQWP膜材在不同NZ条件下椭圆率的理论分布模拟图。从图3可以清晰地看出，在NZ从0逐渐增加至1的过程中，e＞0.9的区域也呈现一种“从两边到中间”的变化趋势。在470 nm和550 nm两种条件下，当NZ=0时，e＞0.9的区域基本在135°的倾斜方向；当NZ=1时，e＞0.9的区域基本在45°的倾斜方向；而在NZ=0.5时，e＞0.9的区域呈现一个“X”型，基本能够覆盖最大的极角和方位角。在620 nm下的变化趋势与之相反但原理相同。从图3中折射率椭球所处一行也可以清晰地看出，膜材的NZ随着主轴折射率nz的减小而增大；而当nz=（nx+ny）/2时，NZ=0.5，说明当nz=（nx+ny）/2时，入射光以任意极角、任意方位角入射，在每一个折射率椭球的截面上的主轴折射率最小值即为（nx+ny）/2。这样一个平均的效应就导致在45°和135°方位角下，任意极角入射后出射光的椭圆率分布大致相同，椭圆率也就能在更多的极角、方位角条件下最大，这也是NZ=0.5最佳的原因。这一现象在RGB三色光条件下均能够得到满足，是一种宽波带的属性。所以，实测的LCC1膜比LCC2膜椭圆率补偿特性更优异的原因也正是因为RQWP+LCC1的NZ更接近0.5。因此，C膜厚度方向的RTH可以优化膜材本身对光偏振态传输的稳定性，同时可以根据理论计算选取合适的LCC材料将NZ≠0.5的补偿膜优化至NZ=0.5。

3 实验结果

根据上述模拟结果，我们希望通过实验来表征LCC对RQWP补偿能力的提升。对于RQWP在实际显示器件中的应用场景，我们采用OLED的圆偏光片模型进行环境光反射率和反射色相的测试。在OLED的圆偏光片［20］中，线偏振片与RQWP贴合在一起形成圆偏振片，可以将外界环境光在OLED电极结构上的反射光吸收，为OLED呈现任意角度完美的黑态，这也是“一体黑”的由来。其中的光学模型主要考察RQWP将线偏振光转化为圆偏振光的能力，因此与上文中的模拟计算较为契合。我们选取OLED圆偏光片进行实际的贴屏测试。

如图4所示，A、B、C分别代表以RQWP、RQWP+LCC1、RQWP+LCC2三种架构为基础制作的圆偏光片。图4（a）～（h）代表固定OLED屏幕位置不变，环境光为D65光源，从45°极角进行拍摄，方位角为0°、45°、90°、135°、180°、225°、270°、315°的实拍图。

图4 OLED屏幕贴屏图，极角45°拍摄。（a）～（h）不同方位角度拍摄，分别为135°、90°、45°、180°、0°、225°、270°、315°。图中A代表RQWP、B代表RQWP+LCC1、C代表RQWP+LCC2。Fig.4 Film on OLED screen， shot at a polar angle of 45°.（a）～（f） Shooting at different azimuth angles， 135°， 90°， 45°， 180°， 0°，225°， 270°， 315°， respectively. A represents the RQWP； B represented the RQWP+LCC1， and C represented the RQWP+LCC2.

从图4中不难看出，3种架构的膜材制成OLED偏光片之后，在不同视角下观察所反射的颜色差异很大。A膜材由于没有LCC膜的补偿，因此在不同方位角下观察时所呈现的反射颜色变化很大，从图4（a）、（b）的偏蓝到图4（c）、（e）的偏红，在图4（f）、（h）中A架构所表现出的红、蓝颜色差异也非常明显。虽然RQWP已经是逆色散的材料，但是其对垂直入射的可见光可能具有产生1/4相位延迟能力。一旦入射光以大角度斜入射，膜材本身的相位延迟变化可能不能够再次满足逆色散的属性。更多的椭圆偏振光出现，将导致漏光和色偏。相比于A架构，B、C架构在不同视角下的颜色变化略好一些，其中B架构要优于C架构，这与我们在第二部分中的模拟结果相同。从图4（a）～（h）不难发现，B架构的膜材基本能保证黑色，虽然也存在一定程度的色偏，但是颜色的变化整体不大；反观C架构，仍然在图4（f）、（h）中呈现偏蓝与偏红两种颜色。

使用CA410色彩分析仪（KONICA MINOLTA公司生产）分别采集了A、B、C 3种架构的OLED屏幕在45°极角、任意方位角条件下反射光的颜色信息，并将颜色的色坐标（采用CIE1931标准）绘制于图5中。在这个过程中，OLED屏幕被放置在暗室一个面内可旋转的平台上，该平台与桌面成45°倾斜，在平台的正前方存在一个D65光源。为了模拟自然光对OLED屏幕的光照情况，D65光源不需要进行准直处理。

图5 （a） 试验台简图；（b） 45°极角下3种架构贴OLED屏幕的全方位角反射光颜色坐标图。Fig.5 （a） Schematic diagram of the test worktable； （b）Color coordinate diagram of reflected light on OLED screens with three film stacks at a 45° polar angle.

在桌面的正上方设置一个CA410亮度色度计。当OLED屏幕在平台上旋转时，D65光源的光线以模拟日照的条件（点光源）均匀照射在OLED表面，经过表面的漫反射，CA410便可以接收OLED屏幕在45°极角、任意方位角条件下反射光的颜色信息，如图5（a）所示。

如图5（b）所示，A、B、C 3种架构在45°条件下反射光的颜色色坐标范围差异较大，其中A、C膜材架构的反射光色坐标范围相似，但C架构优于A架构。在A、C架构中，反射光的颜色色坐标范围覆盖了部分蓝色与红色区域，且A架构反射光的蓝色“更蓝”、红色“更红”（色坐标x、y更靠近0.26意味着颜色更蓝；色坐标x、y更靠近0.34意味着颜色更红）。这一现象与实际观察到的图4中A、C架构在不同方位角的反射颜色表现一致。B膜材架构的反射颜色落点较为集中（x坐标在0.3～0.32、y坐标在0.29～0.31），如图5（b）中红色圆圈表示。这意味着B架构的膜材在任何方位角下所看到的反射光的颜色整体变化不大，没有明显的偏蓝或者偏红的现象。这也与图4中B膜材架构的实拍图相符。

3种膜材架构的反射率曲线如图6所示。A膜材架构的反射率最高可达到9%左右，而使用LCC对RQWP进行补偿之后，整体反射率会下降至少2%。从图6中B、C曲线可以看出，LCC1膜材具有最佳的降低反射率的效果，全方位角的反射率在5.5%～6.5%之间，相比于A架构降低了约3%。

图6 45°极角状态下OLED贴屏实测全辐角反射率Fig.6 Measured full-argument reflectivity of the OLED screen at a polar angle of 45°

B、C两种膜材虽然都能降低反射率，但是结合图4、图5的反射颜色与反射颜色色坐标落点，B膜材整体要优于C膜材。这一结论与我们第二部分所得到的模拟结果相符。更低的反射率意味着更低的漏光，意味着光路中存在更多的圆偏光，也意味着架构整体的偏振维持特性接近理想状态。同理，更小的反射颜色色坐标范围则意味着看到的色偏更小，意味着“一体黑”的效果越好。

4 结论

本文通过理论与实验相结合的方式，探究了LCC对RQWP补偿能力的优化特性。通过理论计算了3种膜材架构的椭圆率分布。LCC1对RQWP椭圆率的优化效果最佳，椭圆率峰值ebmax=0.975 82。进一步测试得到RQWP+LCC1的综合NZ更接近0.5，通过理论模拟，讨论了NZ从0变化至1时，RQWP在RGB三色光条件下的椭圆率分布；得到NZ=0.5时，nz=（nx+ny）/2，该条件下椭圆率在任意极角、方位角时均有最大面积的椭圆率分布。而使用LCC补偿RQWP使得膜材综合NZ=0.5也是一种有效的快速得到NZ=0.5膜材的方法。

通过贴屏测试，OLED圆偏光片在有LCC补偿的情况下能够拥有更小的色偏与更低的反射率。其中LCC1架构的膜材整体色偏最小：x坐标在0.3～0.32、y坐标在0.29～0.31，且LCC1膜材架构的整体反射率下降了3%左右。通过理论计算与实验验证发现，LCC对RQWP补偿特性的优劣不仅与LCC本身的RTH有关，还与综合膜材的NZ有关，而本文所使用LCC对RQWP进行补偿的方法有助于将NZ≠0.5的膜材优化至NZ=0.5。由于在实际生产中直接生产NZ=0.5的膜材具有很高的技术难度，因此本文的研究结果对NZ=0.5的膜材开发提供了新的方法和可行路线。同时，λ/4波片的偏振调制能力在新型液晶光子器件的开发中也具有很广泛的应用［21］。本文的研究结果在相关器件的开发过程中具有潜在的应用价值。