对绳船模型中关联速度和加速度变化的深入分析




摘 要:从三个角度论证了绳船模型中的速度关系,用多种方法探究了船速率恒定和人收绳速率恒定两种情境下另一物体的加速度变化,最后分析了绳转动的角速度及小船在转动方向的加速度变化。
关键词:绳船模型;关联速度;加速度;微元法;函数
中图分类号:G633.7 文献标识码:A 文章编号:1003-6148(2023)9-0056-5
收稿日期:2023-01-03
作者简介:罗金龙(2000-),男,黄冈师范学院2020级本科生,主要从事中学物理、数学教育教学研究。
在运动的合成与分解相关知识的教学或学习中,我们常会遇到多物体的关联速度问题。而绳船模型是关联速度问题的一个经典模型,即一个人(或小车)在高为h的岸上用一根轻绳跨过定滑轮拉小船向岸边运动,这其中就涉及到人与船关联速度的分析,并且二者之间的关联速度也是定量研究运动过程中其他物理量的必要条件。不少教师在教学过程中让学生刻板记忆“将船速沿绳方向和垂直绳方向分解”的结论,学生往往不明所以,不利于其学科思维的养成和学科素养的提升。为了让学生不仅能“知其然”更能“知其所以然”,养成从物理学视角认识客观事物内在规律的科学思维,本文尝试从多个角度对绳船模型中的相关问题进行思考和探究。
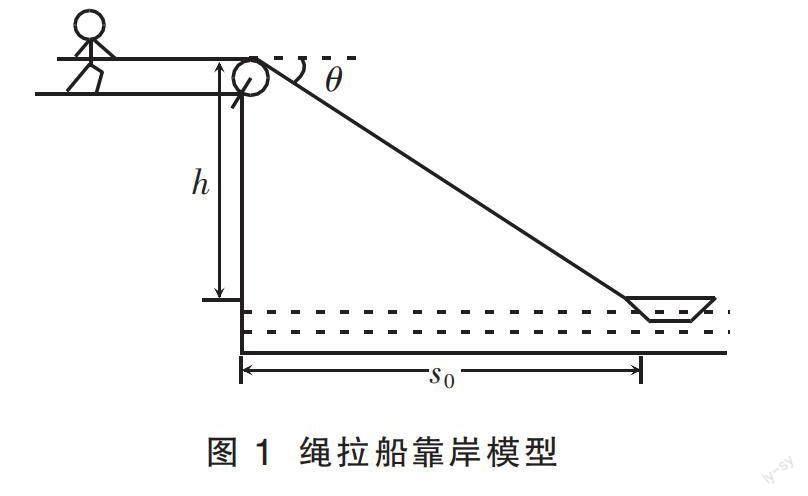
例题情境 如图1所示,湖中有一小船,初始时小船离岸边的距离s0足够远。人在距水面高度为h的岸上用一根不可伸长的轻绳跨过光滑定滑轮拉湖中小船向岸边运动,运动过程中滑轮右侧的绳子与水平方向的夹角为θ,滑轮左侧绳子始终保持水平。
1 三个角度理解关联速度
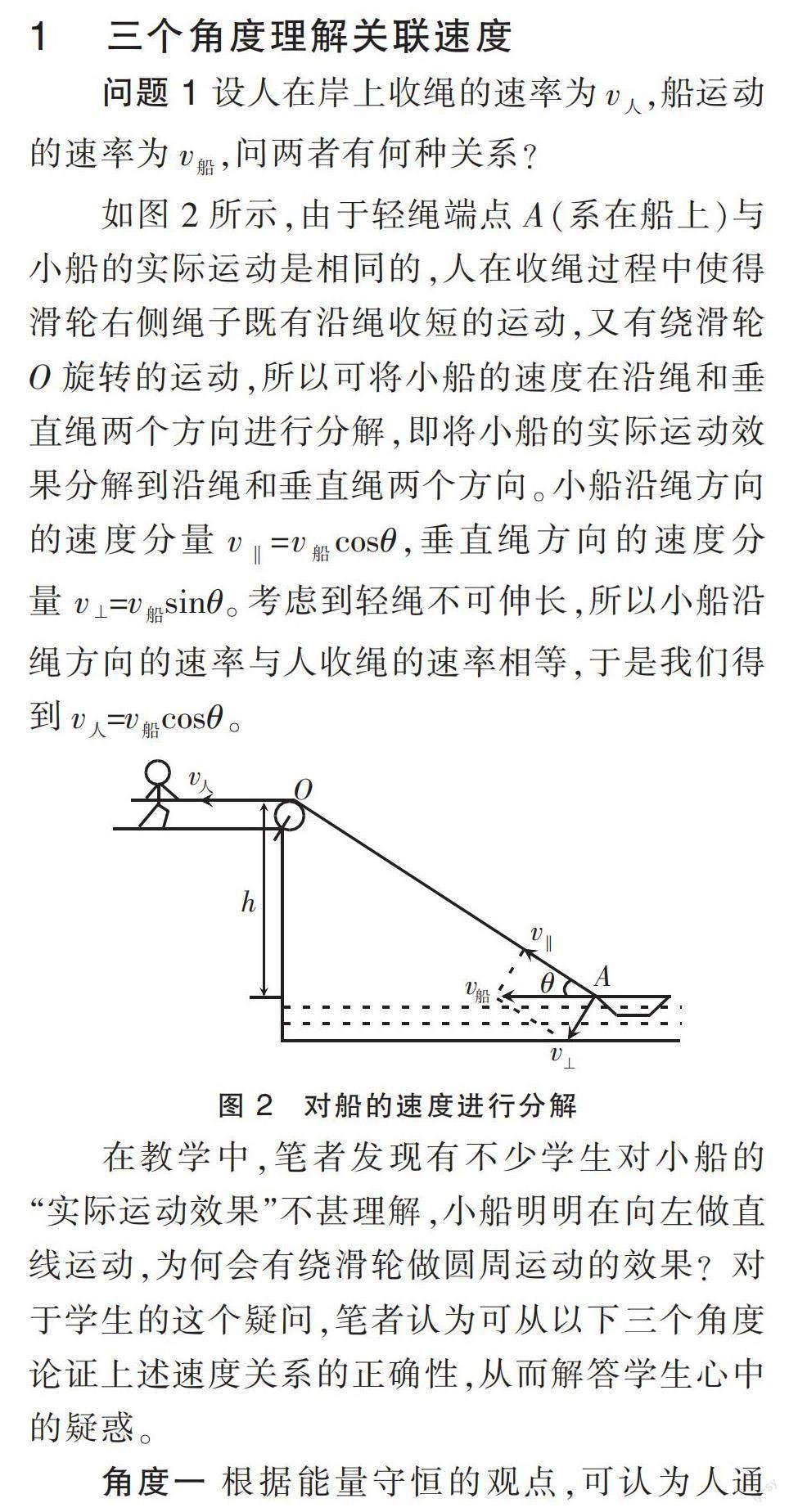
问题1 设人在岸上收绳的速率为v,船运动的速率为v,问两者有何种关系?
如图2所示,由于轻绳端点A(系在船上)与小船的实际运动是相同的,人在收绳过程中使得滑轮右侧绳子既有沿绳收短的运动,又有绕滑轮O旋转的运动,所以可将小船的速度在沿绳和垂直绳两个方向进行分解,即将小船的实际运动效果分解到沿绳和垂直绳两个方向。小船沿绳方向的速度分量v=vcosθ,垂直绳方向的速度分量v⊥=vsinθ。考虑到轻绳不可伸长,所以小船沿绳方向的速率与人收绳的速率相等,于是我们得到v=vcosθ。
在教学中,笔者发现有不少学生对小船的“实际运动效果”不甚理解,小船明明在向左做直线运动,为何会有绕滑轮做圆周运动的效果?对于学生的这个疑问,笔者认为可从以下三个角度论证上述速度关系的正确性,从而解答学生心中的疑惑。
角度一 根据能量守恒的观点,可认为人通过绳子输出的能量完全给了小船,即人拉绳的瞬时功率时刻等于绳对船的作用力的瞬时功率(图3)。假设轻绳中的张力大小为F,于是有Fv=Fvcosθ,得到v=vcosθ。
角度二 根据速度的定义,我们可先找出小船的运动方程。如图3所示,设小船运动过程中与岸边距离为s时,船与定滑轮之间的绳长为l。由几何关系有s2+h2=l2,式中s,l均为时间的函数,故两边同时对时间求导得2s=2l,其中=v,=v,于是得v=v=vcosθ。
角度三 根据微元法求解速度关系[1]。如图4所示,取小船向左运动过程中的一极小段时间Δt→0,则该过程轻绳绕滑轮O转过的角度Δθ→0,过B点作OA的垂线BE。由于Δθ→0,可认为OB=OE,即该过程人收绳的长度x=OA-OB=AE,小船向左运动的距离x=AB。可认为Δt内v和v均为定值,于是AE=vΔt, AB=vΔt,又AE=ABcosθ,同样得到v=
从三个不同的角度出发均得到了同样的结论,论证了将小船的速度分解到沿绳方向和垂直绳方向进而得到二者的速度关系这一做法是正确的。其中,角度一最为简单,从能量与功率的角度考虑绳船模型,将看似没有联系的两部分知识整合起来,体现了物理知识的连贯性和系统性;角度二从基本定义出发,能让学生结合具体问题加深对瞬时速度概念的理解;角度三的微元法是分析和解决高中物理中一些疑难问题的常用方法,其本质是一种微分思想,即将某个复杂的物理过程分成若干个小过程,而每个小过程往往遵循着最为简单的物理规律,从而使问题得到解决,有利于培养学生的科学思维。
2 对人收绳或小船的速度与加速度的分析
问题2 如图5所示,设小船以恒定速率v0靠岸,问人收绳的速率v和加速度a如何变化?
通过上文分析我们知道二者速度的关系为v=v0cosθ,由于小船在向左运动过程中夹角θ不断增大,即cosθ减小,所以人收绳的速率v在不断减小。对于加速度如何变化,笔者发现不少学生会直接将速度函数求导,即
a=v'=-v0sinθ(1)
从而得出加速度大小|a|在不断增大的结论。我们根据加速度定义a=不难发现这一方法其实是错误的。因为“-v0sinθ”实则是v关于θ的导函数,并非v关于时间t的导函数,因此并不符合常规加速度的定义。可从以下两个角度分析加速度的变化情况。
角度一 找v-t关系并绘制图像。
如图5所示,小船从初始位置开始向左运动的位移x=v0t,与岸边的距离s=s0-v0t,因此t时刻滑轮右侧绳长l=,又cosθ=,于是得到人收绳的速率与时间的关系为
v=v0=(2)
不妨取v0=1,h=2,s0=8,借助几何画板绘制出v-t图像及其导函数图像分别如图6中曲线Ⅰ、Ⅱ所示。从图中可直观看出,加速度在不断增大,加速度为负值表示与速度方向相反。
角度二 找a-t关系。可用以下两种方法得到人收绳的加速度与时间的关系。
方法一 函數求导法。
我们知道角度θ是时间t的函数,所以若将“v=v0cosθ”对时间求导,实则就是对一个复合函数求导,因此要先表示出θ与t的关系,由图5可知tanθ=,因此θ=arctan,所以=·=,又sinθ=,于是
从上式可知加速度a随运动时间t的增大而不断增大,负号表示a与v反向,即人收绳的速率v是加速度增大的减速运动。也可直接用(2)式对时间求导函数,所得结果与(3)式是完全一致的。
方法二 加速度等效法。
由于将小船的“实际运动效果”视为既沿绳方向运动又绕滑轮做圆周运动,因此可认为小船在沿绳方向具有向心加速度an。又因为小船在沿绳方向的速度分量v不断减小,因此存在一个与该速度分量反向的加速度a'n,即人收绳的加速度a,如图7所示。根据小船的实际加速度为零,于是有a'n=-an,又an===,则加速度
结果与上文相同。
将a=-与(1)式对比,也证实了(1)式的错误。虽然两式的结论都是加速度随角度的增大而增大,但其背后的原理却大相径庭,我们应避免类似错误的发生。
问题3 如图8所示,设人以恒定速率v1收绳,问湖中小船运动的速率v和加速度a如何变化[2]?
根据二者速度的关系知小船的速率v=,所以不难看出船速v随着θ的增大而增大。由于在问题2中我们主要从a-t关系入手研究加速度,且研究问题2的“加速度等效法”在小船做变速运动时并不适用,所以对于问题3小船的加速度不妨换一个思路进行研究。考虑到小船在向岸边运动过程中与岸距离越来越小,因此可尝试找出小船的加速度与离岸距离s的关系,从而得出加速度的变化情况,下面给出两种求解a-s关系的方法。
方法一 根据加速度定义对小船速度方程求导函数。
显然,随着离岸距离的减小,小船的加速度不断增大。
方法二 用微元法求解。
如图9所示,在小船运动过程中取一小段时间Δt→0,此过程轻绳绕滑轮转过一小角度Δθ→0,在A'点小船速度为v'A=,则Δt内小船速度增量Δv=v'A-vA=v1[-]。可认为,在Δt内船速在垂直绳方向的分量v=v1tanθ大小恒定,因此
对于问题3我们同样可以像问题2一样求解小船速度和加速度与运动时间的关系,只需根据滑轮右侧轻绳的初始长度和变化量表示出含有时间t的几何关系及三角函数关系即可。
3 对绳转动的角速度与船的切向加速度的分析
我们知道,小船在靠岸过程中有绕滑轮做圆周运动的效果,即滑轮右侧的轻绳在转动。为能判断其转动的快慢,我们不妨探究一下绳转动的角速度和小船在垂直绳方向的加速度如何变化。
当船速恒定时(问题2),小船在垂直绳方向的速度分量v=v0sinθ。根据v与角速度ω的关系可得ω===,所以随着小船的运动角速度在不断增大,即轻绳转动得越来越快。
小船在垂直绳方向的加速度at==·=v0cosθ·,根据角速度定义式=ω,因此
at的效果是使得v不断增大,这与v的变化情况是相符合的。根据问题2中“加速度等效法”的分析,我们知道应存在一个时刻与at等大反向的加速度a't,从而使得小船在垂直绳方向的实际加速度为零。如图10所示,可将小船的实际加速度a=0等效为四个分加速度an,a'n,at,a't,由于小船速度在两个方向的分量的大小和方向均在发生改变,所以不难看出各个分加速度的效果:at和an分别改变v的大小和方向,a'n和a't分别改变v的大小和方向[3]。
进一步分析at的变化情况。
令(6)式中sin2θcosθ=f(θ),可通过换元或均值不等式来求解f(θ)的变化情况,笔者给出一种不等式解法。(
首先,构造出多个和为定值的变量
根据均值不等式有(1-cos2θ)(1-cos2θ)·2cos2θ≤[]3=,于是得f 2(θ)≤,当且仅当cosθ=时取等,所以随着角度的增大切向加速度at先增大后减小,并在cosθ=处达到最大值。
當人收绳速率恒定时(问题3),相关分析与船速恒定类似,同理可得绳转动的角速度ω1==,结论与船速恒定时相同,即角速度在不断增大。小船在垂直绳方向的加速度at1=·=v1sec2θ·ω1=,因此当人收绳速率恒定时,小船在运动过程中切向加速度大小始终在增大。
综上所述,我们从多个角度、采用多种方法对绳船模型中的相关问题进行了分析,由浅入深,由易到难,既体会到了数学作为工具解决物理问题的重要性,也提升了分析问题的物理思维素养。
参考文献:
[1]王伟民,辛存良.用微元法求解牵连物体的运动速度[J].物理教学,2020,42(1):54-55.
[2]漆安慎,杜婵英.普通物理学教程 力学(第三版)[M].北京:高等教育出版社,2012:31-32.
[3]李柏涛.等效法在自主招生考题中的应用[J].物理教师,2013,34(12):90-92.
(栏目编辑 蒋小平)
