基于有限层法的承压水开采地面沉降简明分析

徐 进,张 豪,王斯海

(1.烟台大学土木工程学院,山东 烟台 264005;2.江苏工程职业技术学院建筑工程学院,江苏 南通 226000)

对含水层中地下水进行开采会破坏原有的水土平衡状态,在地下水位发生降深的同时,引发土层变形,导致地面沉降。同时,人类工程活动中对潜水和承压含水层的降水减压也会导致工程性沉降,对周围建筑物和市政设施造成不利影响。如何正确评估上述环境地质问题日益得到学术界的重视[1-2]。

从机理来说,地面沉降是一个复杂的流固耦合过程[3]。基于水-土耦合理论,LEWIS和SCHREFLER较早提出了地面沉降有限元计算模型,并运用于威尼斯的地面沉降问题[4]。HSI等考虑了潜水面变化,研究了抽水过程中潜水面变动对地面沉降的影响[5]。金小荣等利用二维有限元模型分析了工程降水作用下基坑周围土体沉降性状的影响因素[6]。骆祖江等系统建立了地下水开采引起地面沉降三维全耦合有限元模型,引入了渗透系数动态模型和邓肯-张非线性模型[7]。郑刚等利用有限元软件建立三维流固耦合模型研究了承压层长期局部降压的土体分层沉降机理和规律[8]。ZHOU等基于半解析数值原理给出了抽水作用下三维流固耦合问题的求解格式[9]。ZENG等建立了基坑降水地面沉降的耦合模型,分析了多层地下水系统基坑降水引起的支护结构和周围土体响应[10]。

但是,基于水-土耦合的地面沉降计算模型,由于计算工作量大、参数难以获取,在实际应用中仍受到一定限制。鉴于此,便于实际应用的简化计算方法得到较多关注。骆冠勇等基于一维太沙基固结方程,推导了承压水降压沉降的固结度计算公式[11]。龚晓南等结合地下水动力学公式与弹性半空间理论,给出了承压水稳定流情形下的最大沉降公式[12]。为了进一步反映抽水时间的影响,王春波等将其推广到了非稳定流情形[13]。

地下水流计算是地面沉降分析的基础环节,如何实现三维地下水流的高效计算一直备受关注。有限层法是一种典型的混合算法,兼具解析方法和数值方法的优点,其精确高效的特点在地下水流问题中已得到充分体现[14-15]。为此,基于地下三维流高效有限层方法,针对承压水开采引起的地面沉降问题,结合明德林解答和二维卷积公式,得到地面沉降的简明计算公式。借助Mathematica实现求解,验证计算公式的正确性,并对承压水降压下地面沉降的影响因素进行分析。

1 承压水三维流有限层法

图1所示为典型的下卧承压含水层,在其中利用抽水井开采地下水,在抽水井附近将出现地下水位降深,形成地下水的渗流运动。根据达西定律和质量守恒定律,抽水作用下引起的地下水三维非稳定流控制方程如下:

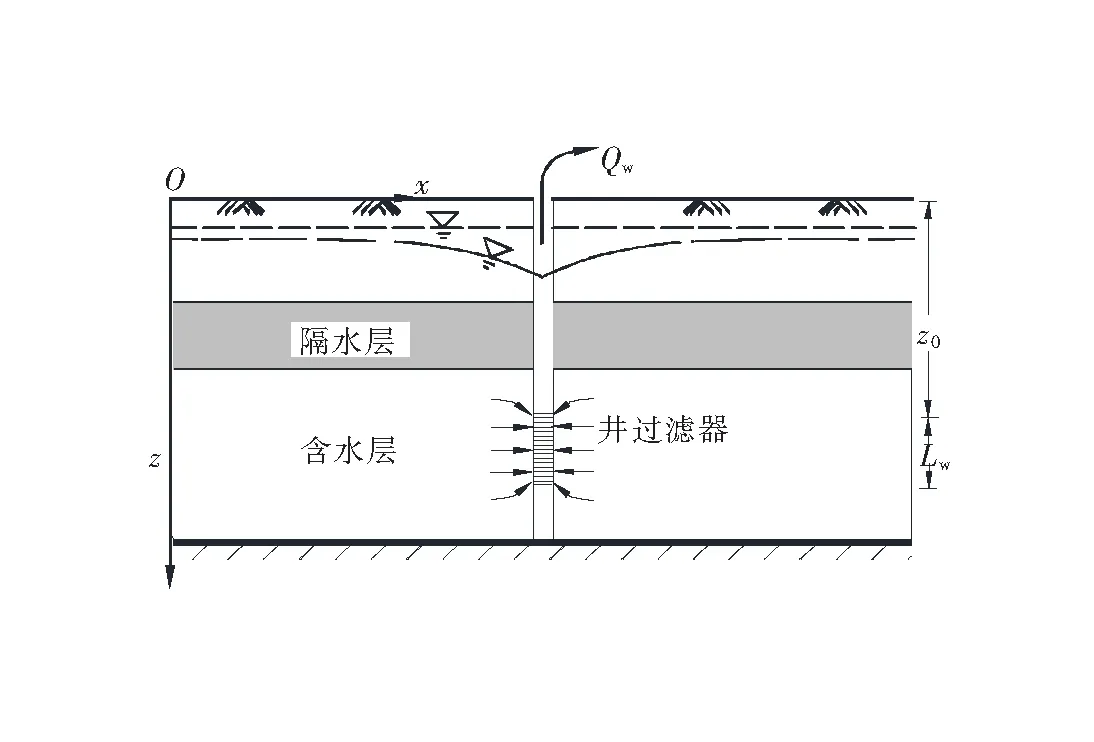
图1 承压含水层抽水井开采示意图

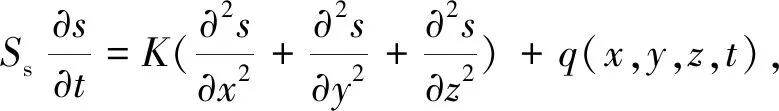
(1)

式中:s(x,y,z,t)为降深;K为含水层渗透系数;q(x,y,z,t)为汇源项;Ss为贮水率。

式(1)中q(x,y,z,t)表示单位时间从单位体积含水层中抽取的地下水量,表达式取决于抽水井的具体形式,对于图1所示的竖向非完整井,假如井中心位置为 (x0,y0,z0),则取如下形式:

q(x,y,z,t)=Q(z)δ(x-x0)δ(y-y0),

(2)

式中:

有限层法是一种介于解析法和数值法之间的混合算法。区别于计算域的全局离散,有限层法沿z方向将含水层离散成L个层元,水位降深在x、y平面采用正交完备的解析函数系{Amn(x,y)}表示,结合z方向的有限元形函数Nj(z),得到级数形式的降深试探函数[12]:

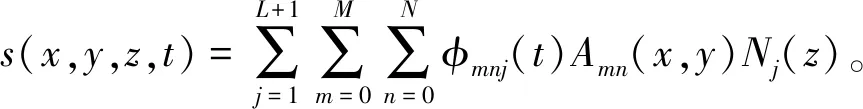
(3)

根据标准的有限元格式,得到关于未知系数的线性方程组:

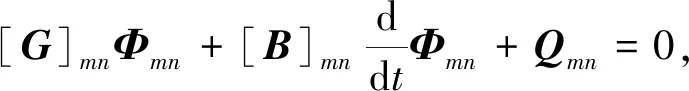
(4)

式中:Φmn={φmnj}为未知系数向量;渗透性矩阵[G]mn、贮水矩阵[B]mn和流量矢量Qmn可以由具有解析形式的公式计算得到,具体形式参见文献[14-15]。

在传统的数值方法中,数值积分是进行单元分析的必要环节,占到相当大的计算工作量。相比来说,有限层法不涉及数值积分,在地下水三维非稳定流分析时,计算工作量更低。同时,由于试探函数中解析函数的正交性,求解格式具有天然的解耦性,通过并行计算可以进一步提高计算效率[16]。

2 承压水开采引起的地面沉降

2.1 水位降深引起的附加应力

在抽水作用下,承压含水层中形成的降落漏斗将打破原有的平衡状态,导致上覆土层浮托力的减少,上覆土层底部(承压含水层顶板)形成竖向的附加应力, 这种由水位下降导致的竖向附加分布力为

f(x,y,t)=γw·s(x,y,0,t),

(5)

式中,γw是水的单位重度。

2.2 地面沉降计算公式

承压含水层顶板为隔水层,不用考虑含水层水位下降引起的潜水层越流和上覆土层的固结,地面沉降主要由含水层顶板处的附加作用力(5)引起。根据弹性力学的明德林解答可知,无限半空间体内,单位竖向集中力作用下,地表的竖向位移响应为

(6)

式中:E和ν分别为弹性模量和泊松比;h是上覆土层的厚度。

基于二维卷积公式,结合单位集中力位移响应(6)和级数降深函数(3),可以得到分布力(5)作用下的地表沉降计算公式

w(x,y,t)=

w′(x-η,y-θ)dηdθ。

(7)

利用地下水流的有限层求解格式(4),将得到的降深级数计算解代入式(7)进行积分,可以分析抽水作用下的地表沉降过程。如果需要对土层内部的位移、应力等情况进行分析,可以用相应物理量的明德林解在式(7)中对地表沉降w′进行替换。式(7)难以进一步展开成解析形式,本文利用Mathematica进行求解。

3 对比验证与影响因素分析

3.1 对比验证

为了验证该方法的正确性,选取典型算例进行了分析,其中下卧含水层中抽水井为完整井,地下水流为稳定流。图2给出了不同弹性模量取值(E=1 MPa, 2 MPa, 5 MPa)下,地表中心沉降w0随覆盖层厚度变化的计算结果,并将其与已有解进行了对比。可以看出,三种情况下本文给出的计算结果都与已有解[12]吻合良好,验证了本文方法的正确性和合理性。同时,图2计算结果也反映了上覆土层厚度h对地面沉降的影响,在特定弹性模量取值下,随着h的增加,含水层埋深越大,地下水开采的影响越小,所引起的地表沉降越小。当土层厚度h=30 m,泊松比ν=0.4,E=1 MPa时,在承压水降深s=15 m的条件下,地面中心沉降接近0.015 m,这与文献[12]中江南工作井的计算和实测结果相吻合。

图2 地表中心沉降随覆盖层厚度的变化

地下水开采是地面沉降发生的诱因,本文研究了开采量对地面沉降的影响,见图3。可以看出,开采量对地面沉降具有直接影响,随着开采量的增加(Qw从500 m3/d增加至1000 m3/d),地面沉降明显加剧,中心沉降从0.013 m增大到接近0.27 m,两者呈正相关,保持良好的线性关系。因此,结合当地水文地质条件,特别是开采含水层的补给条件,制定合理地下水开采量是地面沉降灾害预防的关键。

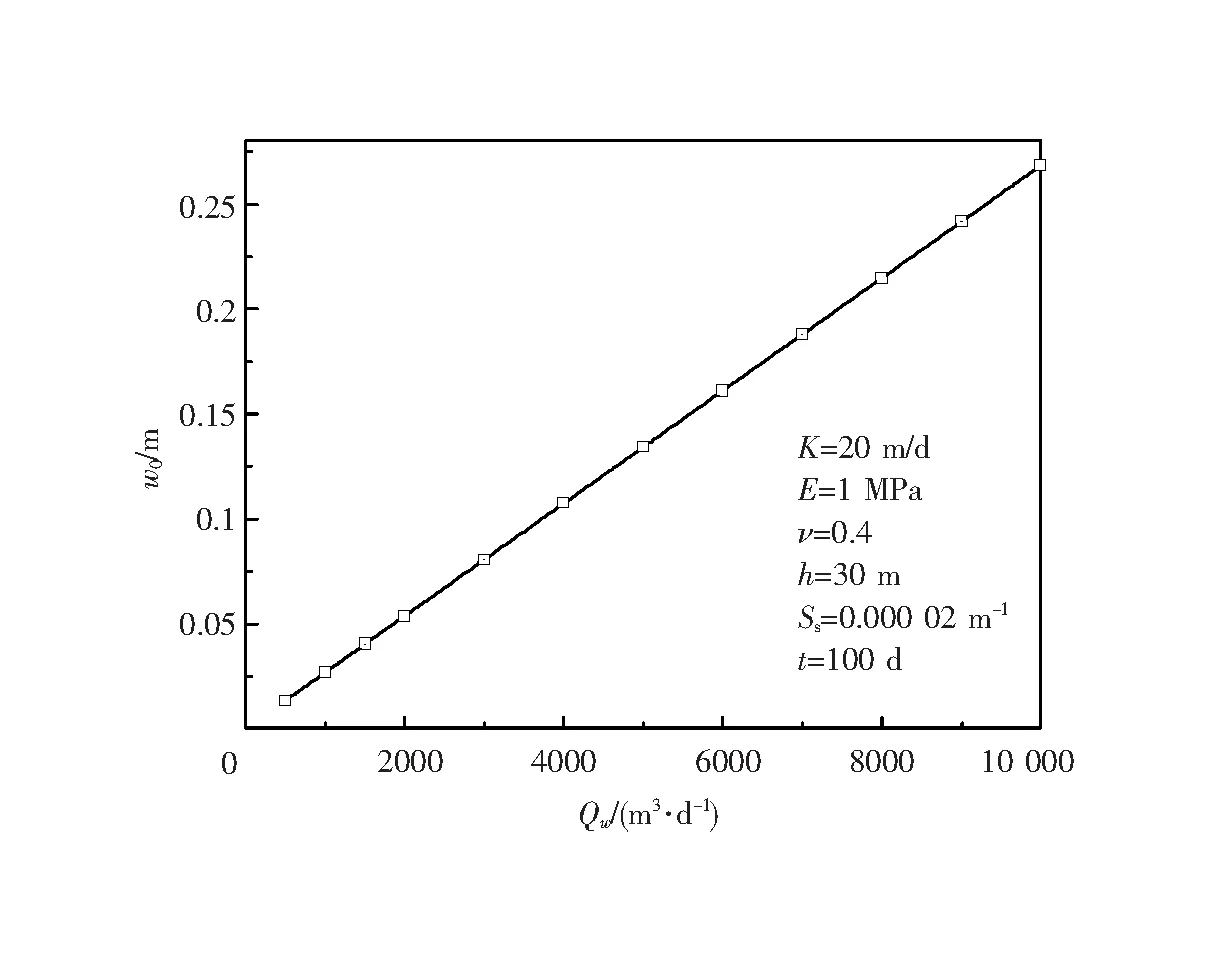
图3 抽水量对地面沉降的影响

文献[12]的地面沉降计算公式可以分析中心沉降,不能给出地面沉降的空间分布。利用本文方法给出了抽水井附近的地面沉降分布,如图4所示。可以看出,竖向单井抽水作用引起的地面沉降呈漏斗状分布,与水位降深分布保持一致,最大沉降出现在抽水井中心,随距井径向距离r的增加逐渐减小。同时,由于本文方法中考虑了地下水的非稳定流,可以给出地面沉降的发展过程,图4给出了不同时刻(t=0.5, 1, …, 10, 20 d)的沉降曲线,可以看出,随着抽水时间的延续,井附近的地面沉降不断加剧。

图4 地面沉降随抽水时间变化

3.2 影响因素分析

地面沉降涉及地下水运动和土体变形的相互作用,影响因素很多。本文计算公式建立过程中,虽然采用了一定简化(忽略上覆土层的固结变形),却考虑了一些重要水文地质参数(如渗透系数K和贮水率Ss)与土力学参数(如弹性模量E和泊松比ν)的影响。

图5给出了渗透系数K对沉降的影响,可以看出,K数值越大,含水层内水力联系越强,井附近的水位降深越均匀,中心沉降和差异沉降越小。图6表明含水层贮水率Ss对沉降也有显著影响,随着Ss的增加,含水层中的地下水储量越大,抽水作用下含水层内的水位降深越小,所引起的沉降值也越小。

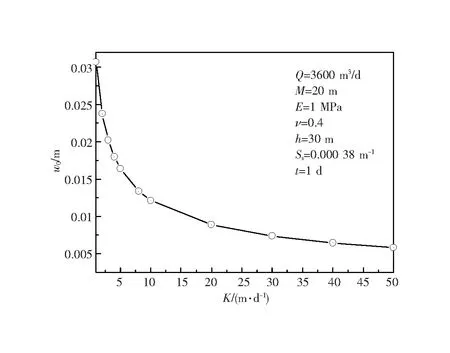
图5 渗透系数对地面沉降的影响

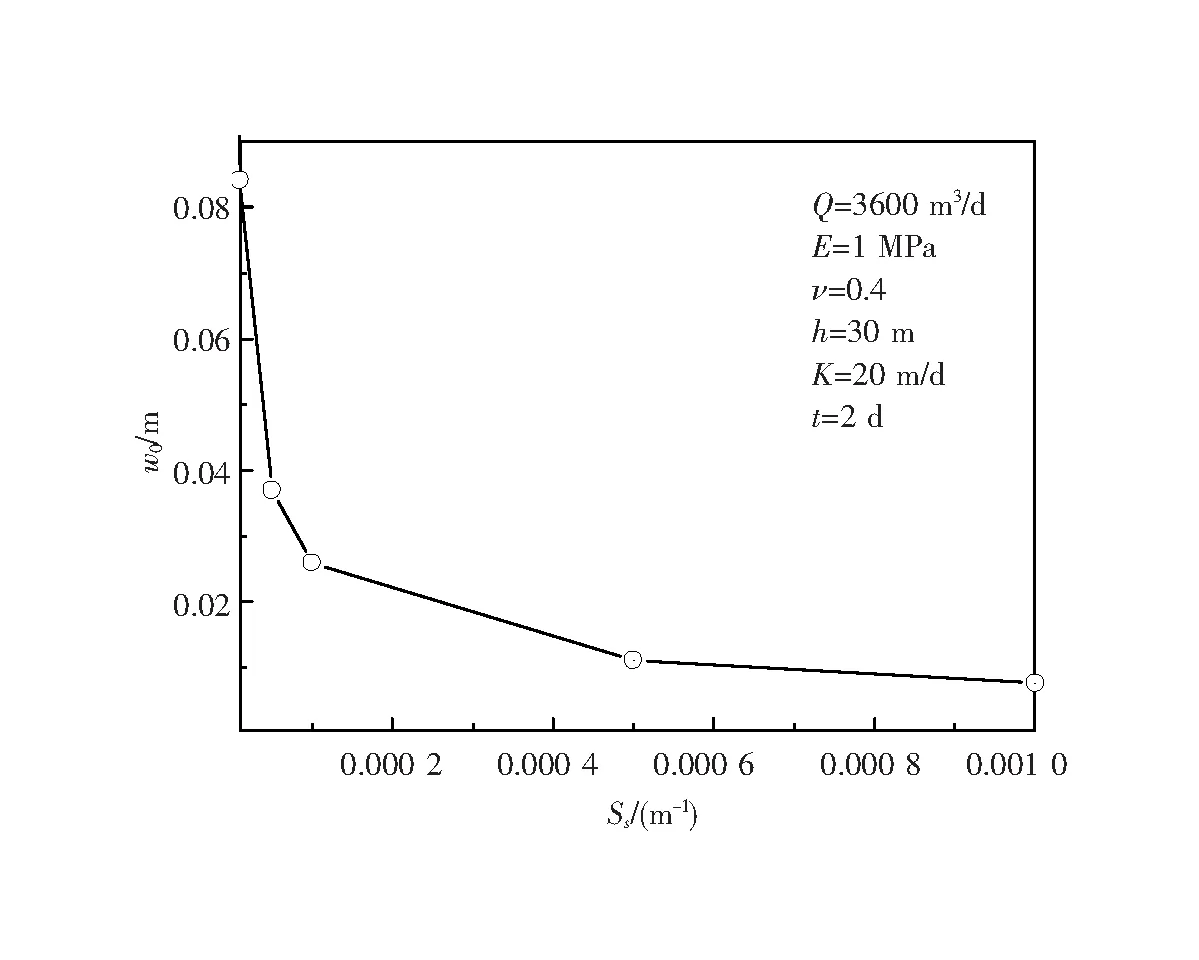
图6 贮水率对地面沉降的影响

图7和图8给出了上覆土层力学参数的影响,可以看出,其他条件保持不变的情况下,覆盖土层刚度越大,土体变形越小,沉降量越小,当弹性模量E从1增加到10 MPa时,最大沉降量下降了87.5%;相对而言,泊松比ν对沉降的影响较小,当ν在从0.15增加到0.55时,最大沉降值减少了25%。

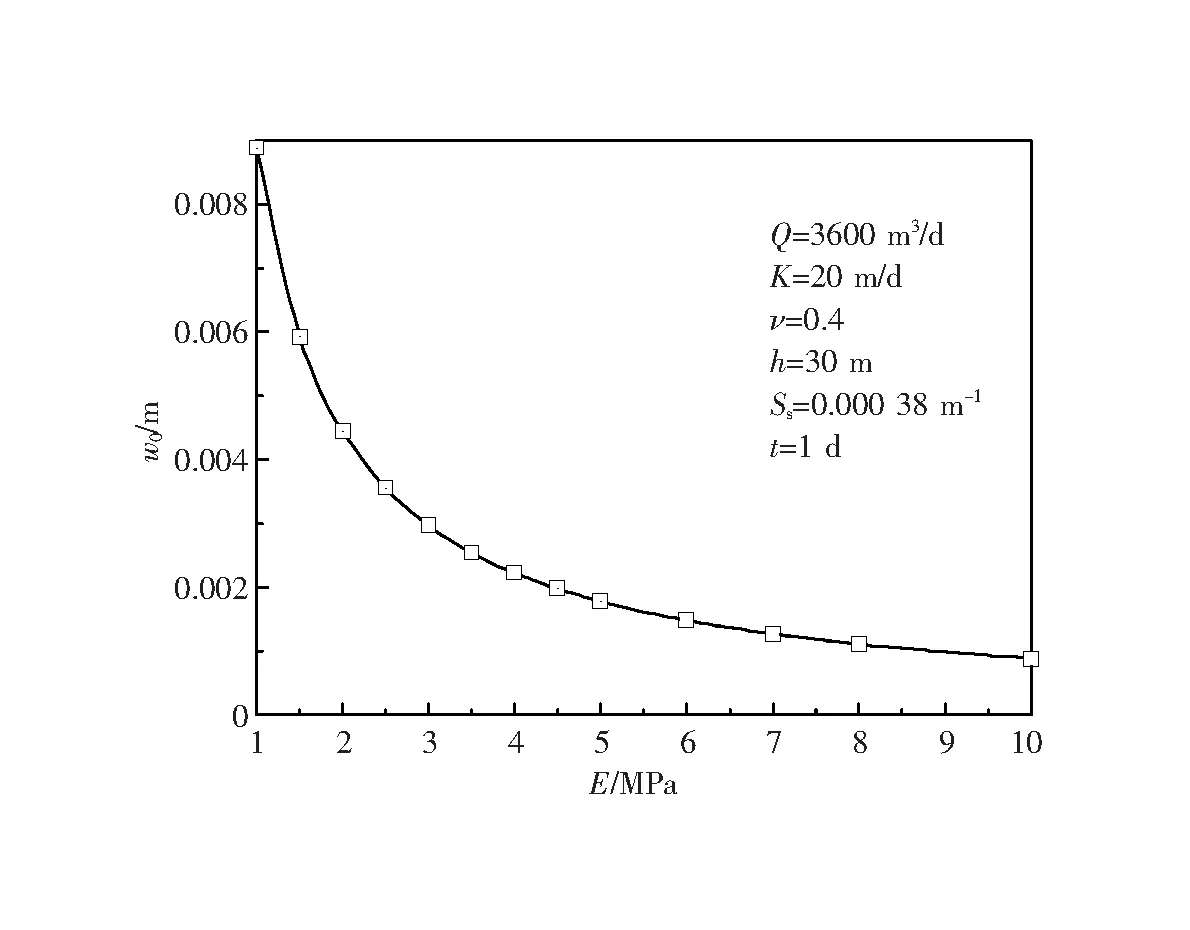
图7 弹性模量对地面沉降的影响

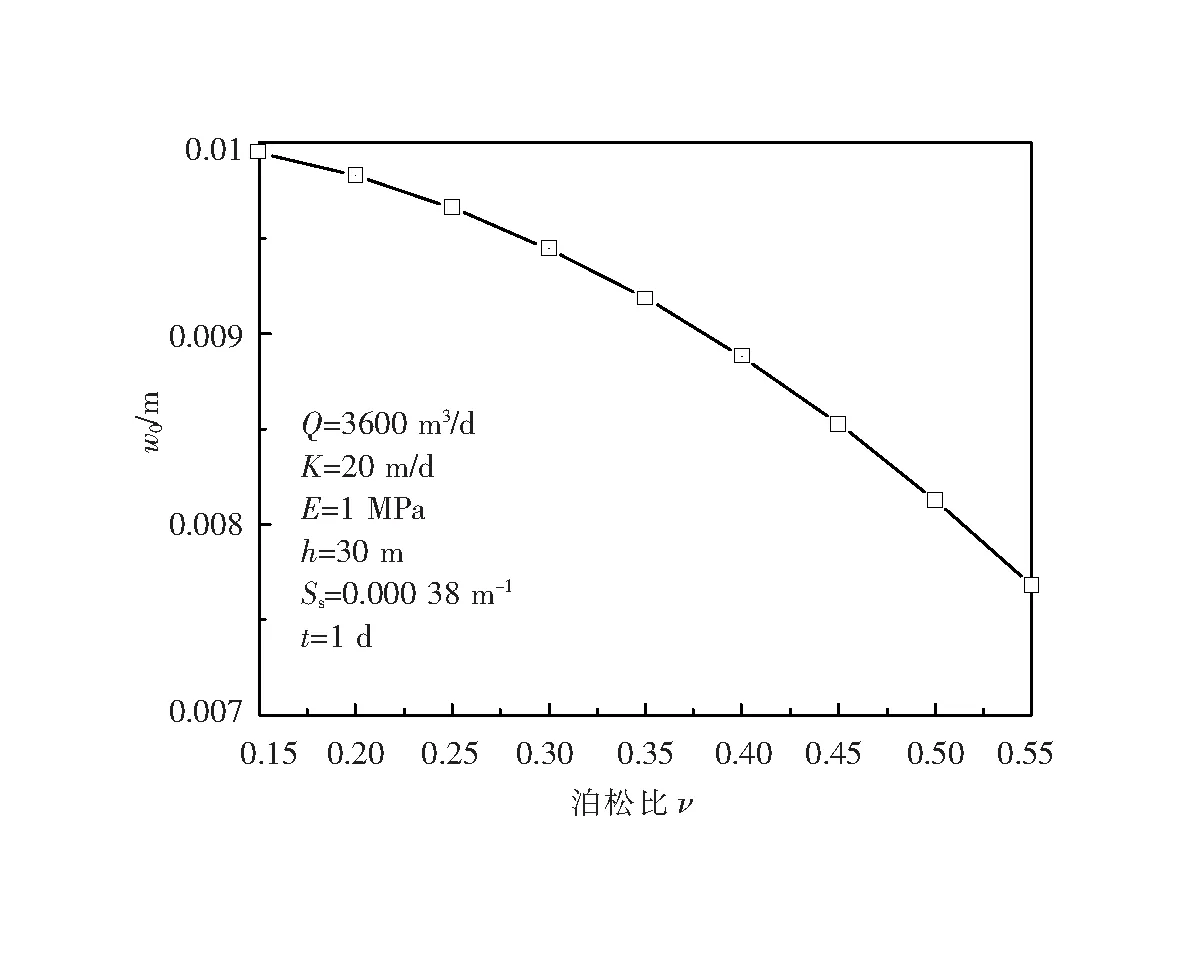
图8 泊松比对地面沉降的影响

3.3 多种抽水形式下的地面沉降

近年来,水平井凭借比常规竖向井更高的抽水效率,在环境和水文方面得到越来越多的应用[17-19]。与普通的井网结构不同,水平井的井过滤器水平放置(图9)。在地下水运动特征上,一般来说,水平井引起的水流模式比传统竖向井更加复杂,具有明显的三维流,并缺乏轴对称性[20]。

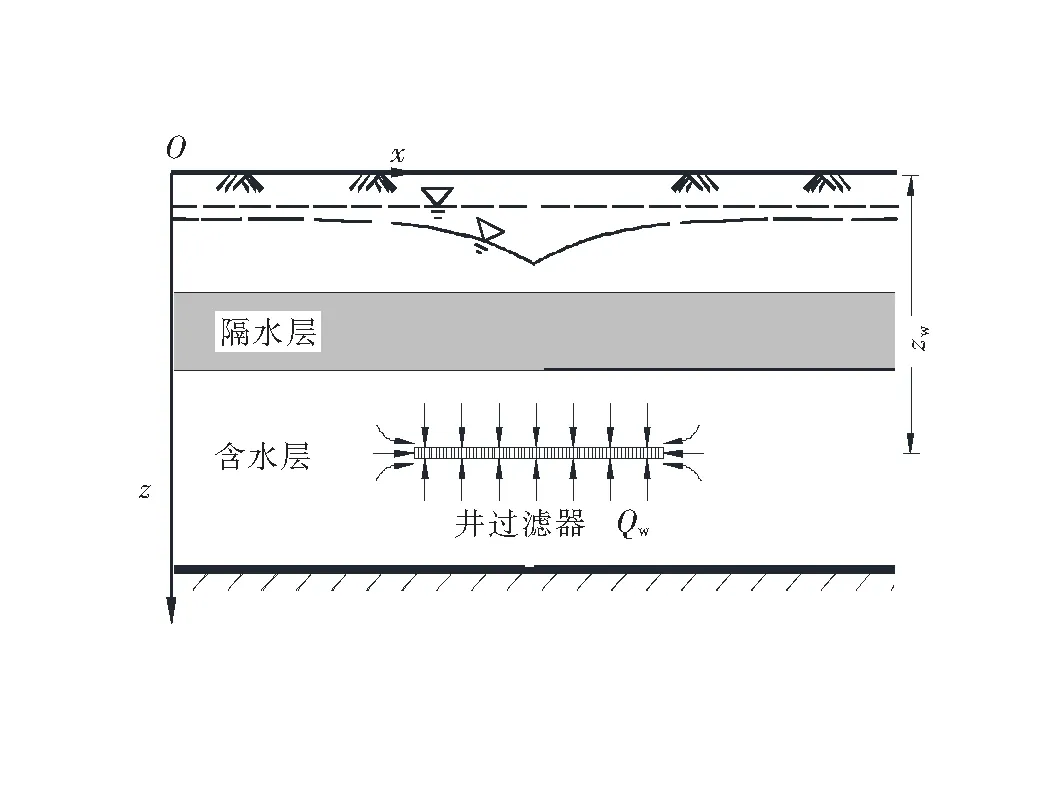
图9 含水层中水平抽水井示意图

在有限层求解格式中,水平井过滤器可以完全嵌入剖分节面,从而只需对求解格式(4)中{Qmn}进行适当修改,无需离散就可以实现求解[15]。基于本文方法,水平井附近的地表沉降曲线如图10,为了便于对比,图中也给出了相同抽水量下竖向井的地表沉降分布。可以看出,相比于竖向井,水平井开采引起的地表沉降不存在轴对称性,沿过滤器方向的沉降和垂直方向的沉降并不一致,沿井轴方向沉降值更大。此外,总体上,水平井引起的沉降分布比竖向井更为平缓,这与水平井的水力学特征相吻合[15, 20]。

图10 水平井和竖向井引起的地面沉降分布曲线对比

为了优化开采方案,在含水层中通常会设置群井系统。在传统有限元数值方法中,为了获得精确的近井水流模拟结果,每一个抽水井附近,都需要更精细的网格划分,这会带来额外的工作量,甚至造成网格不规则和离散误差。有限层法中,由于采用具有解析表达式的流量矢量Qmn代替网格划分,不存在上述问题,因此在处理多井问题时更加方便。

为了说明本文方法处理多井问题的能力,设计了由三口竖向井和一口水平井组成的群井系统,具体计算参数见表1。图11给出了群井开采下地面沉降的等值线图,可以看出,在抽水井附近形成了四个局部沉降锥。三口竖向井附近的等高线近似于同心圆,水平井附近的等高线为椭圆,正确反映了竖向井和水平井的水力特性,说明了本文方法应用于群井问题的适用性。

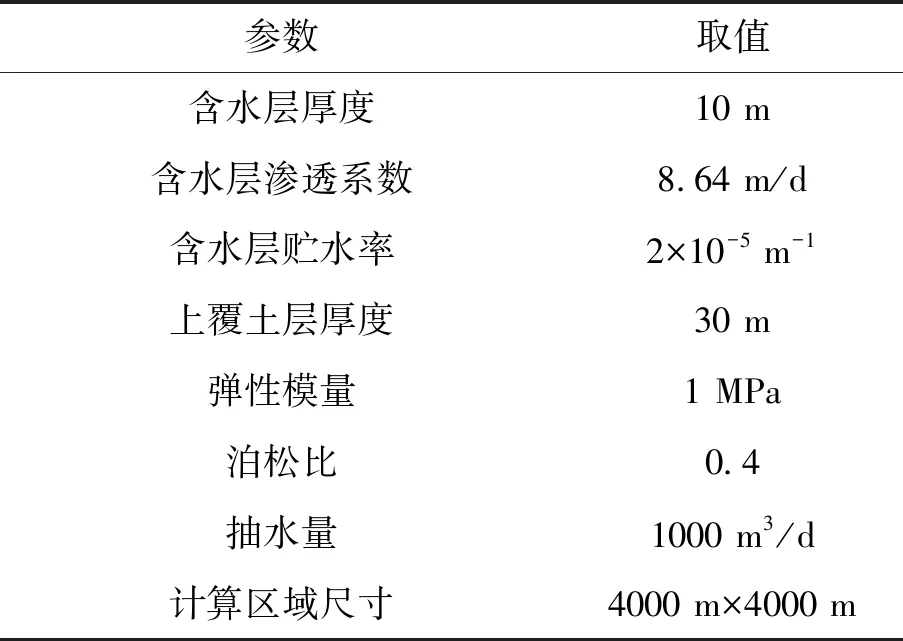
表1 群井问题计算参数

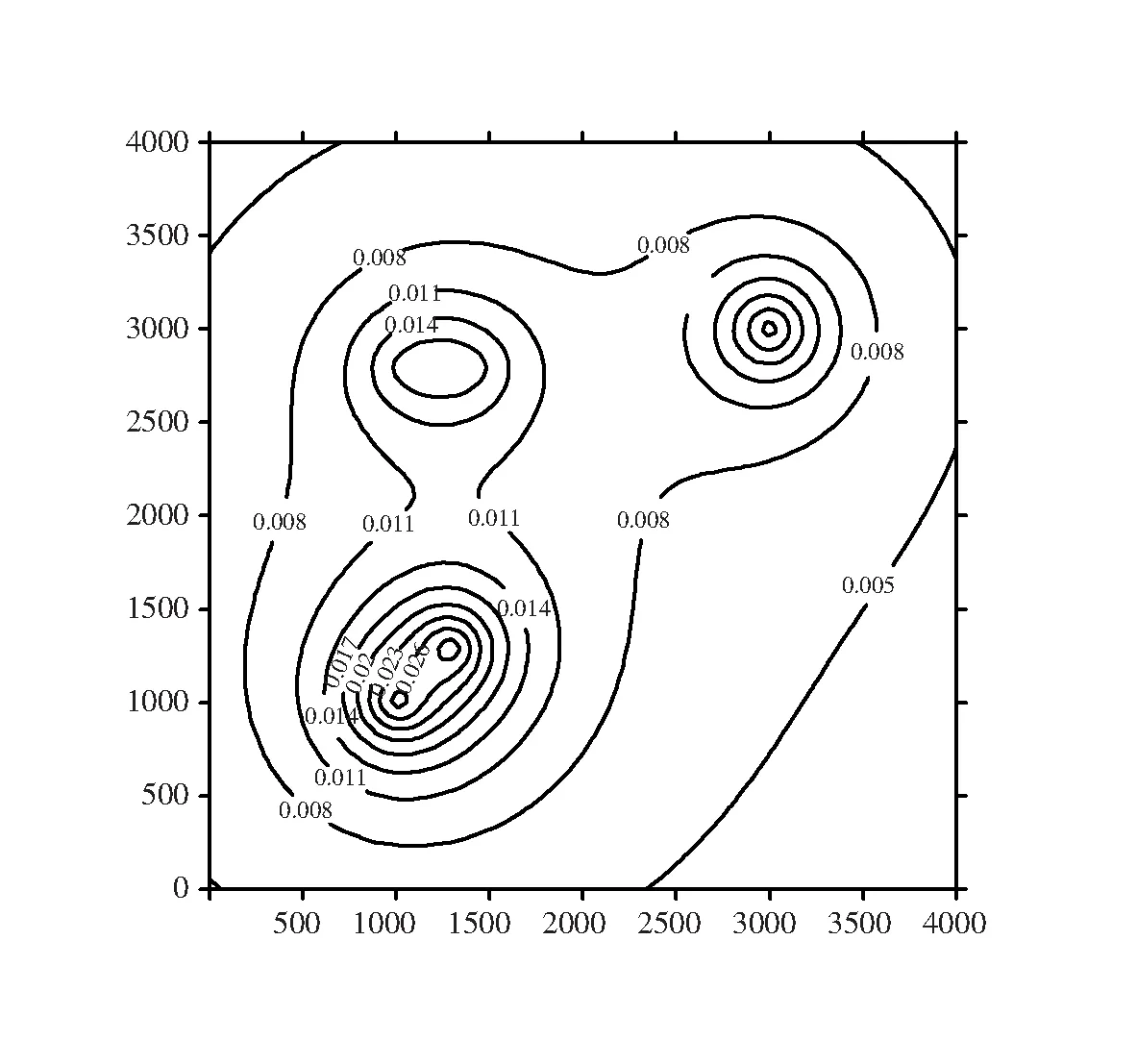
图11 多井抽水地面沉降等值线

4 结 论

针对开采承压水诱发的地面沉降问题,基于地下水三维非稳定流的有限层方法,利用二维卷积公式和弹性半空间明德林解,提出了一种简明的地面沉降计算方法。通过与已有解的对比,验证了本文方法的正确性。本文简化计算公式可以反映地面沉降的空间分布及其时间演化过程。通过算例分析,研究了多种因素对抽水地面沉降的影响规律,结果表明:(1)上覆土层厚度越大,地面沉降量越大;弹性模量对地面沉降影响较大,覆盖土层刚度越大,地面沉降越小。相对而言,泊松比的影响较小;(2) 含水层渗透系数和贮水率对地面沉降也有一定影响,渗透系数越大,含水层内水力联系越强,差异沉降越小;含水层的储水量越大,地面沉降越小;(3) 对水平井、群井问题进行了分析,所得结果符合相应的水力学特征,说明该方法在处理复杂抽水问题时也具有一定的适用性。