基于强化学习的非线性主动悬架系统的最优控制
张皓涵,崔明月
(烟台大学数学与信息科学学院,山东 烟台 264005)
随着汽车技术的不断发展,对汽车的操纵稳定性、车内人员的舒适性和隔绝道路颠簸等起重要作用的悬架系统受到了极大的关注[1],相较于被动悬架和半主动悬架[2],主动悬架系统因其可通过设计控制器较好地改善乘坐舒适性和车辆的机动性被广泛应用。随着控制技术的发展,提出了许多不同的驱动器控制策略[3-6],如自适应控制、鲁棒控制、模糊控制和智能控制等。然而多数文献中均假设悬架系统具有线性动力学特性,事实上悬架弹簧和阻尼器具有非线性特性,对于非线性主动悬架,许多学者发展了诸如自适应、鲁棒制和滑模等控制策略[7-9],使得系统达到跟踪或镇定。
众所周知,悬架系统的作用不仅是要隔振,而且还要提高车辆性能。针对悬架系统的这一问题,人们提出了主动悬架最优控制方法[10],然而现有的最优控制策略[11-15]大多是针对具有线性动力学特性假设的悬架系统。对于非线性最优控制问题最大的挑战是求解哈密顿-雅可比-贝尔曼(HJB)方程,然而求解HJB方程是非常困难甚至是不可能的,为了解决这一问题,贝尔曼在文献[16]中提出一种动态规划理论。文献[17]利用神经网络给出了HJB方程的近似解,文献[18-19]中借助于强化学习算法,用Actor-Critic框架实现在线实时学习最优控制设计HJB方程的解,文献[20]利用此方法解决无人船的最优跟踪控制问题。受此启发,本文研究了基于强化学习的非线性主动悬架系统的最优控制问题,主要工作如下:
(1) 最优性能指标直接影响车辆性能和乘客舒适性。基于所建立的非线性模型,综合考虑车身加速度,悬架扰动度和轮胎的位移等因素给出了合理的代价函数,然后利用非线性最优控制理论设计了初始最优控制策略。
(2)针对最优控制中求解HJB方程的困难,借助于强化学习的Actor-Critic框架提出了一种新颖的在线实时学习HJB方程近似解的策略,同时为提高系统的鲁棒性,在Actor-Critic更新率中增加了泄漏项。
(3)通过李雅普诺夫稳定性理论分析表明,所提策略使得主动悬架系统的位移终极有界,且边界可以通过调节参数充分小从而实现实际稳定,同时使代价函数达到最优。
1 问题提出
考虑如图1所示的行驶在崎岖路面上的1/4汽车主动悬架系统。车轮和车身的质量分别为Mc和Mb,位移分别为s1和s2。车轮与车身之间的控制器u,线性弹簧和非线性阻尼器是并联的,其中弹簧系数为Ka,阻尼系数为Ca。车轮看作是弹簧系数为Kt的线性弹簧。s0为崎岖路面对系统产生的干扰位移。
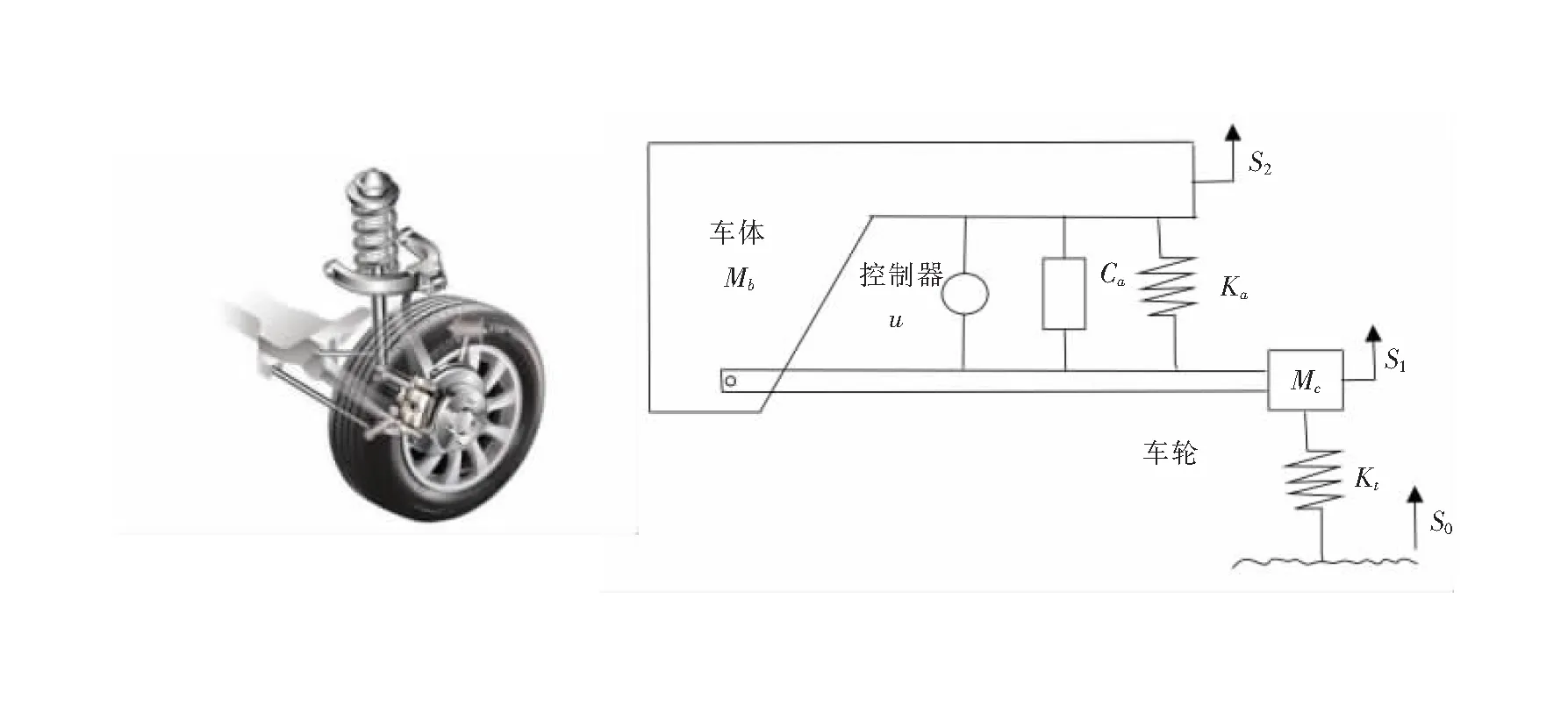
图1 1/4汽车主动悬架模型
考虑以车轮和车身组成的质点系,选取(s1,s2)作为广义坐标,则系统的总动能和总势能分别为
(1)
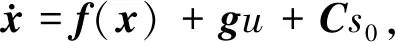
(2)
其中,x=[x1,x2,x3,x4]T,C=[0,0,0,-Kt/Mc]T为路面输入位移参数阵,
显然f(x)满足局部Lipschitz条件并且f(0)=0,即对于给定的M>0,存在LM>0 使得
‖f(x)‖≤LM‖x‖,∀x∈ΩM,
(3)
其中ΩM={x∈4| ‖x‖≤M}。g是有界的,即‖g‖≤bg,其中
(4)
其中q4>0是加权系数。
令
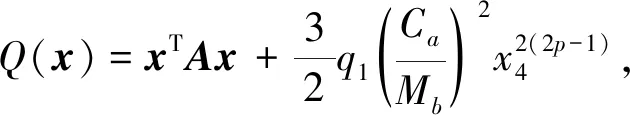
(5)
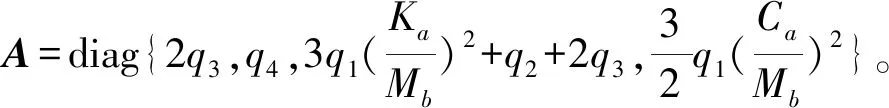
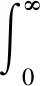
(6)
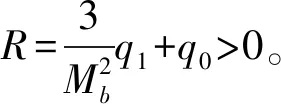
控制目标:设计一个控制器使得系统状态s1,s2能够收敛到充分小的范围内,并且系统的代价函数J达到最优,以保证车辆的舒适性和驾驶的安全性。
为了完成控制目标,需作如下假设:
假设1崎岖路面对系统产生的干扰位移是有界的,即存在一个常数b>0,使得|s0|≤b。
2 基于强化学习的控制器设计
2.1 最优控制
下面将设计控制器u使J最小。最优代价函数:
(7)
根据最优控制原理[23],J*和最优控制u*满足HJB方程

(8)

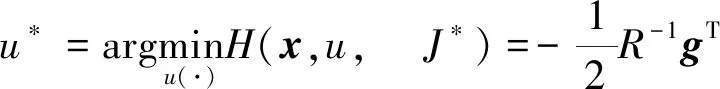
(9)
众所周知HJB方程(8)求解非常困难,甚至是不可能的。为解决这一困难,下面将最优的代价函数J*由神经网络逼近
J*(x)=W*Tφ(x)+ε*(x)=φT(x)W*+ε*(x),
(10)
其中,ε*为逼近误差;W*∈N为理想的权重矢量,N为神经元数量;φ(x)=[φ1,φ2,…,φN]T为初值为零的基函数。则J*(x)关于x的梯度为

(11)

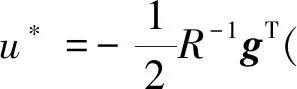
(12)
若用
(13)

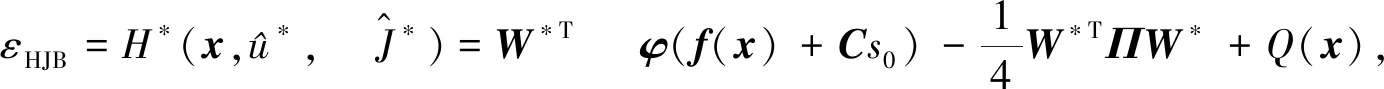
(14)

2.2 Actor-Critic设计
由于理想的权重矢量W*实际是未知的,则估计式(13)不能用。下面将借助于Actor-Critic算法修正估计式(13),结构如图2所示。
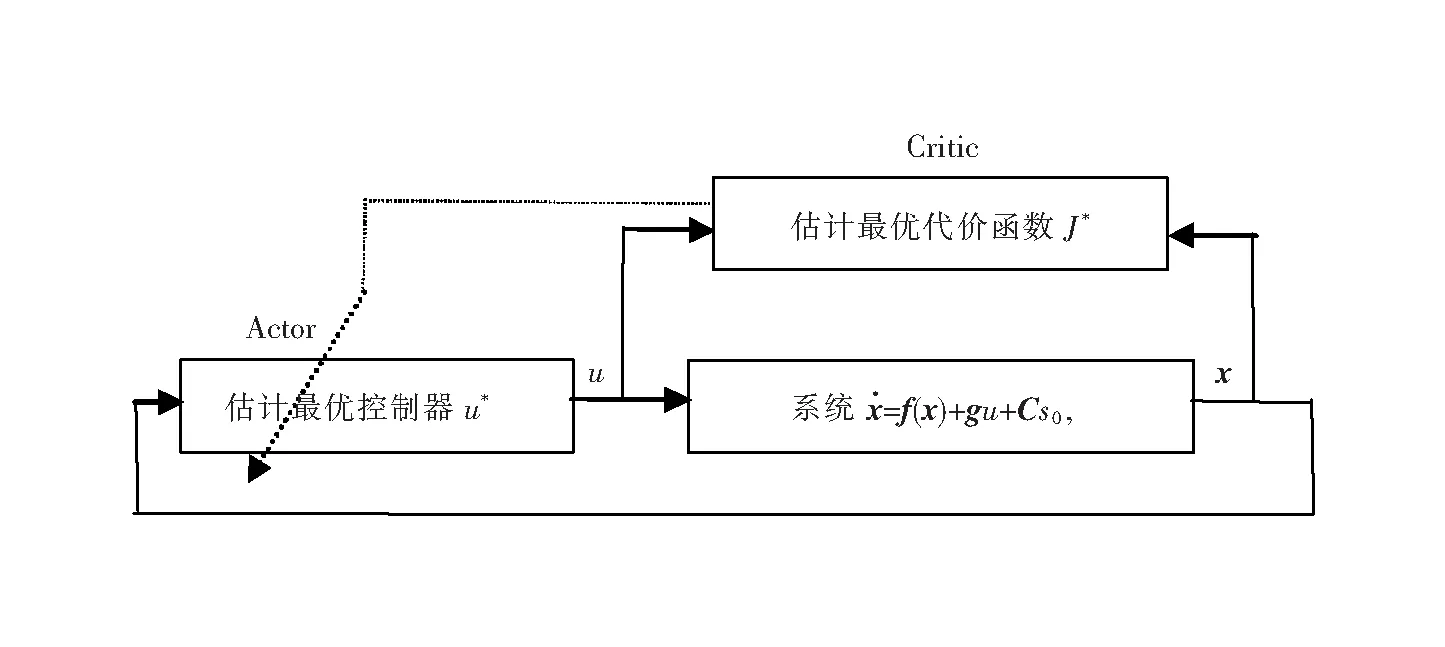
图2 A-C算法结构
(1) Critic设计
用
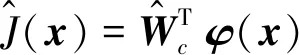
(15)
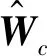
(16)
作为H*的估计。注意到H*=0,考虑如下函数
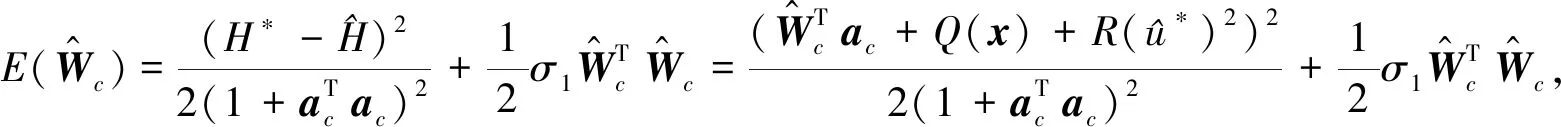
(17)

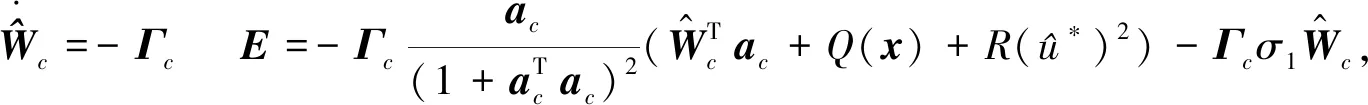
(18)
其中Γc>0是一个正定矩阵。系数σ1在自适应律(18)中作为泄漏项出现。
(2)Actor设计
用
(19)
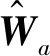
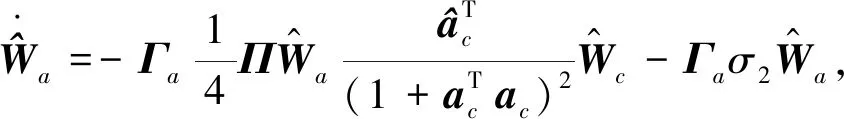
(20)
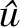
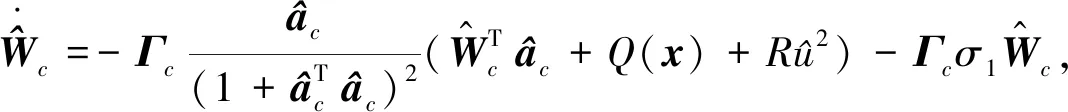
(21)
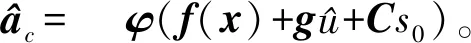
注2不同于文献[18-20]中的算法,为了提高系统的鲁棒性,在Actor-Critic更新率中增加了泄漏项(见式(18)和式(20)的最后一项)。
将式(19)代入式(2)得闭环系统为
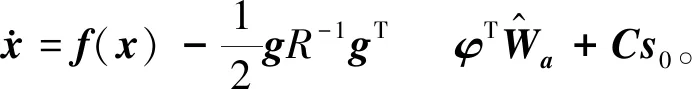
(22)
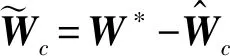
(23)
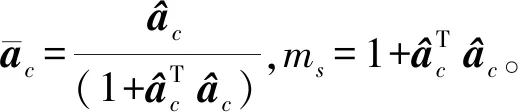
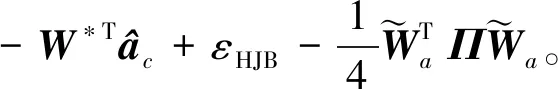
(24)
3 稳定性分析
为了便于稳定性分析,需对神经网络逼近作如下假设。
假设2(1)W*有界,即存在一个常数ω>0,使得‖W*‖≤ω;



由式(8),(11)和(13)知HJB的估计误差可表示为如下形式:

(25)
文献[17]指出,随着N的增加,εHJB均匀收敛于零。则对于固定的N,εHJB是有界的,即存在常数εmax>0,使得‖εHJB‖≤εmax,并且εmax会随着N的增加而减少。

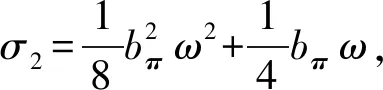

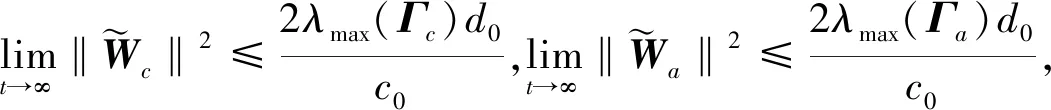
(26)
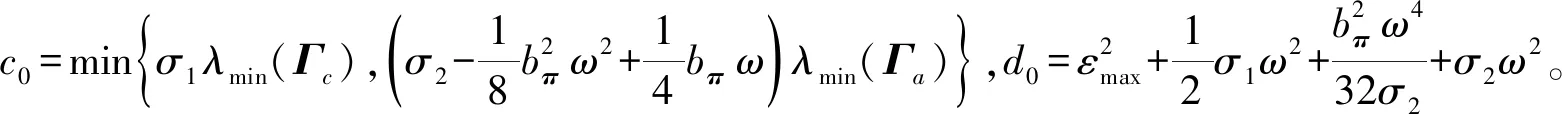
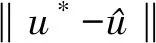
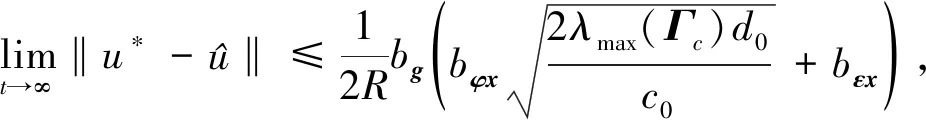
(27)

(3)存在一个紧集Ω,当初始状态x(t0)∈Ω时,闭环系统(22)中的状态x一致终极有界,从而主动悬架的状态s1和s2局部一致终极有界,且终极边界可通过调节参数充分小。
证明考虑李雅普诺夫函数

(28)
由式(23)知V的导数满足
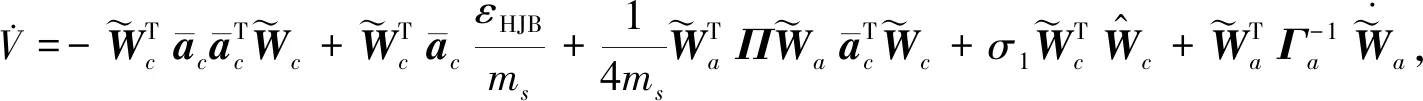
(29)
(30)
将式(23)和(30)代入式(29)得
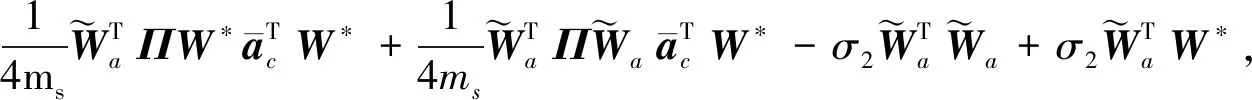
(31)
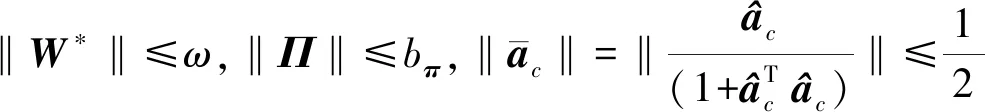
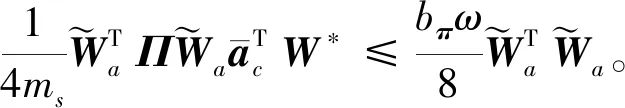
(32)
由假设2和Young不等式知
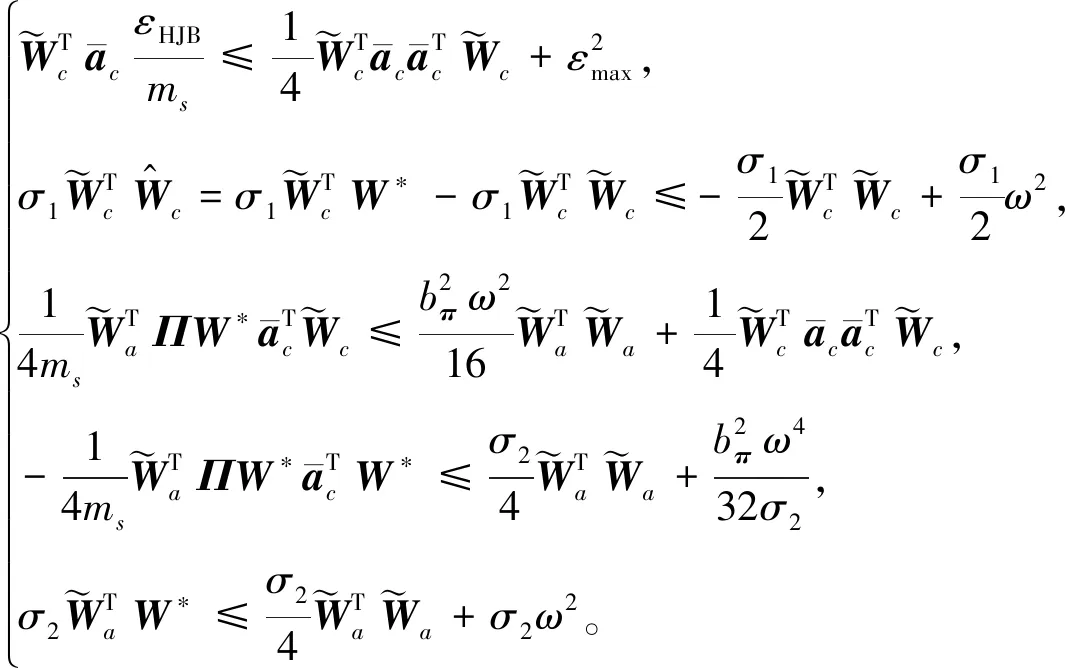
(33)
将式(32)和(33)代入式(31)得
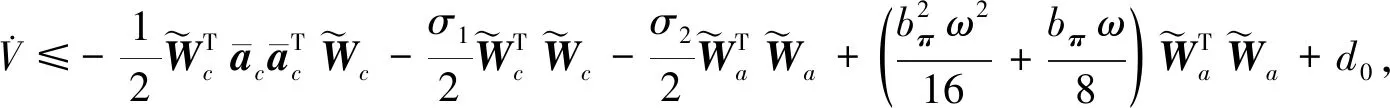
(34)
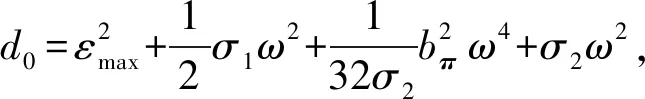
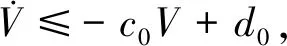
(35)
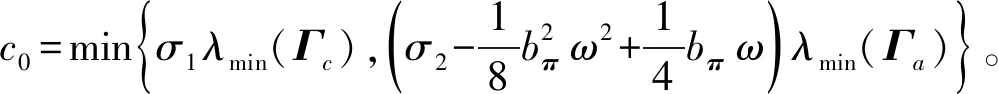
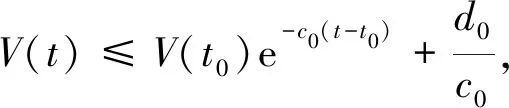
(36)
再结合式(28)可得
(37)
这使得式(26)成立。
由式(12),(19),(37)和假设2知
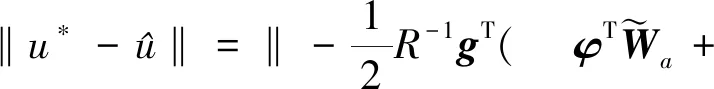
(38)
这使得式(27)成立。
由J*(x)的定义知其是正定且径向无界的,则由文献[24]中的引理4.3知,存在K∞类函数α1和α2,使得
α1(‖x‖)≤J*(x)≤α2(‖x‖)。
(39)
由式(10),(14)和(22)知J*(x)的导数满足
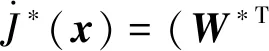
(40)
由Q(x)的定义知
Q(x)≥q‖x‖2,
(41)
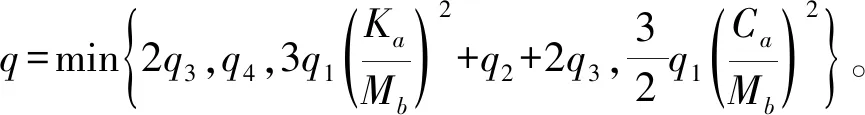
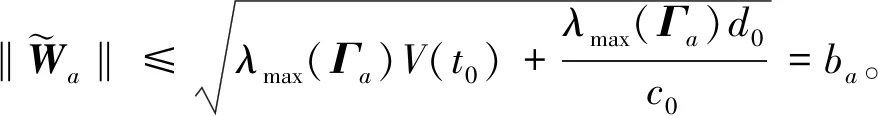
(42)
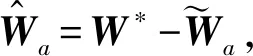
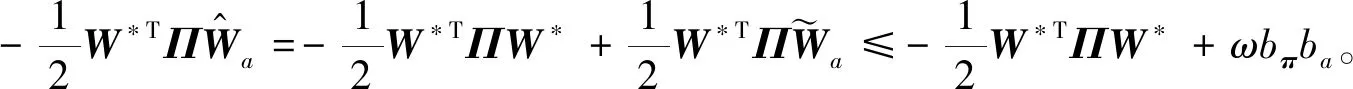
(43)
在紧集ΩM上,由式(3)和假设1,2可知

(44)
将式(41),(43)和(44)带入式(40)可得
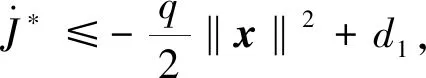
(45)
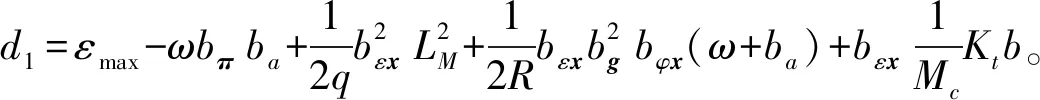
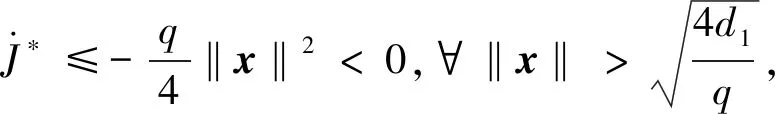
(46)
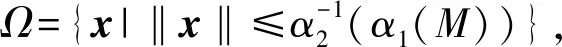
4 结 论
本文考虑了在崎岖路面上的1/4汽车非线性主动悬架系统的最优控制问题。综合考虑车身加速度, 悬架扰动度和轮胎的位移等因素给出了合理的代价函数,提出了一种新颖的基于强化学习的在线Actor-Critic迭代算法的最优控制策略,同时增加泄漏项提高系统的鲁棒性。所提策略使得主动悬架系统的位移终极有界,同时使代价函数达到最优。
另外,为保证汽车舒适度和行驶的安全度,还需综合考虑优化、安全和控制问题,并将结果应用到1/2悬架和全车悬架系统中。

