带有Hardy-Sobolev临界指数的 椭圆型方程解的存在性
杨 帆,王琳琳
(鲁东大学数学与统计科学学院,山东 烟台 264039)
本文将研究带有Hardy项和Hardy-Sobolev临界指数项的奇异型椭圆型方程
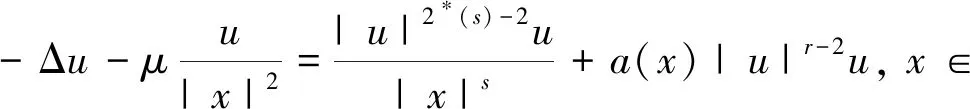
(1)
(A)a(x)在N{0}上非负局部有界,在以原点为中心的有界邻域G中a(x)=O(|x|-m),当|x|→∞时,a(x)=O(|x|-t),0≤m 方程(1)对应的能量泛函为 (2) 椭圆型方程在流体力学、弹性力学和几何学中都有重要作用。大多数学者研究在有界域且带有Hardy项和Hardy-Sobolev临界指数项的椭圆型方程[3-6]: (3) 其中Ω是N(N≥3)中一个有界的开子集,0≤s<2,2*(s):=2(N-s)/(N-2)是Hardy-Sobolev临界指数,当λ1在一定范围内,f1(x,u)满足一些条件时,研究方程(3)解的存在性。文献[7]证明了带有Hardy项和Sobolev临界指数项的奇异型椭圆型方程: (4) 其中Ω是N(N≥3)中一个有界的开子集,λ2在一定范围内,满足一些条件时,方程(4)有多个非平凡解。在全空间上带有Hardy项,Sobolev临界指数项或Hardy-Sobolev临界指数项的椭圆型方程的研究也取得一些成果[8-12]。在全空间上带有Hardy项和Sobolev临界指数项的奇异型椭圆型方程有解的结论[2],那么在全空间上带有Hardy项和Hardy-Sobolev临界指数项的奇异型椭圆型是否有解?通过运用Hardy不等式,Hardy-Sobolev不等式以及山路引理证明了方程(1)有非平凡解。主要结果如下: 定理1假设a(x)满足条件(A)且 则方程(1)至少有一个解。 本文出现的Ci(i=1,2,3,…)表示不同的大于零的常数。 引理1(Hardy不等式)[1]设1 特别地,当p=2时,该不等式为 引理3 (山路引理)[13]设E是Banach空间,能量泛函J∈C1(E,),J(0)=0,满足条件: (i)存在γ,ρ>0,使得当u∈Sγ={u∈E:‖u‖=γ}时,J(u)≥ρ。 (ii)存在e∈E,使得当‖e‖>γ时,J(e)≤0。 的解,且满足 其中As为最佳常数, 当R<|x|<2R时,0≤φ(x)≤1。 ‖vε‖2=As+O(ε(N-2)/(2-s))。 (5) 引理5 若a(x)满足条件(A)且 则ε→0+时, 证明设ωN表示N维单位球体的表面积,当1≤q<2*(m)时, 分类讨论: 即 (6) (7) 由式(7)得, (8) (9) 由条件(A),式(8)和式(9)得, (10) 当ε→0+时,由式(5),式(6)和式(10)得, (11) 由式(5)和式(11)得, 因此,结论得证。 证明由J(un)→c,J′(un)→0,得J(un)=c+o(1),〈J′(un),un〉=o(1)‖un‖, o(1)+o(1)‖un‖+2c= 2J(un)-〈J′(un),un〉= 由 o(1)+o(1)‖un‖+C8, 令vn=un-u,由文献[15]的Brezis-Lieb引理得 ‖un‖2=‖vn‖2+‖u‖2+o(1)。 (12) 由 〈J′(u),u〉+‖vn‖2+o(1)=‖vn‖2+o(1), 因此,结论得证。 本文是文献[2]的推广,文献[2]通过运用Hardy不等式和分析技巧得到所需要的条件,运用Brezis-Lieb引理和反证法证明(PS)c序列强收敛,最后运用山路引理证明非平凡解的存在性。本文中s的限制条件为0≤s<2,当s=0时,方程(1)非平凡解的存在性即为文献[2]所研究的内容,本文还运用Hardy-Sobolev不等式,证明(PS)c序列强收敛并没有运用反证法。下一步工作是研究方程(1)非负解以及多解的存在性。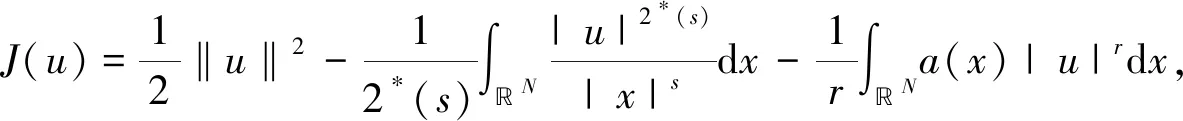
1 准备工作
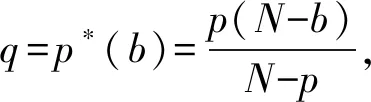
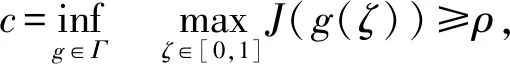
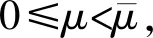
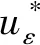
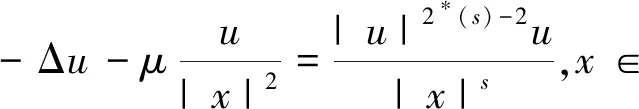
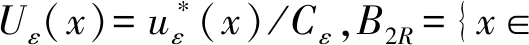
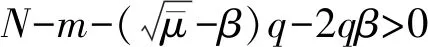
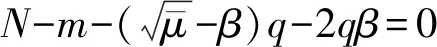

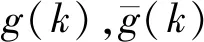


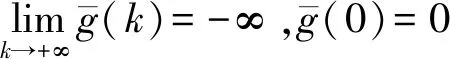
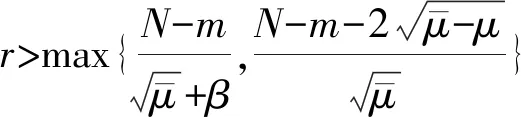
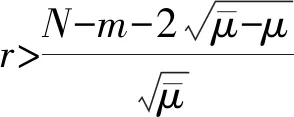
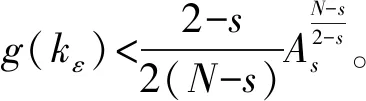
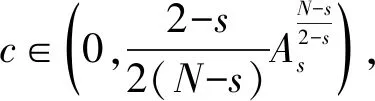
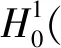

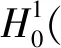
2 定理1证明
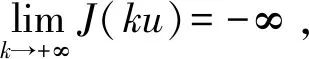
3 结 论

