基于弹簧刚度法的螺栓分布研究

聂星月，施雷，王健刚，冯定，邵雪，杨江怀

(1.长江大学机械工程学院，湖北荆州 434023；2.中石化机械工程公司第四机械厂，湖北荆州 434024)

0 前言

与常规螺栓连接不同的是，铰制孔螺栓连接是采用过盈配合连接两个零部件的一种连接方式。由于铰制孔螺栓与被连接件之间紧密配合，因此可以承受较大的剪切作用。在重载设备的紧固连接中，通常采用多铰制孔螺栓连接来承受较大的径向载荷。螺栓的分布问题是多铰制孔螺栓连接载荷分布均匀与否的关键。因螺栓分布不均而导致的振动与螺栓损坏问题屡见不鲜[1-3]。但在现有的螺栓组设计技术资料中，并未对铰制孔螺栓的分布提出明确的要求[4-6]。

目前，国内外研究学者针对螺栓的数量、尺寸、被连接件的材料、刚度等问题对多螺栓分布进行了研究。NOROOZI等[7]对单轴加载条件下单排和交错排两种不同螺栓分布情况进行了试验研究和比较，发现螺栓分布方式对承载能力和失效形式有显著影响。KIYOKAWA等[8]对螺栓的间距进行了实验研究，结果表明螺栓间距减小会导致螺栓极限强度降低。KONKONG、PHUVORAVAN[9]建立了多螺栓连接的弹簧模型，研究了不同螺栓直径、板厚和板厚比对螺栓载荷分布的影响。XIANG等[10]考虑了孔隙和摩擦效应，改进了现有的理论刚度方法，该方法缩短了建模时间，对载荷预测具有更好的时效性。LIU等[11-13]提出了改进的三级弹簧法，在考虑螺栓孔拉伸变形的基础上，提出了孔变形对应的附加刚度概念及计算方法，研究了复合材料多螺栓节点载荷的分布规律，结果表明：改进的方法对多螺栓节点载荷的分布具有更高的预测精度。

通过对上述文献的研究发现，目前常采用弹簧刚度法对多螺栓的载荷分布进行预测。该方法将连接件与被连接件简化为矩形板，然后用单一的刚度计算方法计算其刚度。但用多螺栓连接复杂的零部件时，没有针对复杂的结构提出刚度计算方法。在井架、起重机等复杂结构中，多螺栓连接不仅仅依靠矩形板提供刚度，还需考虑其复杂的桁架结构。在重载条件下进行简单的简化会导致分析结果与实际情况产生较大的差异。因此，本文作者在原有刚度法的基础之上，针对复杂的结构，提出了一种桁架结构刚度的计算方法，用于研究多螺栓载荷分布的预测。

1 螺栓载荷分布计算方法

1.1 多螺栓连接模型

在齿轮齿条钻机中，通常采用多铰制孔螺栓连接齿条与井架。钻机井架是断面形状为“K”形、截面为П形的空间桁架结构。井架大腿、人字架等主要受力件采用H形钢制造[14]。该特殊结构使井架拥有足够的强度、刚度和整体稳定性。常规的刚度计算方法仅将连接件简化为矩形板，考虑板宽和板厚对刚度的影响，并未研究其复杂的空间桁架结构对刚度的影响。

以六螺栓连接的重载齿轮齿条钻机为例，采用整体弹簧刚度法建立钻机齿条-螺栓-井架系统动力学模型。在简化过程中，按照质心不变的原则，将齿条和井架均离散为采用N段无质量的弹簧连接的集中质量。图1为铰制孔螺栓连接齿条时载荷分布的弹簧模型。图中所示的特殊模型是用于六螺栓连接的，但可以针对任意数量的铰制孔螺栓进行修改。如图2所示，其中上板(齿条)称为拼接板，下板(井架)称为外板。拼接板的厚度和材料可以与外板的厚度和材料不同，每个螺栓可以有不同的直径和材料。

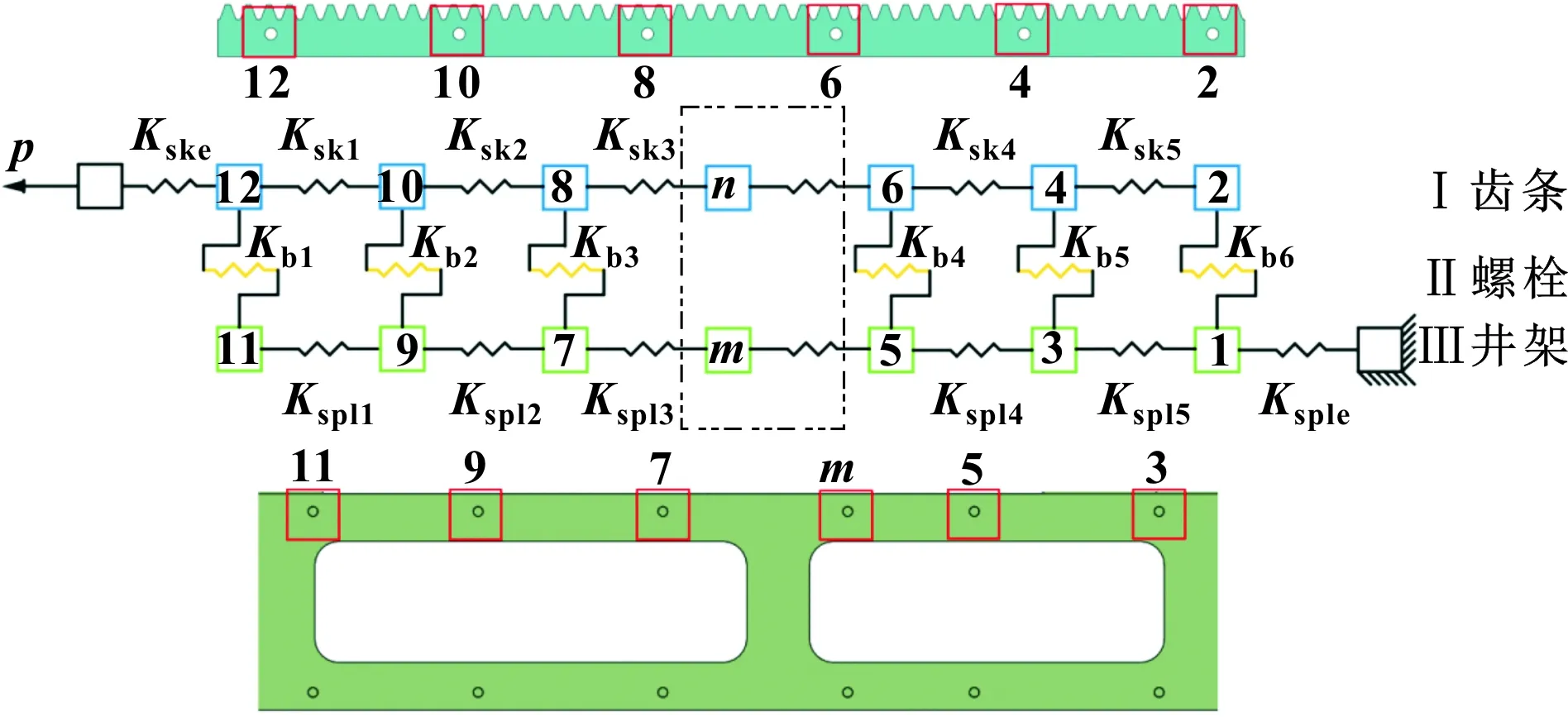
图1 六螺栓连接的弹簧单元模型

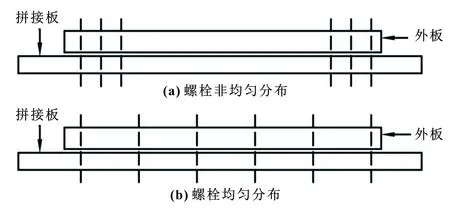
图2 螺栓连接的两种模型

1.2 螺栓受力分析

Kb1、Kb2、Kb3、Kb4、Kb5、Kb6表示螺栓刚度；Ksk1表示螺栓1～2之间齿条的等效刚度，Ksk2表示螺栓2～3之间齿条的等效刚度，Ksk3表示螺栓3～4之间齿条的等效刚度，Ksk4表示螺栓4～5之间齿条的等效刚度，Ksk5表示螺栓5～6之间齿条的等效刚度；Kspl1、Kspl2、Kspl3、Kspl4、Kspl5与上述类似，表示井架之间的等效刚度；Ksple表示螺栓6与井架自由长度末端之间的井架等效刚度；Kske表示螺栓1与齿条自由长度另一端之间的齿条等效刚度。

关于图1中的模型，应注意以下几点：

(1)模型只能在水平方向上自由移动。

(2)所有的弹簧(包括螺栓弹簧)只有水平方向的刚度。

假设摩擦效应可以忽略不计。

如图1所示，图中所有弹簧的刚度均已知，可直接确定给定载荷下每个质量的位移，可以确定模型中每个元件的受力图。例如，图3中显示了井架1号件和齿条4号件的受力分析图，以及其运动方程。

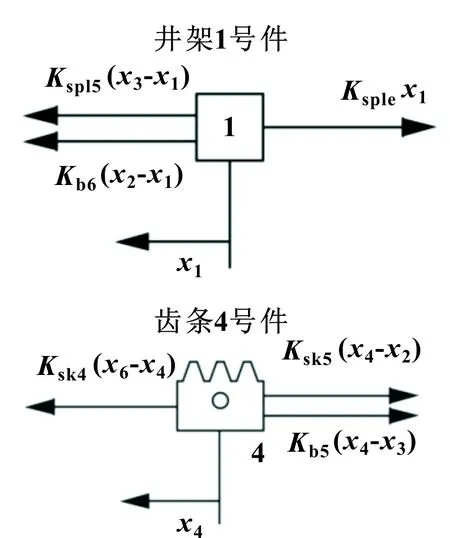
图3 井架和齿条的受力图

井架1号件的运动方程为

(1)

齿条4号件的运动方程为

(2)

则可得到如下形式的线性方程组：

(3)

对于准静态加载，加速度可以忽略，得到如下方程：

(4)

式中：A1=Ksple+Ksp5+Kb6；A2=Kb6+Ksk5；A3=Ksple+Kspl4+Kb5；A4=Kb5+Ksk5+Ksk4；A5=Kspl3+Kspl4+Kb4；A6=Ksk3+Ksk4+Kb4；A7=Kspl3+Kspl2+Kb3；A8=Ksk3+Ksk2+Kb3；A9=Kspl2+Kspl1+Kb2；A10=Ksk2+Ksk1+Kb2；A11=Kspl1+Kb1；A12=Ksk1+Kske+Kb1。

通过载荷向量P与刚度矩阵K的逆相乘，可以计算出每个质量的位移。

联立各节点的运动方程，可得到基于弹簧刚度法的六螺栓平衡方程矩阵。

KX=F

(5)

整体位移

X=[x1x2x3x4x5x6x7x8x9x10x11x12x13]T

(6)

以螺栓1为例，计算齿轮齿条钻机工作时，连接齿条与井架的铰制孔螺栓所受的剪切应力：

F1=Kb1(x12-x11)

(7)

(8)

式中：x11为质量11的位移；x12为质量12的位移；F1为螺栓1所受的力；τ1为螺栓所受的剪切应力。

单个螺栓的预紧力P1：

(9)

式中：σs为螺栓的屈服应力；d1为外螺纹中径；d2为外螺纹计算直径(d2=d3-H/6，即计算直径为螺纹小径的基本尺寸d3减去螺纹原始三角形高度H的1/6值)。

1.3 弹簧刚度的计算

步骤1，齿条刚度。

齿条的等效刚度是直接计算的。以螺栓1和2之间的刚度为例：

(10)

式中：Esk为齿条在纵向或加载方向的弹性模量；wsk和tsk分别为齿条的宽度和厚度；p为螺栓之间的间距；d为螺栓的直径。Ksk2、Ksk3、Ksk4、Ksk5和Kske也使用类似的表达式。

步骤 2，螺栓刚度。

对螺栓刚度的计算，NELSON等提出了以下单搭接螺栓刚度的修正方程[15]：

(11)

式中：下标b、spl、sk分别表示螺栓、外板、拼接板；t表示厚度；E、G分别为弹性模量和剪切模量；Ab表示螺栓的横截面积；EL、ET分别表示横向与纵向的弹性模量；系数β表示连接件上承受应力所产生的螺栓弯矩百分数。当β=0.15时，与实验的载荷-应力曲线有很好的一致性。

步骤 3，井架刚度。

图4(a)为桁架结构横截面的简化模型，所示的特殊模型适用于四面封闭的板条结构，但它可修改为任意数量板条的叠加。图4(b)为其简化的计算模型，将板条两端固定，任意一点处扰度可简化为正交板条扰度的叠加。假设正交板条宽度分别为B1、B2，依据材料力学的扰度叠加法，可计算出任意载荷作用下桁架结构的变形量。

对于单位长度的两端固定单板条，提出了以下的刚度计算公式：

(12)

式中：E为板条的弹性模量；h′为板条高度；l为板条长度；B为板条宽度。

由此可用叠加法计算出任意桁架结构的刚度，板条的长、宽、高以及放置角度均可更改。以图4(a)所示的四面封闭的板条为例，其单位长度的刚度计算方程为

(13)

图4 井架应力分析

以螺栓1与螺栓2之间的井架刚度为例：

(14)

h=kh′

(15)

式中：E为井架的弹性模量；l1、l2为井架截面的长度[如图4(d)所示]；B1、B2为井架截面的宽度[如图4(e)所示]；h′为井架的实际高度；h为井架的等效高度。Kspl2、Kspl3、Kspl4、Kspl5和Ksple也使用类似的表达式。其中k为等效高度系数，该系数表示单位长度的桁架在外力作用下，受力方向的变形量之比，该系数可采用整体有限元法进行计算，也可以通过实验求得。

2 试验部分

2.1 试验材料

基于齿轮齿条钻机的对称式提升箱，考虑部分齿轮失效的特殊情况(单根齿条仅一个齿轮正常工作)，依据其结构形式及工作原理，重点研究了铰制孔螺栓在不同分布下，螺栓所受剪切应力的情况。为降低计算复杂度，忽略齿轮与螺纹细节，建立了两种齿条固定在井架连接板的几何模型，如图5所示。

图5 井架和齿条的几何模型

(1)螺栓布置方式是均匀分布，取螺栓间距为a，左端第一个螺栓孔形心与齿条左端距离为p1。

(2)螺栓布置方式是两侧螺栓对称分布，同一侧取螺栓间距为b，左端第一个螺栓孔形心与齿条左端距离为p2。

进行试验的钻机名义钻井深度为4 000 m，钻机最大钩载为 2 500 kN，提升装置可施加的最大下压力为 625 kN。根据该钻机的设计要求，对其进行了相关分析，最终确定钻机提升装置中的齿轮材料采用 20CrMnTi，齿条材料采用 40CrNi2Mo，两种材料具体的属性参数如表1所示。同时对齿轮和齿条的表面进行淬火和调质处理。

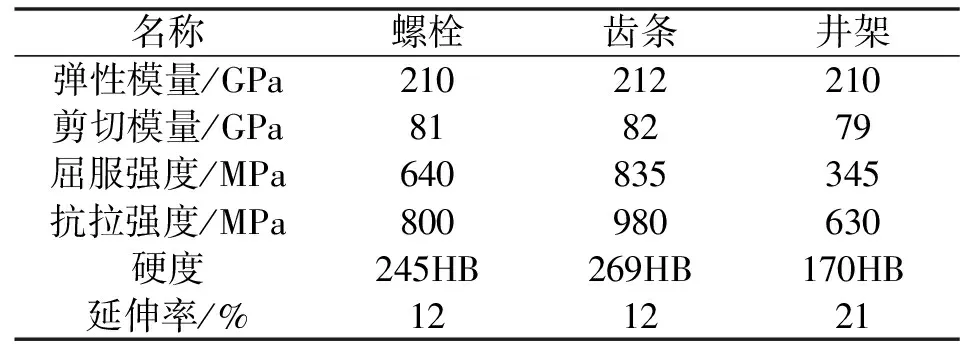
表1 材料的机械性能

研究的齿轮齿条钻机，运行速度低，承受载荷大。为减小钻机整体结构，同时满足工厂齿轮加工能力，在齿轮齿条传动系统的设计中，齿轮采用了标准渐开线直齿轮，具体设计参数如表2所示。

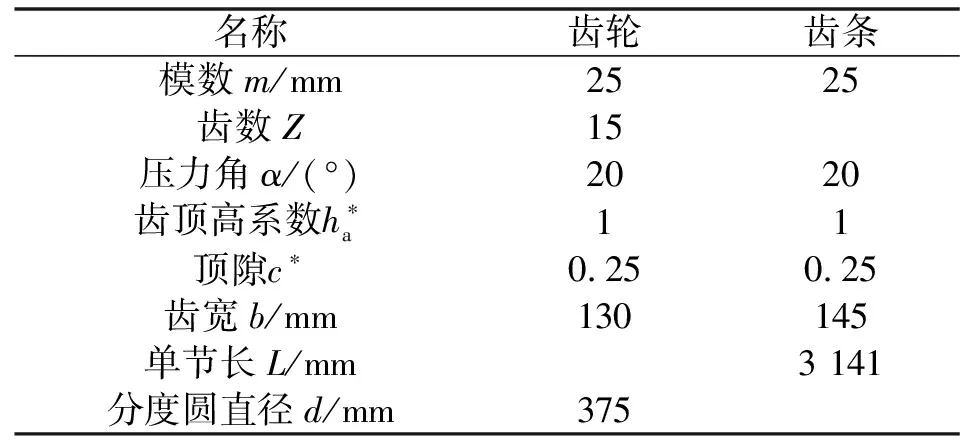
表2 齿轮和齿条基本参数

分别在齿条上6个不同位置加载，用以模拟齿轮齿条在不同位置啮合。所有试件的几何形状如图6所示，图中还显示了此处使用的螺栓编号。所有试验均采用铰制孔螺栓，添加扭矩为39 kN·m。

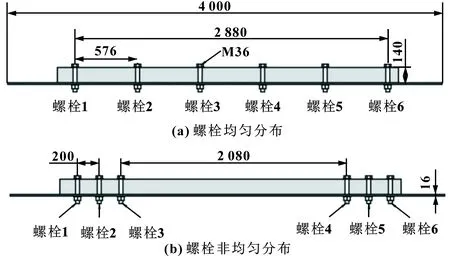
图6 带有螺栓编号的井架连接试件几何形状

2.2 试验方法

试验是基于自主搭建的齿轮齿条钻机提升实验装置进行的。该实验装置由机械系统、控制加载系统、信号采集处理系统几部分组成。为了测量载荷分布，每个螺栓外部(齿条)安装了应变片，如图7所示。结合现场实际情况，试验最终选择了BE120-4AA单轴应变片，该应变片为胶基箔式应变片，电阻值较小，受外界干扰较少，适合室外试验。每个测点需要2个应变片，分别与齿条节线成0°和90°，其中成90°的应变片在另一应变片上方。

将每个测点上的应变片依次与桥盒(1/4 桥接法)、静态应变仪、数据采集器、计算机相连，并通过测试软件进行灵敏度和工作方式的设置，通过调整应变仪使其处于平衡位置。在正式试验加载前，需先进行预加载，反复加载钩载 2～3 次，载荷负荷值不超过2×105N，观察试验装置和仪器是否正常工作，如果表现正常，则测试已经处于最佳状态，可以开始测试。

此次试验的齿轮齿条啮合点有6个，啮合点分别位于两相邻螺栓之间以及第一个螺栓上方。通过控制油缸压力来模拟钻杆负载，进行最大设计载荷作用下螺栓剪切应力的测试。通过释放齿轮离合器模拟可能出现的齿轮失效工况。试验采用等增量法加载，分别记录齿轮齿条在不同啮合点时齿条的静态应变状态。采集时间设置为10 s。重复此步骤3次，即每组载荷记录3次应变值，以确保试验结果的准确性。试验装置如图7所示。

由于螺栓张力在最初的24 h内大约发生90%的下降，为了考虑螺栓松弛的影响，在装配后一周进行了测试。螺栓的应变和螺栓的剪切应力两者呈线性相关。利用这种相关性，可以确定螺栓的剪切应力。

图7 螺栓剪应力测量试验

2.3 试验结果

试验完成后，对试验采集的数据进行记录与分析，考虑到使用仪器、设备会受到精度制约，以及所采用的测试办法存在缺陷，甚至试验时会受到环境条件的影响和人为因素的约束，所以试验得到的应变值存在一定的误差，故必须对所测得的数据进行适当的分析和进一步的处理，以减少误差得到反映实际试验规律的物理量。

表3与表4记录了螺栓在均匀分布与非均匀分布时，齿条上螺栓孔横向与纵向的微应变ε。

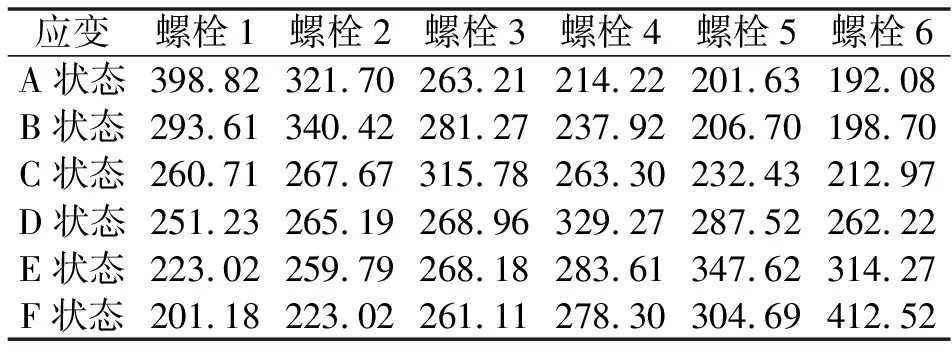
表3 螺栓均匀分布时的应变ε 单位：10-6

表4 螺栓非均匀分布时的应变ε 单位：10-6

由于表中记录的应变数据为微应变，根据广义胡克定律可知空间应力状态下应力与应变之间的关系：

σ=εE

(16)

则可以计算处各个应变片方向的正应力。为了使分析更加直观，根据上述表格绘制了螺栓的剪切应力，如图8和图9所示。

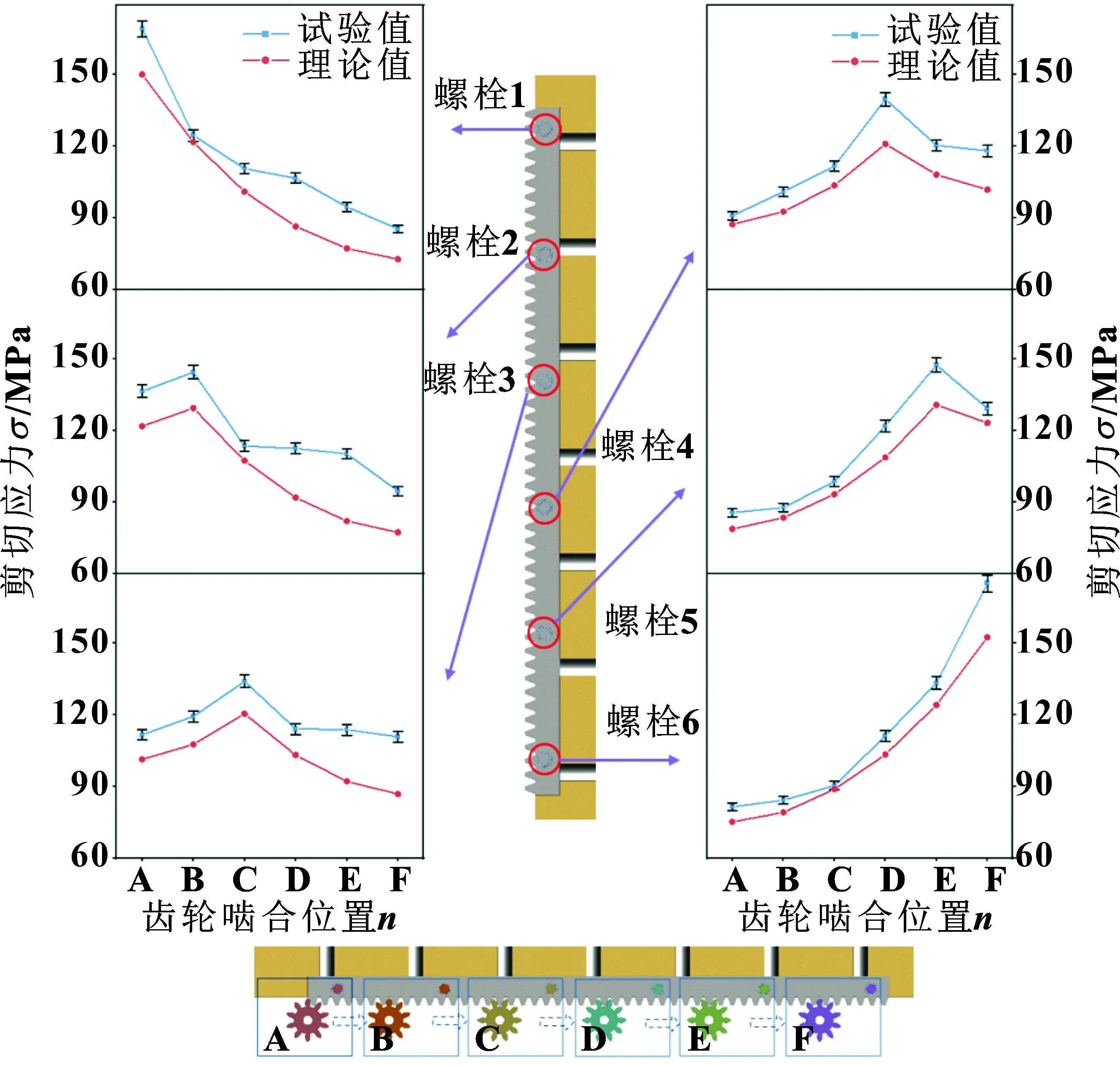
图8 螺栓分布均匀时螺栓的剪应力

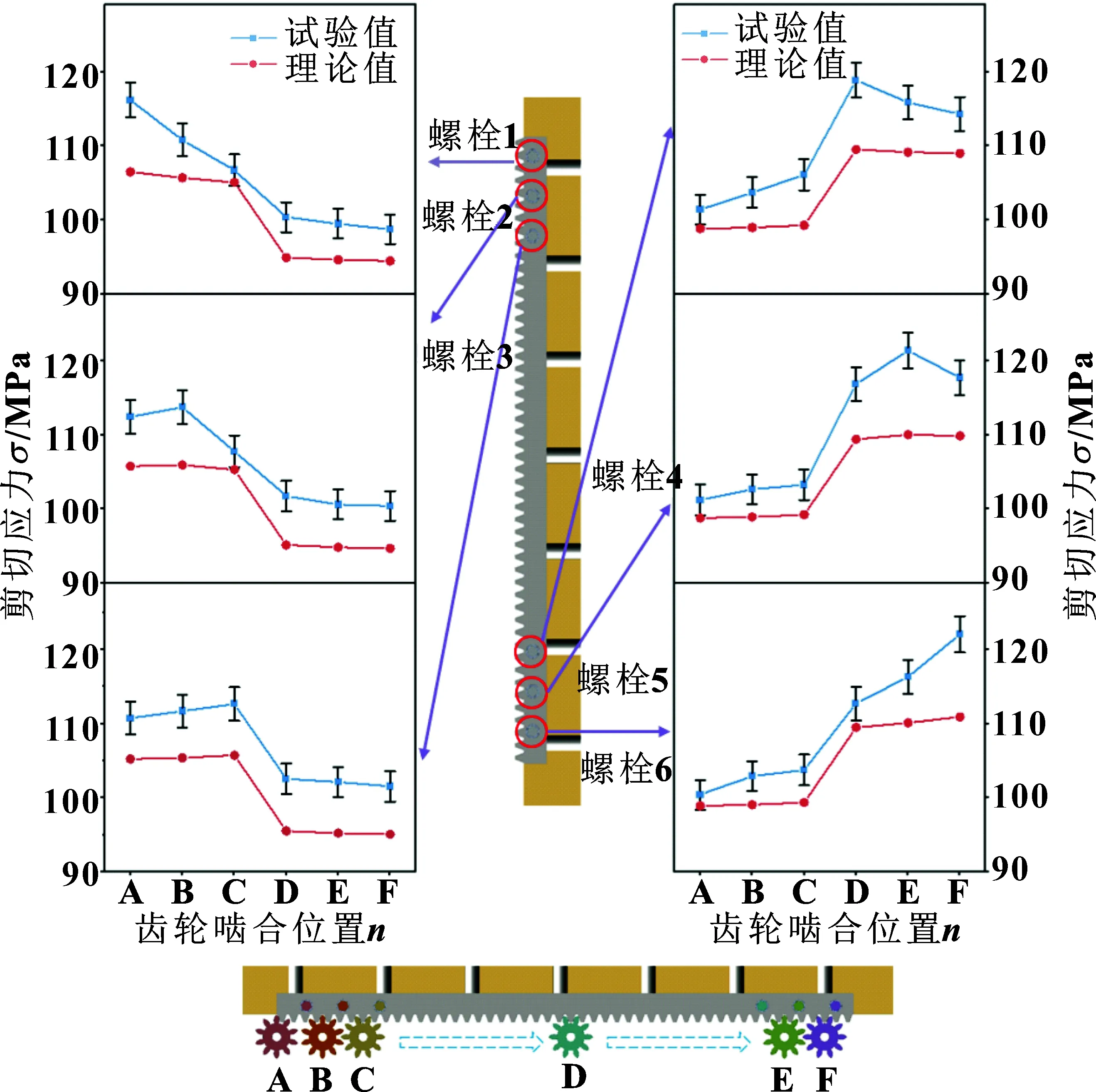
图9 螺栓非均匀分布时螺栓的剪切应力

试验结果表明：当其中一个螺栓距离载荷位置最近时，该螺栓所受的剪切应力相较于其他5个螺栓更大。两侧对称分布的螺栓连接中，端部螺栓承受的载荷波动大于更靠近中间螺栓的载荷。3号和4号螺栓位置关于单节齿条的几何中心对称分布，螺栓载荷幅度最为均衡。随着载荷位置向下移动，1-6号螺栓的剪切应力的平均值逐渐增大，研究认为齿条下端螺栓不仅承受传动系统传递的载荷，同时还需要承受齿条以及系统的自重载荷。当螺栓均匀分布时，螺栓的应力方差大于非均匀分布时螺栓的应力方差，研究认为，螺栓非均匀分布条件下，螺栓组载荷分布更均匀。在材料力学性能恒定的情况下，齿条与螺栓的刚度不同，在承受相同载荷时，两者产生的弹性形变也存在差异。

3 有限元分析

3.1 模型基本假设

试验结果表明，螺栓的分布方式对螺栓所受剪切应力会产生影响。为了更详细地阐明它们的影响，采用简单的模型进行有限元分析。

基于所设计的井架结构，采用铰制孔螺栓连接。当被连接件间有相对滑动时，依靠螺栓本身的抗剪作用，防止其运动。其力学模型为一个高度非线性接触问题。其三维有限元模型网格单元通常高达百万个单元，数量巨大，因此需要简化模型以减少运算。采用有限元软件对铰制孔螺栓进行模拟分析，对铰制孔螺栓连接的模型做如下假设[16]：(1)螺栓材料为各向同性材料；(2)忽略钻机上其他装置对螺栓应力的影响。

3.2 模型网格

在此研究中，作者建立了一个多螺栓连接的有限元模型，并分别对每个螺栓施加相同的载荷，计算各个螺栓的剪切应力。以铰制孔螺栓为研究目标，考虑井架结构和载荷关于中间截面对称的特点，建立多螺栓连接的有限元模型(只选取对称轴的一侧)。为了更好地考虑三维方向上载荷位置、接触与结构刚度对铰制孔螺栓剪应力的影响，旨在使用有限元软件对考虑载荷位置的齿条多螺栓紧固模型进行有限元方法类分析设计。为了提高计算精度，对齿条螺栓孔附近采取了局部加密的方式。如图10所示，网格划分时采用六边形八节点单元，生成网格的雅克比均大于0.7。以在齿条上均匀分布的螺栓为例，绘制其三维有限元模型，其模型网格单元为150万。其中螺栓与齿条的接触、齿条与井架连接板的接触、螺母与连接板的切向接触被定义为摩擦接触，摩擦因数分别设为0.2、0.4、0.2，并对螺栓施加39 kN的预紧力。

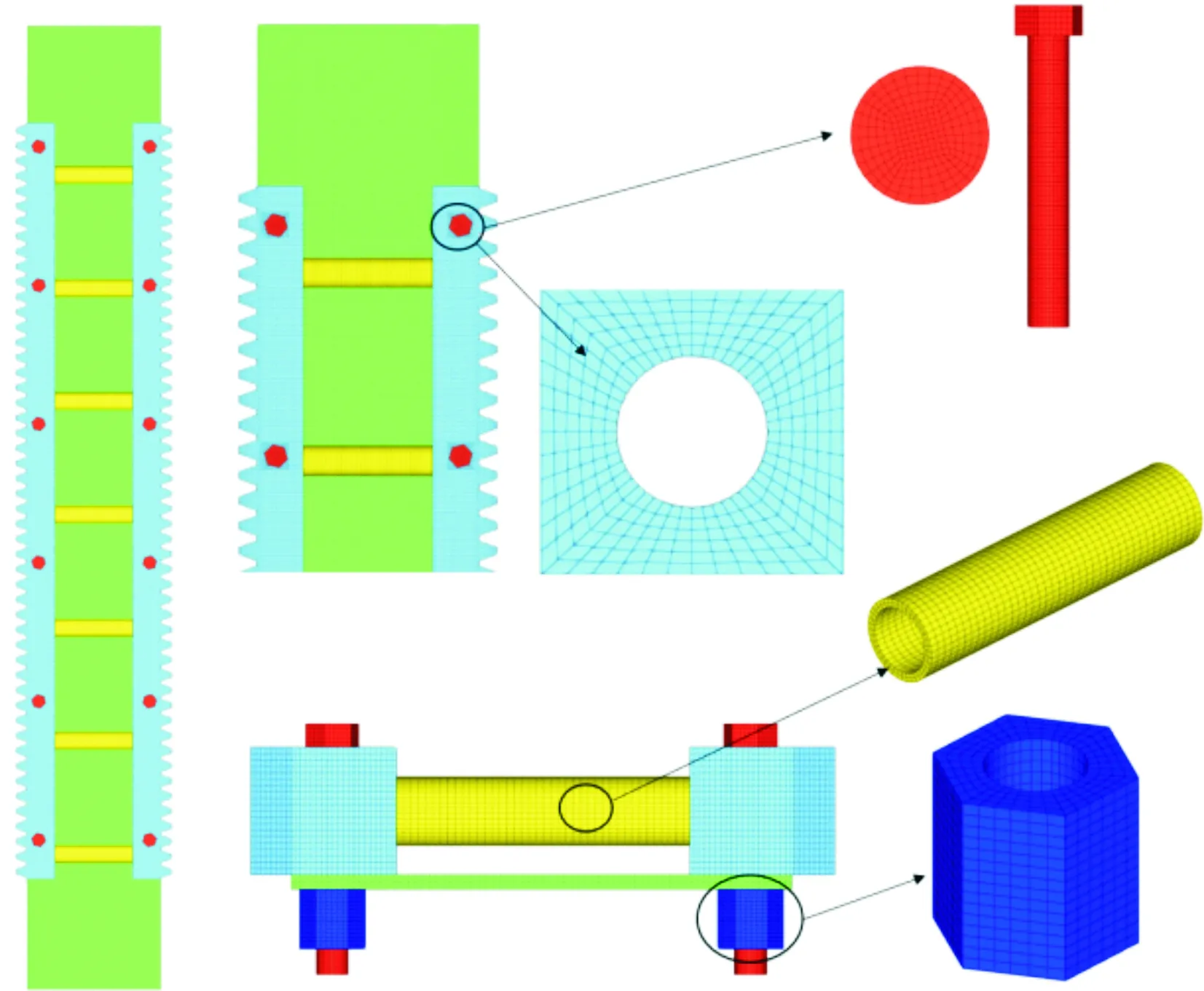
图10 铰孔螺栓连接的三维有限元模型网格划分

3.3 有限元计算结果

为研究齿轮齿条传动过程中载荷位置对螺栓承载情况的影响，选取齿轮在齿条上的6个啮合齿进行分析。通过计算螺栓所受剪切应力的大小作为评估螺栓紧固效果指标。根据结构对称特点，仅需对一根齿条上的应变情况进行研究。

依据上文可知，在齿轮齿条啮合传动的过程中，啮合位置下端最近的螺栓剪切应力最大。为了研究螺栓在不同分布情况下，螺栓所受的最大剪切应力，分别在第一个螺栓上方及两螺栓之间施加载荷，以模拟齿轮齿条钻机的动态工况，然后对啮合位置下端最近的螺栓进行有限元分析。图10与图11显示了螺栓在不同分布情况下所受的最大剪切应力情况。即使被连接件之间的摩擦力将横向载荷抵消，螺栓最大剪切应力在不同分布位置下依旧发生了显著的变化，证实了螺栓分布情况对螺栓最大剪切应力的影响明显。且三维有限元法考虑了螺栓Z方向的载荷、接触和结构刚度等因素，能够很好地验证铰制孔螺栓所受剪切应力情况。

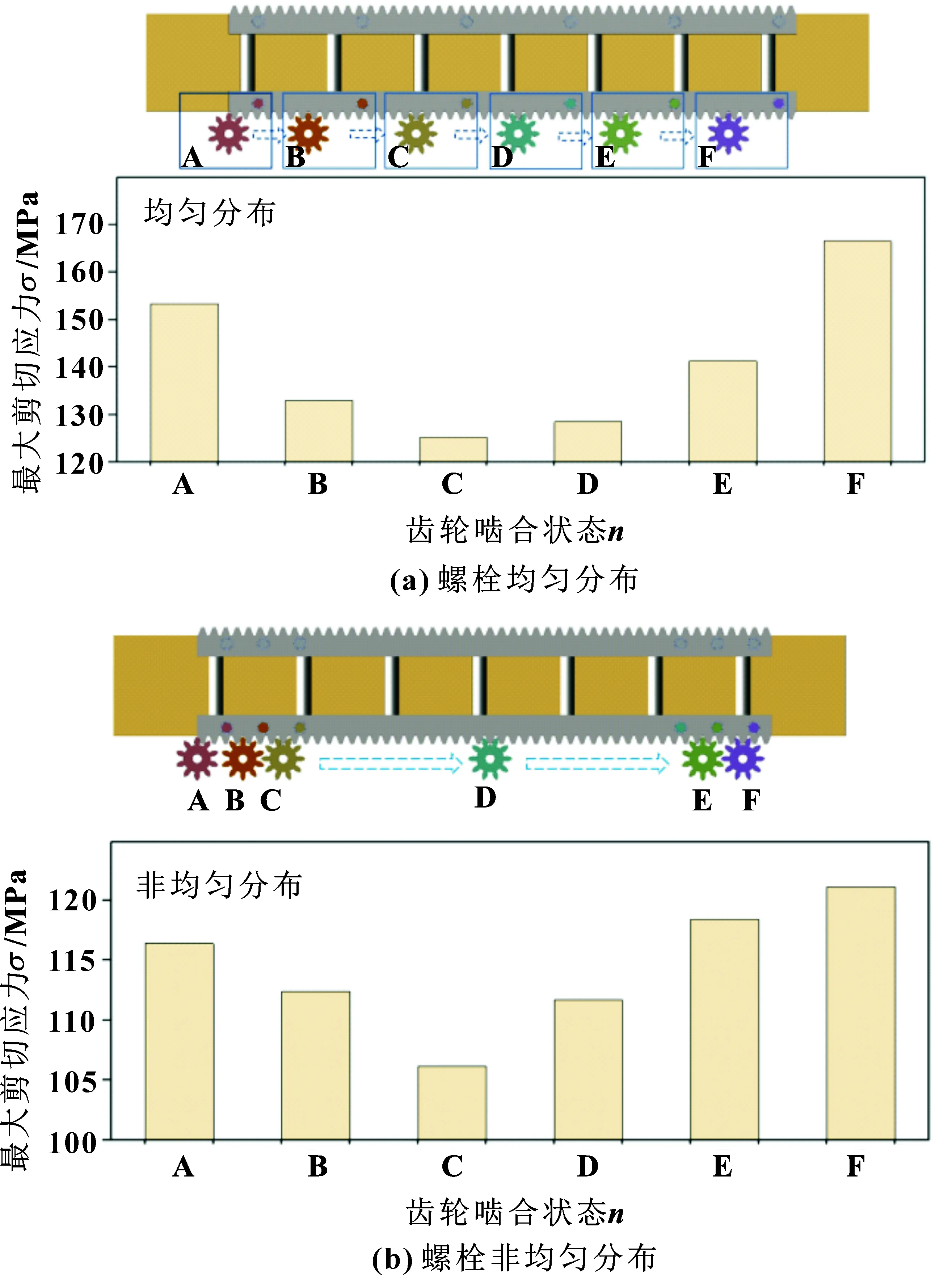
图11 不同螺栓分布情况下的螺栓最大剪应力

从图11可以看出：当螺栓均匀分布时，螺栓所受的最大剪切应力平均值为133.94 MPa，方差为163.56 MPa；间隔分布时螺栓所受的最大剪切应力平均值为108.11 MPa，方差为4.41 MPa。因此，在齿轮齿条钻机提升装置运行过程中，螺栓组采用非均匀分布时，单个螺栓所受剪切应力较小且齿条受载比较平稳。表5与表6表明：通过有限元计算获得的各铰制孔螺栓的剪切应力与计算结果十分接近，误差在10%以内，表明弹簧刚度法具有较高的精度。进一步对比螺栓在两种不同分布方式下的最大剪切应力，可以看出有限元计算结果大于理论计算结果，主要是由于在理论计算过程中，未充分考虑预紧力以及齿条本身重力对螺栓剪切应力的影响。且在对齿条施加载荷时，也不能完全与理论设计的位置保持一致。使得两者间存在微小的误差。但齿轮齿条钻机在载荷移动过程中，有限元分析得到的螺栓最大剪切应力与理论计算出的最大剪切应力随螺栓位置变化规律一致。所以有限元分析所得结果与理论数据具有一致性。

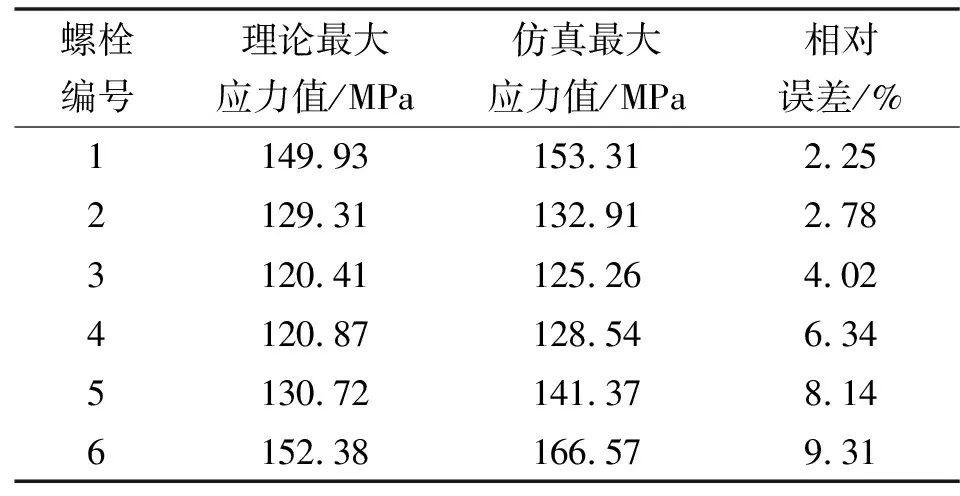
表5 螺栓均匀分布时螺栓最大剪切应力

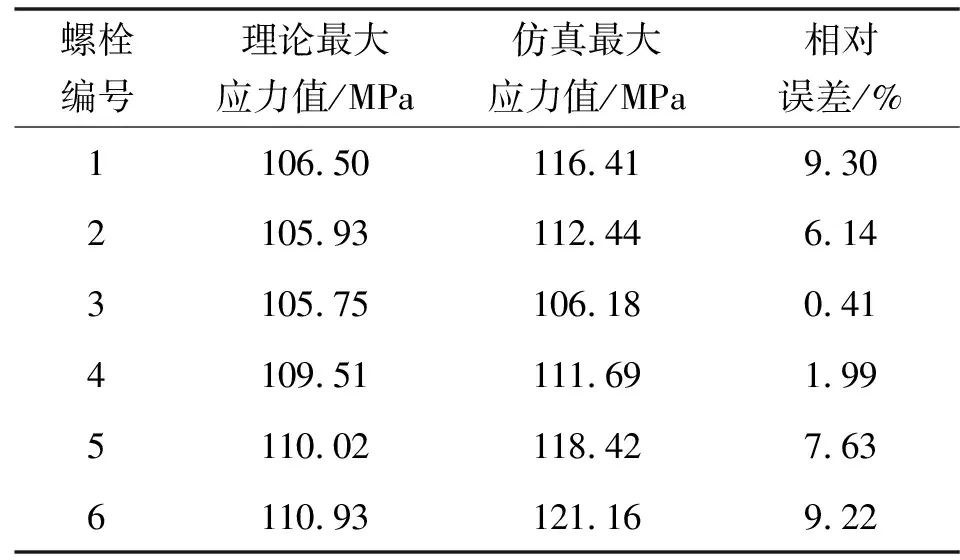
表6 螺栓非均匀分布时螺栓最大剪切应力

4 结论

螺栓分布策略会影响大型重载机构的安全稳定，本文作者基于弹簧刚度法，给出了考虑结构复杂连接件的多螺栓连接载荷计算方法。计算了螺栓应力的分布规律，并通过对多螺栓连接实例的准静态试验与有限元仿真分析对该方法的准确性进行了验证，得到以下结论：

(1)根据准静态试验结果，螺栓载荷分布与螺栓的分布策略密切相关。在相同结构尺寸时，非均匀螺栓分布的承载分布均匀性要优于均匀分布的螺栓。

(2)采用所建立的多螺栓连接模型，并对模型参数进行适当的调整，可以对不同螺栓间距的螺栓载荷分布情况进行预测。试验与有限元结果表明：所提出的螺栓载荷计算方法具有较高的准确性。

(3)提出了复杂空间桁架结构的刚度计算方法，为了便于计算，引入了等效高度系数，根据该系数可计算出螺栓载荷波动最小的螺栓间距。但在螺栓之间桁架结构不同时吻合程度相对较差，因而在进一步对模型精细化研究时需对不同结构进行考虑。