直线型柱塞式平衡调节阀结构优化研究

于正昌，郭健翔，2，张龙，孙晋飞，2，刘占杰

(1.青岛理工大学环境与市政工程学院，山东青岛266525；2.山东省余热利用及节能装备重点实验室，山东青岛266525)

0 前言

静态水力失调是一种发生在空调和采暖系统中固有的水力失调，通常通过设置静态平衡阀达到平衡各个环路的目的[1]。静态平衡阀需要明确流量-压差-开度对应关系即Kv曲线，实现只测量阀门两端压差便能计算出某一开度下的流量的目的[2]。常见的阀门流量特征有4种[3]，分别是直线型、等百分比型、快开型以及抛物线型。相比较来说，直线型流量特征更直观地表现了Kv值与开度的对应关系，并可以通过线性拟合得出较准确的函数关系，更加适合作为静态平衡阀的流量特征。

随着调节阀种类越来越多，经验公式已经无法适用于所有新型阀门的设计，需要进行大量试验对阀门结构逐渐调整，且每次调整结构都需要重新制作样阀，耗费了大量社会资源。计算流体力学应运而出，在阀门研发上的应用越来越广泛。众多学者针对不同结构的调节阀，就阀内的流动情况、空化气蚀现象以及调节阀的流量特性都进行了大量研究。徐宏海等[4]对内部复杂的调节阀流场进行了三维模拟，通过比较调节阀的理论流量系数和模拟计算值，发现两者吻合良好、误差较小，验证了将CFD技术应用于调节阀流场的可行性并为其他阀门的模拟提供了参考。赵莹[5]以液体火箭发动机用球阀为例，模拟定流量和变流量条件下的流场，得到了流量系数与球阀开度的对应关系，并辅以相关实验进行验证，发现仿真结果与实验结果高度一致。由于仿真模拟结果的可视化，众多学者借助CFD技术观察到调节阀内部不稳定因素，并依据相关经验对阀门结构进行优化，以降低甚至消除不利因素的影响。吴佳宝[6]以轴流式止回阀作为研究对象，通过对阀芯以及流道型线的分析和优化，消除了阀门中回流、速度分布不均以及流体拥塞等现象，并配合流阻系数试验验证了模拟的准确性。为了使压力调节阀安全可靠地应用在输油管线中，魏丹[7]借助仿真模拟软件Fluent找出阀门现有的不足，进而对齿形串级结构以及二级节流孔形状进行一定优化，并与优化前对比发现，优化后的阀门内部流动更加稳定。

本文作者以数值模拟为主、实验测试为辅验证模拟方案的正确性，从而保证优化平衡阀结构的可靠性。

1 调节阀原始结构建模仿真

1.1 物理模型建立

对DA-J80-40-00静态平衡阀进行物理建模，总体结构如图1所示。该柱塞式调节阀由阀体、阀盖、手轮、阀杆、阀瓣、阀芯、紧锁杆以及相关密封圈组成。该阀门调节原理为：旋转阀门手轮，阀杆随之转动，带动阀瓣升降，达到调节阀芯与阀座距离的目的，实现开度调节。阀门开度改变，流体流经阀门的阻力也随之改变，达到调节流量的目的。

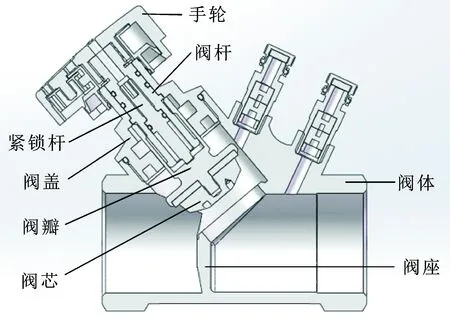
图1 调节阀三维结构剖面图

为保证调节阀内部流动模拟结果的准确性，按照阀门测试的标准进行管道设置[8]，在阀门进口端添加一段5D的直管段，在阀门出口添加一段10D的直管段。总体结构如图2所示，流道模型如图3所示。在计算阀门两端压降时，采用公式(1)：

Δpv=Δp1-Δp2

(1)

式中：Δpv代表流体流经阀门两端的压降；Δp1代表流体流经整个系统的压降；Δp2代表流体流经进出口总长度直管段的压降(单独进行模拟计算)。

图2 直管段-调节阀总体结构

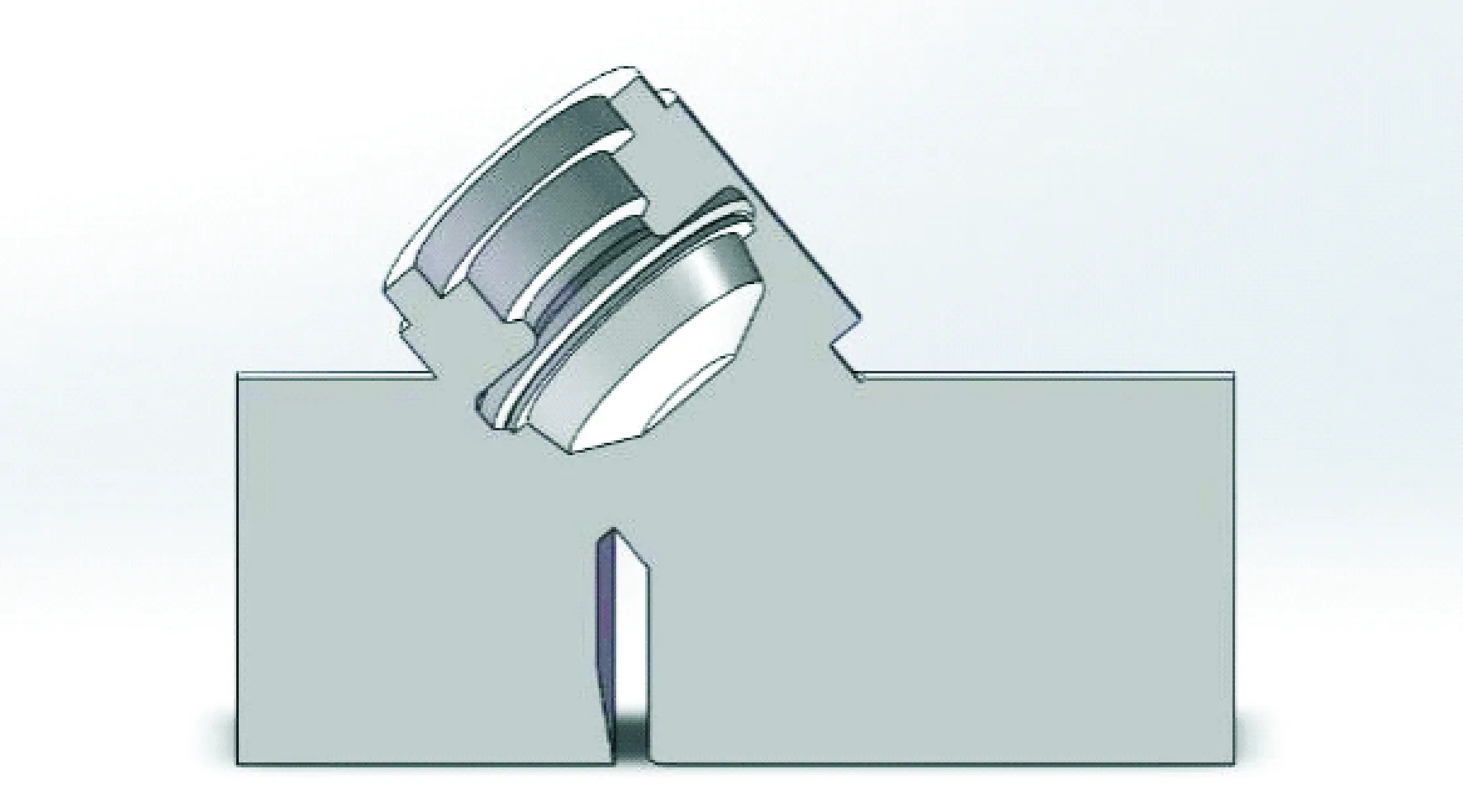
图3 调节阀全开时流道模型

1.2 网格无关性验证

以调节阀全开状态的流道为例作网格无关性验证，分别划分5.4×105、7.4×105、9.4×105以及1.09×106这4种不同数量网格，网格质量均稳定在0.4以上、网格倾斜度均在0.84以下。设置的边界条件均是2 m/s的速度进口以及101.3 kPa的压力出口，以该速度进口条件下的质量流量M=3.175 1 kg/s为标准值，获得网格无关性检验结果如表1所示。随着网格数量增大到7.4×105，模拟结果就已经相差不大了，综合考虑7.4×105为适宜的网格数量。

表1 网格无关性验证

1.3 求解与边界条件设置

文中选用定流量以及定压降2种工况，取2种工况下的平均值作为模拟值，2种工况边界条件设置如表2所示。在流动过程中，流体会在阀芯处产生绕流，故采用Realizableκ-ε紊流模型[9]；压力速度耦合算法采用 SIMPLE 算法，压力插值方式采用二阶插值方式，单元中心的变量梯度选择Least Squares Cell Based，其他项采用二阶迎风插值，计算至收敛。

表2 边界条件设置

1.4 结果分析

通过对模拟数据的整理，按照公式(2)，计算得出阀门每个开度下的Kv值，并绘制Kv曲线观察分析该阀门的流量特性。相关数据记录见表3、4。

(2)

式中：Q为某一开度下的阀门流量，m3/h；ρ0为水在15 ℃下的密度，一般情况下认为ρ0/ρ=1；Δpv为某一开度下阀门两端的压差，kPa。

由表3、4可以看出：随着阀门开度增大，在定流量工况时，流体通过阀门的压降变小；在定压降工况时，流体通过阀门的流量增大，可见随着阀门开度增大，阀门流通能力变好。

表3 流量系数(定压降工况)

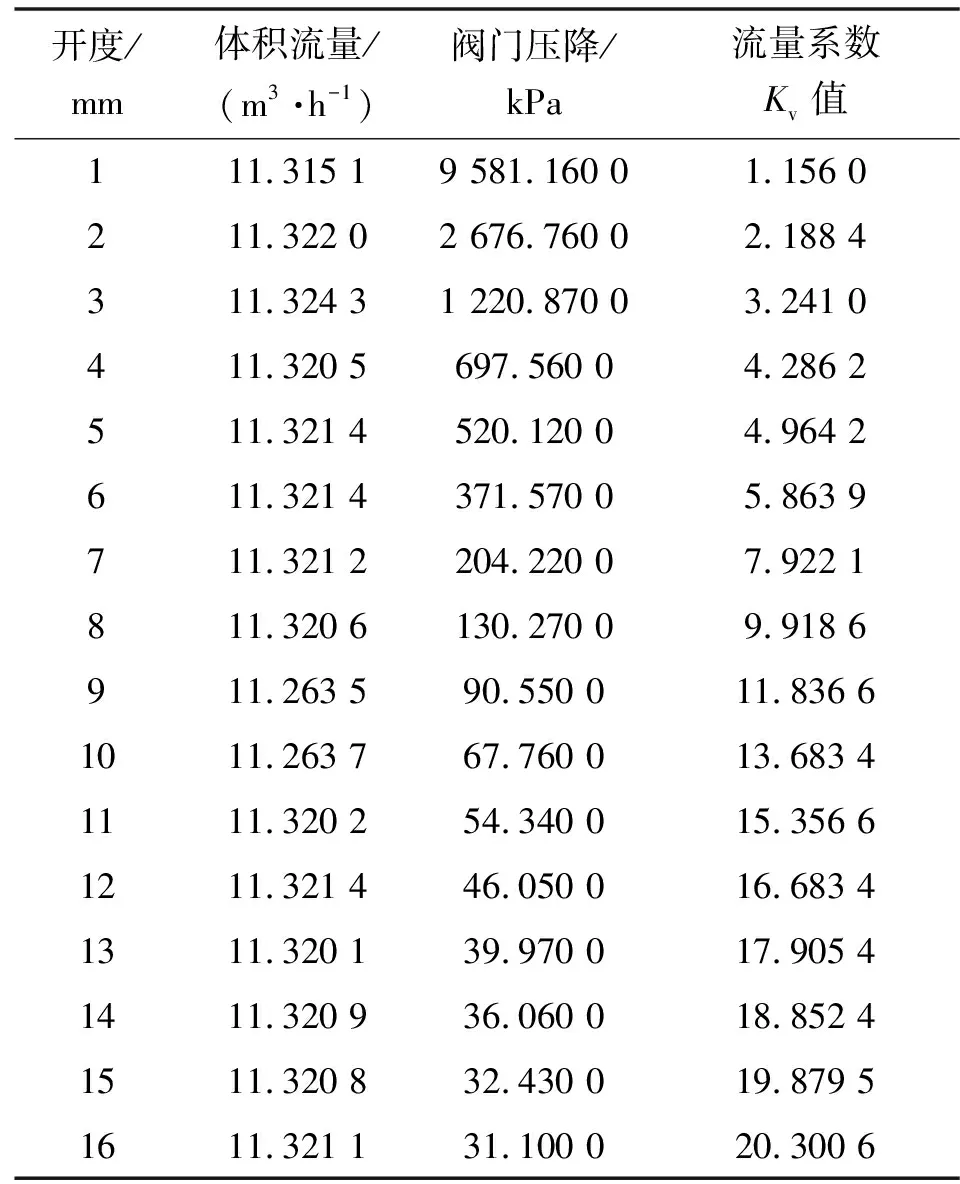
表4 流量系数(定流量工况)

2 可行性分析

2.1 实验测试

数值模拟可以清晰地观察到调节阀内的复杂流动，但是在数值模拟复杂流动的过程中，采用的数学模型以及仿真方案可能会与实际情况有所偏差。因此对调节阀进行一定的实验不仅可以检测调节阀实际情况，同时也能对数值模拟的准确性进行验证。实验装置如图4所示。

试验过程中，固定试验阀门的开度，调节下游阀门的开度，使试验流量在容许范围内，并在10 s后观测流量计。试验所用的电磁流量计和压力传感器的精度均在规定范围内。在确定流量时，最大值与极小值之差不应超过偏离平均值的1.2%。为了使测试结果尽可能准确，要在流量和压差稳定的情况下读写测试数据。特定的操作是每个流程都有5 s以上的时间间隔，同时记录流程和压差。该被测阀门为手动调节阀，阀芯行程为16 mm，手轮可以旋转4圈，故选择8个开度进行测试，记录调节阀在不同开度下的流量和阀门两端的压力差，相同开度下记录4次测试数据，整理数据如表5所示。

2.2 可行性分析

通过试验测试得到了阀门部分开度的Kv值，将它与同样开度下的模拟数据进行对比验证数值模拟的可行性，相关数据如表6所示。

表6 流量系数对比

由表6可知：模拟数据和实测数据高度吻合，忽略模拟中残差收敛情况以及实际流动中一些不稳定因素所造成的影响，两者基本一致。在小开度时，模拟值略大，这因为模拟相对理想，而实测数据存在误差。在实际流动中，同样流量下的小开度阀门闭合度较高，导致流体容易撞击到阀门内部各处都会产生压降，因此阀门流量系数模拟值比实测值略大一些。在大开度时，同样流量下，实际流动较为平稳，这时更容易受到重力以及涡流等一些不稳定因素的影响，导致实测值要比模拟值略小一些。通过分析得出模拟方案可行，模拟数据可靠，后面将以模拟数据为标杆进行对阀门结构的优化。

3 阀芯优化

3.1 优化方案

设计优化是一种通过充分利用和探索系统中相互作用的协同机制设计复杂系统和子系统的方法[10]。

为了得到具有线性流量系数曲线的柱塞式调节阀阀芯形状，首先需要利用数值模拟计算原始阀芯各开度下的流量系数，得到各开度下流量系数增量ΔKv，利用数学统计方法，获取流量系数增量ΔKv样本分布均值，以计算理论流量系数；比较理论流量系数与实际流量系数的差别，根据流量系数受流通面积影响的思路修改阀芯形状，计算修改阀芯后的调节阀各开度流量系数，重新获取样本均值及样本标准差，计算理论流量系数增量ΔKv，进而修正阀芯形状；最终保证线性流量系数曲线在比较均衡的水平下，完成阀芯的设计优化。阀芯的设计流程如图5所示，在该设计方案中，以流量系数曲线和流量系数增量ΔKv共同作为评价标准。

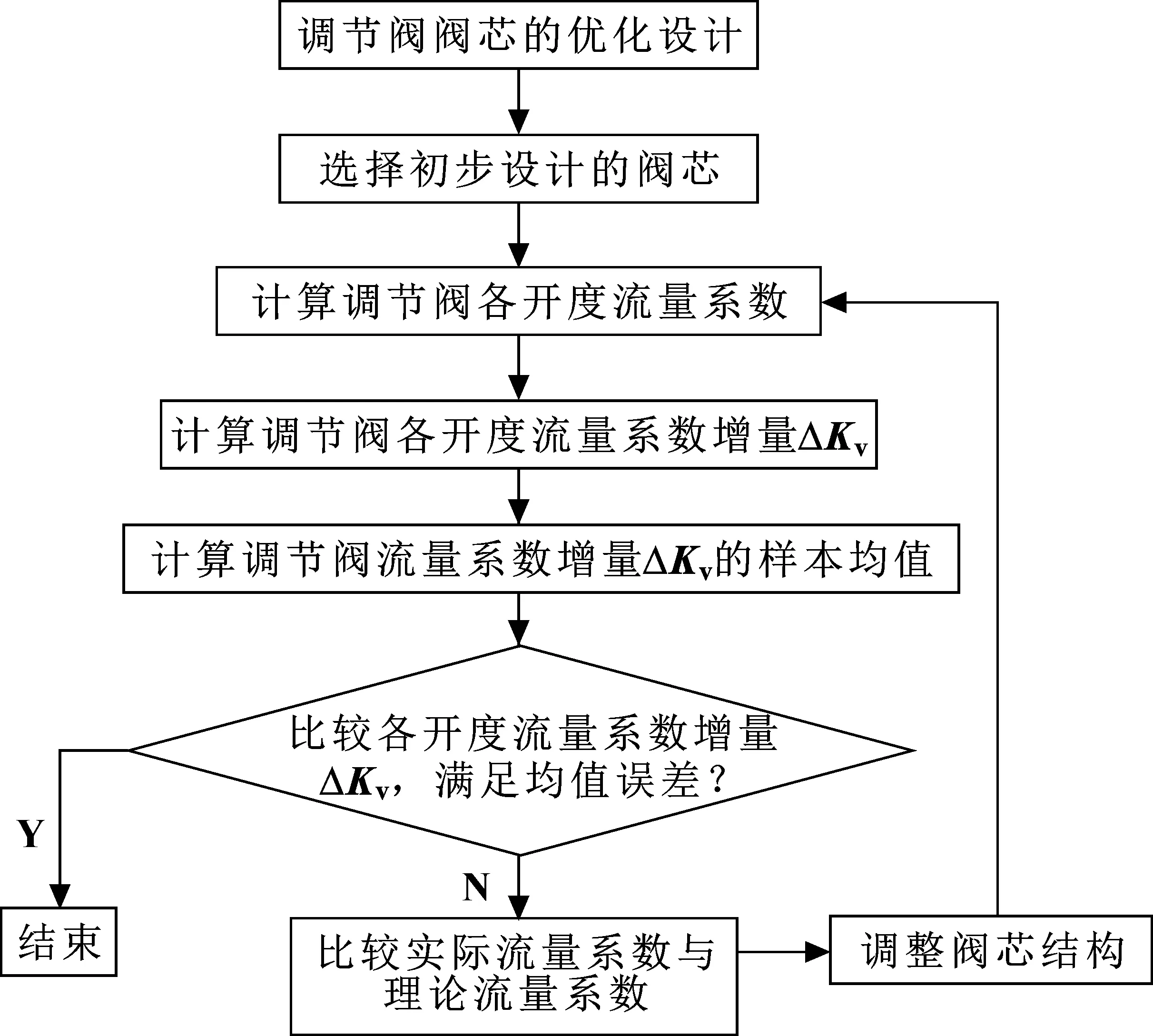
图5 优化方案流程

3.2 优化步骤与分析

对于此柱塞式调节阀，已知其额定流量系数为20，阀芯行程为16 mm，则可作出该调节阀的理论流量系数曲线以及各开度下的流量系数增量ΔKv均为1.25，将1.25作为流量系数增量的样本均值，省略了上述方案中反复计算调节阀流量系数增量ΔKv样本均值的步骤。

为了方便对阀芯结构进行分段优化，在不影响调节阀流量特性的前提下，先将阀芯原有结构形状沿着BC段进行延伸，阀芯长度由9.9 mm增至12 mm，具体结构变化如图6所示。

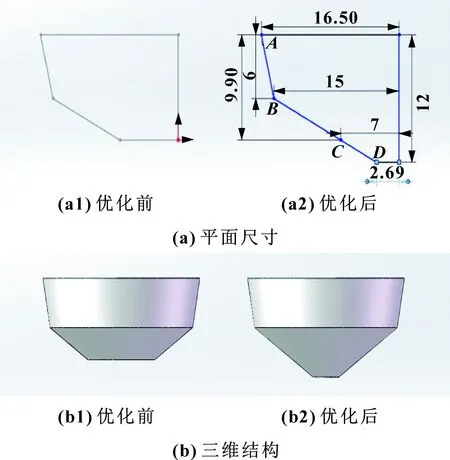
图6 阀芯延伸示意

通过数值模拟结果发现将阀芯沿着BC段原有的斜率延伸至点D，对调节阀现有流量特性不产生影响。由表7可知：在优化阀芯前，调节阀1-8 mm开度下的流量系数明显小于理论值，故需要调整阀芯结构使其流通面积变大以使流量系数提高；而在9-16 mm开度下的流量系数明显大于理论值，故需要调整阀芯结构减小流通面积使其流量系数降低，因此，对阀芯的优化从小开度和大开度逐个出发。

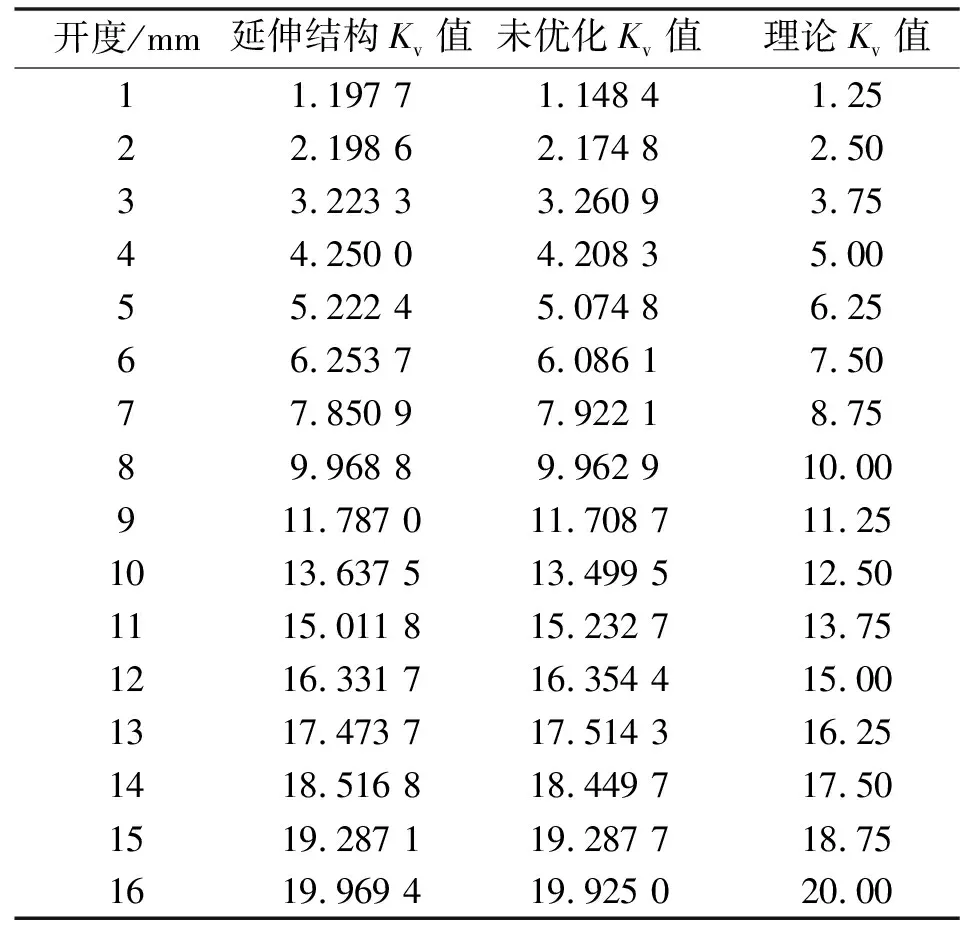
表7 流量系数对比

由于该调节阀为柱塞式，则阀芯的上部分结构即AB段对调节阀小开度流量特性影响较大，阀芯的下半部分结构即BD段对调节阀大开度流量特性影响较大，且小开度下的流量特性基本只受阀芯AB段影响，所以按照以下步骤开始对调节阀的优化。

(1)优化调节阀阀芯AB段结构，在ACD3点确定的前提下，调整点B与阀芯对称线之间的距离。调整时以0.1 mm为单位，每次调整后对16个开度下的模拟结果进行汇总，发现由优化前的15 mm调整为14.6 mm，可使得调节阀小开度时流量特性较接近线性。具体尺寸变动以及结构变化如图7所示。

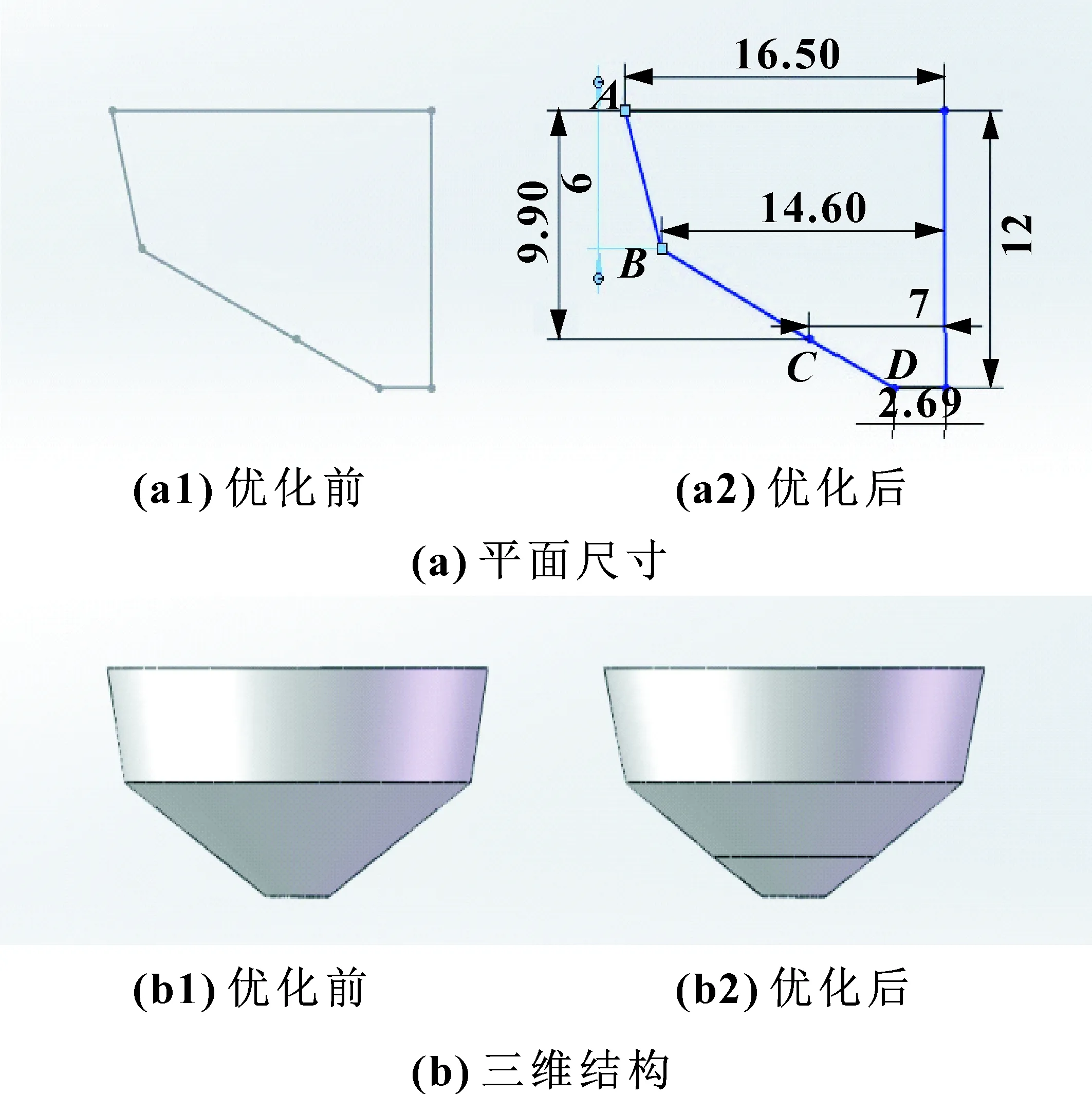
图7 阀芯第一段结构改动

(2)优化调节阀阀芯BC段结构，在ABD3点确定的前提下，调整点C与阀芯对称线之间的距离。调整时以0.2 mm为单位，每次调整结构后对16个开度下模拟结果进行汇总，发现由优化前的7 mm调整为12.2 mm，可使得调节阀在9-14 mm的开度区间下流量特性呈线性。具体尺寸变动以及结构变化如图8所示。

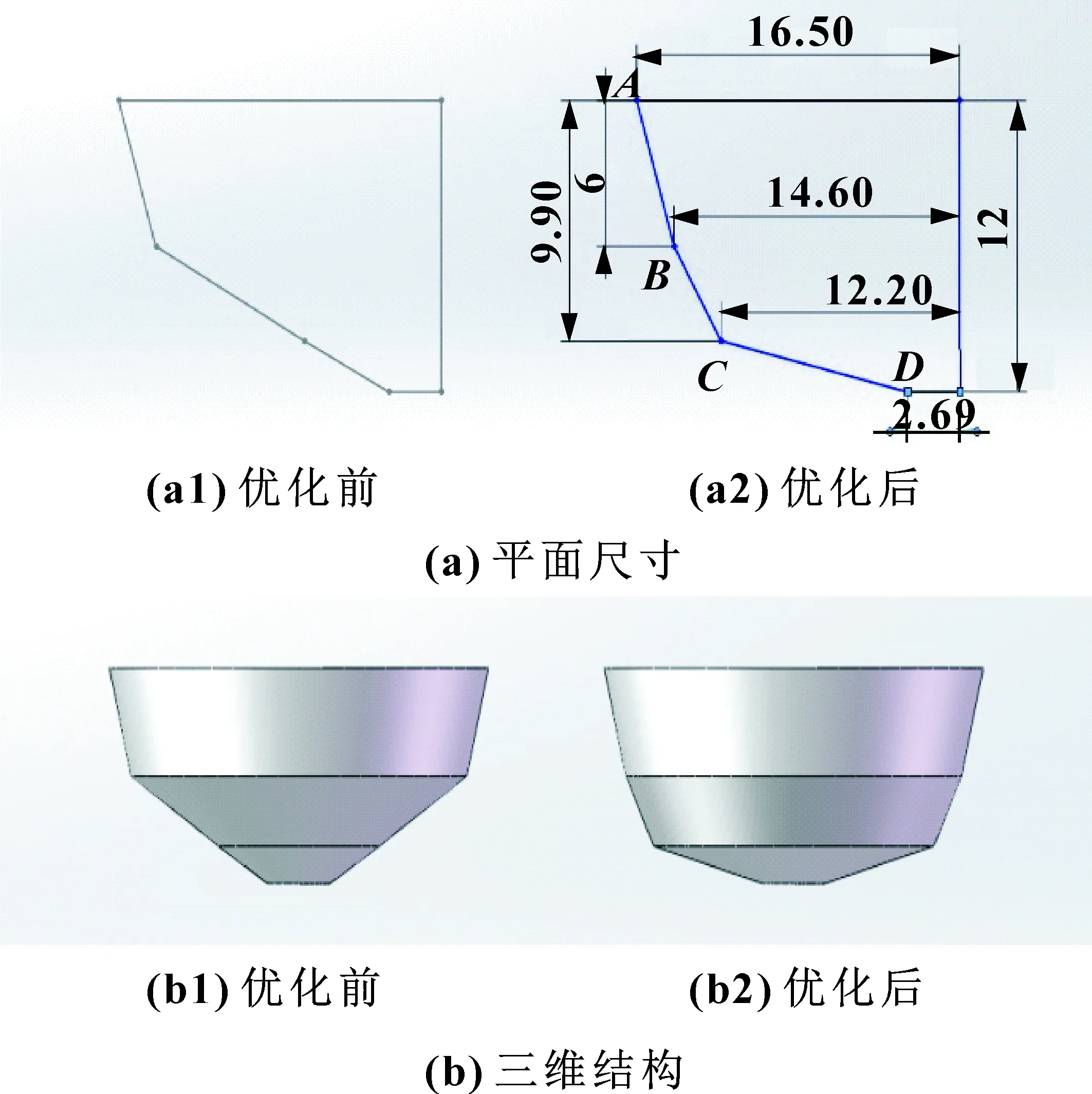
图8 阀芯第二段结构改动

(3)优化调节阀阀芯CD段结构，由于ABC3点都已经确定，故调整点D与阀芯对称线之间的距离。调整时以1 mm为单位，每次调整结构后对16个开度下模拟结果进行汇总，发现点D与阀芯对称线重合时，可使得15、16 mm两开度下的流量系数更加贴合线性。具体尺寸变动以及结构变化如图9所示。

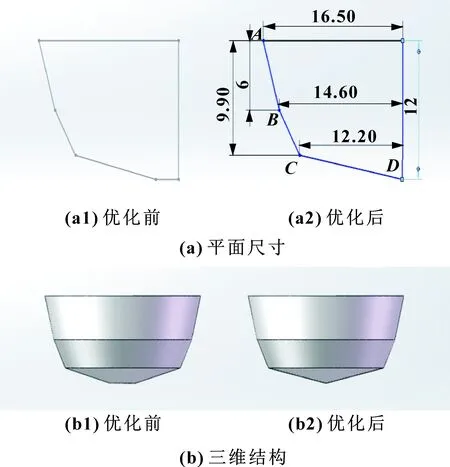
图9 阀芯第三段结构改动

经过以上3次对阀芯结构的分段调整优化，调节阀的流量特征已较贴合直线形，且对它进行仿真模拟时，以1 mm为开度的调节单位，因此，模拟得出的线性流量特征具有较高的可信度。相关数据汇总如表8、9所示。

如表8所示，第一段优化后，1-8 mm开度下的流量系数与理论值已经高度吻合，进一步验证了1-8 mm开度下的流量系数基本只受阀芯AB段影响；经过第一段、第二段优化后，9-14 mm开度下的流量系数与理论值一致，但由于点C与阀芯对称线之间的距离从之前的7 mm扩大为12.2 mm，导致调节阀15、16 mm 2个开度下的流量系数变小，此现象表明调节阀的大开度流量特性较容易受到阀芯下半部分结构的影响；则通过第三段优化，将点D向阀芯对称线靠拢，使得调节阀15、16 mm开度下的流量系数增大并与理论值更加贴合。经过3段优化后的阀芯流量特性高度贴合直线形。

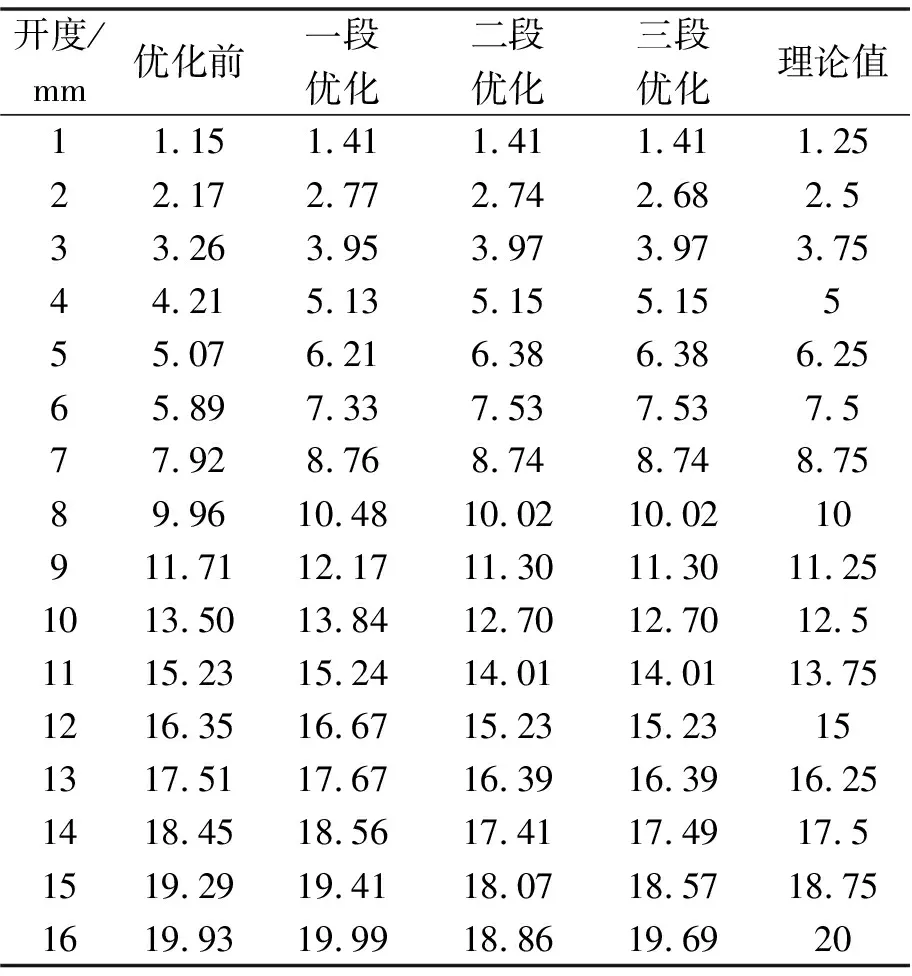
表8 各优化阶段流量系数

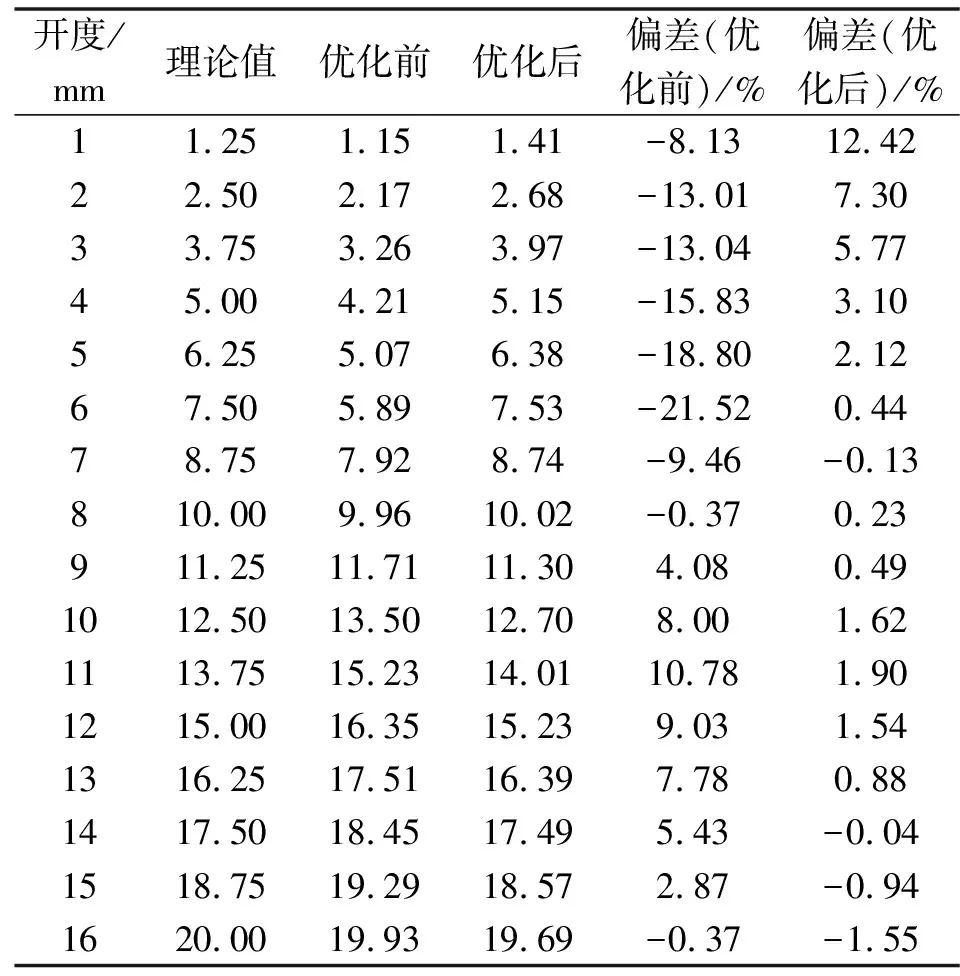
表9 优化前后流量系数偏差

为更好地分析各阶段的线性关系，运用数学方法对调节阀各开度流量系数增量进行分析，采用误差和标准差2种方法，计算误差和标准差时均以流量系数理论单位增量1.25为样本均值，相关数据统计如表10、11所示。

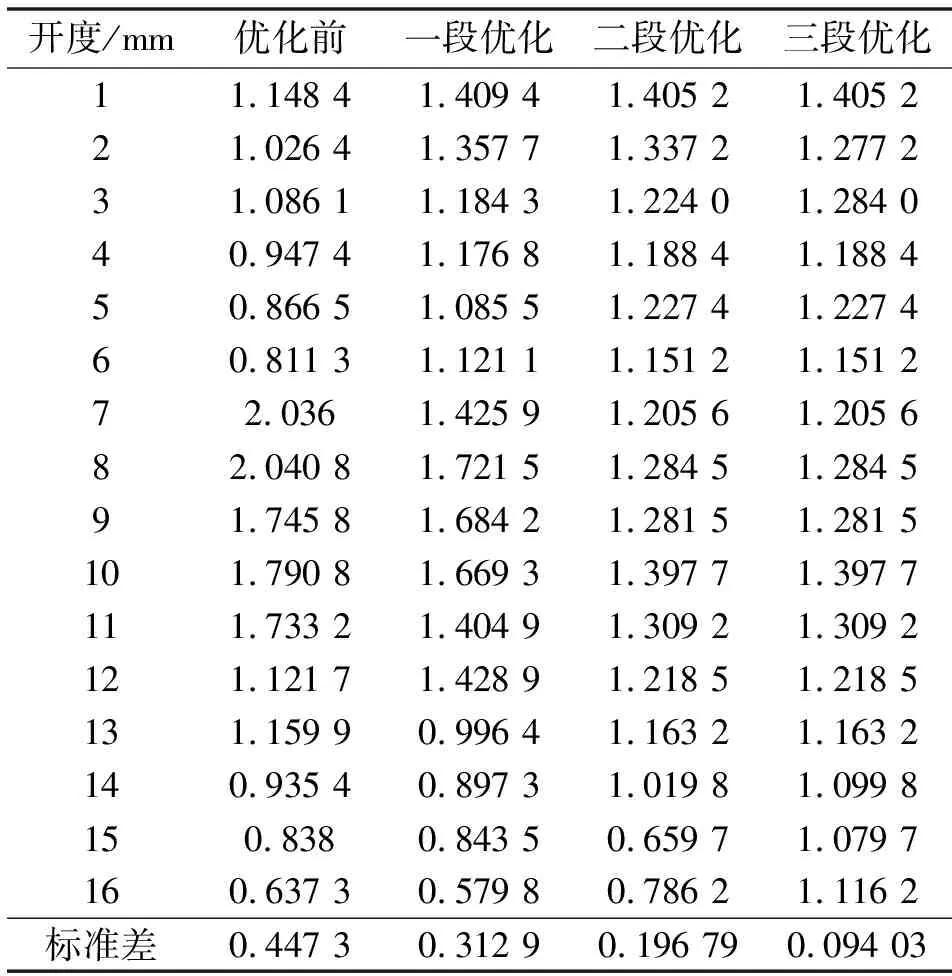
表10 各优化阶段流量系数增量

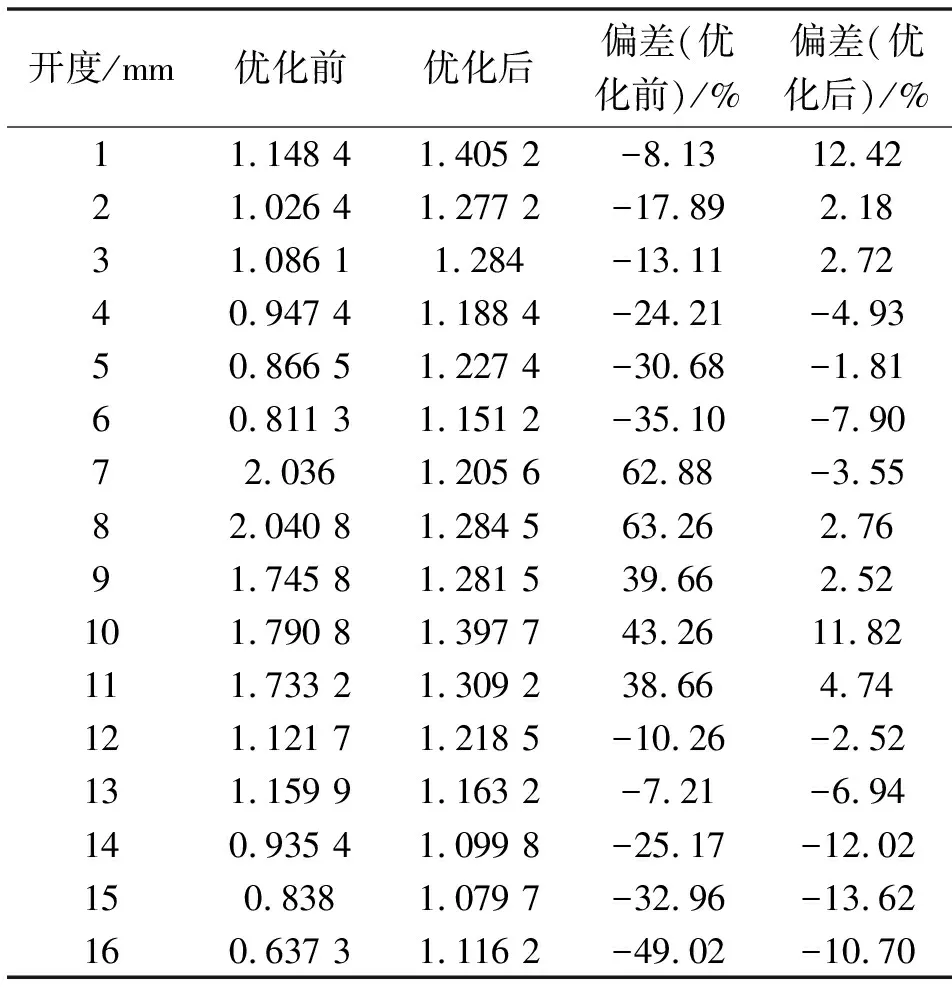
表11 优化前后流量系数增量与理论值偏差对比

标准差作为数理统计中反映个体间离散程度的量，其值越小代表样本越集中稳定。由表10可以看出，进行3段优化后的流量系数增量的标准差仅为0.094，与未优化结构前的标准差相比少了0.353，故3段优化后的流量系数增量较集中稳定。由表11可以看出：经过3次分段优化后，流量系数增量较理论值最大偏差由未优化前的63.26%降为13.62%，最小偏差由未优化前的7.21%降低为1.81%，均满足在±15%的偏差内。

4 结论

文中主要阐述一种柱塞式调节阀阀芯的优化设计方案，并通过对DA-J80-40-00型静态平衡阀的实际优化验证优化方案的合理性和正确性。针对此优化方案进行的实际工作可得出以下结论：(1)以流量系数和流量系数增量共同作为评判线性贴合度的准则，可以保证优化后的流量特性满足实际线性需求；(2)对于柱塞式调节阀阀芯结构的优化，采用分段方式可以快速且准确地完成优化；(3)该方案可进一步提升阀门的调节精度，使阀门在管网中运行时更加稳定精确。