石榴子石的LA-ICP-MS面扫描U-Th-Pb定年——以铜绿山大型Cu-Fe-Au矽卡岩矿床为例*

葛粲 汤笑伟 汪方跃 李修钰 孙贺 顾海欧 袁峰 郑辉

矽卡岩矿床是最具有经济价值的金属矿床之一,是铜、钨、金、银、锡、钼、钴等稀有金属的重要来源(周涛发等,2017)。矽卡岩矿床年龄的厘定对研究矿床成因、演变过程、成矿规律和找矿勘查具有重要意义,矽卡岩中的锆石、锡石、白钨矿、石榴子石等副矿物均可为矽卡岩矿床研究提供同位素年代学证据(Lietal.,2010,2023;Zhouetal.,2019;次仁拉姆等,2021)。

在同位素定年方法中,激光剥蚀电感耦合等离子体质谱仪(LA-ICP-MS)分析方法相对于同位素稀释热电离质谱(ID-TIMS)和二次离子质谱((SIMS)等方法,具有效率高、成本低等优点,其研究对象也从最初的锆石逐渐扩展到金红石(Luvizottoetal.,2009;Zacketal.,2011;Houetal.,2020)、符山石(Weietal.,2022;Zhangetal.,2022)、磷灰石(Chewetal.,2011)、独居石(Paquette and Tiepolo,2007;Luoetal.,2018)、石榴子石(Dengetal.,2017;Semanetal.,2017;Wangetal.,2022)、榍石(Storeyetal.,2007)、白钨矿(Tangetal.,2022)、黑钨矿(Luoetal.,2019;Yangetal.,2020;Carretal.,2021;杨岳衡等,2021)、褐帘石(Darlingetal.,2012;Burnetal.,2017)、绿帘石(Peverellietal.,2021)、方解石(Robertsetal.,2017;Drostetal.,2018)、石膏(Beranoaguirreetal.,2022)、锡石(Yuanetal.,2011;Yangetal.,2022)等。正因如此,近年来利用该技术进行副矿物定年的研究比例在大幅提升(罗涛和胡兆初,2022)。

石榴子石是矽卡岩中普遍存在的矿物,其地球化学信息常用于矽卡岩矿床研究(Jamtveitetal.,1993;Smithetal.,2004;刘晓菲等,2014)。石榴子石具有较高的U-Pb同位素封闭体系温度(>850℃)和较好的晶形结构(Mezgeretal.,1989;Meinertetal.,2005)。近些年的研究表明,石榴子石具有相对高U的特征,可作为LA-ICP-MS U-Pb测年的目标矿物,为矽卡岩的成矿提供年代学证据(Dengetal.,2017;Semanetal.,2017;林彬等,2020;张小波等,2020;Chaoetal.,2023)。

目前,LA-ICP-MS石榴子石定年主要使用的是点分析技术。因为LA-ICP-MS分析的准确性和精密度相对较差,所以需要通过对一个样品进行多次重复测量和分析,来提高分析的准确度和精密度来计算其加权年龄。目前点分析技术存在着包括深度分馏、基体效应、普通Pb校正等诸多问题。其中,深度分馏问题表现为随着单点剥蚀深度的加大,分析信号快速降低,同时同位素比值出现线性或非线性分馏变化。围绕这个难题,前人设计了活动聚焦(Hirata and Nesbitt,1995)、线剥蚀(Lietal.,2001;Horstwoodetal.,2003;Slámaetal.,2008)、添加辅助气体(Luoetal.,2018)等测试方法,以及如截距法(Chewetal.,2011)、数学模型校正法(Patonetal.,2010;Ver Hoeveetal.,2018)等各种数据处理校正方法。但这些方法依旧存在一些问题,如截距法与剥蚀信号段的起始时间设定有关,由于部分LA-ICP-MS仪器的激光触发开关是手动的,导致无法准确确定剥蚀信号起始时间,因此其截距值随着人工设定的起始时间变化而变化;而我们在对磷灰石样品的实验测试中发现,不同的磷灰石表现出相异的深度分馏特征,如果采用其中一组作为标样获得校正函数,并应用到其他样品时,会导致校正数据产生更大偏离,导致深度分馏校正失败。

基体不匹配问题是影响LA-ICP-MS高精度定年的另一个关键问题。由于不同矿物的激光分析行为不完全一致,元素化学分馏存在一定差异,基体不匹配可能导致定年结果出现系统性偏差(Liuetal.,2011;El Korh,2013, 2014;Yangetal., 2018)。因此需要开发基体匹配的年龄标样。然而,当前高质量副矿物定年标准样品的极度缺乏严重制约着副矿物年代学的广泛应用(罗涛和胡兆初,2022)。目前,最通用的年龄标样为锆石。而对于当前流行的非锆石类副矿物,由于其结构中不能排除普通Pb的加入,因此在这些副矿物年龄标样开发过程中,样品量充足且满足元素/同位素比值均一的副矿物定年标样的开发难度远大于锆石定年标样的开发。目前已发表的副矿物标准特征似乎表现为极低的普通Pb特征,适用于分发予全世界同类型的激光实验室。然而,实际的测试结果显示,分发的副矿物标样存在铀含量低、含矿物包裹体、普通铅比例不均一等缺点,实测的铀铅同位素比值并非像锆石标样的一样稳定,从而导致分馏系数计算波动较大。由于标样开发难度较高,目前我国用于副矿物U-Pb年龄微区分析的标样极少(Lietal.,2013;Huetal.,2021;罗涛和胡兆初,2022),其中包括石榴子石标样的缺乏(Lietal.,2022),这也导致目前多数研究仍然使用锆石作为首选定年标样(Dengetal.,2017;陈靖等,2021;Tangetal.,2022;Zhangetal.,2023)。

含普通Pb矿物的普通铅校正也存在一定的问题。由于含普通Pb矿物中的204Pb含量极少,且LA-ICPMS分析过程中204Pb容易受到204Hg的干扰,所以难以采用204Pb进行普通Pb扣除(Horstwoodetal.,2003)。除了金红石、榍石等钍含量较低的副矿物,可以用208Pb法进行普通铅校正外(Sunetal.,2012;Braccialietal.,2013),其他含普通铅副矿物通常需要借助Tera-Wasserburg(TW)(Tera and Wasserburg,1972)图解进行普通铅校正。因此,为了获得含普通铅矿物的准确年龄,分析的选点十分重要,只有在TW图解中获得不同U/Pb比值的测量数据,才有利于进行线性方程拟合获取交点年龄,在不知道U/Pb比值信息的情况下盲目实验,增加了失败的风险。当出现测量数据点太少、或数据点集中在高普通铅区域而造成数据点分布不合理时,往往导致无法准确确定交点年龄。需要通过额外引入约束条件,如采用与待测副矿物同期形成的低U矿物(如长石、方铅矿等)铅同位素组成或地球铅同位素演化模型(Stacey and Kramers,1975)获得TW图中的截距锚点来进行207Pb法校正。

LA-ICP-MS面扫描是近些年来发展的一种新的元素空间分析方法,该方法能很好地展示出低含量元素在矿物中的分布特征(汪方跃等,2017;Chewetal.,2021)。在碳酸盐U-Pb定年方法的早期开发过程中,大多数实验室为提高定年成功率,在开展矿物元素面扫描工作基础上,选择高U、低Pb区域进行点分析定年,这种方案已经大大提高测试的成功率(Hoareauetal.,2021;Wuetal.,2022)。Drost对碳酸盐的U-Pb定年时采用了面扫描分析,首次提出通过面扫描方法进行预分析来获得高精度U-Pb定年方案(Drostetal.,2018)。LA-ICP-MS面扫描定年分析方法主要是通过对样品进行逐行线扫描获取数据(汪方跃等,2017),采集矿物的U、Th、Pb同位素和其他微量元素信息,进行定年分析。基于面扫描技术的U-Pb定年方法在以下4个方面比点剥蚀有优势:(1)面扫描获得元素的二维分布图,可以剔除包裹体等异常数据的干扰,有利于样品的初次筛选;(2)减弱深度分馏效应,面扫描分析通过线剥蚀样品表面的物质,深度分馏效应问题可以忽略;(3)分析效率极大提高(成功率),该方法不需要二次选点再次点分析实验,这无疑提高了分析效率,并且避免了点分析中的选点难题;(4)定年准确度提升,由于面扫描分析可以获得海量数据,大量不同比例普通Pb分布的矿物分析有望建立起更为准确的TW等时线交点,使得数据的准确度提高。

然而,采用面扫描技术也面临新的问题。由于面扫描获得的数据波动性大,且精度不高,因此含普通铅的矿物面扫描数据在TW图中离散度很大,所以直接用最小二乘拟合直线方程会得到错误的交点年龄。本文提出了一种利用LA-ICP-MS面扫描数据构造虚拟点获得TW图交点年龄及误差的定年分析方法,该方法在获得样品原位微量元素含量分布的同时可以获得准确的年龄信息,为当前矽卡岩型相关的关键金属矿床年代学研究和成岩研究提供更为有效且便捷的手段。

1 理论推导

LA-ICP-MS的单次测量准确性较差,但是通过增加测量样本容量进行反复测量,可以提升同位素比值点估计的准确性,降低测量误差。通过对面扫描数据进行关联数据统计分析,抽取理论上落在TW图中相同点的数据,对测量数据进行重新分组抽样,构建多个抽样集合。每个抽样集合中同位素比值的数据可以形成一个虚拟点,由于每个虚拟点由多个测量点构成,其期望值相对单次测量数据点更接近真值,同时通过多次测量也有了对该虚拟点的误差估计。如何从海量的面扫描数据中抽取理论上位于TW图中相同位置、却由于测量误差而导致分散的数据点,这就需要分析TW图中的理论点位置依赖于何种控制因素。

1.1 TW图理论位置依赖因素分析

在TW图中,x轴是现今的238U/206Pb,y轴是现今的207Pb/206Pb,因此TW图中任意点(x,y)可以用公式(1)表示:

(1)

由于现今的Pb包括了初始的普通铅(Pbc)和由放射性元素产生的放射铅(Pb*),利用公式(2)表示:

(2)

而矿物生成时,矿物各处的铅和铀含量不均匀,因此,各处的初始普通铅与现今铀的比值是不定的,假设:

α=206Pbc/238U

(3)

TW图中包含了两种铅的同位素,假设初始普通铅同位素比值为:

b=207Pbc/206Pbc

(4)

设矿物形成后一直封闭演化了t(Myr),即矿物年龄为t(Ma),由现今的U的含量可以推算出现今放射铅206Pb*和207Pb*含量,得到公式(5)和公式(6):

206Pb*=238U(eλ8t-1)

(5)

207Pb*=235U(eλ5t-1)

(6)

上式中,λ8=1.55125×10-4/Myr和λ5=9.8485×10-4/Myr是放射性元素238U和235U的衰变常数;e是自然底数。

由于,现今的238U/235U=137.818(Hiessetal.,2012),所以通过公式(6)可得到公式(7):

207Pb*=238U(eλ5t-1)/137.818

(7)

将公式(2)、(3)、(4)、(5)、(7)代入公式(1),获得公式(8)。这样可以推导出TW反谐和图中任意点(x,y)与矿物年龄,普通铅同位素比值以及初始普通铅与铀的比值关系:

(8)

由公式(8)可以看出,一个确定矿物(b和t是定值)的TW图中理论数据点的位置(x,y)由初始铅铀比α唯一确定。如果初始铅铀比α为0,即矿物内不包含初始铅的区域,现今的数据会落在TW图的反谐和曲线上,利用公式(9)表示:

(9)

如果初始铅铀比α为∞,即矿物中铀含量极低(趋向于0),或普通铅含量极高、远高于放射性铅,现今的数据会落在TW图的y轴截距位置,利用公式(10)表示:

(10)

设矿物任意两处初始普通铅与现今铀的206Pbc/238U的比值分别是α1和α2,矿物经过时间t(Myr)演化后,分别落在TW图的(x1,y1)和(x2,y2)两点,可以利用公式(11)计算斜率k:

k=(y2-y1)/(x2-x1)

(11)

将公式(8)带入公式(11)化简得到公式(12):

k=-(eλ8t-1)b+(eλ5t-1)/137.818

(12)

由公式(12)可知,b和t都是常数,所以k是常数,与初始铅铀比α无关。可见,对于形成时间为t(Ma)的矿物,不同α值的数据在TW图中的投点会形成一条斜率为k的直线,截距为b。由此我们可以得出以下结论:对于含普通铅矿物,如果在体系封闭、无普通铅丢失的情况下,矿物各处经过t(Myr)的演化,其TW图的数据会形成一条倾斜直线。直线方程只与初始铅比值b和矿物年龄t(Ma)有关,与初始铅与铀比值α无关,而线上的理论点(x,y)的具体位置由初始普通铅与现今铀的比例α确定。如图1a所示,在给定初始铅比值b的情况下,不同矿物年龄t(Ma)(如图1a中90、140、250、500Ma)将形成不同的直线,不同的初始铅与现今铀的比例(如图1a中不同颜色等值线所示)控制了理论点其落在TW图中直线的不同位置。

图1 理论模型与数值模拟(a)普通铅与铀比值的理论等值线; (b)单次模拟的各个同位素比值直方分布;(c)模拟数据的TW图分布及拟合结果;(d-f)利用不同分组指标构造的虚拟点及其拟合结果Fig.1 Theoretical models and numerical simulations(a) theoretical contours of the Pbc/U; (b) square distribution of each isotope ratio in one simulation; (c) TW diagram distribution of simulated data and fitting results; (d-f) virtual points constructed with different grouping indicators and their fitting results

1.2 206Pbc/238U的替代指标

由于206Pbc是未知的,因此实验实测数据无法计算获得α值,因为矿物形成时普通铅同位素比值为常数,所以可以利用其他铅同位素代替206Pbc。

204Pbc与238U的比值可以作为α值的替换指标。204Pbc无放射铅干扰,但是204Pbc在普通铅中占比较低,不容易测量,同时由于LA-ICP-MS实验中通入的氦气和氩气中通常含有Hg。204Hg会对204Pbc的测量带来较大干扰。通过测量202Hg可以一定程度上将204Hg干扰剔除。如果待测矿物是黑钨矿,往往会出现186W18O氧化物干扰(Yangetal.,2022);如果待测矿物是独居石和褐帘石,可能会出现232Th144Nd16O双电荷离子干扰(Fletcheretal.,2010; Lietal.,2013)。这些均是204Pbc/238U作为替换指标的不利之处。

除了204Pbc,208Pbc与238U的比值也可以作为α值的替换指标。设普通铅同位素比值206Pbc/208Pbc为γ,普通铅208Pbc与238U比值为z,则α可以利用公式(13)表示:

α=γz

(13)

将公式(13)带入公式(8)中,可得到TW图中各点理论坐标与z的关系,利用公式(14)表示:

(14)

实际情况中,矿物可能含有一定量的232Th,其衰变会带来放射性208Pb*的干扰。为了避免放射性208Pb*带来的影响,利用公式(15)可以由测量数据计算208Pbc/238U:

z=208Pbc/238U=(208Pb-(eλ2t-1)232Th)/238U

(15)

其中,λ2=4.9475×10-5/Myr,代表232Th的放射衰变常数。注意,在以上公式中包含待求的样品年龄t,可以采用预估参考年龄加上迭代的方式进行求解。

2 虚拟点构造方法与模拟验证

2.1 虚拟点构造方法

虚拟点构造方法是通过针对相同z值的数据,构建一个抽样集合,由该集合可以估算一个虚拟点的位置和测量误差。z的值域是非负实数集合,对于矿物面扫描来说只有有限数据,不可能由完全相同的z值构建抽样集合,只能根据z值的相近程度进行抽样构建。为了避免将z值差别较大的数据合并为一个集合,以及避免数据的重复使用,我们可以将面扫描数据按照z值大小进行排序,将每I个相邻数据分组抽取出来,每组数据构建一个虚拟点。这样可以保证集合中I数据的z值彼此相近,这是一种快速构建大量虚拟点数据集合的有效方法(Drostetal.,2018;Chewetal.,2021)。与他们研究不同的是,他们使用的是238U/208Pb和207Pb/235U作为虚拟点的分组指标,而本文经过推导认为208Pbc/238U的比值是最合适的分组指标。

(16)

(17)

抽样集合中测量点越多,期望的统计误差越小,但抽样集合中的测量点数目不能盲目扩大,这会将差异较大z值的数据抽样到一个集合,不满足抽样假设。后文将针对抽样集合大小对定年分析的影响进行数值模拟和讨论。

由公式(16)和(17),我们可以分别计算每个抽样集合的同位素比值238U/206Pb和207Pb/206Pb的期望和误差,并根据集合中的比值测量值计算两者的相关系数,每个抽样集合均可以计算出一个虚拟点,每个虚拟点由5个数据构成。

2.2 数值模拟验证

为例验证以上算法有效性,我们进行了数值模拟。目的在于验证在一定误差干扰下是否可以通过构造虚拟点的方法获得较为准确的交点年龄,同时对比本文提出的分组指标与前人提出分组指标的区别。根据Stacey-Kramers地球演化模型(Stacey and Kramers,1975),假设矿物年龄为t=140Ma,形成时b=207Pbc/206Pbc=0.8848,γ=206Pbc/208Pbc=0.4818。根据年龄可以计算谐和曲线上的定点和截距b,可以确定该矿物在TW图中的理论数据由以下直线模型方程(18)确定:

y=-0.0175x+0.8448

(18)

假设矿物表面现今238U和232Th含量真值在10×10-6～100×10-6之间且服从均匀分布,初始铅占现今铀比值208Pbc/238U真值的对数服从均值为-2,标准差为1的正态分布。可以由随机生成的238U、232Th、208Pbc/238U数据计算出普通铅206Pbc、207Pbc、208Pbc和放射铅206Pb*、207Pb*、208Pb*的真值,进而获得全部铅206Pb、207Pb、208Pb的真值。考虑到利用LA-ICP-MS进行实际测量时,会伴随较大随机噪声,因此对真值数据加入高斯随机噪声,噪声标准差为对应真值的15%,获得206Pb、207Pb、208Pb、232Th和238U模拟测量值。

通过测量数据计算TW图中的238U/206Pb和207Pb/206Pb,以及虚拟点的分组指标238U/208Pb、207Pb/235U和208Pbc/238U,剔除掉其中的无效数据只保留正值数据,共生成5000个测量数据点。

模拟的238U/208Pb和207Pb/206Pb同位素比值数据在TW图中的分布见图1c。由图1c可知,模拟数据分布十分分散,直接利用最小二乘拟合获得直线方程(图1c红色直线):

y=-0.0131x+0.7335

(19)

此时交点年龄122.5Ma与真值140Ma相差较大,可见直接拟合测量点获得方程(19)与真模型方程(18)(图1c蓝色虚线)有较大偏差。普通最小二乘法虽然可以获得最佳的拟合结果,但其前提条件相对严格,当自变量和因变量同时存在均值为零、相同方差的随机误差时,此方法能给出在统计意义上最好的参数拟合结果,当数据不符合其假设时,拟合效果可能会受到影响。TW图的XY变量不满足最小二乘法的基础假设,从而导致计算结果与真实值相差较远。

由散点颜色可知,虽然普通铅与铀的测量值有一定误差,但是仍可以看出分布规律,利用本文提出的抽样构造虚拟点的方法进行分析,有望通过统计方法获得比较准确的拟合方程。

对模拟测量数据按照208Pbc/238U大小排序,按每40个点进行分组,每组内的数据构成一个抽样集合,每个集合均可以构造一个虚拟点,获得125个虚拟点分布(图1f),误差椭圆是根据每40个抽样数据的几何均值的误差和相关系数绘制。由虚拟数据点进行双误差变量线性拟合,获得拟合直线方程(图1f红色直线):

y=-0.0175x+0.8460

(20)

图1f中显示拟合红色直线与真模型方程的蓝色虚线几乎重合,交点年龄为140.2±1.3Ma,与模拟设置的年龄140Ma相一致,截距0.8460与模拟设置的普通铅比值0.8448相一致,其MSWD=0.98,自由度为123,生存概率为55.4%大于5%。

我们利用同一套模拟数据计算了前人研究(Drostetal.,2018)采用其他分组指标的拟合情况。238U/208Pb作为分组指标的虚拟点分布和拟合直线如图1d)所示,每个虚拟点的误差椭圆相对更大,获得拟合直线方程:

y=-0.0175x+0.8356

(21)

图1d中显示红色拟合直线与真模型方程的蓝色虚线几乎重合,交点年龄为141.5±1.6Ma,虽然与模拟设置的年龄140Ma相差不大,但是其MSWD=1.48,自由度为123,生存概率为0%,表明虚拟点到拟合直线的归一化残差分布不满足标准正态分布,残差平方的分布不满足卡方分布。

207Pb/235U作为分组指标的虚拟点分布和拟合直线如图1e所示,由于每个分组内数据的相关性极高,导致虚拟点的误差椭圆呈现为线状,获得拟合直线方程:

y=-0.0175x+0.8507

(22)

图1e中显示红色拟合直线与真模型方程的蓝色虚线几乎重合,交点年龄为139.1±1.3Ma,虽然与模拟设置的年龄140Ma相差不大,但是其MSWD=1.31,自由度为123,生存概率为1.3%同样小于5%,表明虚拟点到拟合直线的归一化残差分布不满足标准正态分布,残差平方的分布不满足卡方分布。

2.3 蒙特卡洛模拟与统计

由于单次模拟具有随机性,所以使用2.2节方法进行1000次蒙特卡洛模拟来评价算法的优劣。根据模拟的1000组数据,分别利用不同指标分组获得了1000组交点年龄和95%年龄误差分布,按交点年龄排序后如图2a-c所示,灰线为95%置信区间,黑色点或红色点代表交点年龄,红色点表明该次模拟获得的年龄置信区间不能涵盖年龄真值,我们将这种情况定义为定年失败,失败次数与模拟总次数1000的比值定义为失败率,238U/208Pb和207Pb/235U作为指标进行定年的失败率分别是24.3%和9.1%,而本文提出的指标失败率为4.7%,与95%置信区间对应的5%失败率相一致。三种分组指标的交点年龄的统计直方图如图2d所示。本文提出的新指标获得的交点年龄为140.1±1.3Ma(2SD),十分接近设定的年龄真值140Ma。前人提出238U/208Pb和207Pb/235U作为指标获得的交点年龄为141.1±1.35Ma和139.4±1.31Ma,这表明在数据分布较好的情况下,这两个指标获得的年龄仍然会系统性偏大或偏小。虽然各个指标的精确度相差不大,但是准确度不够。从平均标准权重偏差(MSWD)这个统计指标来看(图2e),当自由度为123时,显著性水平为5%的单边分布的MSWD拒绝域阈值如图2e红线所示,大于该阈值代表生存概率低于5%,由直方分布可知和207Pb/235U作为分组指标时,MSWD期望分别为1.41和1.52,均高于阈值,而本文提出指标的MSWD期望为1.06远低于阈值。从生存概率分布来看,238U/208Pb和207Pb/235U作为分组指标时,生存概率高于5%的占比只有12.5%和4%,而本文提出指标的生存概率大于5%的占比为85.9%。综合以上分析,不建议以238U/208Pb和207Pb/235U作为虚拟点分组指标,采用208Pbc/238U为分组指标更为有效。

3 面扫描定年分析实验

在实际数据处理时,实验中样品的不同元素/同位素在激光剥蚀和传输中的行为差异,导致进入质谱中分析获得的同位素测量比值与真值存在一定差异,因此需要利用标样估计实验中的不同元素/同位素的分馏系数,然后对测样进行校正,进一步增加了数据分析的复杂度。面扫描定年时含量分析和年龄分析使用的标样是不同的,含量分析需要知道标样各个元素的含量推荐值,而年龄标样需要知道各个同位素比值推荐值。

面扫描分析定年的数据处理流程如图3所示。首先要根据标样计算元素和同位素分馏系数,对测样测量数据进行含量校正和同位素比值校正,获得样品的含量分布和同位素比值分布数据和图像。在测量分析时,如果测样中有包裹体或者穿插岩脉等情况,还需要借助含量分析图像和显微照片图像,先对样品数据进行筛选和提取,在排除干扰后,单独提取定年区域的数据,才能进入定年流程。根据同位素比值数据和由参考年龄校正的分组指标,进行数据分组构建虚拟点,对虚拟点数据进行线性回归获得交点年龄,如果交点年龄与估计的参考年龄不一致,将进入迭代计算,如果在误差范围内一致,则将交点年龄作为样品年龄。

图3 基于LA-ICP-MS面扫描数据的U-Th-Pb定年分析的数据处理流程Fig.3 The data processing flow of U-Th-Pb dating analysis based on LA-ICPMS mapping data

在本文的实验分析中,采用的是GSD-1G作为含量校正的标样,91500作为年龄分析的标样。石榴子石测样ZK803-97来自于长江中下游成矿带鄂东(Edong)矿区铜绿山(Tonglvshan)大型Cu-Fe-Au矽卡岩矿床,对该矿床的综合定年研究表明,该矿床形成时间为139～140Ma(Zhangetal.,2019;Lietal.,2022)。

3.1 实验参数

石榴子石面扫描U-Pb定年实验是在合肥工业大学资源与环境工程学院矿床成因与勘查技术研究中心(OEDC)矿物微区分析实验室完成。激光剥蚀系统使用PhotonMachines Analyte(其中激光器为相干公司193nm ArF准分子激光器),ICP-MS为Agilent 7900。将激光剥蚀系统产生的气溶胶使用氦气(0.9L/min)作为载气,氩气(0.8L/min)作为补偿气以调节灵敏度,二者通过T型混合接口混合,混合气体通过长～1.5m内径为4mm的聚四氟乙烯材质传输管输送至ICP-MS。分析前通过剥蚀NIST SRM 610硅酸盐以获得LA-ICP-MS的最佳灵敏度,238U、232Th的离子信号强度比约为1,ThO+/Th+小于0.2%,尽可能的减少基体效应引起的干扰。实验过程中使用含量标样GSD-1G和年龄标样91500,对石榴子石实验样品ZK803-97进行校正,具体的测量顺序为:GSD-1G、91500、ZK803-97-1、91500、ZK803-97-2、ZK803-97-3、91500、GSD-1G。实验前对样品进行大束斑预剥蚀,降低样品表面铅的干扰,实验过程中激光束斑为30μm,标样和实验样品线扫描剥蚀速度20μm/s,剥蚀频率为7Hz,激光输出能量密度为2J/cm2。剥蚀每个样品前进行20s的背景气体信号采集,剥蚀后吹扫时间20s。

为了同时获得石榴子石的元素含量分布,已知所分析的石榴子石为钙铁榴石的前提下,测试了石榴子石的Si、Ca、Fe等主量元素,通过配氧进行归一化校正。本实验检测元素包括27Al、29Si、44Ca、47Ti、57Fe、206Pb、207Pb、208Pb、232Th、238U,其中27Al、29Si、44Ca、47Ti、57Fe检测时间为5ms,206Pb、207Pb、208Pb检测时间为30ms,232Th、238U检测时间为10ms,死时间为0.33ms,采样周期为0.158s。标样单次线扫描耗时40s,测样单次面扫描耗时5min,累计共耗时15min。

3.2 样品含量分布

石榴子石样品微量元素Al、Ti、Pb、Th、U的分布图像如图4所示。每块石榴子样品的尺寸小于0.5×0.5mm,各种微量元素,特别是与定年分析相关的Pb、Th、U元素分布不均匀。其中,对同一块石榴子石的两次面扫描结果ZK803-97-1和ZK803-97-2含量分布图像十分相近,表明含量分析结果具有可重复性。本文实验只测量了除三种主量元素以外的五种微量元素,其他研究者可以根据实际需要添加其他微量元素进行含量分析。

图4 铜绿山大型Cu-Fe-Au矽卡岩矿床石榴子石样品ZK803-97的微量元素含量分布(a-e)分别为Al、Ti、Pb、Th、U元素的分布图Fig.4 Distribution of trace elements in garnet sample ZK803-97 from Tonglvshan large-scale Cu-Fe-Au skarn deposit(a-e) distribution diagrams of Al, Ti, Pb, Th and U elements, respectively

3.3 样品同位素比值分布

如果年龄标样中不含普通铅,如锆石标样91500,同位素比值有推荐值,可以通过推荐值与测量值之比计算仪器分馏系数,其中同位素比值测量值为多次测量的几何平均值,同时需要估算分馏系数的测量误差合理的传递到年龄分析中。本实验通过对年龄标样91500的三次线扫描,可以获得定年分析实验中所需的分馏系数,在实验过程中分馏系数保持稳定,没有发现分馏系数随时间明显漂移的现象。如果年龄标样含普通铅,则校正方式更加复杂。石榴子石的同位素比值分布如图5所示,其中图5a-c分别是利用91500标样进行分馏系数校正后的238U/206Pb、207Pb/206Pb、232Th/208Pb分布。由于部分区域的206Pb或208Pb测量值低于背景值,导致以0作为分母,同位素比值为无穷大,部分区域232Th和208Pb的测量值低于背景值,导致0比0的情况,显示为黑色,这种情况可以通过提高激光剥蚀频率或束斑加大采样量来避免。锆石91500标样没有232Th/238U和208Pb/238U推荐值,图5d-e显示为未经过校正的测量值。

图5 铜绿山大型Cu-Fe-Au矽卡岩矿床石榴子石样品ZK803-97的同位素比值分布(a-c)分别为经过分馏系数校正的238U/206Pb、207Pb/206Pb、232Th/208Pb的分布图;(d-e)分别为未经过分馏系数校正的232Th/238U和208Pb/238U的分布图Fig.5 Isotopic ratio distributions of ZK803-97 in garnet samples from Tonglvshan large-scale Cu-Fe-Au skarn deposit(a-c) distribution diagrams 238U/206Pb, 207Pb/206Pb and 232Th/208Pb with fractionation coefficient correction, respectively; (d-e) distribution maps of 232Th/238U and 208Pb/238U without fractionation coefficient correction, respectively

3.4 定年区域选择和数据提取

由于本文扫描的石榴子石不含包裹体和岩脉,扫描区域也没有超出样品范围,因此全部区域均可以作为定年区域。否则需要对矿物面扫描后的几个主量元素分布图进行分析,进而对数据进行筛选和提取。此外,为了计算需要,可根据指定阈值对测量数据进行筛选,以避免比值运算中的0作为分母和0的对数运算,以及极少数离群数据的干扰。本文中设置了以下阈值,206Pb>0、207Pb>0、208Pb≥0、238U>0、0<238U/206Pb<150、0<207Pb/206Pb<1.4进行数据筛选,获得的同位素比值数据如图6a-b所示。

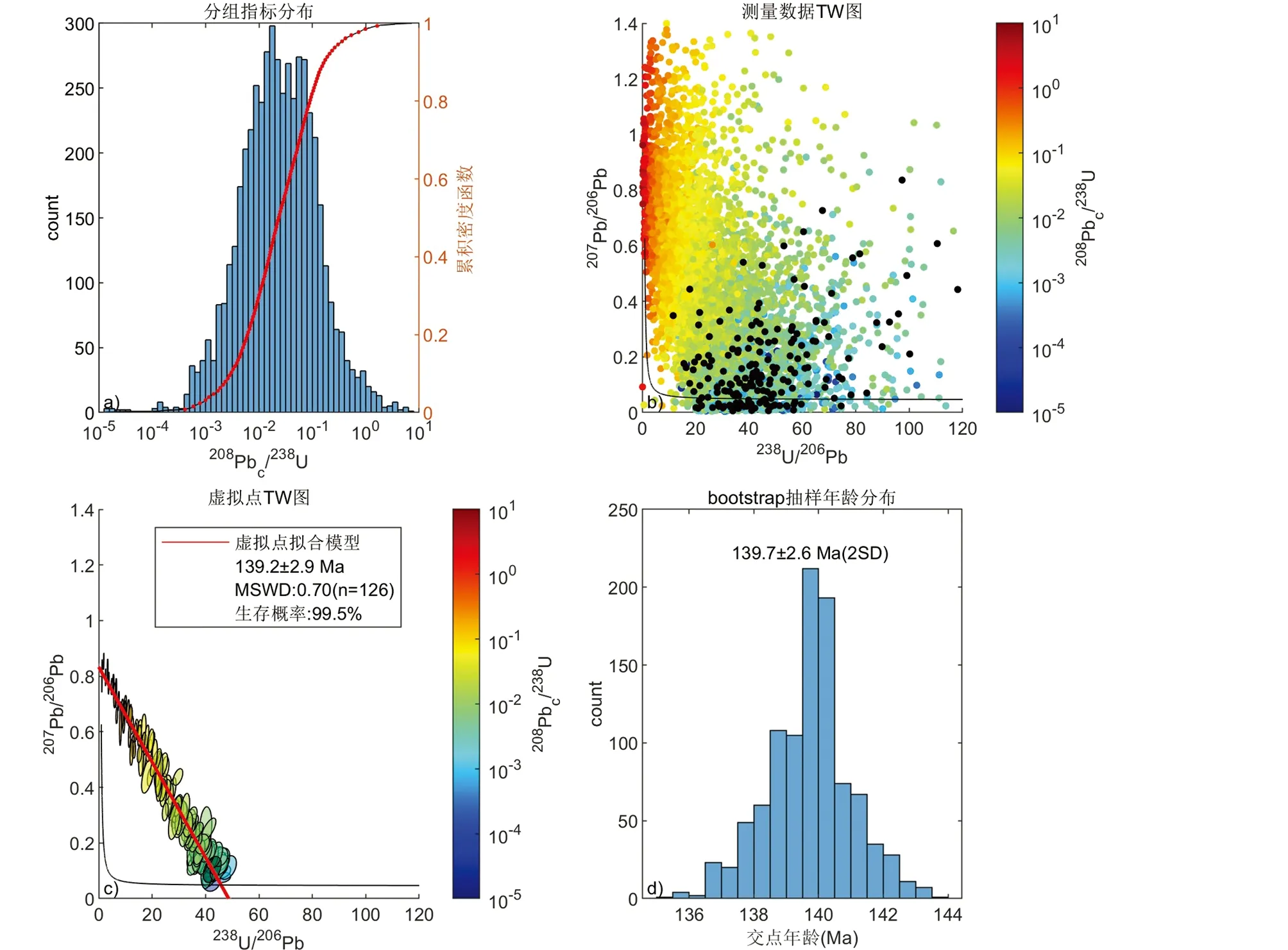
图6 铜绿山大型Cu-Fe-Au矽卡岩矿床石榴子石样品ZK803-97的年龄分析数据分布及结果(a)为校正后分组指标直方分布图;(b)分馏系数校正后的测量数据在TW图中的分布;(c)虚拟点数据在TW图中的分布及拟合结果;(d) 1000次bootstrap模拟获得的交点年龄直方图Fig.6 Age analysis data distribution and results of garnet Sample ZK803-97 from Tonglvshan large-scale Cu-Fe-Au skarn deposit(a) histogram distribution of corrected group indicators; (b) distribution of measured data after fractionation coefficient correction in the TW diagram; (c) distribution and fitting results of virtual point data in the TW diagram; (d) histogram distribution of intersection age obtained from 1000 bootstrap simulations

3.5 测样定年分析

数据分组指标通过公式(23)计算获得:

(23)

其中232Th/208Pb 为分馏系数校正后的数据,208Pb/238U 可以不进行校正,因为不会改变分组指标的相对大小,对排序无影响。

在数值计算时需要考虑0做分母的情况,当出现208Pb测量值为0时,分组指标直接设为0值;当计算结果为负时,意味着由232Th的测量值换算的放射铅大于测量的208Pb总铅,通常是测量误差导致,分组指标也直接设为0值,其数据分布如图6b黑色点所示。

t为样品的推荐年龄,研究者可以预估一个参考年龄进行迭代计算,后文将会分析采用不同初始参考年龄的影响。将提取数据按照分组指标进行排序,通过对每40个点进行抽样分组,根据第2.1节公式,获得虚拟点数据,通过双误差变量线性回归获得回归方程和交点年龄,使用交点年龄替换参考年龄进行1～2次迭代,获得稳定的年龄为139.2Ma。分组指标208Pbc/238U的直方分布如图6a所示,其中累积分布曲线上的每40个点用一个红色点标记分组点位置。TW图中的散点数据分布如图6b所示,其中黑色点为208Pbc校正值小于等于0的数据,彩色点的颜色代表分组指标208Pbc/238U的高低。由散点数据抽样构成126个虚拟点数据如图6c所示。获得的拟合回归模拟与谐和线交点年龄为139.2±2.9Ma (MSWD=0.7,n=126)。

为了避免实验数据分布的随机性对年龄分析误差带来的影响,理论上可以进行多次实验,考虑到实际上无法对一个样品进行几百次面扫描来估计误差水平,这里引入bootstrap方法来根据一次实验数据进行年龄误差的估计(Efron,2000)。对于实验测量的数据进行有放回的抽样,样本大小与测量数据总量一致,每次抽样视为一次独立虚拟实验。通过虚拟点构造、直线拟合和交点计算,每次实验均可以获得一个交点年龄,通过统计该交点年龄的分布可以获得交点年龄点估计的置信区间。我们对标样测量数据和测样测量数据进行1000次bootstrap抽样,用来模拟1000次实验的分析结果,可以获得交点年龄直方分布如图6d所示,其2SD置信区间为139.7±2.6Ma,该分析结果与单次分析年龄139.2±2.9Ma (MSWD=0.7,n=126)相一致。

前人利用LA-ICP-MS点分析方法以石榴子石样品PL57作为标样,分析铜绿山石榴子石样品,获得的年龄为139.2±3.4 Ma (MSWD=1.8,n=18)(Lietal.,2022)。前人利用LA-ICP-MS点分析方法以锆石91500作为标样,对ZK803-97样品的年龄分析结果分别为:139.1±1.0Ma (MSWD=0.79,n=38)、139.8±2.6Ma(MSWD=0.48,n=26)、143.4±8.3Ma(MSWD=2.3,n=31)(Zhangetal.,2019)。由此可以见,本文利用面扫描方法获得了远多于点分析获得的数据量,获得的年龄与前人研究结果相一致。

4 讨论与结论

4.1 分馏系数对定年的结果影响

分馏系数的确定通常对定年分析有直接的影响,我们通过固定其他分馏系数,变化一种分馏系数进行定年分析,来评估不同分馏系数测量的不确定性对ZK803-97样品定年结果的影响程度。由图7a-c所示,不同同位素分馏系数对ZK803-97样品的年龄带来的影响是有差异的,238U/206Pb分馏系数对定年分析的影响最大,而232Th/208Pb分馏系数影响最小,238U/206Pb分馏系数增加0.05,交点年龄减小约9Ma;207Pb/206Pb分馏系数增加0.05,交点年龄减少约0.45Ma;232Th/208Pb分馏系数变化导致交点年龄波动的幅度可以忽略。通常在定年分析中,往往不考虑分馏系数的误差,在本次研究中,由91500标样计算获得的238U/206Pb分馏系数期望及其误差为0.780±0.009,95%置信区间宽度为0.018,分馏系数测量不准确可能导致的年龄偏差约3.2Ma;207Pb/206Pb分馏系数期望及其误差为1.013±0.018,95%置信区间宽度为0.036,分馏系数测量不准确可能导致的年龄偏差约0.32Ma;232Th/208Pb分馏系数期望及其误差为0.975±0.015,95%置信区间宽度为0.030,年龄偏差可忽略不计。面扫描定年对仪器的稳定性有较高要求,如果在实验过程中,发现标样的分馏系数出现明显的仪器漂移,则需要进行分段漂移校正,如果无法准确计算元素分馏系数,将对定年分析准确度产生严重影响。

图7 铜绿山大型Cu-Fe-Au矽卡岩矿床石榴子石样品ZK803-97样品的参数敏感性分析(a-c)分别为不同分馏系数对定年结果的影响;(d)不同起始参考年龄对交点年龄的影响;(e、f)不同抽样样本大小对MSWD和交点年龄的影响Fig.7 Parameter sensitivity analysis of garnet Sample ZK803-97 from Tonglvshan large-scale Cu-Fe-Au skarn deposit(a-c) the influences of different fractionation coefficients on the dating results of ZK803-97 Sample; (d) the effects of different initial reference ages on the intersection age; (e, f) the effects of different grouping sizes on the MSWD and intersection age

4.2 基体不匹配的影响

锆石标样91500基体与测样石榴子石存在基体不匹配的问题,可能导致系统性偏差。虽然我们的结果与前人的结果是一致的,但是仍然不能排除系统性偏差。通过改进实验仪器、调节仪器实验参数、加入特殊气体,可以大大减少基体不匹配的影响,但是上述方法仍然受到多方面约束,限制较大。只有使用基体匹配的不含普通铅或含普通铅极低的均匀样品作为标样才能避免产生这种系统性偏差,但是这种标样一般较为稀少,不易获得。因此利用同基体的样品进行分馏系数校正的面扫描定年方法可能更具有实用性。本文认为如果利用通过其他高精度分析方法获得了含普通铅样品的准确年龄,该样品理论上也可以成为标样,通过面扫描虚拟点分析,也可以确定分馏系数,进而校正基体相同但年龄未知的样品。该方法如果开发成功,可以大大减少对标样选择的限制,解决基体问题带来的偏差。

4.3 起始参考年龄的影响

由于确定分组指标需要先扣除208Pb*,且在分析之前不知道样品的年龄,因此需要先假设一个参考年龄进行分析,再由交点年龄代替参考年龄进行迭代分析。我们分析了不同起始参考年龄对ZK803-97样品定年分析的影响,由图7d可知,无论选择什么参考年龄,均可以快速收敛,并在1～3次迭代内收敛到样品年龄,因此,起始参考年龄的具体数值的选择不重要,不会对定年分析结果造成影响。

4.4 虚拟点抽样样本集合的大小的影响

在虚拟点构造时,本文指定了抽样样本集合大小为40,为了分析样本集合大小对定年的影响,本文尝试用不同大小的样本集合进行分析。由图7e可知,抽样集合大小在20～200之间时,MSWD均小于1,说明产生的定年数据满足统计规律。由图7f可知,定年结果的交点年龄在误差范围内是重叠的,并且均包含了前人认为139～140Ma这个年龄区间。因此,我们认为抽样样品集合大小对定年的影响较小。

4.5 研究展望

本文开发了一种新的基于LA-ICP-MS面扫描技术U-Th-Pb定年方法,并成功应用于矽卡岩矿物中石榴石的U-Pb定年。该方法不仅适用于矽卡岩中石榴子石定年,也同样适用于符山石、绿帘石等含U矿物的定年,从而约束矿床热液过程的精确年龄。该方法将对我国新一轮关键矿产、关键金属成矿研究提供有力支持。我们将继续研究相关技术方法,争取利用数据分析手段解决副矿物U-Pb定年标样稀缺问题。同时,我们将积极开发配套软件,匹配显微图片技术,争取实现对样品的不同区域数据的分别提取,对矿物核心、环带以及穿插岩脉分别分析处理,为矽卡岩型相关关键金属矿床的研究提供更为便捷的手段。

4.6 结论

本文从理论推导、模拟数据分析、处理流程设计、实验分析、参数敏感性讨论等方面对含普通铅矿物LA-ICP-MS面扫描定年技术进行了论述。使用本技术方法对已知年龄石榴子石样品ZK803-97进行面扫描分析,通过15min的面扫描同时获得了含量结果和年龄结果,分析年龄与前人文献报道的矿床年龄相一致,验证了方法的有效性,本文得出以下结论:

(1)LA-ICP-MS面扫描分析可以同时获得高分辨率元素空间信息和样品的年代学信息,无需再次选点进行点分析定年,降低了分析成本和操作难度,同时避免了点分析选点问题和深度分馏问题,提高了分析效率。

(2)通过同时测量206Pb、207Pb、208Pb、232Th和238U数据并进行数据联合分析,以校正后的208Pbc/238U作为分组指标重新抽样构建虚拟点,是含普通铅样品定年分析的有效方案。

(3)在各种影响因素中,238U/206Pb分馏系数的准确性对定年分析的影响最大,实验中需要保证仪器状态稳定,并且需要选择合适的标样进行分析,标准样品和待测样的分馏系数不一致将会带来系统性偏差。