基于数学核心素养之“数学抽象”下的初中数学解题教学策略——以“探索三角形全等条件”为例

唐 丽

(连云港市和安中学,江苏 连云港 222006)

《义务教育数学课程标准(2022年版)》确立了核心素养导向的课程目标,旨在通过数学学习,培养学生运用数学眼光观察现实世界、运用数学思维思考现实世界、运用数学语言表达现实世界的素养.数学抽象是数学核心素养的重要组成部分,是学生理解数学知识、提炼数学问题、解决数学问题的关键.可以说,数学抽象素养是学生学习数学的关键,也是学生运用数学知识解决实际问题的基础.在教学实践中,受传统教育观念的影响,教师将大量时间和精力集中在数学知识和解题技巧训练方面,忽视了数学抽象素养和解题之间的关系,弱化了思考、辨析过程,导致学生难以理解数学问题本质,无法从根本上提升学生的数学解题能力.为此,初中数学教师需认真学习新课程理念,立足数学抽象素养和解题的内在联系,优化和完善解题教学模式,探索和改进初中数学解题教学策略,提升解题教学效果,不断提升学生的数学解题能力.

1 数学抽象与数学解题教学概述

初中阶段,核心素养主要表现为:抽象能力、运算能力、几何直观、空间观念、推理能力、数据观念、模型观念、应用意识、创新意识.数学抽象作为数学核心素养的重要组成部分,是引领学生解题的基础和关键.顾名思义,数学抽象是一种思维过程,主要是将共同、本质的特征从事物中抽象出来,并将非本质性的特性舍去.数学抽象是数学研究过程中的一个思维过程,借助必要的数学抽象素养,通过层层抽象,可以精准把握数学问题的本质,进而抓住解决数学问题的关键.另外,在新课程理念下,数学问题日渐生活化,赋予了数学问题的生活背景,其中存在一定的干扰信息.鉴于此,学生在解决这一类数学问题时,必须要具备极强的数学抽象素养,才能将数学问题从中抽象出来,进而运用所学的数学知识进行分析和解决[1].可以说,在初中数学学习中,学生的数学抽象素养直接影响了其解题能力.

2 基于“探索三角形全等条件”探索数学抽象下的解题教学策略

2.1 融入数学思想解决问题

数学思想实际上是一种数学思维,是思考数学问题时的一种思路,是学生进行数学学习的前提,也是解决数学问题的重要条件.因此,鉴于数学抽象和数学解题的内涵,在引领学生进行解题时,应全面加强数学思想的渗透[2].

例1如图1,已知△ABC中,AB=AC,D为AB上一点,E为AC延长线上一点,连接DE,交BC于点G,DG=EG.求证:BD=CE.

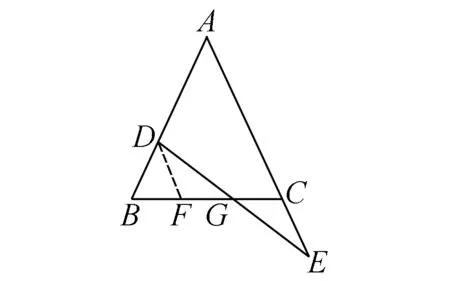
图1 例1题图

分析根据图形特征,需借助全等三角形的性质证明BD=CE.基于此,应充分利用数学转化思想,通过构造全等三角形解决问题.

证明如图1,过点D作DF∥AE,交BC于点F.

易知∠E=∠FDE,∠DGF=∠EGC.又因为DG=EG,所以△DFG≌△ECG,所以CE=DF.因为DF∥AE,所以∠ACB=∠DFB.又因为AB=AC,所以∠ABC=∠ACB,所以∠ABC=∠DFB,所以DB=DF.又因为CE=DF,所以BD=CE.

2.2 巧妙添加辅助线解题

在解决与全等三角形相关问题时,很多题目中并未直接给出三角形,给解题带来了极大的难度.为此,在数学解题教学中,应指导学生巧妙添加辅助线,构造全等三角形,为问题解决创造条件.

例2如图2,在△ABC中,AC=5,AB=7,求△ABC中线OA的取值范围.

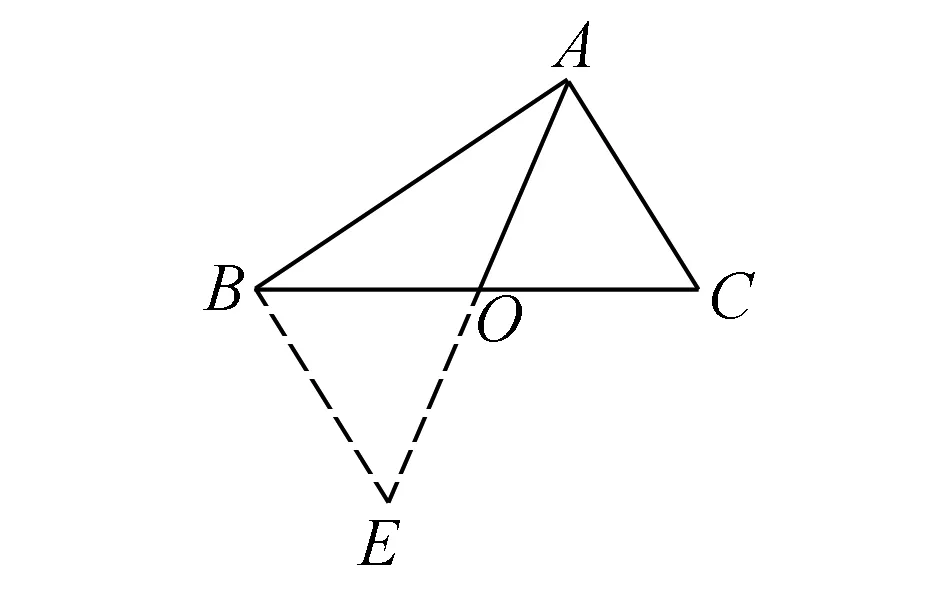
图2 例2题图

分析根据已知条件及所求结论,需借助辅助线将线段AC,AB,OA转化到一个三角形中,使其分别为三角形的三边,然后利用三角形全等、三角形三边之间的关系解决问题.

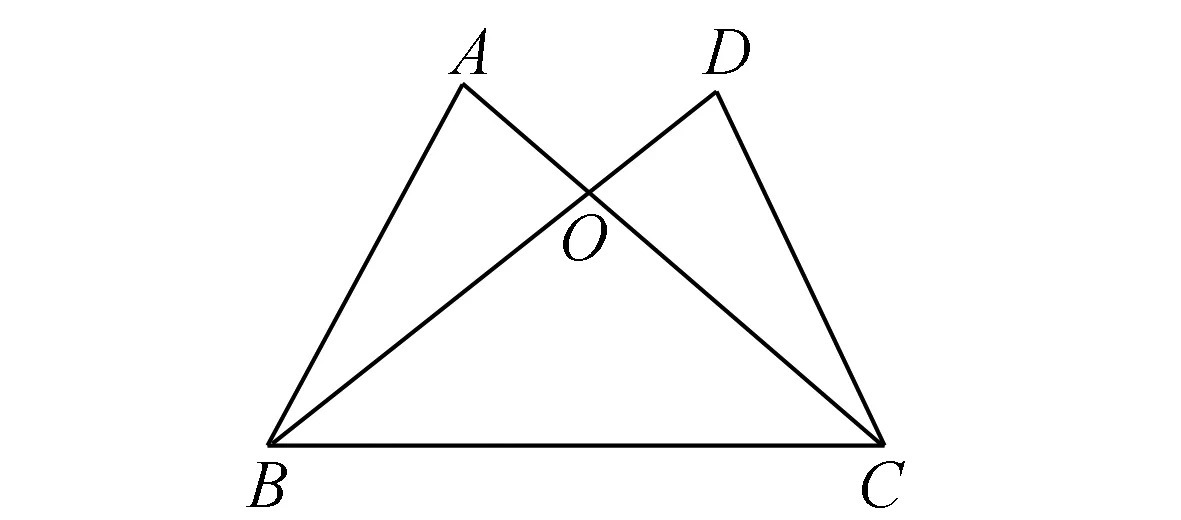
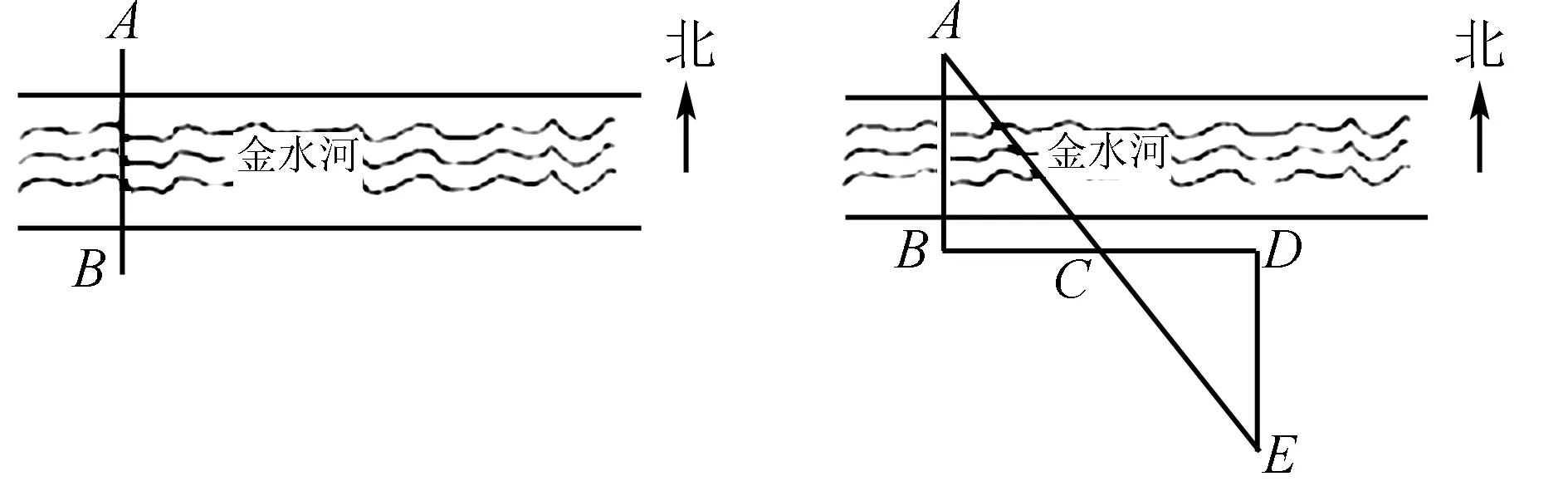
解如图2,延长AO到E,使OE=OA,连接BE.易知△AOC≌△EOB,所以AC=BE.在△ABE中,AB-BE

2.3 加强数学思维训练

数学学科素有“思维体操”的美称,极具逻辑性和抽象性,对学生的思维水平要求比较高.尤其是在解题教学中,解题教学模式固化,弱化了学生解题思维.在这种解题教学模式下,难以真正提升学生的数学解题能力.为此,在数学解题教学中,教师应立足学生在数学解题中面临的“思维黑洞”,结合不同的题目,借助不同的方式,对学生展开思维训练.

例3如图3,AB=DC,AC=DB,AC与DB相交于O点.求证:∠A=∠D.

图3 例3题图

分析针对这一题目,学生只要结合三角形全等判定条件,即可完成题目的高效解答.在具体的解题教学实践中,为了培养学生的数学抽象思维能力,切实提升学生的数学解题能力,教师应以此题为中心,对学生开展变式训练.

变式1去掉图3中的线段BC,其他条件不变,据此提出问题:∠A和∠D是否相等?

变式2改变题目中所求结论,引导学生思考:如图3,已知AB=DC,AC=DB,求证:∠ABD=∠ACD.

变式3改变题目中所求结论,引导学生思考:如图3,已知AB=DC,AC=DB,求证:AD∥BC.

针对变式训练,教师引导学生多角度思考,加深学生对三角形全等判定条件的认识,不仅增强了学生的学习效果,也促进了学生数学抽象素养的发展,提升了学生的数学核心素养,为提升学生的解题能力奠定了坚实的基础[3].

2.4 强化数学符号转化训练

在初中阶段,新课程标准不仅要求学生学会具体知识,更要求学生掌握知识的本质,能够运用数学知识和数学模型分析与解决生活中的问题.为此,初中数学教师必须树立“生活即教育”的观念,立足数学知识和实际生活的内在联系,带领学生从数学学习拓展到实际生活,引领学生在生活化的数学学习中促进数学知识迁移和应用能力的发展.在解题教学中,教师应强化学生的数学符号转化能力训练,使学生能够从实际生活中抽象出数学问题,并运用所学的数学知识进行解答.

例4金水河河道有一段平行的两岸,如图4所示.数学学习小组利用课余时间进行距离测量:数学小组在河道的南岸选择了一棵树B,观察到河对岸正对着B处有一个灯柱A,他们设计了若干个测量方案.请你运用所学的知识,设计出一种无需过河即可测量出A,B两点之间距离的方案,并说明理由.

图4 例4题图 图5 例4测量方案图

分析本题极具生活化,将“三角形全等条件”的相关知识和实际生活结合在一起.解答本题时,学生不仅要具备扎实的基础知识,还应具备极强的数学抽象能力,从实际问题中抽象出数学问题,并提出具体的解决方案.

解如图5,从点B出发,沿着河边向东走至点C,在此处插上标杆之后,继续向东走至点D,使得CD=BC,然后以点D为起点向南走至点E,使A,C,E三点处于同一条直线上.此时,即可通过测量线段DE的长度而得出线段AB的长度,此即A,B两点之间的距离.理由如下:

在△ABC和△EDC中,

因为∠B=∠EDC,∠ACB=∠ECD,BC=DC,

所以△ABC≌△EDC,即AB=DE.

2.5 强化学生数学审题能力

正所谓“工欲善其事必先利其器”,学生唯有具备极强的审题能力,才能理解题目的内涵,理清题目中的数量关系,并由此形成明确的解题思路.在新课程理念下,初中数学问题考查方式发生了变化,呈现出了全新的特点,对初中生的数学审题能力提出了更高的要求.为此,为强化学生的数学抽象能力,培养其解题能力,教师应重视培养学生的数学审题能力.一方面,教师应指导学生在日常审题中认真阅读题目,仔细分析已知条件,并借助圈点的方式,找出关键词.还应深层次剖析,挖掘题目中的隐含条件,剔除迷惑性的条件,寻找数学问题的本质;另一方面,鉴于数学审题的要求及学生数学审题能力现状,教师还应借助一定的数学工具,并通过系统化的训练,使学生逐步形成一定的审题能力[4].

综上所述,新课程理念下,发展初中学生的数学抽象素养,提升学生的数学解题能力,已经成为数学教学的重中之重.在初中数学教学中,教师唯有改变传统数学解题教学模式,立足数学抽象和解题之间的内在联系,并据此开展针对性训练,从而强化学生的数学抽象素养,提升学生的解题能力.