妙用质心巧解高考压轴题

程志强

(山东省济钢高级中学 山东 济南 250100)

1 质心知识回顾

设N个质点系统中各个质点的位置分别为x1、x2、x3、…、xN,我们定义此质点系的质心位置xc为

质心速度为

质心加速度为

系统的合动量是质心的动量

系统的牛顿第二定律可以写成

F=Mac

此式告诉我们:质心的运动行为可以代替质点组的运动行为,质点组的质量等于质心的质量,作用在此质心的力等于系统所受到的外力矢量总和.这个结论称为系统的质心运动定理[1-2].

质心运动定理表明,牛顿定律具有一种独特的性质,即如果它在某一小尺度范围内是正确的,那么在大尺度范围内也将是正确的.鉴于此,实验室中证实质点运动规律的一切实验,利用多质点系统(例如小球)去实现才成为可能.在解决有多个物体相互作用的问题时,如果在质心系中解决问题,会给人以柳暗花明又一春的感觉,会将很复杂的问题变得十分简单[3],将压轴题快速破解.

2 应用比较

2.1 巧解高考压轴题1

【例1】(2014年高考安徽理综卷第22题)在光滑水平地面上有一凹槽A,中央放一小物块B.物块与左右两边槽壁的距离如图1所示,L为1.0 m,凹槽与物块的质量均为m,两者之间的动摩擦因数μ=0.05,开始时物块静止,凹槽以v0=5 m/s初速度向右运动,设物块与凹槽槽壁碰撞过程中没有能量损失,且碰撞时间不计,g取10 m/s2,求:

图1 物体与凹槽位置图

(1) 物块与凹槽相对静止时的共同速度;

(2) 从凹槽开始运动到两者相对静止物块与右侧槽壁碰撞的次数;

(3) 从凹槽开始运动到两者刚相对静止所经历的时间及该时间内凹槽运动的位移大小.

方法1：一般解法

解：(1)B在A中左右运动,与左右边碰撞及两者间摩擦力都是内力,系统动量守恒,最后达到共同速度,由动量守恒得

mv0=2mv1

解得

(2)A和B间的滑动摩擦力f=μmg,系统动能的减少等于产生的热量,即

代入数据得

s相对=12.5 m

考虑到L=1 m,物块最后停在凹槽左侧,两者达到共同速度,物块与前边碰撞6次.设A、B碰前的速度分别为v1、v2,碰撞后的速度分别为v′1、v′2,因为是弹性碰撞,所以

m1v1+m2v2=m1v′1+m2v′2

m1=m2

解得

v′1=v2v′2=v1

即A、B两个物体不断碰撞,每碰一次两者交换速度一次,以地面为参考系画出两者的v-t图像,由于加速度大小都为μg,图像具有对称性,且两者图像不断转换,根据碰撞次数可以分成13段,如图2所示.

图2 物体与凹槽碰撞速度时间图

对凹槽

所以

t=5 s

凹槽的v-t图像与时间轴所围面积即为凹槽的位移,也就是图中阴影的面积,上面等腰三角形面积被分割成13份,第一份阴影面积0.5L,其余均为L.

由以上解法可知:本题难在两个物体的不断碰撞,不断交换速度,过程复杂,即使借用图像也不易画对,面积也不易算对,本题是典型的压轴难题.

方法2：在质心系中的解法

(1)设A和B的质量均为m,由于系统不受水平方向外力作用,因此系统水平方向动量守恒.系统动量为2mvc,其中质心速度vc等于A和B相对静止时的共同速度.由动量守恒可求得

A和B间的相对运动分析:第一阶段,B从A中央右行,B受摩擦力加速,A受摩擦力减速,A快于B;第二阶段,B与A左端互碰,交换速度(弹性碰撞,A和B质量又相等),A以B碰前的速度运动,并受摩擦力加速,B以A碰前的速度运动,并受摩擦力减速.因此,可以认为B由第一阶段的加速运动,在第二阶段中被A取代.如此继续下去,直至A和B相对静止,以共同的质心速度向右前进.

从以上分析,就B相对A运动的相对路程可以等价地看成B在足够长的A内运动,直至相对静止为止,设所经历的路程为s相.

因为作为一对作用力和反作用力的摩擦力做功的大小等于摩擦力与相对路程的乘积

Af=-μmgs相

根据动能定理

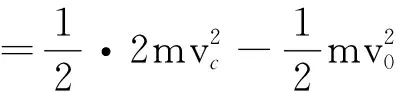
由于s相是B相对A运动的相对路程,所以B可与A碰撞12次(L=1.0 m),最后停在箱A与右壁接触处(只接触,不碰撞).

(2)为考查从B开始运动到A和B相对静止经历的时间,仍然采用上面的等价法,即B在足够长的A内运动.

仍采用这种等价法,以物体B 为研究对象,采用动量定理,求出A和B 相对运动经历的时间,即

-μmgt=mvc-mv0

解得

(3)因过程中系统质心速度vc不变,质心位移为

又因初态时系统质心在A中央,末态时B相对A静止在A左侧,系统质心在凹槽中点左侧0.25 m处,位置图如图3所示,所以A的位移(以A中央处为代表)为

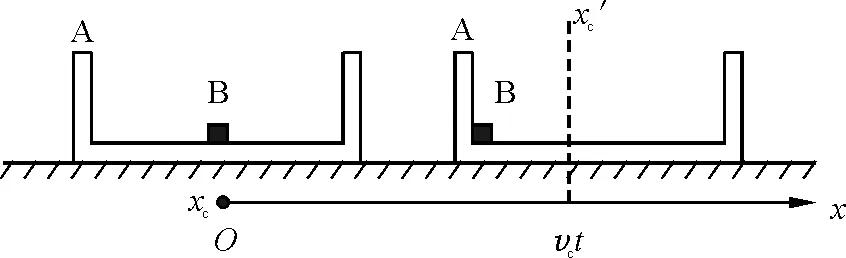
图3 碰撞前后物体与凹槽位置图

xA=xc+0.25 m=12.75 m

可以看出:利用系统质心概念避免了复杂的计算,方便简洁.

2.2 巧解高考压轴题2

【例2】(2015年高考安徽理综卷第12题)由3颗星体构成的系统,忽略其他星体对它们的作用,存在着一种运动形式:3颗星体在相互之间的万有引力作用下,分别位于等边三角形的3个顶点上,绕某一共同的圆心O在三角形所在的平面内做相同角速度的圆周运动(图4所示为A、B、C3颗星体质量不相同时的一般情况)．若A星体质量为2m,B、C两星体的质量均为m,三角形的边长为a,求:

图4 三星转动位置图

(1)A星体所受合力大小FA;

(2)B星体所受合力大小FB;

(3)C星体的轨道半径RC;

(4)三星体做圆周运动的周期T．

方法1：一般解法

分析:3个星体分布在等边三角形顶点上,可以求出相互间的万有引力,夹角成60°,可以用余弦定理求得合力,B与C是对称的,共同圆心应在B、C连线中垂线上.

(1)由万有引力定律,写出三星体间的万有引力

(1)

(2)

(3)

根据余玄定理

(2)同上,B星受到的A、C施加的万有引力分别为

(4)

(5)

根据余玄定理

(6)

(3)如图5所示,△ABC为等边三角形,边长为a,通过对B的受力分析可知,合力的方向经过BC的中垂线AD的一点,记作O点,所以3个圆的圆心O一定在BC的中垂线AD上,从D点做AB的平行线交BO延长线于P,连接AP.

图5 三星受力分析图

由图5中的几何关系可得

由式(4)、(5)得

即

DP=2BD=a(D为中点)

由图5中的几何关系同理可得

即

故O为平行四边形的对角线的中点.由图得

(4)由题可知C的受力大小与B的受力相同,对C星

整理得

方法2:利用质心概念,结合对称性

因为系统不受外力,质心加速度、速度都为零,3个星体将绕质心做匀速圆周运动,系统质心一定在BC边垂线AD的中点上,即图中的O点,A、B、C3个星体转动的半径分别是OA、OB、OC,如图6所示.

(1)根据对称性知∠BAD=30°,A星体受到B、C的万有引力的合力为

FA=FBAcos 30°+FCAcos 30°=

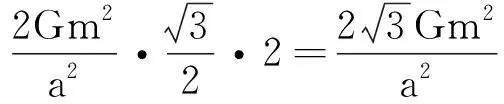
(2)由图可知

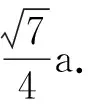
(4)对A有

解得

可以看出:在上面的解法中,利用质心概念快速解出3个星体转动的共同圆心,进而解出运动半径,很快将所有问题方便地解出.

3 总结

质心概念在物体系中是非常重要的概念,在一些高考题,尤其强基计划考试和物理竞赛中如果在质心系中解决问题,在宏观上进行研究,将对问题大大地简化,避免了复杂的过程运算,起到意想不到的效果.

下面看一道清华大学某年自主招生题.

【试题】质量相同的两个小球,质量都是m,用长2L轻绳相互连接,然后静止放在光滑水平面上,绳处于伸直状态,如图7所示,现在用恒力F作用于绳的中央,F方向水平,并且垂直于绳的初始长度方向,两球从静止开始运动.试问:在两球第一次相碰前的瞬间,小球在垂直于F作用线方向上的分速度v⊥的值为多大?

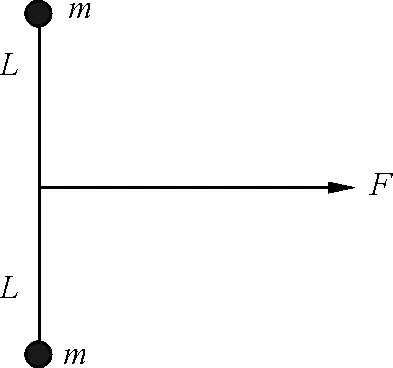
图7 清华自由招生试题附图

方法1:在质心系中求解

应用动能定理,F相对质心做功W=FL.每个小球相对质心碰撞前的速度为v⊥,根据质心系的动能定理

所以

方法2:在桌面参考系中求解

设小球在桌面上运动了s距离小球即将相碰,速度沿绳方向分量为vx,垂直于绳方向分量为v⊥,根据动能定理

对其中一个小球水平方向应用牛顿二定律

联立以上几式得

显然:利用质心系解决问题,更方便、更简洁.