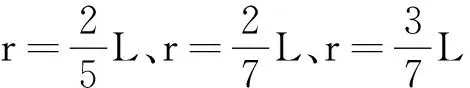带电粒子在等边三角形分界匀强磁场中周期性运动轨迹分析*
李 峥
(重庆求精中学 重庆 400015)
黄海洋
(复旦大学自然科学试验班 上海 200433)
1 问题的提出
带电粒子在匀强磁场中的运动往往涉及圆心、半径及运动时间的确定,通常的解题思路为根据速度方向或入射点、出射点的情况确定圆心,根据圆心确定运动轨迹,根据几何关系确定半径,根据偏转的圆心角确定运动时间.由于带电粒子在磁场中运动的约束条件,其运动往往具有对称性和周期性[1].
【例题】如图1所示,边长为L的等边三角形ABC内、外分布着两方向相反的匀强磁场,三角形内磁场方向垂直纸面向外,两磁场的磁感应强度大小均为B[2].顶点A处有一粒子源,粒子源能沿∠BAC的角平分线发射不同速率的粒子,粒子质量均为m、电荷量均为+q,不计粒子重力及粒子间的相互作用力,则发射速度v0为哪一值时粒子能通过B点( )

图1 例题情境图
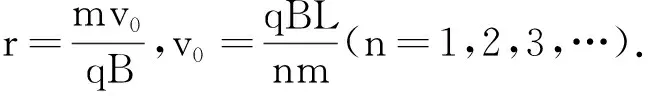
粒子通过B点以后在洛伦兹力的作用下将继续运动,那么具体的情况又如何呢?笔者对粒子运动情况及运动轨迹做了初步的分析.
2 粒子的运动轨迹分析
2.1 从A点出发的带电粒子轨迹分析
通过分析计算,笔者发现通过B点的粒子经过一定时间后均能回到A点,利用GeoGebra作出其运动的轨迹,分别如图2至图9所示.

图2 r=L的粒子轨迹

图3的粒子轨迹

图4的粒子轨迹

图5的粒子轨迹
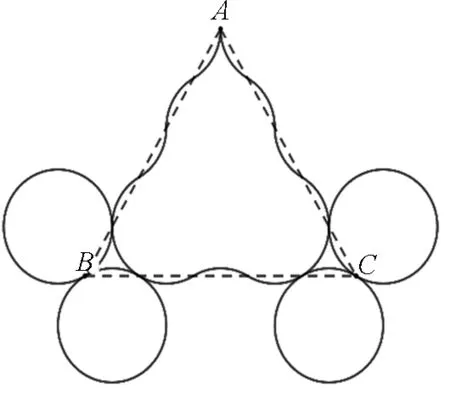
图6的粒子轨迹

图7的粒子轨迹

图8的粒子轨迹
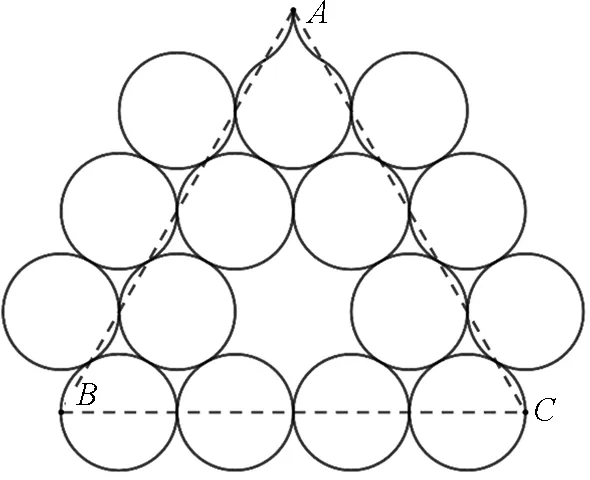
图9的粒子轨迹
通过运动轨迹分析,我们可以初步得到以下结论:
(1)所有通过B点的带电粒子之后的运动轨迹一定过A点.
(2)所有的运动轨迹都是关于过入射点A点的竖直轴线轴对称.
(3)所有的运动轨迹在从A点出发到回到A点的过程中不重复.
(4)粒子回到A点时速度方向与入射速度方向相反.
进一步讨论分析,我们发现其运动时间及对应的路程存在以下的递推关系:
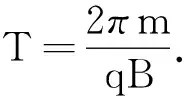
(1)当n=2k+1(k=0,1,2,3,…)时,对应的运动时间
即
将n=2k+1(k=0,1,2,3,…)代入得

整理可得
(2)当n=2k(k=1,2,3,…)时,对应的运动时间
即
整理可得
对应的运动路程
整理可得

综上可得
带电粒子回到A点之后会继续运动且具有周期性,其完整的运动情况又如何呢?笔者通过分析,作出了该情况下对应轨迹,如图10至图17所示.

图10 r=L的粒子轨迹
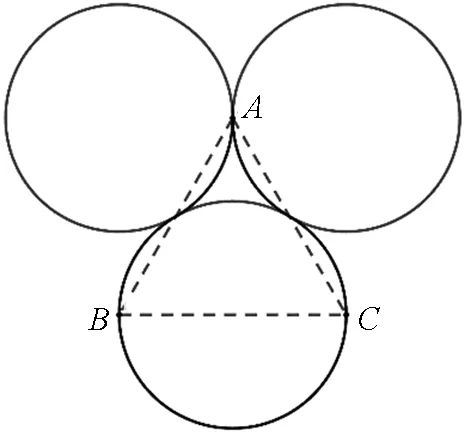
图11的粒子轨迹

图12的粒子轨迹

图13的粒子轨迹

图14的粒子轨迹
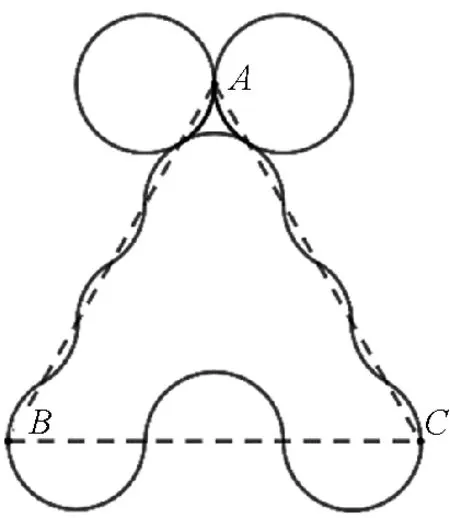
图15的粒子轨迹

图16的粒子轨迹

图17的粒子轨迹

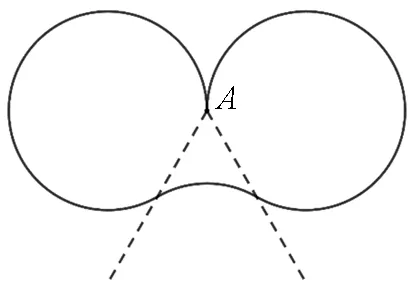
图18 与回到A点相比轨迹增加部分
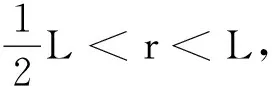

图19 时的完整运动轨迹
2.2 从BC中点出发的带电粒子轨迹分析
若带电粒子从BC中点垂直于边界进入三角形磁场,那么运动情况又如何呢?



图20 的粒子轨迹
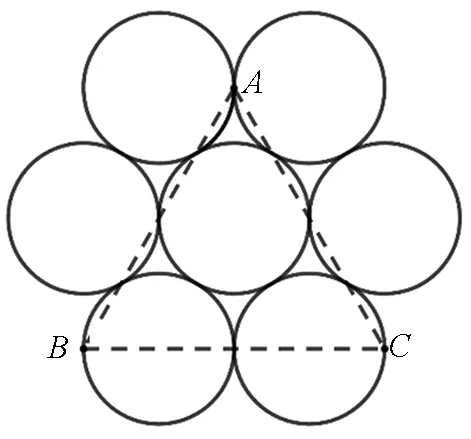
图21 的粒子轨迹
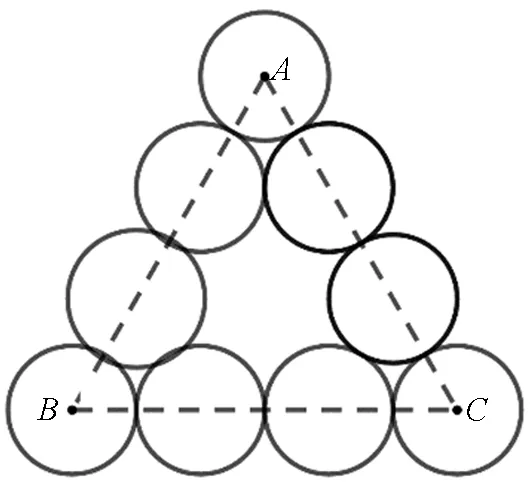
图22 的粒子轨迹
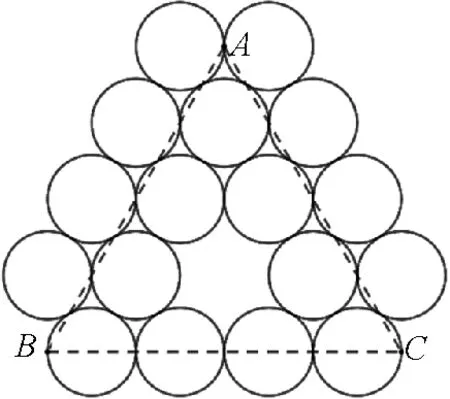
图23 的粒子轨迹

图24 的粒子轨迹

图25 的粒子轨迹
通过分析,轨迹具有以下特点:
(1)运动轨迹具有高度的对称性,且运动具有周期性.

(3)设其运动的周期为T0,则
3 结束语
带电粒子在匀强磁场中的周期性运动通常可以利用对称性进行分析和求解,特别是针对分界磁场,通过计算在某边界两边的运动时间,通过对称性找到对应的总时间,但这个过程中需要特别注意其具有轴对称还是中心对称的性质.其运动的周期通常可以采用单边界两侧运动时间乘以对应边数,再减去重复情况进行处理.