利用节点传播熵识别超网络重要节点

吴英晗，田 阔，李明达，胡 枫

1.青海师范大学 计算机学院，青海 810008

2.藏语智能信息处理及应用国家重点实验室，青海 810008

3.高原科学与可持续发展研究院，青海 810008

网络科学的蓬勃发展使得复杂网络的研究成为诸多领域关注的热点。重要节点识别作为分析与理解复杂网络特性、结构、功能的有效方式之一，被广泛地研究并应用。例如，通过对新冠病毒传播网络中的超级传播者实施隔离，能够大幅度降低病毒的传播速度，进而抑制病毒的扩散；通过对社会网络中舆论领袖的言论加以控制，能够有效抑制或促进信息的传播；通过对交通网络中重要的枢纽站点进行维保，能保证整个交通网络正常运行的稳定性和流畅性。由此可见，识别网络中的重要节点具有重大的应用意义。

由于现实世界是由多种主体关系组成的复杂系统，不同系统结构在网络中表现为节点与边的异质性[1]。在某些情况下，基于普通图的复杂网络[2-3]不能完全刻画真实世界的网络特征，因而，人们便将研究的视角转向基于超图的超网络[4-8]。目前，研究人员根据不同的实际需求提出了众多超网络重要节点识别方法。其中，超度[7]是评估网络节点重要性的常用方法，该方法有效但不精准；介数中心性[8]和接近中心性[8]考虑节点间的最短路径数量和平均最短距离，此类方法从网络全局角度出发，效果明显但时间复杂度较高，不适用于大规模超网络；K-shell分解法[9]考虑节点在网络中的位置信息，计算时间复杂度低，适用于大型网络，但其划分结果过于粗粒化。为了改善结果粗粒化的情况，周丽娜等[10]基于复合参数的思想，结合超度及K-shell 值利用欧氏距离公式提出了一种超网络关键节点识别方法。Son等[11]基于转录组学数据构建超图，引入新的平均超图中心性指标对与病毒/病原体感染相关的基因集进行对比分析，结果表明平均调和s-介数中心性能够有效识别关键基因。Kovalenko 等[12]用向量表示超图中节点的重要性，并据此揭示了同一节点在不同阶数的交互关系中所扮演的不同角色；Aktas等[13]基于扩散模型，提出了两种新的超图拉普拉斯算子用以识别超图中重要的超边，并通过与一般中心性指标对比分析了新方法的性能优势；Xie等[14]运用超图上的传播动力学过程提出了一种基于节点适应度消减的影响力最大化算法，揭示了超图中节点间的高影响力重叠现象与节点度、超度间的强相关性。Lai 等[15]选取不同类型的交通网络为对象，采用节点度、邻居节点度、加权K-shell 邻域识别方法（KSD）、度K-shell识别方法（DKS）以及度K-shell邻域识别方法（DKSN）对关键节点进行识别，结果表明，综合考虑因素的KSD方法识别效果最好，具有一定的实际意义。

传统上使用熵[16-17]来描述整个网络结构的复杂性和统计特性。Chen 等[18]提出结构熵来度量网络的复杂性。张齐[19]提出一种基于非广延统计力学的结构熵来度量网络的复杂性。黄亚丽等[20]基于网络节点在K 步内可达的节点总数定义K-阶结构熵，用来评估网络的异构性。Wang等[21]提出一种基于K壳和节点信息熵的改进算法，用来区分上层外壳和下层外壳中节点的重要性。Zhao 等[22]基于蛋白质复合物二阶邻域信息及信息熵和亚细胞定位提出一种必需蛋白质预测新方法NⅠE；赖强等[23]采用高度数加边、高介数加边、低度数加边、低介数加边和随机加边策略对城市公交网络进行鲁棒性优化，最后得出低度数和低介数加边策略对网络鲁棒性提升的效果较好。田文等[24]引入相对熵，结合灰色关联分析法综合评价航路点重要程度，并采用基于K-means聚类方法有效划分航路节点等级，提高了评价结果的全面准确性。

迄今为止，网络熵已成为复杂网络中评估节点重要性的有力工具，不少专家学者利用该工具设计出一系列有价值的识别方法。纵观目前超网络中基于网络熵的研究成果，王福红等[25]基于上下熵公理，通过对Tsallis熵以及Daroczy 熵进行合理处理，提出了一种度量超网络复杂性的上下熵模型，为探索超网络的复杂特性提供了新的理论基础和参考；周丽娜等[26]通过研究节点及其直接和间接邻居节点的关联关系，利用节点信息熵表征节点在超网络中的重要性，为超网络重要节点识别提供了一种新的研究视角。由于该指标是一种局部性指标，仅仅考虑了一阶邻居节点的影响，而超网络中节点的影响不仅取决于节点的局部影响，还依赖于节点的全局影响，因此，本文提出一种基于节点传播熵的超网络重要节点识别方法（PE）。该方法利用节点聚集系数和邻居数目表征节点信息的局部传播影响，通过节点间最短路径和K壳分解法反映节点信息的全局传播影响，充分考虑节点自身及其邻域节点的影响，最后利用节点传播熵来表征节点在网络中的重要性。为了验证该方法的有效性和适用性，本文选用了来自不同领域的六个实证超网络，并采用六种已有的重要节点识别方法作为比较方法，在此基础上，利用单调性、鲁棒性以及SⅠR传播模型证明了该方法的可行性。

1 相关知识

1.1 超网络定义

2006 年，Estrada 等[5]首次提出基于超图的网络称为超网络（hypernetwork），其中超图理论的基本概念和性质由Berge[27]给出，设V={v1,v2,…,vn} 是一个有限集；若ei≠φ(i=1,2,…,m)，且，则称二元关系H=(V,E) 为超图，其中vi(i=1,2,…,n) 称为超图的节点，ej(j=1,2,…,m)称为超图的超边。超图的邻接矩阵A(H)是一个N×N的对称方阵，其元素aij表示与节点vi和vj都相关联的超边数量。关联矩阵B(H)是一个N×M的矩阵，如果节点vi与超边ej关联，则bij=1，否则为0。

1.2 超度

在超网络H中，节点vi的超度是衡量节点影响力的最简单指标。与节点vi相关联的超边数量越多，该节点的影响力就越大。节点vi的超度定义为：

1.3 信息熵

信息熵于1949年由Shannon等[16]提出，信息熵和热力学熵紧密相关，所以信息熵是可以在衰减的过程中被测定出来的。因此信息的价值是通过信息的传递体现出来的。熵值越大，传播得越广，流传时间越长的信息越有价值。在图熵中，信息熵反映节点的局部重要性。网络的信息熵被定义为：

其中，Ii为节点vi的重要性。

1.4 介数中心性

超网络中，介数中心性通常根据最短超路径来定义，刻画节点对于网络中沿着最短超路径传输网络流的控制力，节点的介数中心性值越大，该节点的影响力就越大。节点vi的介数中心性[7-8]定义为：

其中，gk表示节点vj和节点vk之间的最短超路径数目，gk(i)表示节点vj和节点vk之间的最短超路径中经过节点vi的数目。

1.5 接近中心性

接近中心性衡量的是节点到超网络中其他节点的最短路径之和，若某个节点到网络中其他节点的最短路径之和最小，即该节点可以在最短的时间内进行信息传播，其影响力就越大。

对于具有n个节点的超网络来讲，节点vi到超网络中其他节点的平均距离[9]可以表示为：

di越小，节点vi与超网络中其他节点越接近。节点vi的接近中心性[8]定义为di的倒数，计算如下：

其中，dij表示节点vi到节点vj的最短距离。

1.6 子图中心性

子图中心性[5]从全局视野刻画了网络中各节点的相对重要性，反映了节点在不同子图中的参与情况。超网络中节点vi的子图中心性定义为超网络H中起止于该节点的不同长度的闭合路径之和，可用邻接矩阵特征值和特征向量表示：

其中，λj是超网络H的邻接矩阵A的特征值，uj是λj所对应的特征向量，uij表示特征向量的第i个元素。

1.7 超网络的K壳分解法

K壳（K-shell）分解法[10]作为一种从网络整体结构确定超网络中节点位置的全局性指标，其基本思想是通过迭代的方式将超网络划分为从核心到边缘的不同层次，越靠近核心的节点越具有影响力。具体划分过程为：首先，删除超网络中超度为1 的节点及超边超度为1 的超边；其次，删除后的网络中将出现新的超度为1的节点，继续删除新出现的超度为1 的节点及超边；最后，重复上述操作直至超网络中不再出现超度为1 的节点及超边超度为1的超边为止。此时所有被删除的节点Ks值为1。以此类推，直至超网络中所有节点都被赋予Ks值。如图1为超网络的3-shell分解过程示例图[10]。

图1 超网络的3-shell分解过程图Fig.1 3-shell decomposition process diagram of hypernetwork

1.8 核度中心度

核度中心度kd s指标由周丽娜等[10]人提出，该指标有效改善了超网络K-shell分解方法的区分度。它综合考虑节点超度和K-shell 两种指标的性质，利用欧氏距离公式定性计算超网络中节点的核度值，节点vi的核度中心度定义为：

其中，dH(i)表示节点vi的超度，Ks(i)表示节点vi的Ks值。

2 构建节点传播熵度量指标

当节点在整个超网络中有效地传播信息时，该节点的重要性及其对其他节点的影响力就会增强。由于节点在网络中的传播能力受节点局部拓扑信息和全局拓扑信息的影响，在评估超网络中节点的传播能力时，本文从熵的角度出发综合考虑节点的聚集系数、邻居数目、K 壳分解法以及最短路径，充分考虑节点自身及其邻域节点的影响，提出一种节点传播熵指标来度量节点在网络中的重要性。

2.1 节点的局部传播能力

网络是由若干“群”或“团”构成，每个群内部的节点之间连接相对紧密。在超网络中，通常用聚集系数来衡量节点的聚类程度。随机游走理论中，信息是从网络中的某个节点以一定的概率传播到与其连接的其他节点，因此，节点的聚集系数越大，信息越容易被传回始发点，节点的传播能力也就越差。进一步，本文考虑聚类系数对节点局部传播能力的影响。节点的聚集系数定义为：

其中，Mi表示节点vi的kH(i)个邻居节点间实际存在的超边数，kH(i)(kH(i)-1)表示kH(i)个邻居节点间最大可能存在的超边数。

由于节点的聚集系数度量与朋友的朋友成为朋友的概率，这就表明节点的局部传播能力不仅与一阶邻居的数量有关，还与二阶邻居的数量有关。因此，本文综合考虑节点的聚集系数及其邻域数量，用来描述节点的局部传播能力，定义如下：

其中，N1(i)和N2(i)分别表示节点vi的一阶和二阶邻居节点数量，CH(i)表示节点vi的聚集系数。

2.2 节点的全局传播能力

超网络中节点的传播能力不仅取决于节点的局部拓扑信息，还依赖于节点的全局拓扑信息。K壳分解法作为描述节点在网络中所处位置的全局指标，可以用来描述每个节点与整个网络之间的关系以及不同节点之间的关系。当节点的邻域节点的Ks值较大时，节点的传播能力就会增强，但如果节点间的距离较大，就会减弱节点的传播能力。因此，在评估节点的传播能力时还需要考虑节点间最短路径的影响。

综合考虑节点所处位置以及最短路径对节点传播能力的影响，将节点的全局传播能力定义为：

其中，Ksi表示节点vi的Ks值，Dij表示节点vi到节点vj之间的最短路径。

2.3 节点传播熵

在图熵中，信息熵可以反映节点的重要性，而节点的重要性需要考虑节点的所有邻接节点，由于邻居节点的贡献不同，本文在兼顾节点局部和全局拓扑信息的同时，充分考虑节点自身及其邻居节点的影响，基于信息熵对节点传播熵进行以下定义：

其中，N(i)表示节点vi的邻居节点集，-IjlnIj表示邻居节点的贡献，Ii为节点vi的相对重要度函数，计算如下：

3 基于节点传播熵的重要节点识别算法

基于节点传播熵的重要节点识别方法构造的基本思想是从熵的角度综合考虑节点的聚集系数、邻居数目、K 壳分解法和最短路径对节点传播能力的影响，进而评估网络中节点的重要性。由于聚集系数和邻域数目能体现节点的局部拓扑信息，而K壳分解法和最短路径表征了节点的全局拓扑信息，兼顾这两种拓扑信息，利用信息熵度量网络结构复杂性，并对每个节点自身及其邻域节点进行综合考察，从而给出一种基于节点传播熵的识别超网络中重要节点方法，简称为PE算法，其主要算法描述如下所示。

算法1PE算法

输入：超网络H=(V,E)

输出：超网络中各节点传播熵PE值

1.fori=1 ton

2.根据公式（8）、（9）计算节点的局部传播能力;

3.根据公式（10）计算节点的全局传播能力;

4.根据公式（11）计算节点的相对重要度函数;

5.forjinN1(i)

6.根据公式（12）计算节点的传播熵值;

7.end

8.end

由以上描述可知，PE 算法要遍历网络中的每个节点，在计算节点的局部传播能力时，考虑节点及其二阶邻域拓扑结构间的关系，故时间复杂度为O(n2)；在计算节点的全局传播能力时，节点的K壳重要性指标的时间复杂度为O(n)，节点到其他节点间的最短路径的计算中使用了Dijkstra 算法，时间复杂度为O(n2)；在计算节点的PEi值时，时间复杂度为O(n)。因此，本文提出的PE算法的时间复杂度为O(n2)。其中，n为超网络中节点的总数。

4 实验结果与分析

4.1 有效性分析

为了验证本文提出的PE 方法的有效性和准确性，首先以蛋白复合物超网络[28]为例进行仿真分析。该网络包含2 314个人类蛋白质节点以及蛋白质之间相互作用形成的1 342 条复合物超边，根据在线基因必需数据库（online gene essentiality（OGEE），https：//v3.ogee.info/browse）[29]查询蛋白质的重要性。使用精确率指标评估七种不同中心性指标识别的蛋白复合物超网络中的必需蛋白质。该指标仅考虑前k个节点是否准确预测，其值等于前k个节点中准确预测的节点比例。精确率定义如下：

其中，np表示前k个节点中包含的重要节点数。在该蛋白复合物超网络中，k设置为1 000。从表1 可以看出，相比较其他重要节点识别方法而言，PE方法的精确度最高，表明PE 方法可以准确识别出超网络中的重要节点。

表1 七种不同中心性方法识别重要蛋白的精确率Table 1 Precision of seven different centrality methods for identifying essential proteins

4.2 实验数据

在实验中采用了六种来自不同领域的实证超网络，分别为：Karate超网络、西宁市公交超网络、都柏林感染超网络、Facebook 电视节目超网络、药物靶标超网络以及科研合作超网络。各超网络的统计特征如表2 所示。其中n为超网络中节点总数，m为超边总数，为平均超度，为平均最短路径长度，CH为超网络聚集系数。

表2 超网络的统计特性Table 2 Statistical characteristics of hypernetworks

4.3 评价标准

4.3.1 单调性评价指标

本文采用单调性评价指标M(R)来量化不同重要性评估方法的分辨率，定义如下：

其中，R为重要节点识别方法得到的每个节点的重要性排序向量，n为网络节点数目，nr表示重要性相同的节点数量。M(R)的取值介于[0，1]。如果M(R)=1 则排序向量R是完全单调的，说明该识别方法能将网络中所有节点的重要性完全区分；反之，则表示网络中所有节点的重要性相同。M值越高，表明识别方法的区分能力越高。

4.3.2 鲁棒性评价指标

本文从鲁棒性的角度通过移除节点后对网络连通度的影响来评估重要节点识别方法的准确性。超网络中，连通分量是一个网络子超图，其中子超图中的任意两个节点是连通的。最大连通子图是指随着节点移除网络分解出的多个连通子超图中包含节点数最多的连通分量，可以反映超网络的连通性。如果移除的是重要节点，最大连通子图的规模会变小。网络的最大连通系数定义为移除节点后网络最大连通子图中包含的节点数与原始网络总节点数之比，计算方法如下：

其中，nc表示移除部分节点后网络的最大连通子图包含的节点数，n为原始网络总节点数。

利用最大连通系数来计算网络的鲁棒性，计算公式如下：

其中，rj表示移除j个节点后的最大连通系数。R越小，网络崩溃得越快，说明移除的节点越重要。

4.3.3 SIR传播模型

本文采用SⅠR（susceptible-infected-removed）模型来检测超网络中重要节点的传播能力，SⅠR模型将网络中节点的状态划分为三类：易感状态S、感染状态I以及恢复状态R。SⅠR模型传播过程如图2所示。

图2 SⅠR传播模型图Fig.2 Diagram of SⅠR propagation model

在传播初始阶段，网络中一个或多个节点处于感染状态，其余节点均处于易感状态。在每个时间步中，处于I状态的节点以传播概率β感染处于S状态的邻居节点，同时以概率γ进入恢复状态，且不再被感染。重复上述传播过程直到网络中没有处于感染状态的节点。在整个SⅠR传播过程结束后，将网络中处于R状态的节点数量视为节点的传播能力，记作F(t)。

4.4 实验分析

4.4.1 单调性实验分析

为了度量PE 方法对重要节点的区分度，本文选用超度(dH)、介数中心性（BC）、接近中心性（CC）、子图中心性（SC）、K 壳分解法(Ks)、核度中心度(kd s)共6 种识别方法作为对比方法，利用单调性指标评估6种对比方法与本文所提出的PE方法的分辨率。表3记录了不同识别方法在6 个真实网络中的单调性值；图3 则更为直观地呈现了不同方法之间的差异。

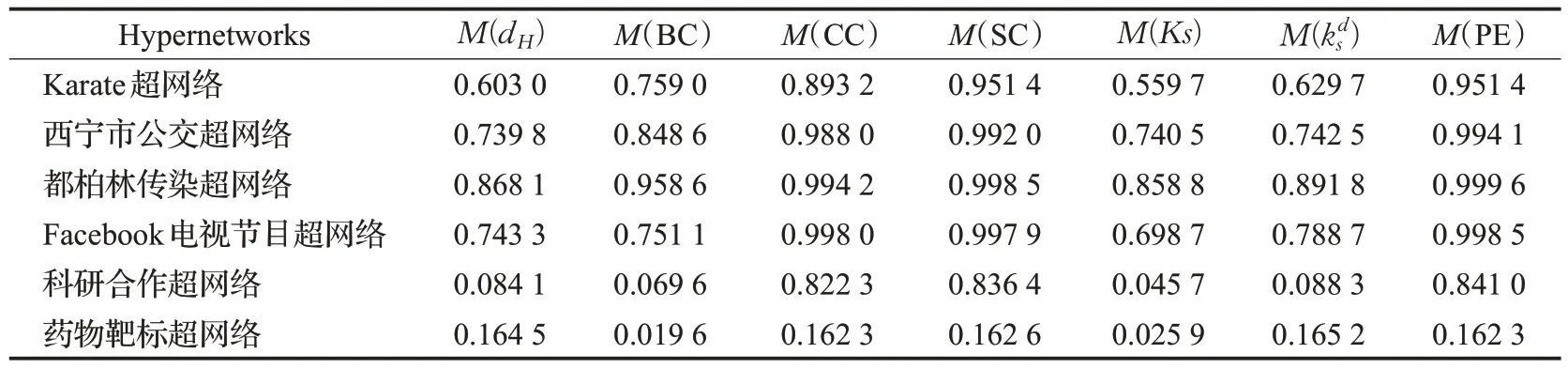
表3 不同识别方法的单调性指标MTable 3 Monotonicity index M of different evaluation methods

图3 不同评估方法的单调性指标MFig.3 Monotonicity index M of different evaluation methods

结果表明，PE 方法在5 个真实超网络中表现较好。此外，CC和SC方法的区分度也很好。与其他6种方法相比，PE方法在大多数情况下的M值最高且接近1。因此，PE方法能够较好地区分节点的重要性。

4.4.2 鲁棒性实验分析

为了进一步分析PE 方法识别的节点的重要性，本组实验分别通过超度(dH)、介数中心性（BC）、接近中心性（CC）、子图中心性（SC）、K 壳分解法（Ks）、核度中心度(kd s)和节点传播熵（PE）7种方法将6种实证超网络的所有节点进行重要性排序，并按照重要性排序依次移除一定比例的节点，基于连通性分析删后网络的最大连通系数，以此来评估7 种不同重要性度量指标的鲁棒性。移除节点后网络的最大连通系数变化曲线图如图4 所示；不同重要性度量指标的鲁棒性值如表4所示；图5则更为直观地呈现了不同方法之间的鲁棒性差异。

表4 不同识别方法的鲁棒性值RTable 4 Robustness values R of different evaluation methods

图4 超网络最大连通系数Fig.4 Maximum connectivity coefficient of hypernetworks

图5 不同评估方法的鲁棒性值RFig.5 Robustness value R of different evaluation methods

从图4 可知，在Karate 超网络中，当移除节点的比例到0.3的时候，通过PE方法移除节点后的最大连通系数变化比较明显，较初始阶段下降85%，说明相较于其他几种方法，PE 方法具有一定的优势。在其余超网络中，表现最优的是BC方法，这是因为BC方法可以准确识别网络中的“桥”节点，随着高介数节点的移除，则会断开网络的连通性，因而网络的最大连通系数变化比较明显。Ks以及kd s方法在移除节点初期，最大连通系数变化明显的原因是，二者均是在dH的基础上提出的改进方法，按此方法选择的重要节点移除时，节点的邻居数量相对其他方法更多，移除节点及其连边后最大连通子图的规模会锐减。在科研合作超网络和药物靶标超网络的实验中，移除节点初期阶段，PE方法的效果不如BC、dH、Ks以及kd s方法，但是后期的效果是具有优势的，可见，对于网络的蓄意攻击，PE 方法考虑了长期的收益。此外，在整个鲁棒性实验中，PE方法的效果明显优于CC和SC方法。

由表4 可知，鲁棒性R值越小，该方法的性能表现越好。图5 可以更直观看出，在5 个真实超网络中，PE方法要优于CC 和SC 方法，与其他方法相比不明显，但是与超度相比，PE方法提高了节点重要性的区分度，与BC、CC 方法相比，PE 方法在时间复杂度上得到了有效提升。随着网络规模的扩大，PE 方法的鲁棒性也在提升，在对科研合作、药物靶标超网络进行攻击时，由于其平均路径长度相对较大且聚集系数较低，PE 方法的效果相对明显。虽然PE方法不是降低超网络连通性的最佳选择，但该方法计算复杂度相对较低且倾向于优先破坏网络中的传播核心结构。

4.4.3 SIR传播模型实验分析

为了验证PE方法识别的重要节点在超网络中的传播能力，本节通过在6 个真实超网络上使用SⅠR 模型模拟传播过程，对比不同方法到达稳态时的感染节点数来考察节点的重要性。本实验选取7 种算法识别的重要节点排序列表中前10 个节点作为初始感染节点，观察每一时间步网络中感染过的节点数目以及最终到达稳态时感染过的节点数目，为保证传播过程正常进行，设定传播概率为网络的传播阈值，即，其中为网络平均超度，恢复率γ=0.1。实验结果如图6所示。

图6 节点传播能力Fig.6 Node propagation ability

在SⅠR 模型的实验中，传播感染的节点数越多，证明所识别的节点在网络中的重要性越高。通过对比图6 中6 个真实网络的传播情况可知，对于各个传播时间通过PE方法识别的重要节点的传播能力明显优于其他六种方法，其传播曲线始终位于各方法曲线之上，表明该方法识别的重要节点最终到达稳态时感染过的节点数目是最高的。在科研合作超网络中，PE 方法的传播效果完全优于其他方法，原因是该网络聚集系数相对较小且网络节点连接稀疏，对该类型网络进行信息传播时，PE 方法的优势较明显。从图6 的曲线斜率来看，传播到达稳态之前通过PE算法识别的节点传播能力的曲线斜率要高于其他6 种方法，表明通过PE 算法识别的节点在网络中的传播速度较快，传播范围较广，进而验证了本文所提出的方法可以有效识别超网络中的重要节点。

5 结语

本文从熵的角度综合考虑节点自身聚集特性、所处网络位置及其路径信息对节点传播能力的影响，提出了一种基于节点传播熵的超网络重要节点识别方法PE。通过对6 个真实网络进行仿真验证，结果表明PE 方法具有高区分度，明显的传播优势，可以在不同类型的超网络中发现具有强传播能力的节点。此外，PE 方法的时间复杂度为O(n2)，适用于大规模超网络。

由于真实网络呈现出动态性以及多层多级多维的特征，本文提出的方法还存在一定的不足，在未来的工作中会结合网络的时空特性，将提出的PE 方法应用于多层超网络的重要节点识别研究。