改进Informed-RRT＊的移动机器人路径规划算法研究

靳午煊，马向华，赵金良

1.上海应用技术大学 电气与电子工程学院，上海 201418

2.上海电气电力电子有限公司，上海 201916

现如今移动机器人已广泛应用于交通导航、特种作业、医疗餐饮服务等行业中[1]。路径规划作为移动机器人的核心技术，一直是学者们研究的热门话题。移动机器人全局路径规划的目的是能够在已知环境中快速高效地找到一条最短路径。对于传统路径规划算法，有基于搜索的Dijkstra[2]和A*[3]算法也有遗传算法[4]和模拟退火法[5]等智能优化算法，但传统的全局路径规划算法规划效率过低且不适合如今复杂多变的环境。1998年，提出了基于采样的快速搜索树（rapidly-exploring random tree，RRT）[6]由于其随机性强，规划效率快的特点得到了广泛关注。由于RRT算法规划出的路径并不是最优的，2010年，提出了RRT*[7]算法，在原RRT算法基础上加入重选父节点进行重布线的策略，使其拥有了渐进最优性。2014 年，在RRT*的基础上加入椭圆状态子集的概念提出了Ⅰnformed-RRT*[8]算法，加快了算法的收敛速度。为了追求路径搜索和规划的效率，近年来国内外对Ⅰnformed-RRT*算法的改进也有很多。其中比较突出的改进是将Ⅰnformed-RRT*算法与一些较完备的避障或者规划算法相融合。文献[9]将动态窗口法融入Ⅰnformed-RRT*，使其更好地适用于移动机器人并证明了此方法对所有RRT 类算法的适用性。文献[10]将Ⅰnformed-RRT*与人工势场法融合，加入自适应步长方法在静态和动态障碍物的适应性。文献[11]采用融合有向D*的策略，使规划出的路径在转弯处得到优化，且更适合连续小洞和狭窄通道。此类融合算法在提升规划效率的同时将耗费过多内存，需要更高性能的移动机器人才能满足规划需求。还有一些学者对Ⅰnformed-RRT*算法本身进行改进。其中文献[12]采用混合抽样方法代替随机抽样，使移动机器人在复杂环境中的规划效果得到了提高。但对于较简单的环境算法效果提升并不明显。文献[13]将参考路径划分为一定数量的路径段并逐个优化这些段来解决在多曲线路径中的收敛问题，但此方法并不适合所有现实或者仿真环境。文献[14]的引入改进的Metropolis接受准则筛选每次迭代生成的新节点使算法更短时间找到最优解但会使算法丧失一定的随机性。文献[15]采用反向扩展策略，当遇到障碍时快速更新采样区间，在障碍物的边界区域获得接近最优路径成本的可行路径，此算法保留了原算法的随机性但缺乏规划时的目的性。

针对现如今Ⅰnformed-RRT*算法研究中存在的问题，采用节点优化方法对此算法进行改进。从随机节点分布，新节点的偏置生成对路径规划环节进行优化，然后对规划出的路径采取节点减冗余策略，并在节点转折处采用对称极多项式曲线法进行平滑处理。通过与原算法的对比，验证改进算法的可行性。

1 Informed-RRT＊算法

1.1 RRT＊算法

RRT*算法在RRT算法规划好的随机树上加入了重选父节点和重布线的操作。重选父节点的原理如图1所示，以Qnew（节点J）为圆心，以定义好的半径画圆，圆内包含了原始父节点（节点F）在内的4个潜在最优父节点，分别为节点E、节点F、节点Ⅰ和节点G。由图定义好每段路径的代价，其中原始路径A-C-F-J的代价为4+6+4=14；以节点Ⅰ为潜在最有父节点的=路径A-C-F-Ⅰ-J的代价为4+6+6+4=20，比原始路径代价高，则不考虑。同理可知以G节点作为父节点的A-E-G-J代价为18；以节点E为父节点的路径A-E-J代价最低，为11，则选择节点E作为最优父节点。如图1（b）便是重选父节点后的结果。

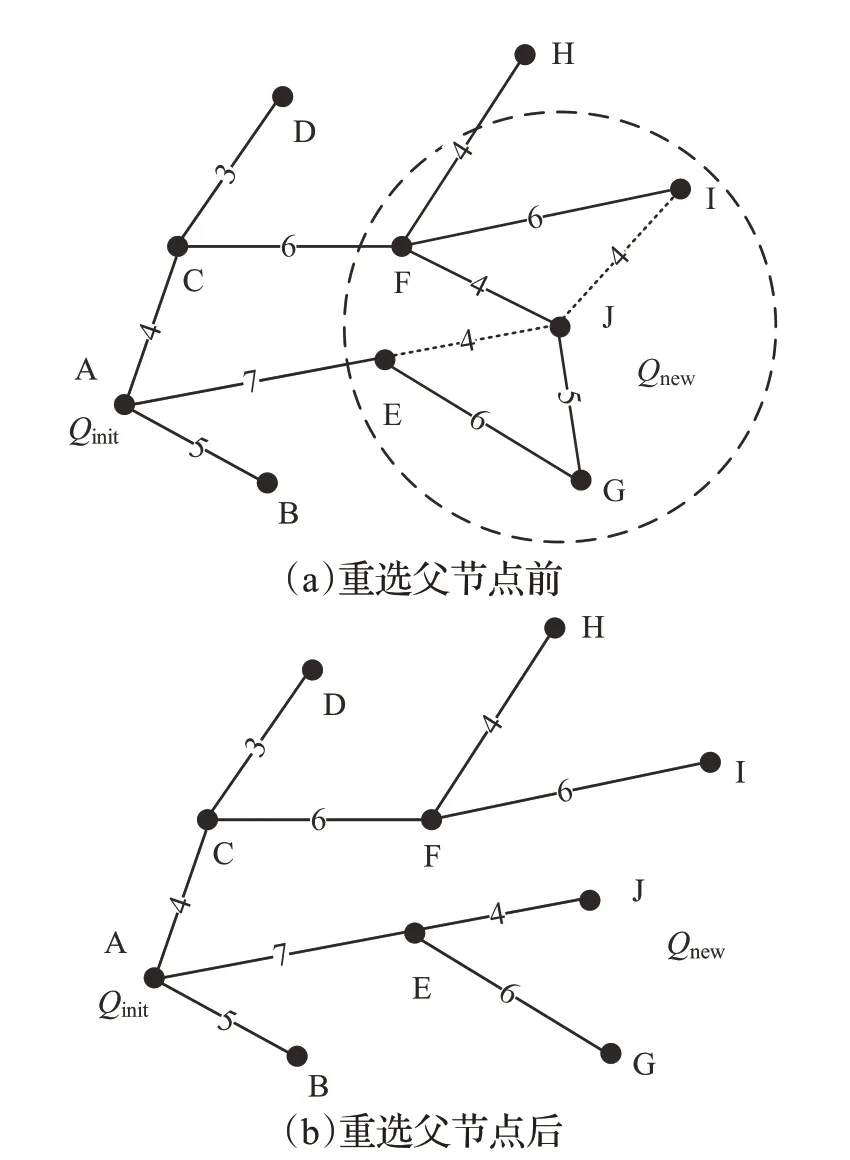
图1 重选父节点策略Fig.1 Reselecting parent node policy

RRT*算法的随机树重布线原理：为了进一步降低收敛的路径成本，为Qnew节点选择可连接的下一个临近节点。如图2 所示Qnew的临近节点为E，F，G，Ⅰ。其中到达F节点的A-E-J-F代价为7+4+4=15。而原本的路径A-C-F代价为4+6=10，所以此路径不做重新布线。对于到达Ⅰ的A-E-J-Ⅰ的代价为7+4+4=15；而原始路径AC-F-Ⅰ的代价为4+6+6=16。所以用A-E-J-Ⅰ代替A-C-F-Ⅰ进行重布线，同理可知A-E-J-G代价大于原始路径A-EG，故不做重布线。构成新的路径图2（b）所示。

1.2 Informed-RRT＊算法

Ⅰnformed-RRT*算法引入了椭圆状态子集的概念，如图3 所示，继承了RRT*算法的概率完备性和渐进最优性，通过椭圆状态子集限制采样空间，加快了收敛过程的速度。其中Cmin作为椭圆的焦距，长度为起始点到终止点的距离。Cbest为椭圆的长轴，长度为算法规划的路径长度。Ⅰnformed-RRT*算法根据Cbest和Cmin两个参数建立椭圆采样空间。Cbest随着重选父节点操作不断减小，椭圆短轴也不断减小，此时采样空间会不断缩小，收敛速度不断加快。

图3 椭圆采样区示意图Fig.3 Diagram of elliptic sampling area

Ⅰnformed-RRT*算法为在椭圆状态子集U中的随机采样，采样样本是由单位圆中的均匀分布的采样样本经过L转换矩阵变换得到。

这种变换可以由超椭球矩阵S的Cholesky分解得到。

对于椭圆，可以仅从长轴和焦距计算变换，长轴对齐的坐标系中的超椭球体矩阵是对角矩阵。分解得到的超椭球体对角矩阵为：

由上式可得：

另外从椭圆采样坐标系到圆形采样坐标系的变换可以通过Wahba问题的求解方式解决：

其中，U∈ℝn×n，V∈ℝn×n并且两者都是酉矩阵可进行奇异值分解:U∑VT=M，M矩阵可由长轴的外积和单位矩阵第一列相乘得到。

综上椭圆状态子集内由圆形采样区转换后的采样点：

2 改进Informed-RRT＊算法

2.1 自适应t-分布的采样节点优化

Ⅰnformed-RRT*算法采用与RRT*算法相同的完全随机的采样方法，目的是避开障碍物找寻一条最短的路径。其完全随机性导致大量节点分布在非必要的空白地区，浪费了内存并且降低了采样的效率。为克服以上缺点，引入t-分布的概率密度函数对随机树的采样环节进行优化，具体要求是在距离障碍物较远的地方降低随机采样节点Qf的分布概率，在距离障碍物较近的地方增加随机采样节点Qf的分布概率，对于更为复杂的障碍物环境自适应地进行调整。这样在避免浪费节点的同时增加节点重选过程中障碍物附近的节点数量，以获取更为精致的路径。

t-分布又称为Student分布，其概率密度表达式为：

式中，n为t-分布的自由度，当自由度n较小时，概率密度函数较为温和，中间极值较低，两端值较高，当n较大时，概率密度函数较为陡峭，中间极值较高，两端值较低，不同自由度的t-分布的概率密度函数如图4所示。

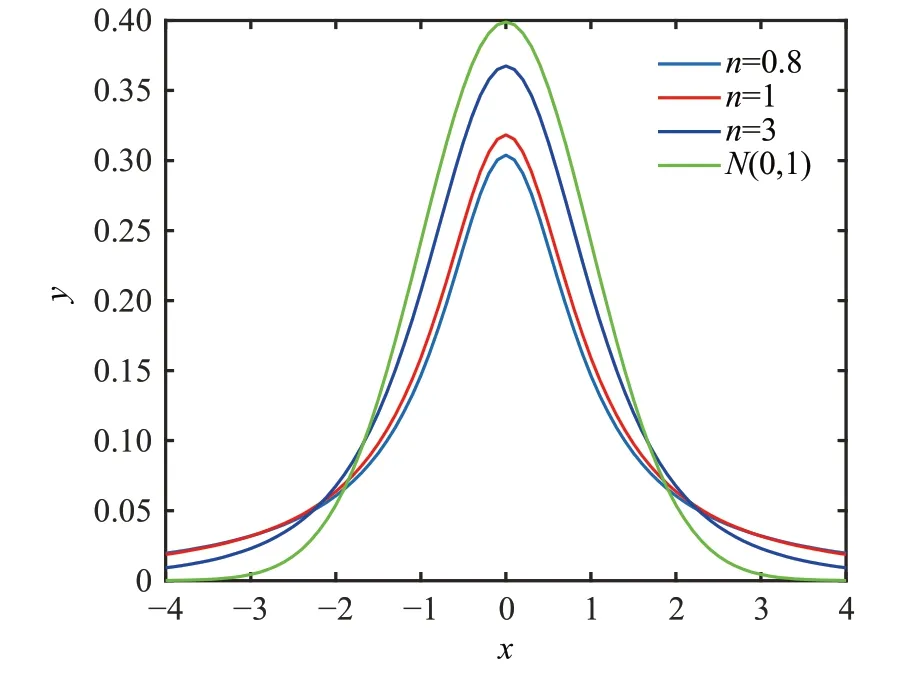
图4 t-分布概率密度函数Fig.4 t-distribution probability density function

设定L为采样节点Qf到障碍物的距离，L>0 。可以看出采样节点距离障碍物越远，L越大，采样概率越低，反之采样概率越大。故t-分布优化的采样概率分布函数为：

采样概率分布函数如图5 所示，当n较大，如n为∞时，t-分布为高斯分布，采样概率分布函数较为陡峭，在距离障碍物较近时，分布函数值较小，对采样点的增加量较小，适合较为简单的障碍物环境。对于更加复杂的障碍物形状，自适应地降低自由度n的大小，如n=1时，t-分布为柯西分布，在距离障碍物越近的情况下，采样点的分布概率增加量有所提高。引入t-分布对采样环节进行优化，自适应地调整t-分布自由度的大小，可以避免单一分布函数对不同环境下的同一处理，降低规划效率。

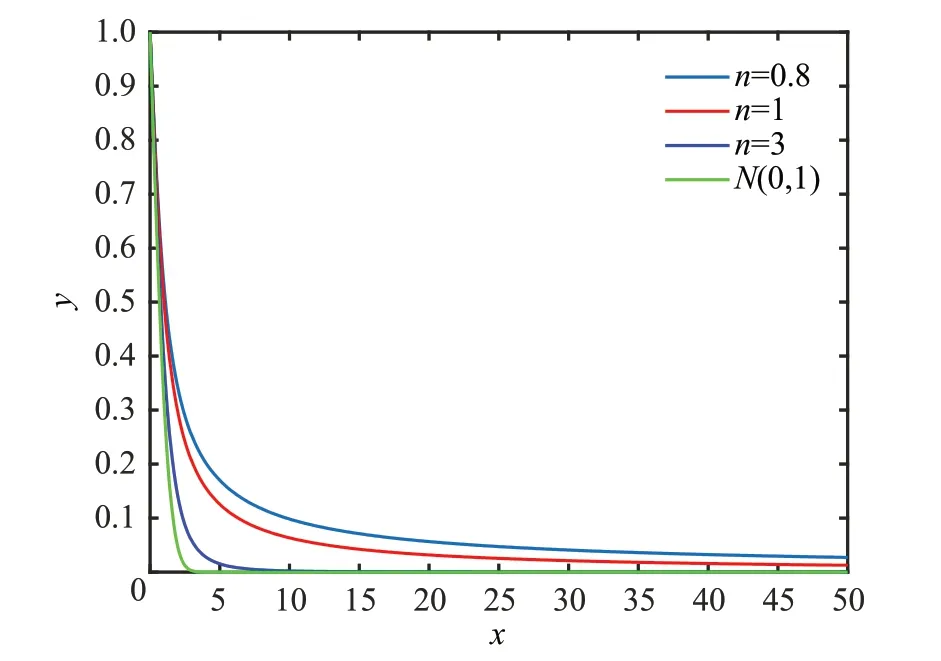
图5 采样概率分布函数Fig.5 Sample probability distribution function

对采样环节的优化，使更多的采样点分布在障碍物周围，首先算法会根据基础的快速搜索树算法规划出一条初始路径。在t-分布优化下，初始路径会贴近障碍物。在节点重选环节，有更多的备选节点分布在障碍物附近，而在空白区域备选节点分布较少，将会在提高算法精度的同时降低节点浪费从而提高算法的规划速率。

2.2 椭圆焦距节点偏置策略

Ⅰnformed-RRT*算法的随机树的生长过程是完全随机的，在近几年的研究中，有学者采用以目标点Qgoal为偏置点的方法使随机树的生长具备了目的性，但这一策略会产生一定的弊端，较大的单一偏置量会让整体算法丧失随机性，从而有陷入局部最优的可能。

为了避免这一问题，已知椭圆状态子集中焦距Cmin为理想的最优路径，故将偏置扩展为整个椭圆焦距，以椭圆焦距作为偏置点的集合，椭圆的焦距Cmin是初始节点Qinit到目标节点Qgoal的直线距离，每个采样随机点概率的选取椭圆焦距上的偏置点作为新生长节点的偏置，直到以Qgoal为偏置点结束。采用椭圆焦距偏置，使随机树的生长贴近于最优路径，在避免局部最优的同时增加了算法随机树生长的目的性，加快椭圆采样空间收敛速度。

以节点作为原点，以椭圆焦距方向作为x轴，节点Qgoal方向作为x轴的正方向，垂直于焦距的方向作为y轴建立直角坐标系，如图6所示。在椭圆焦距上等距取m个点作为新节点Qnew生长的可选偏置点，分别记为x1,x2,…,xm-1,xm，其中xm为节点Qgoal。当随机采样节点Qf的x坐标位于xn-1点到xn点之间时，只考虑xn-1之后的点，选取xn,xn+1,xn+2,…,xm-1,xm作为偏置点。随机采样节点Qf1和Qf2在椭圆焦距上的可选偏置点如图6所示。

图6 焦距偏置点分布图Fig.6 Distribution diagram of bias points at focal length

为了在规划时避免陷入局部最优，应保留随机树无偏置随机生长的本领，故以K为偏置概率系数，以ρ1和ρ2作为向随机采样点Qf和偏置点前进的步长。若Qf的x坐标位于xn-1点到xn点之间，此时新节点Qnew以xn+1为偏置点生长的概率为：

其中，概率服从以均值为μ=xn，方差为σ的高斯分布函数。

此时新节点Qnew扩展点可表示为：

两个方向产生的步长组成的平行四边形如图7 所示，对角线的方向便为新节点Qnew的方向，Qnewp为原始无偏置的新节点。

图7 焦距偏置随机树生长图Fig.7 Growth diagram of focal length bias random tree

2.3 重选祖辈节点策略

Ⅰnformed-RRT*的随机树生长环节中会产生较多的节点，过多的节点会在节点重选环节使规划出的路径产生较多的转折，并不适合实际机器人的运行。在节点重选的过程中，每一代节点本身都记录着顺序（辈分）和代价，这给重选祖辈节点提供了支撑。相比于计算节点到Cmin的距离进行比较重连接的Dougla-Peucker减冗余算法，采用重选祖辈节点的方法直接调用算法中已知的节点信息，路径弯折概率较小且效率更高。

在算法规划出最优路径后从节点Qgoal开始再次向节点Qinit进行选择重新布线，操作如下：

（1）对从Qgoal到Qinit的中间节点进行标号，记为Qn,Qn-1,…,2,1。由于Qn并不是Qgoal的父节点，故先只将节点Qn加入重选集Z中。

（2）已知Qn-1为Qn的父节点，则Qn-2为Qn的祖辈节点，连接Qn和Qn-2，判断连接线是否有障碍物，若有障碍物则将Qn-1加入Z中，然后以Qn-1向前重选；若连接线无障碍物，则向前连接Qn和Qn-3，再次判断是否有障碍物，依次类推，直到重选至Qinit节点停止。

（3）依次连接重选集Z内的节点，最终路径与Qgoal相连，即为减冗余后的路径。

2.4 转折节点平滑法

经过节点减冗余后的路径，不够平滑且路径角度偏转过大，不适合实际移动机器人运行。需要采取适当的路径平滑策略。作为经典的路径平滑方法，圆弧-直线法在平滑后生成的路径曲线的曲率和移动机器人运行时的向心加速度会发生跳变，影响机器人的精度和效率。而对于对称极多项式曲线，其与直线连接时曲率连续，且曲率有界，路径满足几何学特征，并能满足机器人运行的动力学要求。

对称极多项式曲线在路径转折点的平滑原理如图8所示，此时生成路径P0→P1→P2，路径P0→P1为对称极多项式曲线，路径P1→P2为直线。

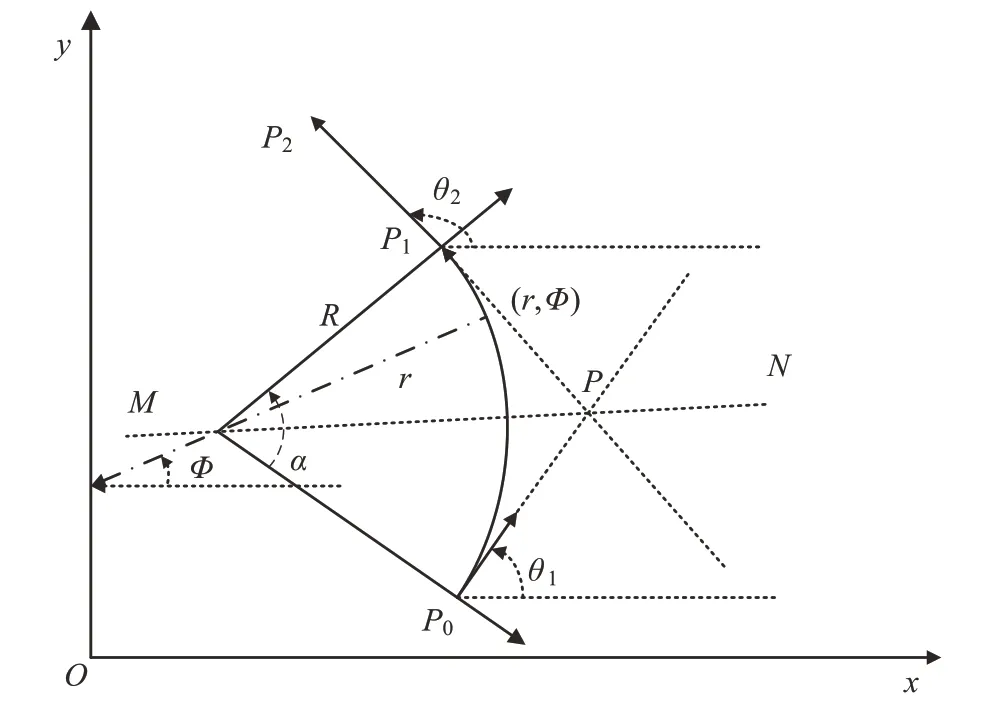
图8 对称极多项式曲线平滑路径Fig.8 Smoothing path of symmetric polar polynomial curves

P0是P1关于MN的对称点。x-y是直角坐标系r-φ为极坐标系，确定对称极多项式曲线方程为：

求解平滑路径的过程就是确定系数R和α的过程，α=θ2-θ1，P点的坐标为：

初始曲率半径：

由于移动机器人具有一定的动力学特征，在转弯时，为了避免机器人与地面打滑的现象，必须要有一定的向心力。这样当机器人以一定速度v行驶时，就会存在一个最小的拐弯半径Rmin，此时路径的曲率半径应大于移动机器人运行时的最小转弯半径，也就是生成路径的最大曲率需满足：

机器人实际运行过程中，会有多段直线连接的情况，需在平滑路径时添加若干个过度状态Ptrans，用多段直线和多条对称极多项式曲线来连接初始点和目标点。其中初始位姿与目标位姿相交平行和转交大于的多段对称极多项式曲线连接，如图9所示。

图9 多段对称极多项式平滑路径生成Fig.9 Multi-symmetrical polar polynomial for smooth path generation

3 仿真实验与分析

3.1 平面空间仿真

采用PyCharm2019 环境，设置障碍物环境大小为300×300。起始点坐标为（10，10），由图中绿色点表示；目标点坐标为（250，250），用红色点表示。规划出的路径由深蓝色线或粉色线表示障碍物用黑色块状物表示。

如图10 和图11 分别为简单障碍物和复杂障碍物环境下原算法和改进算法对比实验。其中图10（b）和图11（b）中连接起始点和目标点的红色虚线为改进算法中椭圆焦距。

图10 简单障碍物环境下仿真对比Fig.10 Simulation comparison in simple obstacle environment

图11 复杂障碍物环境下仿真对比Fig.11 Simulation comparison in complex obstacle environment

Ⅰnformed-RRT*算法和改进Ⅰnformed-RRT*算法在简单障碍物环境下仿真的对比结果如表1所示，节点数目减少了4.18%，表明保证在规划时改进算法在提高节点利用率的同时能有效地节省使用的内存。在搜索时间和路径长度上分别减少了22.84%和10.98%，可以看出在简单障碍物环境下改进后的算法效率更高，规划出的路径更优。

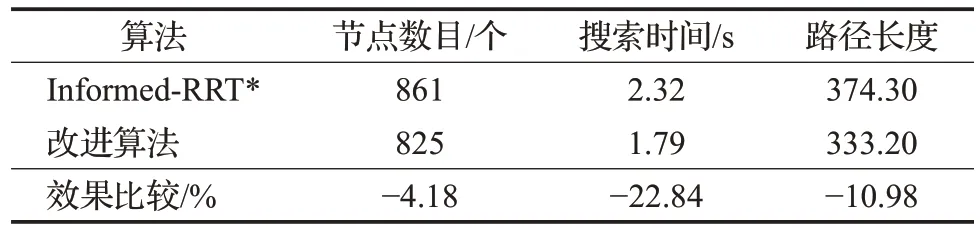
表1 简单障碍物环境30次仿真平均值Table 1 Average values of 30 simulations of simple obstacle environment

复杂障碍物环境下Ⅰnformed-RRT*算法和本文改进Ⅰnformed-RRT*算法仿真对比结果如表2所示，在复杂障碍物环境下改进算法比原算法节点数目少了17.12%，在节点利用率上有了明显的提升，并且搜索时间上减少了25.65%，路径长度上缩短了8.50%。可以看出改进算法对复杂障碍物环境也有着较强的适应性。

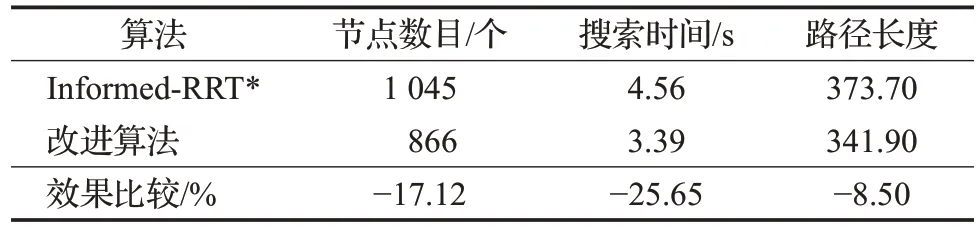
表2 复杂障碍物环境30次仿真平均值Table 2 Average values of 30 simulations of complex obstacle environment

路径平滑环节首先采用重选祖辈节点的方式对整条路径上的节点减冗余，减少路径的转折。复杂障碍物环境下减冗余后的结果如图12所示。其路径节点数量由图11（b）的86 减少为10。然后对减冗余后的路径采用对称极多项式曲线法进行转折处的平滑，最终平滑后的效果如图13所示。采用以上两种方法处理出的路径满足机器人运动时的动力学要求，且可以提高运行时的稳度和精度。

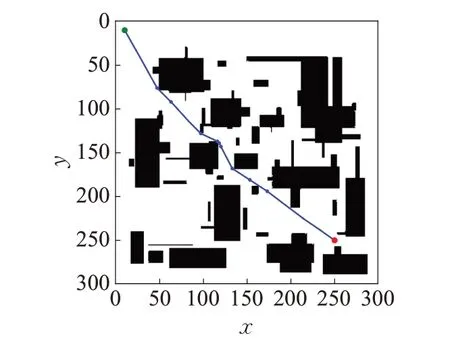
图12 路径节点减冗余Fig.12 Reducing redundancy of path nodes

图13 路径转折处平滑Fig.13 Smoothing of path bends

3.2 ROS平台实验

将路径规划优化和路径平滑在机器人操作系统（robot operating system，ROS）下的Rviz 可视化工具下进行仿真实验。首先在Gazebo 中建立机器人仿真环境，使用turtlebot3模型作为仿真机器人，如图14所示。

图14 Gazebo仿真环境搭建Fig.14 Gazebo simulation environment construction

在Rviz可视化工具下，首先采用Gmapping的SLAM方法建立地图。设置起始点坐标为（24，15，0），目标点坐标为（255，225，0），障碍物和边界用黑色表示，规划出的路径用绿色实线表示，彩色不规则线段表示邻近障碍物或边界的代价地图。如图15（a）表示采用Ⅰnformed-RRT*算法作为全局规划器规划出的路径，图15（b）为采用改进Ⅰnformed-RRT*算法作为全局规划器规划的路径。改进算法在搜索环节时更加快速，路径偏向起始点和目标点的连线，且较平滑，更加适合实际机器人运行。

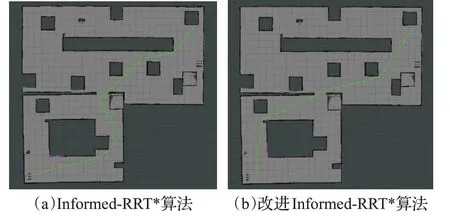
图15 Rviz环境下两种全局规划器对比Fig.15 Comparison of two global planners in Rviz environment

4 结束语

改进Ⅰnformed-RRT*算法，采用t-分布对随机采样点的分布概率进行优化，然后采用椭圆焦距偏置策略对新节点的生成进行偏置引导，在路径平滑环节采用节点减冗余策略，并在转折节点上采用对称极多项式曲线进行平滑处理。通过平面空间和Gazebo环境下的实验仿真可以看出，改进算法比原算法规划出路径速度更快，规划出的路径更优，且能在更复杂的障碍物环境中满足机器人的动力学需求。