改进孪生网络在小样本轴承故障诊断中的应用

赵晓平，彭 澎，张永宏，张中洋

1.南京信息工程大学 计算机与软件学院，南京 210044

2.南京信息工程大学 数字取证教育部工程研究中心，南京 210044

3.南京信息工程大学 自动化学院，南京 210044

滚动轴承是旋转机械设备中的关键零部件，被广泛应用于航空航天、轨道交通和工业生产等领域，一旦发生故障将直接影响整个设备的正常运行，轻则给企业造成经济损失，重则引发事故，威胁生命安全。因此，准确识别滚动轴承的故障状态对于监测机械设备健康，及时排除安全隐患至关重要。

故障特征提取是智能故障诊断的关键环节，许多研究采用先进的信号处理方法来进行故障特征提取。莫代一等[1]将基于信号共振稀疏分解方法应用到滚动轴承故障诊断中；Lei等[2]提出自适应双稳态随机共振方法来诊断行星齿轮箱早期故障；谯自健等[3]提出非对称势诱导随机共振的机械重复瞬态特征增强方法，准确增强与提取出隐含在机械监测信号中的微弱重复瞬态特征。近年来，大量学者将支持向量机（support vector machine，SVM）[4-5]、长短时记忆网络（long short-term memory，LSTM）[6-7]和卷积神经网络（convolutional neural network，CNN）[8-9]等神经网络方法应用于滚动轴承的状态监测[10]，并取得了较好的诊断效果，然而这类方法过于依赖大量的训练数据。在生产实践中，由于各种客观因素的限制，有时无法采集到充足的轴承故障信号。导致常用的深度学习模型难以得到充分训练，从而引起诊断准确率低和泛化性差等问题。因此，研究一种小样本条件下的滚动轴承故障诊断方法，不仅可以在有限的训练数据下实现对设备健康状态的准确识别，对于缓解实际工业中轴承故障信号采集困难，降低人力、物力的投入也具有重大意义。

小样本学习[11]理论近年来引起了广泛的研究，针对故障诊断领域的小样本识别问题，研究者们主要从数据增强、迁移学习和度量学习等方面进行研究[12]。吕枫等[13]提出一种基于深度嵌入关系空间下齿轮箱标记样本扩充的半监督故障诊断方法，通过对有标记样本集进行扩充来提高关系网络的泛化能力，在4%标记样本条件下，能够实现98.59%的分类准确率。Hu 等[14]使用阶次跟踪和重采样方法处理不同转速的轴承数据，在6种跨工况情况下的平均准确率远好于传统的SVM 方法。此外，张西宁等[15]、张根保等[16]、Li 等[17]均采用迁移学习方法，将模型在源域上学习到的知识迁移至目标域，使得在仅有少量目标数据的情况下也能取得很高的诊断准确率。度量学习方面，朱瑞金等[18]提出一种小样本条件下基于卷积孪生网络的变压器故障诊断方法，故障分类准确率可以达到83.2%。余浩帅等[19]设计了一种混合自注意力模块并与原型网络相结合来解决小样本情况下的故障诊断问题，所提方法在20个和100个训练样本下分别能达到83.15%和92.88%的准确率。上述方法虽然在一定程度上提高了小样本下的故障诊断性能，但仍存在诸多问题。例如数据增强方法有可能会引入噪声数据，且生成模型往往难以训练；迁移学习方法需要大量的源域数据作为辅助，迁移效果依赖于目标域和源域的相近程度和迁移策略的选择；而度量学习仅通过简单的距离度量，在训练样本很少的情况下准确率较低，但由于其计算简单、便于操作，应用相对较多。

孪生网络[20]是一种基于相似性度量的小样本学习方法，其结构简单，容易训练，已经在人脸识别[21]、语音处理[22]和签名验证[23]等领域取得巨大成效。但在很多情况下，模型效果依赖特征质量的好坏和度量方式的选择，且在测试时需要将待测样本与训练样本逐个配对来计算相似度。鉴于此，本文针对小样本条件下传统深度神经网络方法诊断准确率低、易产生过拟合的问题，提出了改进的孪生神经网络（improved siamese neural network，ⅠSNN）轴承故障诊断模型。与改进前相比，本文方法优势如下：

（1）在标准孪生网络的基础上加入了分类分支，使模型在计算样本相似度的同时，也能直接对样本进行预测分类，避免了模型测试时对数据进行逐个配对计算；此外，标准孪生网络只用到了样本间的相似度标签信息，而分类分支有效利用了每个样本自身的类别标签信息，在模型训练时能起到更好的约束作用。

（2）在特征提取环节，将采集到的时域信号数据和变换后的频域数据共同输入模型，同时利用LSTM 和CNN 提取出故障信号的时间和空间特征，从而实现对有限样本的信息充分利用。

（3）用神经网络度量替换固定距离的度量方式，使模型自适应地根据学习到的特征调整度量方式；同时为了减少网络参数，缓解模型过拟合问题，在度量网络和分类网络中使用全局均值池化层。

1 理论基础

1.1 小样本诊断问题描述

小样本学习的概念最早是从计算机视觉领域兴起的[24]，按照训练样本的多少可以将小样本学习分为三类：（1）只有一个训练样本，被称为单样本学习；（2）不存在目标训练样本，被称为零样本学习；（3）有数10 个训练样本，被称为小样本学习[25]。文献[12]指出，小样本学习的样本数量通常小于20。对于一个小样本分类任务，其目标是在给定少量训练样本的条件下，如何训练一个可以有效识别待测样本的机器学习模型。

不同于计算机视觉领域中严格意义上的小样本识别问题，查阅了大量小样本故障诊断的文献后发现，研究者们对样本数量的限定从几十个到几百个不等。因此，本文重点研究了100 个样本以内的轴承故障诊断问题。假设获取到的滚动轴承故障监测数据集为，其中Ns为训练样本个数，yi∈γ为样本的类别标签，γ∈{1,2,…,k} 是标签集合，共有k个故障类别。对于待测轴承样本集合，这里的目的是设计出一个性能优秀的故障诊断模型，从而实现对待测轴承信号xj的准确预测。

1.2 孪生网络

孪生网络的主要思想是使同一类的样本在嵌入空间中彼此接近，不同类别的样本彼此远离。在进行小样本分类时，通过计算待测样本和已知标签样本之间的距离，找到最邻近类别来确定最终的分类结果。

孪生网络使用两个权值共享的子网络同时接收两个输入样本，输出结果为两个样本的相似度[26]。其结构如图1 所示，模型首先将两个样本(X1,X2)映射到低维特征空间，然后计算两个特征向量之间的欧式距离d(X1,X2)，通过距离来衡量样本之间的相似性程度。

图1 孪生网络结构Fig.1 Structure of siamese network

由图1 可知，孪生网络的输入是一对样本，输出是它们之间的相似度。当两个样本属于相同类别时，相似度趋近于1；当两个样本属于不同类别时，相似度趋近于0。孪生网络采用对比损失函数来优化模型的训练目标，如式（1）所示：

式中，X表示输入样本，Y是样本的相似度标签，Y=1代表两个样本相似，如果在特征空间的欧氏距离较大，反而说明当前模型效果不好，此时会增加损失；Y=0 代表两个样本不相似，如果两个样本在特征空间的欧氏距离反而小的话，损失值也会变大，m为设定的阈值，‖ ∙ ‖2表示特征之间的二范数，即欧式距离。

2 ISNN故障诊断模型与诊断流程

本文分析了传统孪生网络的优缺点，通过引入分类网络构建出改进的ⅠSNN 故障诊断模型，然后设计一个基于ⅠSNN的诊断流程以实现小样本条件下的滚动轴承故障诊断。

2.1 ISNN模型框架

由于本文算法是在小样本条件下进行的，因此需充分利用每个训练样本的信息，且对网络设计不宜过深。标准的孪生网络采用欧式距离作为度量函数，度量效果取决于前期的特征提取质量，在模型测试时需要进行繁琐的样本比对。为了使模型能更加灵活地进行故障分类，充分利用有限的样本信息，以孪生网络为主干模型，在此基础上加入了分类分支，并根据轴承数据的特点重新设计了特征提取和距离度量部分，从而提出的ⅠSNN轴承故障诊断模型包含特征提取网络、关系度量网络和故障分类网络三个部分，其结构如图2所示。

图2 ⅠSNN模型结构图Fig.2 Structure diagram of ⅠSNN model

2.1.1 特征提取网络

本文搭建的特征提取网络由两个结构和参数完全相同的子模块组成，其输入是一对故障样本(Xi,Xj)。为了使训练样本中包含更多的特征信息，在数据预处理时将切分后的时域信号（长度为2 000）进行快速傅里叶变换（fast Fourier transform，FFT），得到对应的频域数据，然后把二者拼接成单个样本（长度为4 000）。相比于常用的时频图输入，本文方法通过简单拼接信号，保持了信号的一维特性，每个样本中既包含了未处理的原始时域信息，也包含了变换后的频谱信息。而时频图虽然能同时反映信号的时间与频率信息，但其丢弃了信号的原本特征信息，且在变换过程中需要人为设置固定参数，自适应性不足，也会有信息损失。此外，本文将一维数据输入模型，使得在后续的卷积、池化等步骤中仅需采用一维操作，与二维卷积相比能够减小模型参数。数据处理的具体步骤如图3所示。

图3 样本处理步骤Fig.3 Sample processing steps

每个特征提取子模块中首先利用两个LSTM层（即图2中的L1、L2）提取故障样本的时间信息，然后通过卷积层C1 进一步提取空间信息，而常规的特征提取模型一般仅采用堆叠CNN 的方式进行特征提取。LSTM是循环神经网络的变体，可以缓解训练中的梯度消失现象[27]，常被应用于时序性数据的分类和预测问题，其模型结构如图4所示。

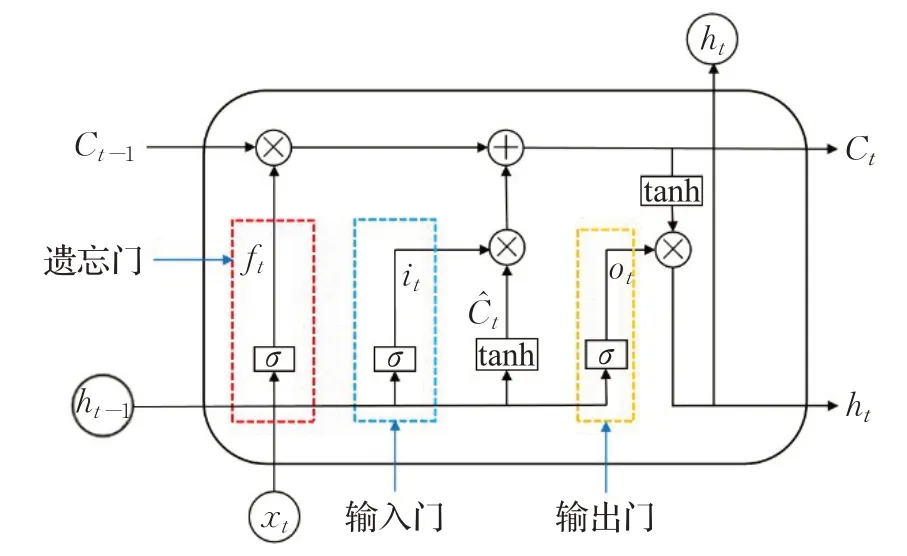
图4 LSTM结构示意图Fig.4 Structure schematic diagram of LSTM

LSTM的最小细胞单元包括遗忘门、输入门和输出门三个部分，它们决定了样本中的哪些信息应该被丢弃、存储和输出，其计算方法如式（2）~（4）所示：

式中，σ是激活函数，输出范围是0~1，ω和b表示权重和偏置，ht-1是前一个单元的输出，xt是当前输入。

本文将样本维度重塑为40×100输入LSTM，经过卷积后尺寸变为16×332。在卷积层后接入一个最大值池化层P1 对卷积结果进行下采样，将特征减小至16×110并输出到下一环节。此外，本文将训练样本以成对的方式输入ⅠSNN 模型，可以极大增加模型的训练次数。假设有n个故障样本，每次向模型输入一对样本，则一共可以进行C2n次有效训练。

2.1.2 关系度量网络

关系度量网络的作用是将输入的两个特征向量f(Xi)和f(Xj)映射为相似度概率，当两个样本相似时，输出概率为1，当两个样本不相似时，输出概率为0。常用的固定度量方式过于依赖特征提取网络学习到的特征嵌入空间质量，本文利用神经网络来度量特征间的相似度关系，将其与特征提取网络联合训练，自适应地根据输入的特征调整度量方式。

由图2 的ⅠSNN 模型结构可知，关系度量网络首先通过卷积层C2 和C3 对输入的两个维度为16×110的特征向量f(Xi)和f(Xj)进行处理，输出为16×26 的特征图。为了减少模型参数，缓解过拟合问题，本文采用全局均值池化（global average pooling，GAP）[28]即P2 代替多层全连接。GAP 的基本思想是计算每个特征图的平均值，并用它来代替整个特征图，且该过程不会产生需要优化的参数。如图5 展示了采用普通全连接方法和采用GAP方法的计算量对比。

图5 全连接层和全局均值池化对比Fig.5 Comparison of full connection layer and global mean pooling

从图5 可以看出，如果使用全连接方法将16 个26维的特征图映射成相似度值，共需要416 次参数计算，而GAP 方法只需要16 次运算。在网络最后利用Sigmoid 激活函数把相似度值变换到[0，1]中，计算相似度值的方法如式（5）所示：

式中，Ri,j表示第i个样本和第j个样本之间的相似度值，g(⋅)表示将特征向量映射为相似度值的关系函数，f(⋅)表示特征提取网络的输出，Sigmoid是激活函数。

为了准确地度量易混淆类样本之间的相似度，定义了带权重的相似性损失函数，根据不同故障类之间区分的难易程度增加了惩罚系数，在容易混淆的故障类之间增大误判损失，损失函数如式（6）所示：

式中，LS表示相似度损失，Yi,j表示两个样本间的相似度标签，αi,j表示样本i和样本j属于不同故障种类时的惩罚系数。当两个样本不相似时，如果网络输出的Ri,j值不趋近于0，便给αi,j赋予较大数值来增加损失。

2.1.3 故障分类网络

由于关系度量网络只用到了样本的相似度标签，且只能判断成对样本的相似性，无法直接对待测数据进行分类，因此本文在ⅠSNN 模型中引入了分类网络。设计的故障分类网络能够利用每个样本自身的类别标签信息进行监督学习，可以直接预测出其属于哪个故障类别，增加了模型的灵活性。如图2 所示，故障分类网络与关系度量网络结构类似，首先利用卷积层C4 和C5将尺寸为16×110的特征向量映射为16×26的低维特征，然后通过全局均值池化层P3 以及全连接层F2 输出为5 种类别，最后在网络尾部使用Softmax 激活函数输出各个故障类的预测概率。网络训练时将两个样本特征f(Xi)、f(Xj)输入故障分类网络分别进行预测，而在测试阶段只需要输入一个待测样本。本文使用均方误差作为分类网络的损失函数，如式（7）所示：

式中，LC表示分类损失，Y(⋅)表示样本的故障类别标签，y(⋅)表示网络的预测标签，它的计算方法如式（8）所示：

式中，h(⋅)是分类网络的输出，Softmax是激活函数。

在ⅠSNN 故障诊断模型中，特征提取网络主要是对输入样本(Xi,Xj)进行初步特征提取；关系度量网络利用相似度信息对网络训练进行约束，使同类样本的特征距离变近，不同类样本的特征距离变远；分类网络则是完成最后的故障样本分类任务。三个网络相互约束，在小样本条件下充分利用了故障数据的时域信息、频域信息、标签信息和样本的相似度信息，将度量学习思想应用到分类问题中，且整个模型采用了较浅的网络结构，有效控制了参数量大小。在模型训练时，同时优化相似度损失LS和分类损失LC，将二者合并，得到模型最终的损失函数如式（9）所示：

2.2 故障诊断流程

本文在提出的ⅠSNN 模型基础上，设计了一个滚动轴承故障诊断流程，具体包含数据预处理、ⅠSNN模型训练和故障诊断三个步骤，如图6所示。

图6 滚动轴承故障诊断流程Fig.6 Process of rolling bearing fault diagnosis

（1）数据预处理

本文利用加速度传感器从故障诊断实验台采集滚动轴承的振动信号，将所采集故障信号的前半部分作为训练集，后半部分作为测试集。然后按照每2 000 个点为一段切分信号，并对切分后的每一段信号进行FFT变换得到对应的频域数据，将变换前后的数据进行串联拼接得到每个样本。

（2）ⅠSNN模型训练

首先对搭建好的ⅠSNN 模型进行参数初始化，每次从训练集中随机挑选出两个故障样本组成样本对共同输入模型，逐步训练特征提取网络、关系度量网络和故障分类网络。通过多次迭代最小化损失函数，并利用反向传播算法不断优化模型参数。当达到设定的最大训练次数后，保存模型参数。

（3）故障诊断

进行轴承故障诊断时，将测试集样本输入已经训练好的特征提取网络得到低维特征向量，然后通过分类网络输出故障诊断结果。

3 实验与分析

3.1 实验数据

为了验证本文提出算法的具体效果，从动力传动故障诊断试验台（drivertrain diagnostics simulator，DDS）采集5种不同健康状态的轴承振动信号作为实验数据，分别为正常状态、滚动体故障、内圈故障、外圈故障和复合故障（滚动体、内圈和外圈均发生损伤）。试验台的结构如图7所示，主要由驱动电机、齿轮箱、制动器和负载等部分组成。图8为除正常状态外的4种故障轴承的实物展示，红色框内标注的字母表示轴承所属的故障类型。

图7 动力传动故障诊断试验台Fig.7 Drivertrain diagnostics simulator

图8 轴承的4种故障状态Fig.8 Four fault states of bearing

为了模拟工程实际中有时难以采集到多种工况下丰富的故障数据，实验仅采集了一种工况的轴承故障信号作为训练数据。设置电机转速为1 700 r/min，负载电压为4 V，使用单向加速度传感器获取振动信号，采样频率设置为20 kHz，仅采样20 s。每种故障轴承的振动信号文件中共包含409 600 个采样点，将前10 s 的数据作为训练集，后10 s数据作为测试集。本文对采集到的轴承信号按照每2 000 点为一段进行不重叠切分，最终每类故障得到100个训练样本和100个测试样本。为了研究不同数量的故障样本对ⅠSNN 模型效果的影响，从每类100个训练样本中分别随机挑选了10个、20个、50个样本构造了4 种训练集。此外，为了后续验证ⅠSNN 的泛化性能，采集了另外两种工况的故障信号用来测试模型效果。一种工况与训练数据的工况相近（电机转速1 700 r/min，负载电压8 V），另一种工况与训练数据的工况差别较大（电机转速3 400 r/min，负载电压8 V）。测试数据的采样时间为10 s，样本切分方式与之前相同。本文所用数据集的划分如表1所示。

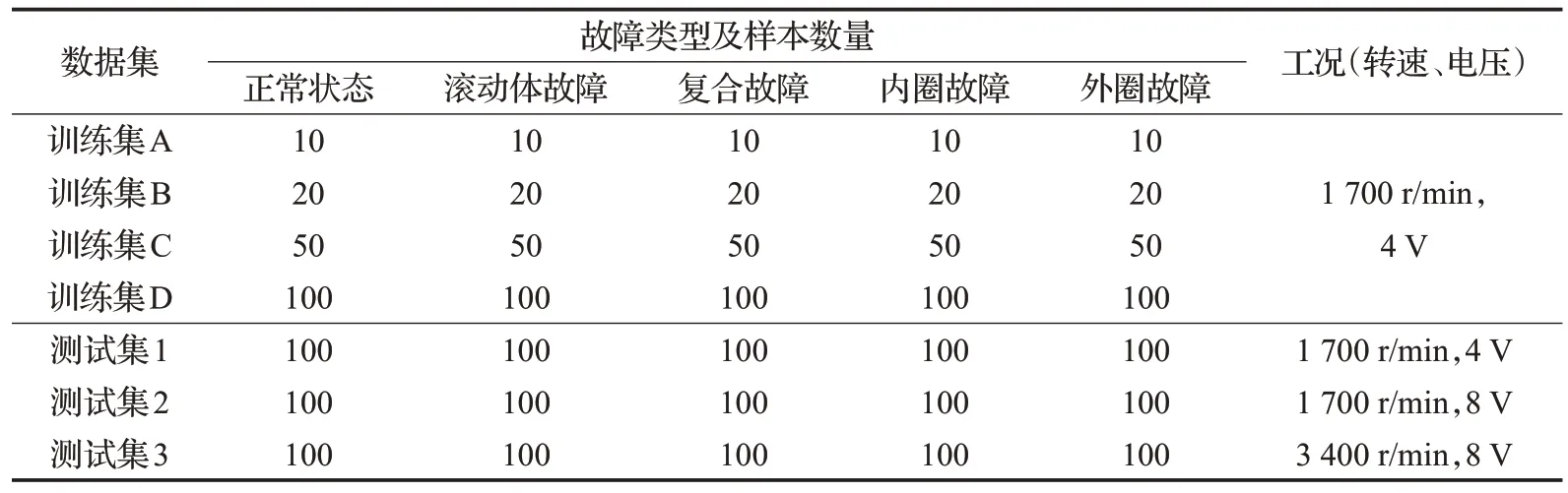
表1 实验数据集Table 1 Experimental datasets

3.2 实验参数设置

实验平台为i7-4790 CPU，英伟达GTX1050Ti，python3.7，Pytorch1.3。实验中采用Adam算法优化模型参数，Batch-size设置为50，学习率设置为0.002，最大迭代轮数为500次。本文所提ⅠSNN模型的参数设置如表2 所示，输入网络前需要将故障信号调整为40×100 维度，其中40 表示LSTM 的单时序输入尺寸，100 表示输入的时序总数。表2中，一维卷积的参数分别表示输入通道、输出通道、核尺寸、步长和padding的大小，池化层参数分别表示池化窗口大小和步长。

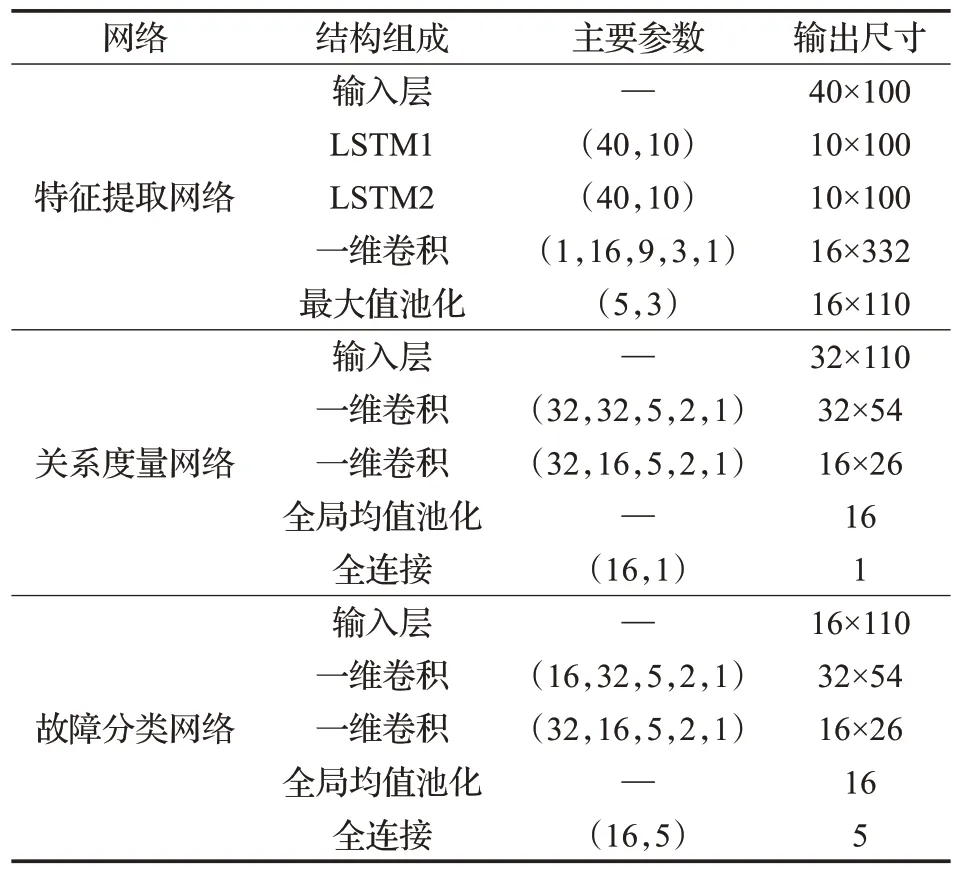
表2 ⅠSNN模型的参数设置Table 2 Parameters setting of ⅠSNN

3.3 ISNN算法性能分析

3.3.1 训练样本数量对模型性能的影响

本文的研究目的是提升小样本条件下的轴承故障诊断准确率，为了验证不同数量的训练样本对ⅠSNN 模型故障诊断性能的影响，设置每类训练样本数量分别为10、20、50、100 个，即采用表1 中的训练集A、训练集B、训练集C和训练集D作为训练数据，用测试集1验证模型效果。为了消除实验结果的随机性，进行多次重复实验，表3 记录了测试结果的平均准确率和标准差，具体计算方法如公式（10）、（11）所示：

表3 ⅠSNN模型在不同训练集下的诊断准确率Table 3 Diagnosis accuracy of ⅠSNN under different training sets 单位：%

由表3可知，随着训练样本数量的增多，ⅠSNN模型的故障诊断准确率不断提高。在每类故障仅有10个样本的情况下（训练集A），都能够获得83.6±2.6%的诊断准确率；当每类有50 个训练样本时（训练集C），准确率已经超过95%；当训练样本达到100个时（训练集D），平均准确率接近99%。此外，诊断准确率的标准差随着训练样本数量的增多从2.6%逐渐降低到0.6%，模型的训练结果更加趋于稳定。以上结果表明ⅠSNN模型对大规模训练数据的依赖性显著降低，在仅有几十个故障样本情况下仍然能取得较好的诊断效果。

3.3.2 不同特征提取网络对模型性能的影响

为了分析ⅠSNN模型中特征提取网络对故障诊断性能的影响，对比了4 种不同的特征提取方式，分别为只使用时域数据作为模型输入，只使用频域数据作为模型输入，只使用全连接层和只使用一维卷积搭建特征提取网络。在不同训练集下测试了各种特征提取方式的诊断准确率，结果如图9所示。

图9 不同特征提取方式的诊断准确率Fig.9 Diagnosis accuracy of different feature extraction methods

从图9可以看出，直接使用时域数据进行模型训练时（橙色柱），故障诊断效果最差。每类故障有10 个样本时，准确率仅有43.4%，当训练样本达到100 个时，也只能获得63.2%的准确率。与之相比，将频域数据输入模型进行训练（灰色柱），诊断效果得到明显改善。在10个训练样本情况下，准确率超过了80%，在100 个训练样本情况下准确率达到95.2%，比时域数据情况提升了32%，表明在故障诊断中，信号的频域信息能为模型提供更多的有效特征。此外，当使用不同的网络结构进行特征提取时，在训练样本数量特别少的情况下，卷积结构的特征提取效果（蓝色柱）还不如全连接结构的效果（黄色柱），例如仅有10个和20个训练样本时，采用卷积结构的准确率分别比采用全连接结构的准确率低了4.8个百分点和2.2 个百分点。随着训练样本数量的增多，卷积结构的特征提取效果越来越好，在每类有100个样本的情况下，故障诊断准确率超过了97%，明显好于全连接结构，表明了卷积网络对样本数量的依赖性。相比之下，采用本文设计的特征提取网络（绿色柱），即将故障信号的时域信息和频域信息一起输入模型，并利用LSTM和CNN结构联合提取样本特征，可以取得更好的故障诊断效果，在不同数量的训练样本下，都能取得最高的诊断准确率。

3.3.3 不同关系度量方式对模型性能的影响

为了分析ⅠSNN模型中关系度量网络对故障诊断性能的影响，在本文算法框架下，将网络度量方式替换为欧式距离和余弦距离，利用不同的训练数据集对3种方法的效果进行了验证，准确率结果如图10所示。

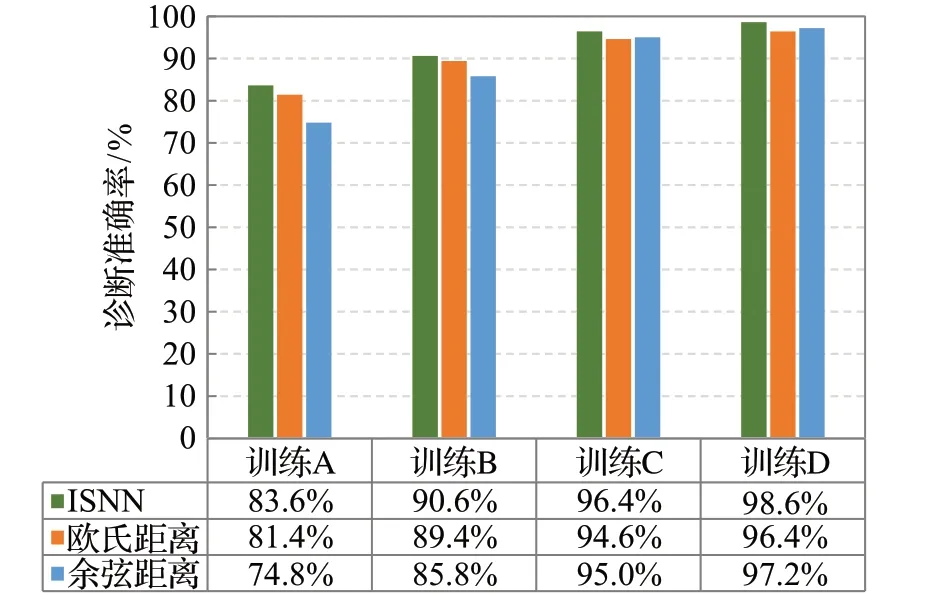
图10 不同关系度量方式的诊断准确率Fig.10 Diagnosis accuracy of different relationship measurement methods

从图10 可以看出，在本文的算法框架下，3 种关系度量方式均能取得较高的诊断准确率，但在各种训练集下也有所差别。具体而言，在每类10 个训练样本情况下（训练集A），余弦距离度量方式效果最差（蓝色柱），只有74.8%的准确率，而本文网络度量方式（绿色柱）的准确率为83.6%，比欧式距离度量方式（橙色柱）高2.2个百分点。但随着训练样本数量的增多，余弦距离度量方式的效果逐渐好于欧式距离度量方式，当每类有100个训练样本时（训练集D），前者的诊断准确率达到97.2%，高于后者96.4%的准确率，此时网络度量方法的准确率为98.6%，略高于两种固定的距离度量方式。综合来看，在训练样本量从10 个增加到100 个情况下，网络度量方法的效果和稳定性要好于固定的距离度量方法。

3.4 与其他方法效果对比

为了进一步验证ⅠSNN模型对小样本轴承故障诊断的优秀效果，选取未改进的孪生网络、原型网络[29]以及文献[30]中的卷积神经网络（1D-CNN）、深度置信网络（deep belief network，DBN）和自动编码器（auto-encoder，AE）作为对比方法。实验分别在4种训练集下对各个模型进行训练，为了验证模型的泛化性能，采用3 种不同工况的测试集进行测试。

3.4.1 相同工况下诊断准确率对比

表4列出了在不同训练样本数量下，各种方法在测试集1（与训练集工况相同）上的故障诊断准确率。可以看出，在训练样本数量特别少的情况下（训练集A），1D-CNN 的准确率最低，不到50%，原型网络和孪生网络两种小样本方法的准确率也只有60%左右，DBN 方法表现较好，准确率为76.8%，而本文提出的ⅠSNN方法在每类10个样本时也可以达到83.6%，远高于其他5种方法。当每类有50个训练样本时（训练集C），1D-CNN的准确率明显提高，达到88.6%，高于原型网络的82.5%和孪生网络的75.8%，DBN方法的准确率为91.8%，但仍然比ⅠSNN 方法低了近5%。当训练样本达到100 个时（训练集D），大部分方法都已表现很好，DBN 和AE 的准确率分别达到了97.1%和95.4%，明显高于原型网络和孪生网络，与ⅠSNN 方法的差距也变得更小。整体来看，单一的1D-CNN 模型受训练样本数量的影响较大，样本严重不足时会引起模型过拟合，直接用于小样本故障诊断效果并不理想。在各对比方法中，DBN 方法表现最好，改进前的孪生网络故障诊断效果很差，甚至不如原型网络，在100个训练样本的情况下，仅有86.7%的准确率，而改进后的ⅠSNN方法准确率得到显著提升，诊断效果明显好于其他几种对比方法。

表4 各种方法在测试集1上的准确率对比Table 4 Accuracy comparison of various methods on testing set 1单位：%

为了观察6种方法对每类轴承故障的识别情况，以每类20 个训练样本（训练集B）为例，绘制了各种方法在测试集1 上诊断结果的混淆矩阵，如图11 所示。其中横坐标表示预测的故障类型，纵坐标表示真实故障类型，主对角线为预测正确的样本数，每类共有100 个测试样本。

图11 各种方法在训练集B上诊断结果的混淆矩阵Fig.11 Confusion matrix of diagnosis results of various methods under training set B

从图11 可知，在每类故障有20 个训练样本的情况下，5种对比方法均产生了不少错分情况，故障诊断效果较差，而本文的ⅠSNN 方法则明显好于对比方法。具体来说，从图11（a）可以看出，用1D-CNN 进行诊断时，只有内圈故障和正常类样本被分得较好，而被测试的100个复合故障样本中仅有37 个被预测正确。图11（b）和（c）表明DBN 和AE 的效果好于其他对比方法，对各类故障都能正确分类80个左右。从图11（d）和（e）可以看出，原型网络的故障分类情况相比于1D-CNN有了一定程度的改善，孪生网络的诊断效果最差，仅对正常类轴承分得较好，有94个样本被识别正确，而复合故障和外圈故障有大约一半的样本被错分。相比之下，从图11（f）可以看出，本文的ⅠSNN 方法能显著改善各类故障的错分情况，除了复合故障被错分较多（有19个样本预测错误），其余故障类型均有90 个以上的样本被正确识别。以上分析表明，在训练样本较少的情况下，几种对比方法均难以对轴承故障进行有效诊断，而提出的ⅠSNN 方法能够有效提升故障诊断效果，实现小样本情况下的轴承故障诊断。

3.4.2 不同工况下诊断准确率对比

生产实际中，设备的运行工况往往会发生改变，导致要测试的故障数据与训练数据分布不一致，为了验证ⅠSNN 方法相比于其他方法对不同测试数据的泛化性能，使用表1 中的测试集2（与训练集工况相近）和测试集3（与训练集工况差别大）对4种方法的故障诊断效果进行验证，结果如表5所示。

表5 各种诊断方法在不同工况下的准确率对比Table 5 Accuracy comparison of various diagnostic methods under different operating conditions 单位：%

从表5 可以看出，对相近工况的数据（测试集2）进行诊断时，5种对比方法在10个样本（训练集A）和20个训练样本（训练集B）情况下的诊断效果都较低。当训练样本增加到100 个时（训练集D），1D-CNN、DBN 和AE 方法的准确率都达到90%以上，而原型网络和孪生网络的准确率分别只有74.4%和78.5%。此时ⅠSNN 方法的准确率仍然能保持在98%左右。当对工况变化较大的数据（测试集3）进行诊断时，对比方法的故障诊断效果变得更差，尤其是在训练样本不足50个的情况下，原型网络和孪生网络的诊断准确率仅有60%左右，另外三种对比方法也只有大约85%的准确率，而ⅠSNN 方法仍然能达到90%以上。通过以上分析可以得出，原型网络和孪生网络在面对变工况数据时诊断准确率变得很差，泛化能力很弱，1D-CNN、DBN 和AE 方法的准确率也有不同程度的下降，而ⅠSNN 方法在相近工况下准确率仅降低了1个百分点左右，在工况变化较大时也能取得最高95.2%的准确率，模型的泛化性能相较于其他5种方法有了明显提升。

为了更直观地展示ⅠSNN方法在小样本条件下对变工况数据的故障诊断效果，以训练集C（每类50个样本）和测试集3（与训练集工况差别大）为例，选择各种模型中诊断效果最好的DBN 方法作为对比，将两种方法的故障分类结果进行降维可视化，结果如图12所示。

图12 DBN和ⅠSNN方法在训练集C上的诊断结果可视化Fig.12 Visualization of diagnosis results of DBN and ⅠSNN under training set C

从图12（a）可以看出，DBN方法虽然能够将各个故障类大致分开，但彼此之间仍有不同程度的重叠，例如内圈故障（黄色）的部分样本混合到了其他多种故障中，正常类故障（红色）也有少量样本被误分到了滚动体故障（蓝色）中。此外，有大量外圈故障（紫色）和复合故障样本（绿色）相互重叠，模型的整体分类结果较差。从图12（b）可以看出，采用ⅠSNN 方法进行故障诊断后，相同故障类别的样本更好地聚集在了一起，不同类别样本之间也有较大间隔，区分明显，仅有少量的外圈故障样本（紫色）被错分到复合故障样本（绿色）中，表明ⅠSNN 方法在工况变化较大的情况下仍然能较好地识别各类轴承故障，验证了模型在小样本条件下良好的泛化效果。

4 结论

本文提出一种小样本条件下基于改进孪生神经网络（ⅠSNN）的滚动轴承故障诊断算法，将度量学习思想和普通分类网络集成到一个框架中，通过联合训练特征提取网络、关系度量网络和故障分类网络实现对轴承故障的精确诊断。经过大量实验分析，可以得出以下结论：

（1）ⅠSNN 模型在多种小样本情况下均能实现对轴承故障的有效诊断，当每类只有10个训练样本时，仍然能取得83.6±2.6%的准确率，当每类有100 个训练样本时，准确率可以达到98.6±0.6%。

（2）本文设计的LSTM+CNN 特征提取网络和利用神经网络进行关系度量的方式能够使模型学习到更具判别性的样本特征，从而获得更高的诊断准确率。

（3）通过与1D-CNN、DBN 和原型网络等方法的实验对比可知，本文提出的ⅠSNN 方法在小样本条件下具有更高的故障诊断准确率，当测试数据工况发生变化时也能表现出更好的泛化性，100个训练样本下可以达到95.2%的准确率。