面向ICS不平衡数据的重叠区混合采样方法

高 冰，顾兆军，周景贤，隋 翯

1.中国民航大学 信息安全测评中心，天津 300300

2.中国民航大学 计算机科学与技术学院，天津 300300

3.中国民航大学 航空工程学院，天津 300300

工业控制系统（industrial control system，ⅠCS）是能源、交通、城市公用设施等国家关键基础设施的重要组成部分[1-3]。信息技术与工业生产的深度融合，拓宽了ⅠCS 的发展空间[4]，但融合发展的同时也带来了复杂严峻的网络安全威胁[5]。典型ⅠCS安全保障体系可分为防护、检测、响应和恢复四个层次[6]，其中检测尤为关键，其负责识别企图破坏系统完整性、机密性以及可用性的行为，并为系统响应提供了必要的反馈[7-8]。

ⅠCS 数据大多存在着不平衡性，同时不平衡的ⅠCS数据普遍存在着类重叠现象。相关研究表明，数据的不平衡性并非是导致检测困难的唯一因素，当类别间的可分性较强且数据量足够多时，即使数据的不平衡程度很高，也并不需要太复杂的模式来区分各类样本[9]。不平衡问题在孤立状态下可能不会造成分类器性能明显下降，但当不平衡数据中存在着较为严重的数据重叠时，分类器的性能将受到很大影响[10-11]。

针对不平衡数据的检测问题，目前常采用平衡数据类别或检测数据重叠的策略[12]。

在平衡数据类别的策略中，常采用过采样、欠采样或混合采样方法。其中，Pan等人[13]提出了基于合成少数类过采样（synthetic minority over-sampling technique，SMOTE）[14]的方法，通过线性插值合成不平衡数据中的少数类样本使数据达到平衡状态。该方法提高了分类器对异常数据的学习能力，缓解了随机过采样的过拟合问题[15]，提高了检测性能。Agustianto 等人[16]提出了基于邻域清洗规则NCL（neighborhood cleaning rule）的欠采样方法，通过寻找某个样本的k个近邻，若该样本类别与k个近邻的类别不一致则删除属于多数类的样本或近邻。该方法能够达到平衡样本的目的，并与决策树C4.5 分类算法结合达到了较高的准确率。郑建华等人[17]提出了一种级联过采样与欠采样的混合采样方法，通过利用高斯混合模型和SMOTE-Borderline1 进行二次过采样，并利用一次随机欠采样以平衡数据，最后该方法以随机森林为基分类器实现了较好的分类性能。上述方法均取得了一定的成效，但存在着一定的局限性，比如数据中噪声样本增加或所提方法对不同分类器的适配性较低等，而且没有考虑到不平衡数据中存在的数据类别重叠问题。

在检测数据重叠的策略中，常依据聚类或无监督分类模型来检测重叠并辅以欠采样方法对重叠多数类样本进行处理。对此，Vuttipittayamongkol 等人[18]基于软聚类算法提出了一种面向重叠的欠采样框架OBU（overlap-based under-sampling），该方法依据软聚类算法分配的样本成员度确定潜在的重叠样本，并将负类样本从重叠样本中剔除且无须平衡数据。Devi 等人[19]提出将多数类和少数类样本分别送入一类支持向量机OCSVM（one-class support vector machine）中进行检测，两类样本被检测出的离群点即为二者的重叠数据，同时选择Tomek-link 欠采样方法来消除重叠边界的多数类样本并平衡数据。Li 等人[20]提出先用少数类样本训练异常检测模型，然后将原始数据输入模型中以排除少数类的异常值和大量的多数类样本，剩余数据形成重叠子集，并运用欠采样方法剔除该子集中的多数类样本，最后将重叠与非重叠子集合并以训练分类器。上述方法均不同程度上优化了数据分布、改善了分类器的学习能力，相比于平衡数据类别的方法在处理不平衡数据上具有独特优势，但同时也存在着重叠识别率较低或没有考虑到重叠数据中多数类样本的数据清洗以及少数类样本的采样问题等。

本文针对ⅠCS异常检测中存在的数据不平衡问题，从类重叠的角度出发，提出了一种面向重叠区域的混合采样方法：OverlapRHS（overlap region with hybrid sampling）。该方法基于分而治之的思想，分别利用多数类样本和少数类样本训练支持向量数据描述SVDD（support vector data description）[21]以构建重叠检测模型，并在此基础上合成重叠数据区域的少数类样本，增强少数类样本的数据特征，然后对该区域的多数类样本进行邻域清洗以削弱分类器在训练时偏向于多数类样本。本文通过将OverlapRHS 与支持向量机、逻辑回归、k-近邻、决策树分类器进行组合，在公开的3个ⅠCS数据集和1 个入侵检测数据集上进行了测试，并对比了其他4 种处理不平衡问题的采样方法。结果表明，OverlapRHS 在数据重叠检测、混合采样以及对分类器训练效果提升方面均展现出了有效性，分类器的检测性能与泛化能力得到了显著提升，并且该方法明显优于其他处理不平衡数据的采样方法。

1 OverlapRHS概述

OverlapRHS分为两个阶段，如图1所示。第一个阶段是重叠区域检测阶段，第二个阶段是重叠区域采样阶段。OverlapRHS 的具体实施流程如下：不平衡数据集以8∶2 的比例被划分为训练集Xtrain和测试集Xtest，训练集Xtrain在经过重叠区域检测阶段时，首先依据其类标签将Xtrain划分为多数类样本集Xmajor和少数类样本集Xminor，之后利用Xmajor和Xminor分别训练SVDDmajor和SVDDminor，由此得到两个不同的决策函数Fmajor(xi)和Fminor(xi)，然后计算训练集Xtrain中的所有样本分别在两个决策函数上的函数值，最后根据函数值以及相关预定规则判断训练集Xtrain中样本点的分布情况。

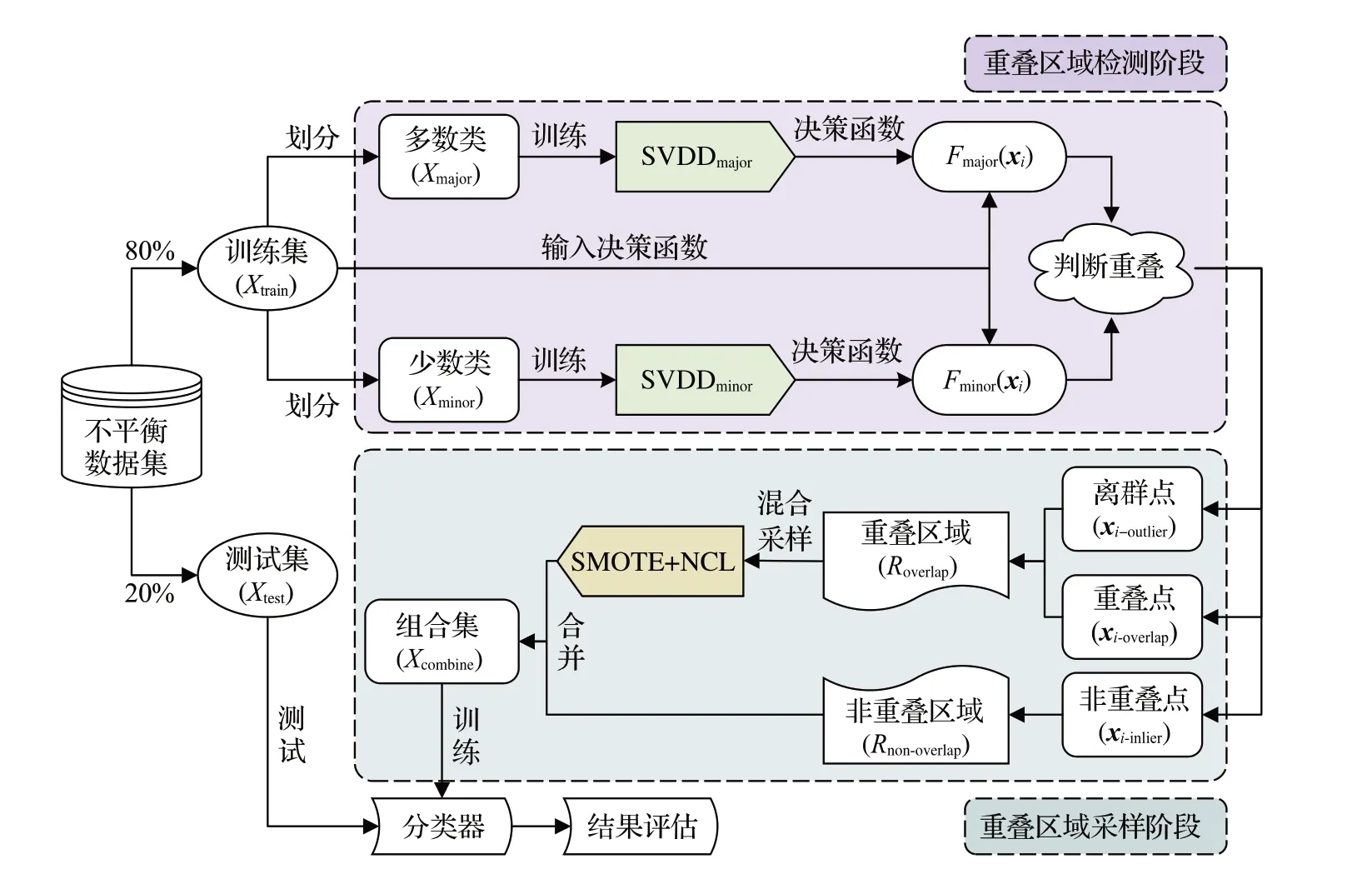
图1 OverlapRHS方法结构图Fig.1 Structure diagram of OverlapRHS method

在重叠区域采样阶段中，重叠区域Roverlap由离群点xi-outlier和重叠点xi-overlap共同构成，非重叠区域Rnon-overlap仅由非重叠点xi-inlier构成。在重叠区域Roverlap内加入离群点xi-outlier主要是考虑在后续采样过程中可以生成多样化的少数类样本，以及在最大限度保留整体多数类信息的情况下剔除更多的多数类样本。在确定重叠区域Roverlap之后，通过融合SMOTE合成少数类过采样和NCL邻域清洗规则以完成该区域内的混合采样工作，非重叠区域Rnon-overlap则不做采样处理。最后将重叠区域Roverlap混合采样之后的所有样本与非重叠区域Rnon-overlap内的所有样本合并得到组合样本训练集Xcombine，并用其训练分类器，最后使用测试集Xtest在训练好的分类器上进行测试评估。下面将对OverlapRHS两个阶段的内容作详细阐述。

1.1 重叠区域检测阶段

重叠区域检测阶段结构示意图如图2 所示。根据训练集Xtrain所划分的多数类样本集Xmajor和少数类样本集Xminor分别在SVDDmajor和SVDDminor上构建最小超球，并利用所得到的最小超球半径Rmajor和Rminor设置相应的决策函数Fmajor(xi)和Fminor(xi)，最后依据重叠判断规则对训练集Xtrain中样本点的分布进行划分。

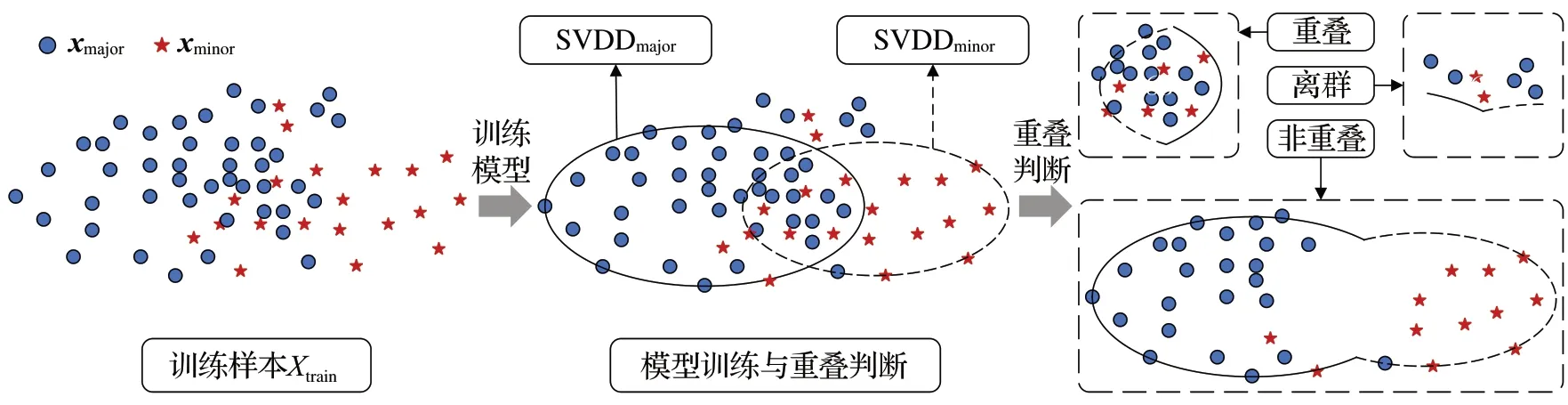
图2 重叠区域检测阶段结构示意图Fig.2 Structure schematic diagram of overlap region detection stage

假定有数据集X={x1,x2,…,xn}，为了构造最小超球，同时为了更好地处理高维复杂数据的非线性映射问题，本文采用径向基函数核（radial basis function kernel，RBF核）作为高维特征空间映射函数K，将数据从原始空间Ok映射到特征空间Fk，并解决如（1）所示的优化问题：

其中，R>0 是超球半径，c∈Fk是超球球心，ξi≥0 是用于惩罚数据中噪声的松弛变量，其目的是防止模型出现过拟合，C是平衡超球半径和松弛变量的参数。

上述优化问题的约束条件可通过拉格朗日乘子法纳入优化问题（1）中，结果如公式（2）所示：

其中，拉格朗日乘数αi、γi≥0。利用L分别对超球半径R、超球球心c和松弛变量ξi求偏导，并将偏导数设置为0，有：当xi在Fmajor(xi)和Fminor(xi)上的决策函数值均大于或等于0，此时xi同时位于两个超球的内部或边界上，那么该点被定义为重叠点xi-overlap；当xi当且仅当在Fmajor(xi)或Fminor(xi)其中一个决策函数上的值小于0时，此时xi仅位于一个超球内部而位于另一个超球外部，那么该点被定义为非重叠点xi-inlier。

将公式（3）中得出的结果重新纳入公式（2）中，整理可得出最终的超球半径计算公式为：

1.2 重叠区域采样阶段

其中，xv∈SV，SV为支持向量集合，当xi满足约束条件‖xi-c‖2=R2时，有0<αi0的xi共同构成了支持向量集合SV。由公式（4）可以得出，对于待检测的样本，其距超球球心的距离公式为：

由公式（4）和公式（5），本文通过设定如公式（6）的决策函数来检测样本的分布情况：

即，如果F(xt)>0 ，那么样本xt位于超球内部；如果F(xt)=0，那么样本xt位于超球边界上；如果F(xt)<0，则样本xt位于超球外部。

在SVDDmajor和SVDDminor均训练完毕之后，将训练集Xtrain中的所有样本分别输入至决策函数Fmajor(xi)和Fminor(xi)中，并根据Fmajor(xi)和Fminor(xi)所得出的决策函数值，判断Xtrain中样本点的分布情况，判断规则如下：

（1）if(Fmajor(xi)<0) and (Fminor(xi)<0):xi→outlier

（2）if(Fmajor(xi)≥0) and (Fminor(xi)≥0):xi→overlap

（3）if[(Fmajor(xi)<0) and (Fminor(xi)≥0)]or[(Fmajor(xi)≥0) and (Fminor(xi)<0)]:xi→inlier

简述之，即有样本点xi∈Xtrain，当xi在Fmajor(xi)和Fminor(xi)上的决策函数值均小于0 时，此时xi同时位于两个超球外部，那么该点被定义为离群点xi-outlier；

重叠区域采样阶段结构示意图如图3 所示。首先利用SMOTE对所确定的重叠区域Roverlap内的少数类样本进行线性插值过采样，其目的是增大少数类样本对分类器的可见性，同时避免大量的生成样本嵌入至非重叠区域Rnon-overlap内多数类样本的数据空间中，以防止在样本生成时加剧整体数据的类别重叠。在此基础上，利用NCL对过采样之后重叠区域Roverlap内的多数类样本进行邻域清洗，其目的是缓解整体数据的不平衡，降低数据重叠程度，削弱分类器偏向于多数类样本的趋势，进一步增大少数类样本的可见性。下面将对重叠区域采样阶段的过采样和欠采样两部分内容作更进一步的论述。

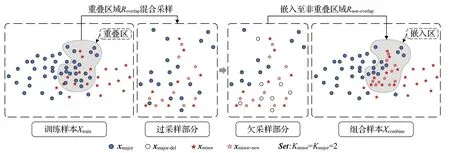
图3 重叠区域采样阶段结构示意图Fig.3 Structure schematic diagram of overlap region sampling stage

1.2.1 过采样部分

在过采样部分，利用SMOTE 对该区域内的少数类样本进行过采样，过程如下：

首先依据欧式距离（euclidean distance，ED）计算出Roverlap区域内每个少数类样本xminor到此区域内其他少数类样本xminor-rest的距离，如公式（7）所示：

之后依据式（7）所得到的结果，选取距离xminor最近的Kminor个近邻，根据经验与实验验证，文中Kminor设置为5。对于每个少数类样本xminor，从其Kminor个近邻中随机选择a个近邻，对于选出的每一个近邻xa，其与xminor以如下方式构建新的少数类样本：

其中，Nrand为0 至1 间的随机数，Vdiffer为少数类样本xminor与其近邻xa差的绝对值，新的少数类样本xminor-new则由xminor、Nrand和Vdiffer插值构建。在处理完每一个少数类样本之后，将构建的所有新样本xminor-new嵌入至重叠区域Roverlap内。至此，过采样部分完成。

1.2.2 欠采样部分

在欠采样部分，利用NCL 清理过采样之后重叠区域Roverlap内的部分多数类样本，过程如下：

同样依据欧式距离计算出Roverlap区域内每个多数类样本xmajor到此区域内其他多数类样本xmajor-rest的距离，如公式（9）所示，并依据结果选取每个多数类样本xmajor的Kmajor个最近邻，为了避免多数类样本信息丢失过度，经验证，本文中Kmajor以4为宜。

然后对于该区域内的每个多数类样本xmajor，以如下规则进行领域清洗：

其中，为xmajor的Kmajor个近邻中多数类样本的个数，即如果xmajor的Kmajor个近邻中有超过半数的样本都不属于多数类样本，那么该样本将被标记为xmajor-del。在处理完Roverlap区域内的全部多数类样本之后，所有标记为xmajor-del的多数类样本将从该区域中剔除。至此，欠采样部分完成。

完成重叠区域Roverlap的混合采样之后，将该区域内的所有样本与非重叠区域Rnon-overlap内的所有样本合并为组合样本集Xcombine作为最终的训练集来训练分类器，如公式（10）所示，最后用测试集Xtest进行测试。

2 实验与结果分析

2.1 数据集与实验设计

实验所用的3 个公开ⅠCS 数据集分别是：BHP（burst header packet）为光突发交换网络中多控制分组存在洪泛攻击的数据集[22]；GP（gas pipeline）为天然气管道传感器数据集[23]；Power 为电力输电系统数据集[24]。同时使用1个入侵检测数据集NSLKDD[25]作为实验对比。表1 所示为4 个数据集的基本信息：数据集名称、数据量、特征维数，多数类个数，少数类个数和不平衡率Imb。Imb计算公式如下所示：

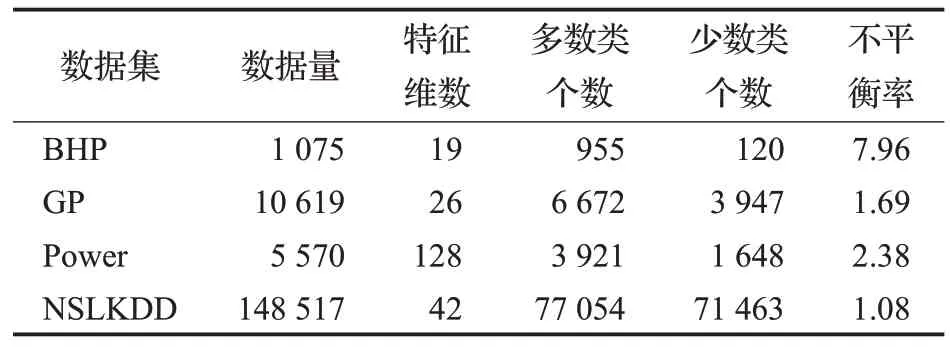
表1 数据集基本信息Table 1 Basic information of datasets

其中，Nmajor是多数类个数，Nminor是少数类个数，Imb值越大，表明数据不平衡程度越高。

实验所用评估指标有准确率（accuracy，Acc）、精确率（precision，Pre）、召回率（recall，Rec）、F1 分数（F1-score，F1）以及G-mean值。

其中G-mean值是评估正类召回率和负类召回率的综合指标，其求解公式如下所示：

其中，TP表示被正确预测为正类的正样本数，FP表示被错误预测为正类的负样本数，TN表示被正确预测为负类的负样本数，FN是被错误预测为负类的正样本数。

实验所用对比采样方法有：NearMiss 欠采样方法、SMOTE 过采样方法、ADASYN 自适应抽样方法，以及跳过重叠检测阶段直接利用SMOTE 与NCL 对数据集进行重采样的SMOTE-NCL方法。

2.2 实验结果分析

2.2.1 重叠检测与混合采样效果分析

为了较为直观地展示OverlapRHS的重叠检测和混合采样效果，本文以BHP数据集为例，采用t-SNE[26]数据降维方法对OverlapRHS各阶段数据的大致分布情况进行可视化分析。设定t-SNE嵌入空间维数为3，为了确保嵌入空间的全局稳定性，嵌入初始化方法设为PCA[27]；○代表多数类样本，☆代表少数类样本；颜色的深浅程度代表着样本点的分布密度，颜色越深，说明该区域的样本密度越大，分布在该区域的相似样本越多。图4所示即为BHP数据集在OverlapRHS各阶段的数据分布情况。

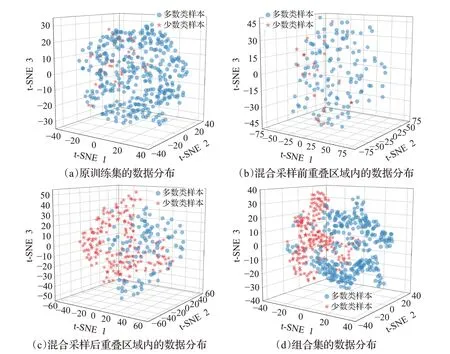
图4 BHP数据集在OverlapRHS各阶段的数据分布情况Fig.4 Data distribution of BHP dataset at each stage of OverlapRHS

图4（a）为原训练集的数据分布，其中少数类样本与多数类样本存在较大程度的数据重叠，分类边界模糊。图4（b）为所检测出来的重叠数据区域，该区域中大部分少数类分布于多数类样本的数据空间中，不过也存在着小部分少数类和部分多数类样本没有重叠的情况，这是因为重叠区域是由离群点xi-outlier和重叠点xi-overlap共同构成的，原因已在1.2节作出相关阐述。图4（c）中，重叠区域少数类样本在经过采样后，数据规模得到扩充，多数类样本在经邻域清洗后，与少数类样本的重叠降低。图4（d）中组合集相比于原训练集来说重叠程度减轻，不平衡程度缓解，少数类样本在数据得到增强的同时并没有大规模地侵入到多数类样本的数据空间中，且有较为明显的分类边界，分类器能更容易地学习到少数类样本的特征分布，说明OverlapRHS 在重叠检测和混合采样中具有有效性。

为了考证不同采样方法间的差异性，本文继续以BHP数据集为基准，利用t-SNE对比OverlapRHS与NearMiss、SMOTE、ADASYN以及SMOTE-NCL的采样效果。如图5所示即为各方法对BHP数据集采样后的数据分布情况。

图5 各方法在BHP数据集上采样后的数据分布情况Fig.5 Data distribution of BHP dataset after sampling by each method

图5（a）为OverlapRHS对数据集重叠区域混合采样后的数据分布，也即组合集的数据分布。在图5（b）中，NearMiss 的目的是剔除数据集中的多数类样本以达到类别平衡，但这会导致多数类样本的代表性不足，有效信息丢失，分类器准确性下降，而且没有缓解重叠问题。除NearMiss 外，图5（c）、（d）、（e）中的SMOTE、ADASYN 和SMOTE-NCL 均不同程度地扩展了少数类样本的数据规模，使少数类样本与多数类样本达到了平衡状态。但从三者的数据分布来看，虽然它们的数据类别得以平衡，但生成的少数类样本却大量地嵌入到多数类样本的数据空间中，加剧了数据集的重叠程度，并且大量的生成样本对分类器的训练过程也存在着潜在的过拟合风险。

表2 为4 个数据集经OverlapRHS 处理前后的数据不平衡率对比。由表可知，各数据集在经过OverlapRHS处理之后的不平衡率并没有达到平衡状态，这说明OverlapRHS与现有方法有所不同。OverlapRHS旨在检测出重叠数据，并在重叠数据区域内进行重采样，这一点在图4中得到验证，重采样数据不会对非重叠数据区域内的数据分布造成影响，并且能在一定程度上缓解整体数据的不平衡程度，而无须刻意谋求数据类别的最终平衡。

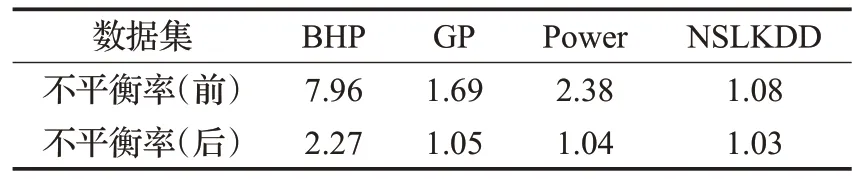
表2 各数据集经OverlapRHS处理前后的不平衡率Table 2 Ⅰmbalance rate of each dataset before and after OverlapRHS processing

2.2.2 OverlapRHS对分类器性能提升效果分析

为了检验OverlapRHS 对分类器性能的提升效果，实验选取支持向量机、逻辑回归、k-近邻、决策树分类器以及BHP、GP、Power、NSLKDD 数据集对其进行测试，通过对比各分类器在数据集原始无采样（origin）状态和经OverlapRHS处理后的状态上的准确率（Acc）、精确率（Pre）、召回率（Rec）和F1 分数（F1）对其进行评估。实验结果如图6~9所示。

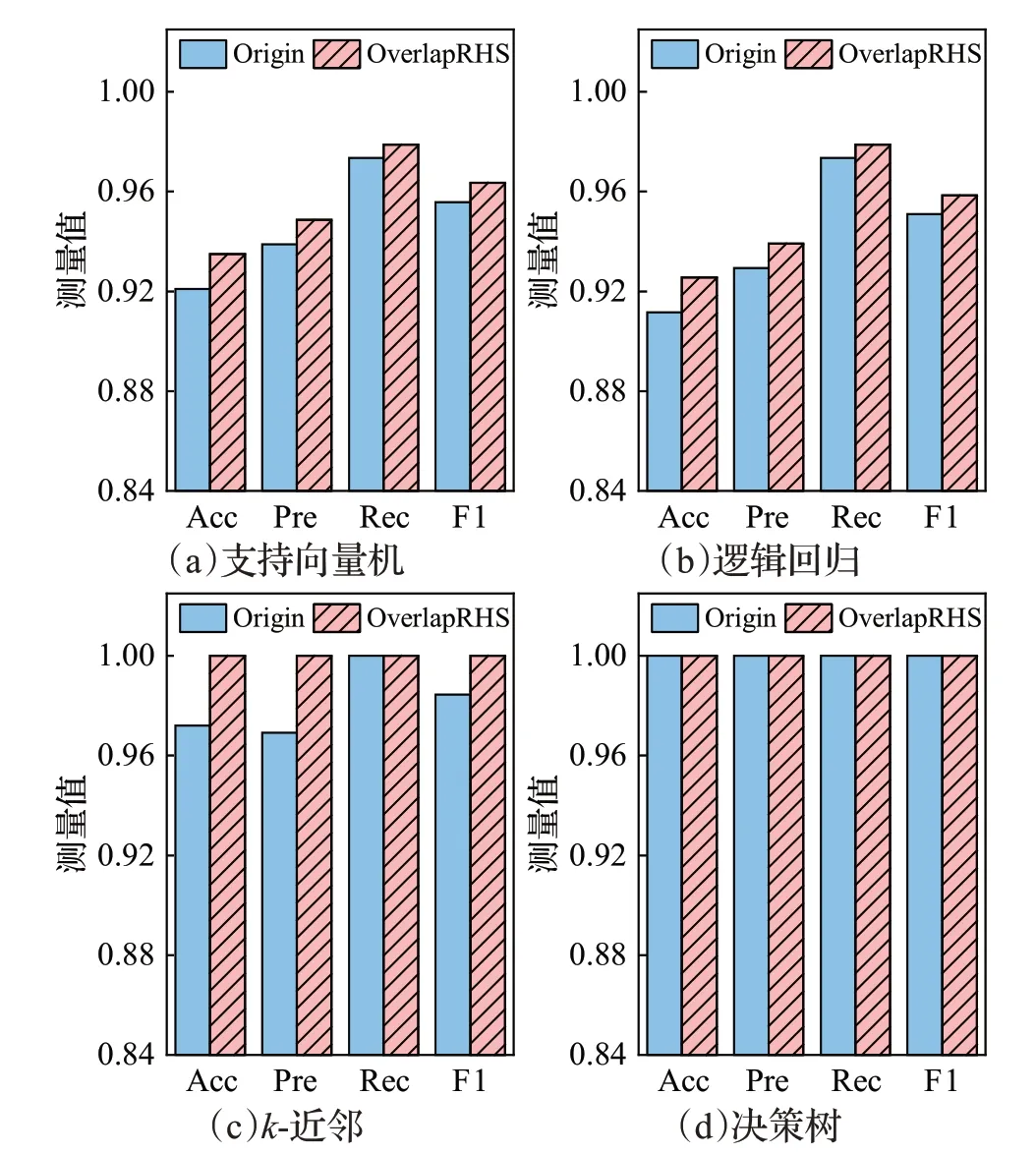
图6 BHP数据集上OverlapRHS对各分类器的性能提升对比Fig.6 Performance improvement comparison of OverlapRHS on BHP dataset for each classifier

如图6是BHP数据集上OverlapRHS对各分类器的性能提升对比结果。由图可知，支持向量机和逻辑回归在OverlapRHS 上的各项指标均有不同程度的提升，二者在OverlapRHS 上的准确率分别为0.934 9 和0.952 6，精确率分别为0.948 7和0.937 1，召回率均达到了0.978 8，F1 分数分别为0.772 6 和0.726 0。k-近邻在Origin 和OverlapRHS 上的召回率均为1，但OverlapRHS 在保持召回率为1 的情况下，将k-近邻的准确率、精确率和F1分数均提升到了1，体现了OverlapRHS 的不俗性能，有效检测出了BHP 数据集的重叠数据，再辅以混合采样显著提升了k-近邻的检测效果。最后，决策树在Origin和OverlapRHS 上的各项指标均为1，这一方面与BHP数据集的属性有关，其特征维数仅为19，维数越少，数据特征分布越简单，越易于分类器的学习，其次，BHP数据集的数据量也比较小，数据量越小，数据中存在的噪声数据就越少，从而对分类器性能影响越小；另一方面，决策树是基于树的分类器，自带正则项，能有效缓解过拟合问题。

如图7 是GP 数据集上OverlapRHS 对各分类器的性能提升对比结果。从整体上来看，OverlapRHS 对支持向量机和逻辑回归的性能提升比较有限，两个分类器在Origin 和OverlapRHS 上的召回率达到了一致的0.974 7，除此之外，OverlapRHS在支持向量机和逻辑回归的其余各项指标上仅提升了约0.04%~0.13%不等。从图中可以得知，k-近邻在OverlapRHS 上的各项指标均有不同程度的改善。对GP 数据集而言，OverlapRHS对决策树的性能提升最为明显，其将决策树的各项分类指标提升了约2.6%~3.8%，其中召回率达到了0.974 7。

图7 GP数据集上OverlapRHS对各分类器的性能提升对比Fig.7 Performance improvement comparison of OverlapRHS on GP dataset for each classifier

如图8 是Power 数据集上OverlapRHS 对各分类器的性能提升对比结果。首先需要说明的是，Power数据集虽然仅有较少的5 570 条数据，但是却具有高达128维的数据特征维度，一般情况下，数据集特征维度越高，数据特征分布越复杂，复杂的数据特征分布会对分类器的性能造成严重影响。本文所采用的支持向量机（线性核）和逻辑回归均是线性分类器，它们的分类决策面都是线性的，无法较好地拟合复杂的数据特征分布，从而导致分类效果较差。从图8（a）、（b）中可以很直观地看出，支持向量机和逻辑回归在Origin和OverlapRHS上的整体性能较低，特别是召回率和F1分数。但是，OverlapRHS依然展现出了效果，Power数据集在经过OverlapRHS处理之后，在支持向量机和逻辑回归上的各项指标均有提升，逻辑回归相较于支持向量机提升稍大。在非线性分类器上，k-近邻在OverlapRHS上的提升最为显著，其中召回率提升了约24.6%，F1分数提升了约15.7%，准确率和精确率也分别有5.9%和5.5%的性能改善。对决策树而言，其在OverlapRHS 上的精确率降低了约1%的性能，但在召回率上提升了约6.4%，准确率以及综合评价指标F1 分数都有所改观，在异常检测中，相较于精确率，召回率更加重要，较高的召回率能够减少系统漏报率，防止检测系统因遗漏攻击导致重大损失。所以，OverlapRHS 仅以损失些许精确率为代价，提升了召回率以及综合性能，进一步体现了OverlapRHS的优势。

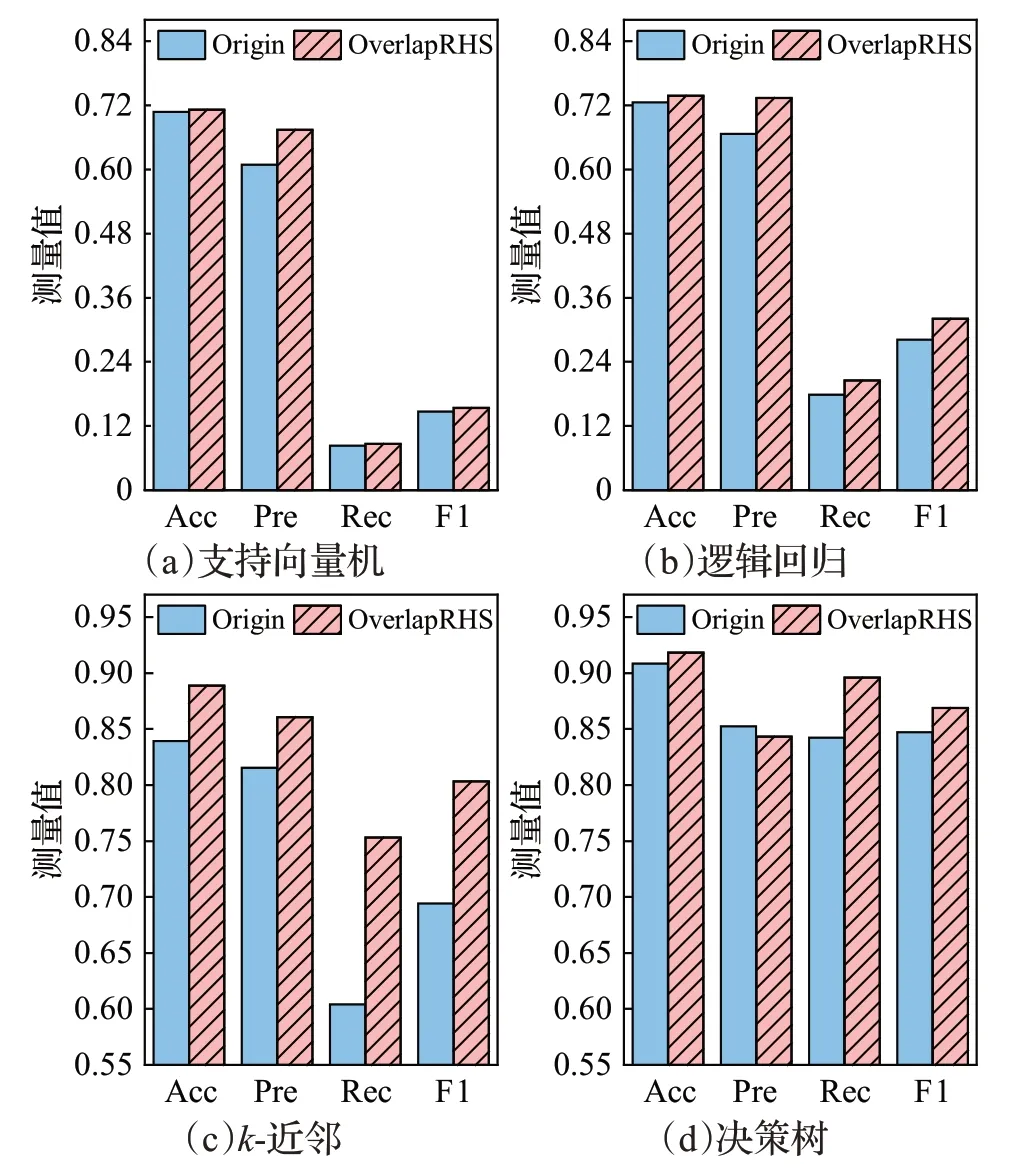
图8 Power数据集上OverlapRHS对各分类器的性能提升对比Fig.8 Performance improvement comparison of OverlapRHS on Power dataset for each classifier

如图9是NSLKDD数据集上OverlapRHS对各分类器的性能提升对比结果。由图可知，各分类器在Origin和OverlapRHS 上均达到了很高的召回率，这说明各分类器存在着较低的漏报率，但同时也说明NSLKDD 数据集中存在着大量具有相似特征分布的正类和负类样本，也即是存在较高的类别重叠，从而导致分类器无法有效学习各类数据特征，在面对负类样本时错误地将其归为正类，导致了高召回率、低精确率。前面提到，召回率对异常检测很重要，但是并不意味着精确率不重要，精确率较低会导致系统的误报率较高。从图中可以直观地看出，高召回率导致了各分类器存在着较低的精确率。但是NSLKDD 数据集在经过OverlapRHS 的优化之后，各分类器维持或略微提升了当前的高召回率，并且将各分类器的精确率提升了约2.9%~6.9%，准确率提升了约2.3%~6.1%，F1 分数提升了约1.6%~3.7%。可见，对于网络入侵检测领域的数据集，OverlapRHS依然展现出了不俗的数据优化能力。

图9 NSLKDD数据集上OverlapRHS对各分类器的性能提升对比Fig.9 Performance improvement comparison of OverlapRHS on NSLKDD dataset for each classifier

2.2.3 各采样方法对比结果分析

为了进一步探索OverlapRHS相较于其他处理类不平衡问题采样方法的有效性，实验以G-mean值为基准，它是评估数据各类别召回率的综合评价指标，并兼顾整体检测效果，G-mean 值越大，表明分类器的性能越好、漏报率越低。通过在每个数据集上分别计算支持向量机、逻辑回归、k-近邻和决策树分类器在NearMiss、SMOTE、ADASYN、SMOTE-NCL 以及OverlapRHS 方法上的G-mean 值，得到如图10 所示的对比结果，图中每个数据集为一个子图，横轴为不同的分类器，纵轴为各方法在每个分类器上的G-mean值。

图10 不同数据集下各分类器在不同方法上的G-mean值对比Fig.10 Comparison of G-mean values of each classifier on different methods under different datasets

观图可知，在图10（a）BHP 数据集中，OverlapRHS与其他4 种方法相比，在支持向量机上提高了约3.8%~10.9%。但在逻辑回归上相比于SMOTE-NCL 并未改善，但较其他3种方法提高了约1.9%~8.3%。其中OverlapRHS 在K-近邻上相比其他方法提升最为显著，约14.0%~28.2%。在决策树上，OverlapRHS 相较于SMOTE 和ADASYN 虽未改善，是因为它们的G-mean值均为1，不过与NearMiss 和SMOTE-NCL 相比却有约7.7%~17.0%的大幅提升，进而说明OverlapRHS 具有有效性。在图10（b）GP数据集中，OverlapRHS与SMOTE、SMOTE-NCL在支持向量机和逻辑回归上的G-mean值相差无几，性能差距不大，不过与NearMiss和ADASYN相比，OverlapRHS 分别提升了两个分类器约8.0%~14.5%和7.6%~14.5%的性能。OverlapRHS 在k-近邻和决策树上相比于4种对比方法均有改观，其中在决策树分类器上改进较为可观，相比各方法提升了约0.6%~24.6%。在图10（c）Power数据集中，各方法在各分类器上的G-mean值难分伯仲。由于数据集存在的高维复杂分布特性，且G-mean值较为关注各类别数据的召回率，所以导致线性分类器的G-mean值较低。整体来看，虽然OverlapRHS结合各分类器在Power数据集上的G-mean值与其他方法相比改进不太明显，甚至在k-近邻分类器上的G-mean 值略逊于NearMiss、SMOTE 和ADASYN，但在绝大多数情况下，OverlapRHS在复杂Power数据集上的表现依然略胜于其他方法。在图10（d）NSLKDD数据集中，可以看出，各分类器结合OverlapRHS 的G-mean 值均在不同程度上优于其他方法，相比于其他方法策略，在支持向量机上提升了约0.7%~10.5%，在逻辑回归上提升了约5.2%~6.9%，在k-近邻上提升了约1.8%~16.1%，在决策树上提升了约3.9%~9.8%，进一步展现了OverlapRHS的有效性与鲁棒性。

此外，从G-mean值角度考虑各分类器与OverlapRHS的搭配效果，纵观全局，在4个数据集上，k-近邻和决策树是与OverlapRHS 结合最好的两个分类器，二者整体的分类效果优于支持向量机和逻辑回归。这一方面与分类器特性有关，k-近邻和决策树是非线性分类器，能很好地学习数据特征间的非线性关系；另一方面体现了OverlapRHS能够很好地适应具有不同属性且特征分布较为复杂的数据集，并在不同数据集下展现了较之于其他采样方法的良好效果。

2.2.4 各采样方法计算代价分析

计算代价是所有采样方法需要考虑的重要因素之一，为了验证OverlapRHS的计算代价，本文从时间代价和空间代价两个角度出发，并以维数较高、数据特征分布较为复杂的Power 数据集和数据规模较大的NSLKDD数据集为基准，分析OverlapRHS 与NearMiss、SMOTE、ADASYN以及SMOTE-NCL方法之间的计算代价。

实验所用运行平台统一为Ⅰntel Core i7-7700HQ处理器，16 GB 内存。所得到的各采样方法在Power 和NSLKDD 数据集上的时间代价和空间代价结果分别如表3、表4 所示。表3 中，STC（sampling time cost）表示采样时间代价，单位为秒（s）。表4 中，SMC（sampling memory cost）表示采样空间代价，单位为兆字节（MB）。

表3 各采样方法的采样时间代价Table 3 Sampling time cost of each sampling method单位：s

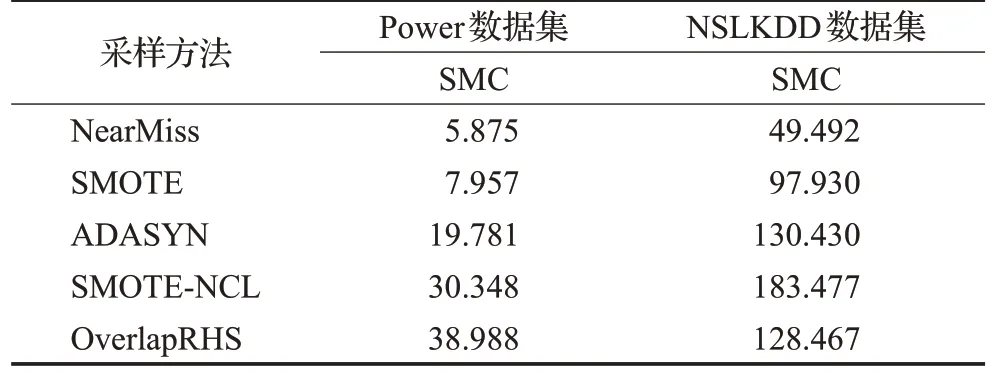
表4 各采样方法的采样空间代价Table 4 Sampling memory cost of each sampling method单位：MB

观察表3和表4可知，4种对比方法在两个数据集上的计算代价表现具有一般规律，即在时间和空间代价上，NearMiss 欠采样方法要低于其他3 种非欠采样方法，且混合采样方法的时间和空间代价最高。由于OverlapRHS 仅作用于重叠区域的数据，所以在表3 中，其在Power 数据集上的时间代价相比于SMOTE-NCL要有所降低，甚至在NSLKDD 数据集上的表现要优于耗时最低的NearMiss 方法；在表4 中，虽然OverlapRHS在Power数据集上的空间代价要高于其他方法，但在规模较大的NSLKDD 数据集上的空间代价却略低于ADASYN和SMOTE-NCL方法。

由上述分析可以得出，OverlapRHS 在采样效率方面相比于其他部分方法有一定的提高。此外，从数据集属性角度而言，数据特征分布的复杂与否以及数据规模的大小对于OverlapRHS的时间代价影响甚微；但OverlapRHS 空间代价的高低，相较于数据规模，更多地与数据特征分布的复杂程度有较大关系，即复杂的数据特征分布会加大OverlapRHS的空间占用。

3 结束语

本文针对工业控制系统异常检测中存在的数据不平衡问题，从类重叠角度出发，利用支持向量数据描述构建了重叠检测模型，并在此基础上提出了一种面向重叠区域的混合采样方法：OverlapRHS。

经实验验证，本文所提之方法，能够有效检测出不平衡数据的重叠数据，并通过对重叠数据区域施加混合采样，增强了分类器的学习能力，使之在检测精度、召回率等指标上均得到了不同程度的提升，并且普遍优于其他处理不平衡数据的采样方法。未来的工作将研究如何运用生成对抗网络在重叠数据区域生成高质量的少数类样本，以防止插值采样带来的潜在过拟合风险；以及针对特征分布较复杂的数据进一步优化方法结构，以缓解计算资源的占用。