共直角顶点的两个相似直角三角形结构的拓展及思考

陈磊

摘 要：几何模型及其二级结论在中高考中屡次出现．本文通过在七年级期末复习时一个压轴填空的研究，借助几何画板探索了共直角顶点的两个相似直角三角形的结构及其拓展结论，并在探索过程中分享了一些对几何模型的教学思考．

关键词：几何模型；相似直角三角形；拓展

《义务教育课程标准（2022年版）》将几何直观作为数学课程要培养的学生核心素养“数学眼光”的重要组成部分，在初中数学中，几何直观不再是一种“行为”，而是“意识与习惯”，是核心素养的一种具体表现^［1］．而初中数学的平面几何知识正是将几何直观的培养与具体教学内容建立联系的重要载体．通过图形的运动感受图形之间的关系，从动态的角度理解图形．平面几何是极为重要的构成部分，几何模型是帮助学生进行平面几何学习的有效载体，能促进学生几何学习的高效化．近年来，几何模型及其二级结论在中高考中屡次出现．因此对一些经典的几何模型进行积累和教学是极其重要的．

笔者在七年级期末复习阶段的复习试卷上遇到了一个几何问题，学生的作答情况很不理想，因而通过几何画板进行了相关的研究并记录．

1 引子：遇见好题

1.1 题根

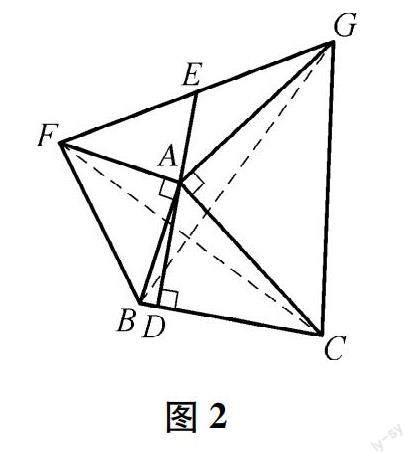
如图1，在△ABC中，AD是BC边上的高，∠FAB=∠GAC=90°，AF=AB，AG=AC，连接FG，交DA的延长线于点E，连接BG，CF（如图2）.则下列结论：① BG=CF；② BG⊥CF；③ ∠EAF=∠ABD；④ EF=EG.其中正确的有_____（填序号）.

简答：结论①②属于“手拉手”模型中的常规题型，由△AFC≌△ABG（SAS）即可证明得到结论①．结论②找“8字模型”即可证得．结论③中∠EAF和∠ABD都是∠BAD的余角，也易得它们相等．结论④简证如下：过F作FN⊥DE，垂足为N，过G作GM⊥DE，交DE的延长线于M（如图3）．在直线DE左侧可证得△FAN≌△ABD（AAS），进而得到FN=AD，同理，在直線DE右侧可证得△AMG≌△CDA（AAS），进而得到GM=AD，因此FN=GM，这为新的三角形全等提供了条件，即可证得△FEN≌△GEM（AAS），从而顺利得到EF=EG，即E为线段FG的中点．故本题正确答案为①②③④．

1.2 学生作答分析

学生对结论①②的掌握还是可以的，但有一部分学生没有选③，当笔者评讲完后学生又觉得十分简单，后悔自己没有看出来，这说明复杂图形让很多学生产生了困扰，学生难以从复杂图形中抽丝剥茧筛选出需要的条件．几乎所有学生对结论④都有疑惑，一些学生通过直尺的测量也得到了正确的结论，不失为解小题目的一种方法．本学期因教学进度紧张，关于全等的知识没有补充详尽，如本题结论④出现的联想构造一线三等角的几何模型，学生对此并不敏感，因此出现了没有找到辅助线导致不会证明的情况，这也在情理之中．笔者在几何画板中通过改变条件对这个问题继续研究，发现本模型中还存在着一些很好的结论．将一个问题扩展到一类问题并把它们研究清楚更有利于我们对问题本质的认识和理解．

1.3 题根的新结论

求证：△FAG的面积和△ABC的面积相等，即S_△FAG=S_△ABC

2 拓展：图形深化

在上面的问题中两个直角三角形是相似的等腰直角三角形，当我们把条件改成相似的非等腰直角三角形，在顺相似和逆相似两种情况下，上述四个结论是否仍然成立？又或者是否有类似的结论成立呢？

4 思考

4.1 几何模型的积累是模式识别的前提

在数学学习中，我们通过对所积累的知识经验进行必要的加工，得出具有长久保存价值的相对固定的题型结构和解题策略，可以成为引领我们进行解题分析的基本模式，当我们遇到一个新问题时，先辨认它属于哪一类基本模式，联想起一个已经解决的问题，检索相应的方法来加以解决^［2］．

模式识别这一解题策略体现了化归思想，有时遵循化陌生为熟悉的情形，有时遵循将问题分解为若干基本问题后再解决的策略．无论是何种策略，模型积累重要性都是显而易见的．我们只有在积累了几何模型之后，才会在遇到新问题时有想法和思路．

4.2 几何模型需要探索精神

我们上面讨论的图形都是共顶点的两个相似的直角三角形的结构，如果我们把直角三角形去掉，换成其他的特殊三角形（如等腰三角形、等边三角形），又会有什么类似的结论呢？这些都是值得思考的．进一步地，如果仅仅是两个相似的普通三角形又如何呢？其实宿迁的这个中考题已经给了我们答案．在数学教学中我们需要这种从特殊到一般的数学思想，去猜想一些结论进而去求证．

众所周知，近年以来，一些情境化的问题考查越来越热门，这些问题往往要求学生在考场上现场读懂题意，学习新知识，进而运用到接下来的问题解决中，探索的意味十分浓厚．在培养学生的探索精神之前，教师应在平时的解题中发挥探索精神，进而将探索精神渗透给学生，逐步培养学生探索的意识并教会他们探索的方式方法．

参考文献：

［1］ 中国教育科学研究院基础教育课程教材研究中心．义务教育课程标准（2022年版）课例式解读［M］．北京：教育科学出版社，2022：63.

［2］ 王怀学.从一种数学模型的探究谈模式识别的“立”与“破”［J］．中学数学月刊，2012（5）：1214.