新型内衬组合波形钢腹板的剪切行为

王晓明 ，张嘉鼎 ，2†，赵建领 ，录哲元 ，汪帆 ，王欢

（1.长安大学 公路学院，陕西 西安 710064；2.中交第二公路工程局有限公司，陕西 西安 710065；3.黄河勘测规划设计研究院有限公司，河南 郑州 450003；4.四川省公路规划勘察设计研究院有限公司，四川 成都 610041）

随着桥梁跨度的增大，大跨度波形钢腹板组合梁桥在支座或墩顶处常承担很大的剪力，进而导致主要承剪的波形钢腹板承担潜在的剪切屈曲风险.此处腹板的抗剪稳定是结构安全的重要控制因素之一.宋建永等［1］的研究表明，增加腹板厚度能显著提高波形钢腹板的剪切屈曲强度，但较厚（大于30 mm）的波形钢腹板的加工变得困难并且不经济.张峰等［2］指出在墩顶或支承处浇筑内衬混凝土能够为腹板提供足够的抗剪稳定性.

尽管在设置内衬混凝土后波形钢腹板结构的弯曲、剪切强度和抗屈曲性能得到增强［3-6］，但同时，墩顶或支承处内衬混凝土约束了波形钢腹板的褶皱效应［7］，明显降低了支承区附近的预应力导入效率.贺君等［8］研究发现，由于内衬混凝土的存在，预应力引起的顶板纵向压应力降低了18%；由于刚度的突然变化，设置内衬混凝土和纯波形钢腹板之间的过渡段具有较大的应力集中，导致该位置处的应力突然变化［9］.

上述问题受到了学者们的广泛关注，对于承担负弯矩的支承区段而言，预应力导入度的下降对顶板抗裂性影响显著.此外，内衬混凝土的存在增大了结构的自重，这与使用钢腹板实现结构轻量化［10-11］的初衷相悖.为了替代混凝土内衬或是减小混凝土内衬的布置长度以实现结构轻量化，并保证墩顶或支承处腹板的抗剪稳定性，已有学者做了宝贵探索，如Wang等［12］和He等［13］及王思豪等［14］提出了一种加劲波形钢腹板，并对其替代混凝土内衬的可行性做了试验和数值研究.

综上，探索提升波形钢腹板剪切稳定性的新措施对于提高组合梁支承区段力学性能具有重要意义.本文提出了一种轻盈的滑槽-栓钉式内衬组合波形钢腹板.通过本构关系、焊接残余应力和几何初始缺陷的敏感性分析建立了数值模拟方案，结合文献［12］中试件W1 的试验数据证明了所采用的模拟方案的合理性，进而研究了新型内衬组合波形钢腹板的轴向刚度和剪切性能.

1 滑槽-栓钉式内衬的构造设计

本文提出了一种采用滑槽-栓钉式连接的新型内衬组合腹板，滑槽-栓钉式连接构造如图1所示.

图1 滑槽-栓钉式连接构造示意图Fig.1 Schematic diagram of chute-stud connection

新型内衬组合腹板的构造如图2 所示，约束立柱与顶底翼缘板焊接，约束立柱与腹板通过滑槽-栓钉连接（滑槽焊接于约束立柱，抗拔不抗剪栓钉焊接于波形钢腹板）.所提出构造的作用机理为：连接构造的抗拔作用使得腹板和约束立柱在面外方向协调变形，因此，具有较大面外刚度的约束立柱能有效限制腹板的面外屈曲变形，从而提高腹板的屈曲强度；由于低弹模发泡材料的存在，可允许滑槽内的栓钉在一定范围内自由滑动，因此不会对腹板的面内变形产生约束，从而使得波形钢腹板的褶皱效应不受影响.

图2 新型内衬组合波形钢腹板工字钢梁构造图（单位：mm）Fig.2 Structure of corrugated web steel I-girder with new encasement（unit：mm）

提出的新型内衬组合腹板结构轻盈，不会显著增加上部结构自重，同时结构的加工焊接可全部在工厂进行，保证精度的同时减少了现场作业量，具备应用前景.

为了研究新型内衬组合波形钢腹板的抗剪性能，结合文献［12］设计了两个工字钢梁试件（分别采用纯波形钢腹板和新型内衬组合波形钢腹板），并通过数值方法进行对比研究.新型内衬组合波形钢腹板工字钢梁的尺寸和构造细节如图2 所示，相应的波形钢腹板工字钢梁除无内衬外，其余尺寸和构造均相同.

2 数值建模方案

2.1 单元类型和边界条件

采用有限元分析软件ANSYS，考虑初始几何缺陷、焊接残余应力和材料非线性的影响，对结构的剪切性能进行了模拟.采用SHELL181 单元模拟波形钢腹板、翼缘板和加劲肋，采用BEAM188 单元模拟约束立柱，抗拔不抗剪栓钉采用COMBINE39单元模拟.

波形钢腹板工字钢梁的力和位移边界条件如图3 所示，试件采用简支，左侧为固定支座（所有节点约束所有平动自由度和转动自由度），右侧为滚动轴承支座［所有节点约束平移自由度（相对于Z、Y轴）和转动自由度（相对于Z、Y轴）］，约束两端加劲肋和跨中上、下翼缘的平移自由度（相对于X轴）模拟侧向支承和侧向位移限制装置.相应的新型内衬组合波形钢腹板工字钢梁的力和位移边界条件均相同.

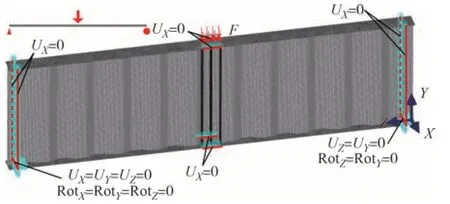
图3 有限元模型Fig.3 Finite element model

2.2 滑槽-栓钉式连接的模拟

为COMBINE39 单元设置合适的本构模型以模拟滑槽-栓钉式连接.焊接在腹板上的抗拔不抗剪栓钉嵌入焊接在立柱上的滑槽将腹板和约束立柱连接，腹板和立柱间的相对变形大致可分为三个阶段：1）外包发泡材料的弹性变形阶段；2）外包发泡材料的塑性变形阶段；3）栓钉变形阶段，即为抗拔不抗剪栓钉的变形过程.因此，腹板和立柱间的滑移关系可用抗拔不抗剪栓钉（URSP）连接器的剪力-滑移关系描述，本文采用Nie 等［15］建议的抗拔不抗剪栓钉（URSP）连接器的剪力-滑移关系（图4）.

图4 URSP剪力-滑移关系Fig.4 The stress-strain relationship of URSP

式中：u0表示外包发泡材料弹性阶段的长度；k00表示弹性阶段的剪切刚度；如式（4）所示，k11和ts满足线性关系，k11表示发泡材料完全压缩后的剪切刚度，ts表示泡沫厚度，Kt是刚度参数，采用了Nie 等［15］建议的值.

2.3 敏感性分析

2.3.1 本构关系

波形钢腹板加工过程中产生的塑性变形无法完全释放，导致材料性能变化，故波形钢腹板的应力-应变关系与平板钢板有所不同，需进行本构敏感性分析以获得合适的应力-应变关系. 分析了4种本构模型（图5）：理想弹塑性模型（EPP）［16］、考虑屈服平台的弹塑性硬化模型（EPYP）［17］、双折线弹塑性模型（EPSH）［18］和Ramburg-Osgood（RO）［19］模型.RO 模型的应力-应变关系为：

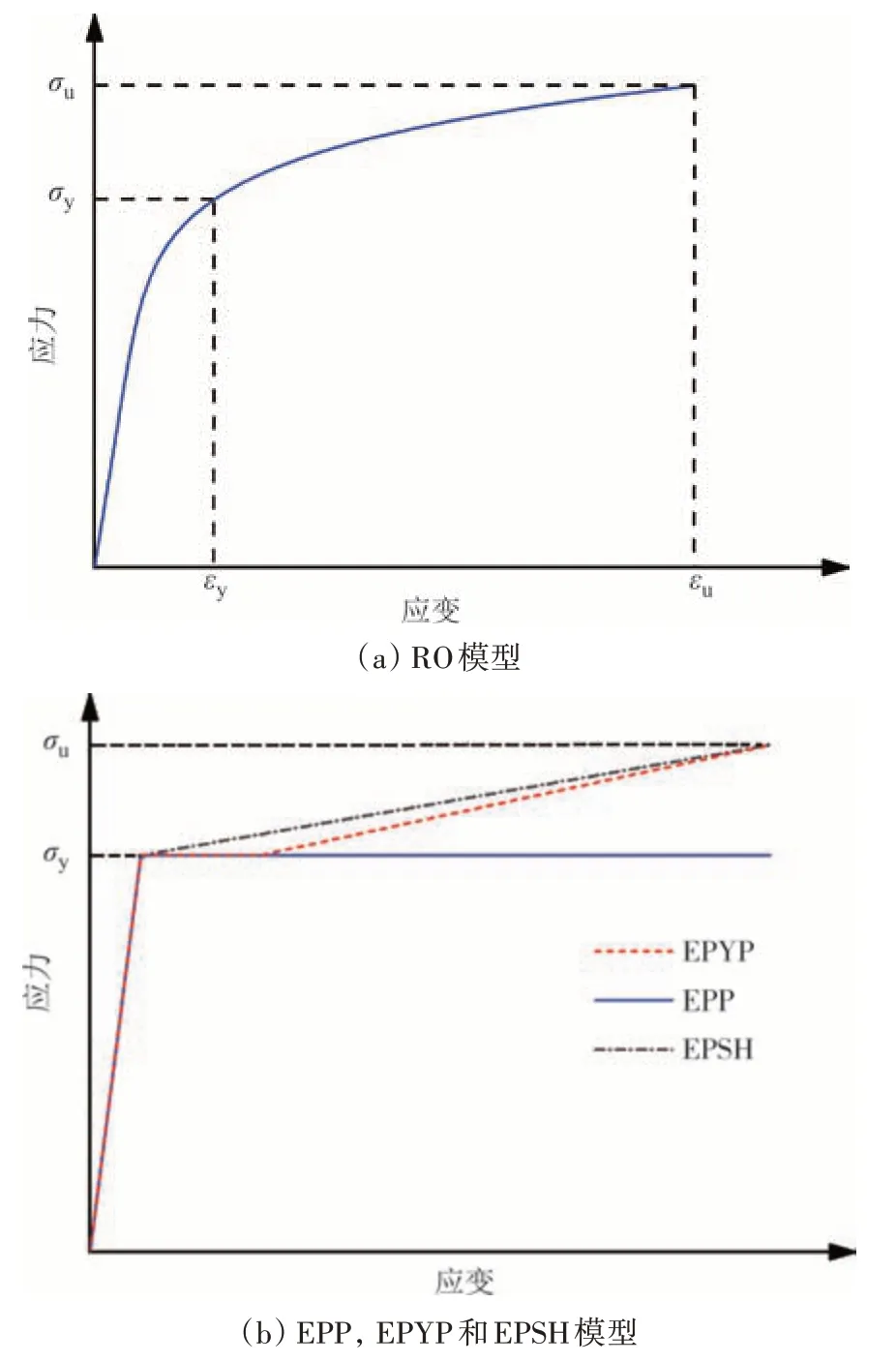
图5 本构关系曲线Fig.5 Constitutive model of stress-strain relationship

式中：σ和ε分别为应力和应变；σp为p%处残余塑性应变对应的应力，对于低碳钢，p=0.2；n为应力-应变曲线的增强系数，对于波形钢板，n=8［19］.加强肋和上下翼缘板采用EPYP 模型模拟.文献［12］中波形钢腹板的杨氏模量E为203 GPa，泊松比μ为0.3，屈服强度fy为400 MPa，极限强度fu为524 MPa.

图6 绘出了采用不同本构模型的荷载-挠度曲线.不同的本构模型对试件的初始刚度没有影响，RO 模型的荷载-挠度曲线比其他三种模型的荷载-挠度曲线表现出更早的非线性行为.EPP、EPSH 和EPYP 模型的承载能力几乎相同，RO 模型模拟的极限承载力小于其他三种模型的极限承载力.不同本构模型之间承载能力的相对误差在10%以内.RO模型与文献［12］试验结果吻合得更好，因此在接下来的有限元分析中波形钢腹板采用RO模型模拟.

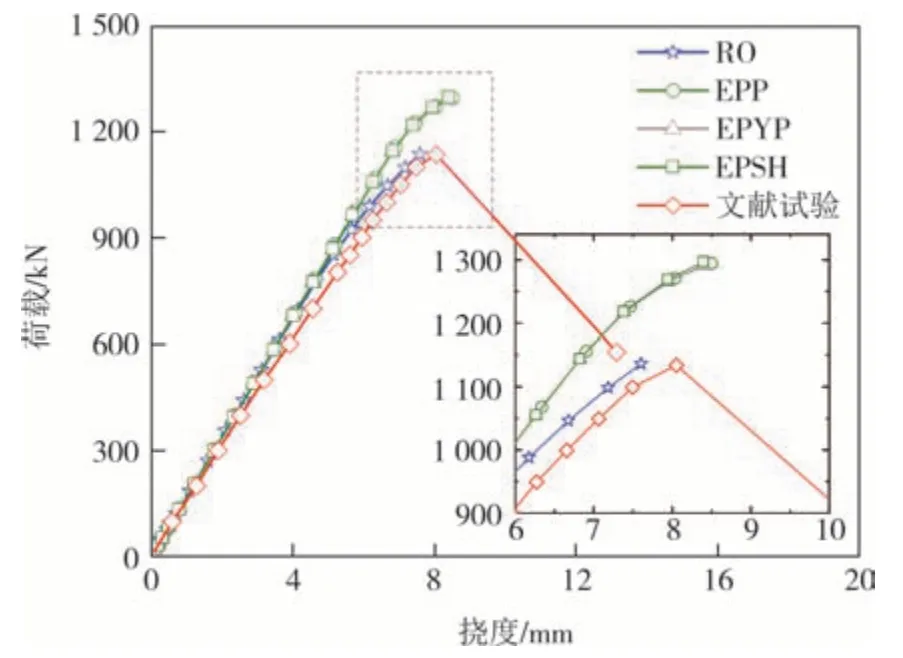
图6 本构关系敏感性分析结果Fig.6 Results of material constitutive sensitivity analysis

2.3.2 焊接残余应力

残余应力对结构力学性能有显著影响.对于波形钢腹板钢梁，残余应力［20］产生的原因有：波形钢腹板和上下翼缘板之间焊缝金属的冷却；由于冷成型而产生的波形弯曲区域；栓钉和腹板之间焊缝金属的冷却.栓钉焊接引起的残余应力仅分布在栓钉附近，其影响可忽略不计.由于屈曲破坏只发生在波形钢腹板上，因此在接下来的分析中不考虑上下翼缘板内的残余应力.

采用He 等［13］使用的残余应力分布模式（图7），与翼缘焊接的波形钢腹板边缘拉伸屈服，并沿腹板高度线性降低至均布抗压强度0.1fy.

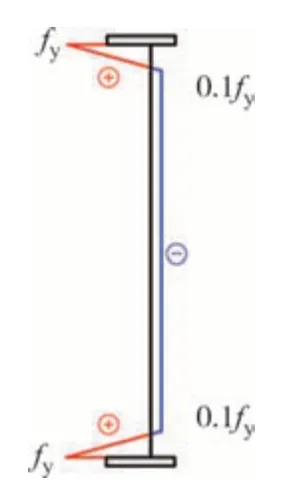
图7 残余应力分布Fig.7 Residual stress distribution

图8 给出了考虑和不考虑残余应力的荷载-挠度曲线，两条曲线的起始段几乎重合，因此考虑或不考虑残余应力不会影响结构的初始刚度，但残余应力的存在会降低波形钢腹板梁的承载力，降低率为4.6%.

图8 残余应力的影响Fig.8 Effect of welding residual stress

2.3.3 几何初始缺陷

Elgaaly 等［21］发现，通过有限元计算的抗剪承载力高于试验测得的抗剪承载力，引入双曲正弦波形式的几何缺陷后，分析结果与试验结果的一致性更好.通常，按拟定幅值缩放的一阶屈曲模式是考虑初始几何缺陷的最佳选择，且计算结果相对保守［21］，本文采用这种方法考虑初始几何缺陷.

对于初始几何缺陷的幅值，EN 1993-1-5［22］建议平腹板梁采用腹板高度的1/200，Jáger等［23］的研究证实了该值适用于波形钢腹板梁.Driver 等［24］认为缺陷幅值应等于腹板厚度.为确定等效几何缺陷幅值，进行了参数分析，图9 为不同初始几何缺陷幅值的荷载-挠度曲线，随着初始几何缺陷幅值变大，试件的初始刚度逐渐降低，但降低幅度不大，表明初始几何缺陷幅值对结构的初始刚度影响很小，但初始几何缺陷幅值的增加会导致结构的承载能力显著降低.当幅值（I/A）从0 增加到2 mm 时，试样的承载力降低了19%.随后，随着幅值的增大，承载能力近似线性下降.可以看出，结构刚度对初始几何缺陷幅值不是很敏感，承载能力对初始几何缺陷幅值敏感.为了使计算结果与文献［12］试验结果一致，等效缺陷幅值取6 mm（腹板高度的1/200）.

图9 初始几何缺陷幅值的影响Fig.9 Effect of initial geometric imperfection amplitude

3 试验验证

3.1 屈曲模态

图10 显示了引入初始几何缺陷、残余应力的FEA 结果和试验结果的屈曲模态对比，可以观察到很好的一致性，均为分布于多个波折范围的交互屈曲，试样屈曲范围相对较小，集中在腹板高度的中部，这与He 等在文献［13］中得到的结果一致.FEA结果与试验结果的差异可能是由初始几何缺陷和残余应力分布不一致导致，FEA 采用了按拟定幅值放缩的一阶屈曲模态作为初始几何缺陷，采用图7 的残余应力分布模式，而实际情况往往更复杂.

图10 屈曲模态对比Fig.10 Comparison of failure modes

3.2 荷载位移曲线

波形钢腹板简支工字钢梁在跨中截面集中荷载P下的跨中挠度（Δ）可计算为Δ=P/k0，其中k0为弹性阶段的初始刚度，同时考虑弯曲刚度kb和剪切刚度ks得出：

式中：E、G分别为弹性模量和剪切模量；I是截面的惯性矩，忽略了腹板因其纵向褶皱效应而产生的贡献，只考虑上、下翼缘；Aw为波形钢腹板的截面积；L为简支梁的跨度；η是波形钢腹板的形状系数，η=（a+b）/（a+c），反映了腹板波形的影响，a和c分别为平行和倾斜子面板的宽度，b为倾斜子面板的投影宽度.

图11 给出了从试验、理论和FEA 三种方法中获得的施加荷载和跨中挠度的关系，三条曲线在起始阶段吻合得很好，说明了有限元模型能很好地反映出结构的初始刚度，FEA 得到的曲线与实测曲线吻合程度较高，表明有限元计算结果较好地预测了结构的承载能力.

图11 荷载-竖向挠度曲线对比Fig.11 Comparison of load-deflection curves

图12 给出了试验和有限元分析得到的外加荷载两个剪切试验区中心点的面外位移的关系，随着荷载增加，有限元与试验获得的挠度都近似线性增长，虽然曲线的近似程度并不理想，但所建立的有限元模型对最终面外位移的大小预测得很好.曲线间的偏差可能同样是由有限元分析采用的初始几何缺陷及残余应力分布和实际情况不一致导致.

图12 荷载-面外位移曲线对比Fig.12 Comparison of load-out of plane displacement curves

3.3 剪切承载能力

表1 给出了试验和有限元得到的极限承载能力和最终挠度的比较.

有限元模型与文献［12］试验得到的极限荷载之比为1.001，误差为0.1%，有限元计算挠度与试验测量挠度之比为0.944，误差为5.5%，表明所建立的有限元模型很好地预测了结构的极限承载力和结构的最终竖向挠曲变形.

3.4 应变分布

图13 显示了在400 kN 的外加荷载下A-A截面的实测正应变和有限元计算正应变分布的比较.从图13 中可以看出应变分布的有限元分析结果与试验结果吻合较好，波形钢腹板的纵向应变相对较小，表明波形钢腹板几乎不提供抗弯承载能力，顶底翼缘板的正应变相对较大，顶底法兰板提供了试件的抗弯承载能力.同时有限元结果与试验结果均能较好地满足拟平截面假定，有限元和试验数据所反映出的中性轴的高度十分接近，均位于腹板高度中心附近.

图13 正应变结果对比Fig.13 Comparison of normal strain

图14 显示了在400 kN 的外加荷载下A-A截面的实测剪应变和有限元计算剪应变分布的比较.从图14 中可以看出剪应变分布的有限元分析结果与试验结果吻合较好，波形钢腹板的剪应变相对较大，表明波形钢腹板提供了结构主要的抗剪承载能力，同时剪应力沿腹板高度均匀分布.

图14 剪应变结果对比Fig.14 Comparison of shear strain

4 新型内衬组合波形钢腹板的纵向刚度和剪切行为

4.1 纵向刚度

为了探究新型内衬对波形钢腹板纵向褶皱效应的影响，比较了纯波形钢腹板工字梁和新型内衬组合波形钢腹板工字梁在相同的位移边界条件和纵向荷载作用下结构的变形值.有限元模型的位移边界条件和加载如图15 所示，左侧节点的6 个自由度均加以约束以模拟固结边界条件，在右侧施加了10 kN轴向荷载，计算结果如表2所示.

表2 纵向刚度对比Tab.2 Comparison of axial stiffness

图15 边界条件Fig.15 Boundary conditions

轴向荷载作用下，结构的纵向变形（Δl）可以计算为Δl=P/ka，ka为结构纵向刚度：

式中：kw为腹板刚度，kf为顶底板刚度；Ef为顶底板弹性模量；Af为顶底板面积；L为结构长度.计算腹板刚度时，需要对波形钢腹板纵向弹性模量E0进行修正，采用有效弹性模量Ew的方式，腹板有效弹性模量Ew的计算原理如下：将波形钢腹板等效为等高度的平面钢腹板，采用两者轴力作用下，纵向变形相同的条件［25］.如图16所示.

图16 波形钢腹板几何参数示意图Fig.16 Schematic diagram of geometric parameters of corrugated steel web

腹板有效弹性模量Ew按式（3）计算：

从表2 的结果可以看出，设置新型内衬前后结构的纵向刚度相差很小，这表明新型内衬并不约束波形钢腹板的纵向变形，不影响波形钢腹板纵向褶皱效应.

4.2 应变分布

图17 显示了在400 kN 的外加荷载下，新型内衬组合波形钢腹板和纯波形钢腹板结构A-A截面的剪应变分布情况的有限元计算结果.可以看出两个结构的应变分布十分接近，且都呈现出相同的规律：波形钢腹板的剪应变相对较大，顶底翼缘板的剪应变相对较小.表明波形钢腹板提供了结构主要的抗剪承载能力，而顶底法兰板承担的剪力相对较小.

图17 剪应变分布Fig.17 Distribution of shear strain

图18 显示了在400 kN 的外加荷载下，新型内衬组合波形钢腹板和纯波形钢腹板结构A-A截面的正应变分布情况的有限元计算结果.可以看出两个结构的应变分布十分接近，且都呈现出相同的规律：波形钢腹板的正应变相对较小，顶底翼缘板及其附近腹板的正应变相对较大.表明波形钢腹板几乎不抵抗弯矩，顶底翼缘板提供了试件的抗弯承载能力，在栓钉附近位置并未出现正应变突变，表明内衬的设置不影响波形钢腹板的纵向刚度.两者均能较好地满足拟平截面假定，中性轴的高度均位于腹板高度中心附近.

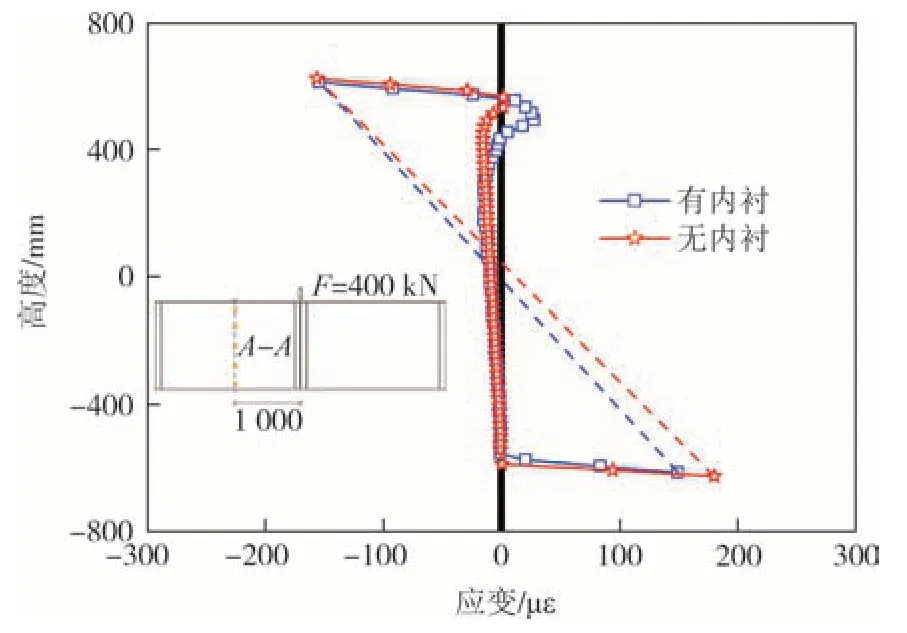
图18 正应变分布Fig.18 Distribution of normal strain

4.3 屈曲模态

图19 展示了跨中加载时，引入初始几何缺陷后新型内衬组合腹板的屈曲模态，可以看到新型内衬组合腹板的屈曲模式与纯腹板的屈曲模式一致，均属于跨越多个波形的交互屈曲模式，屈曲高度集中在腹板高度中部.

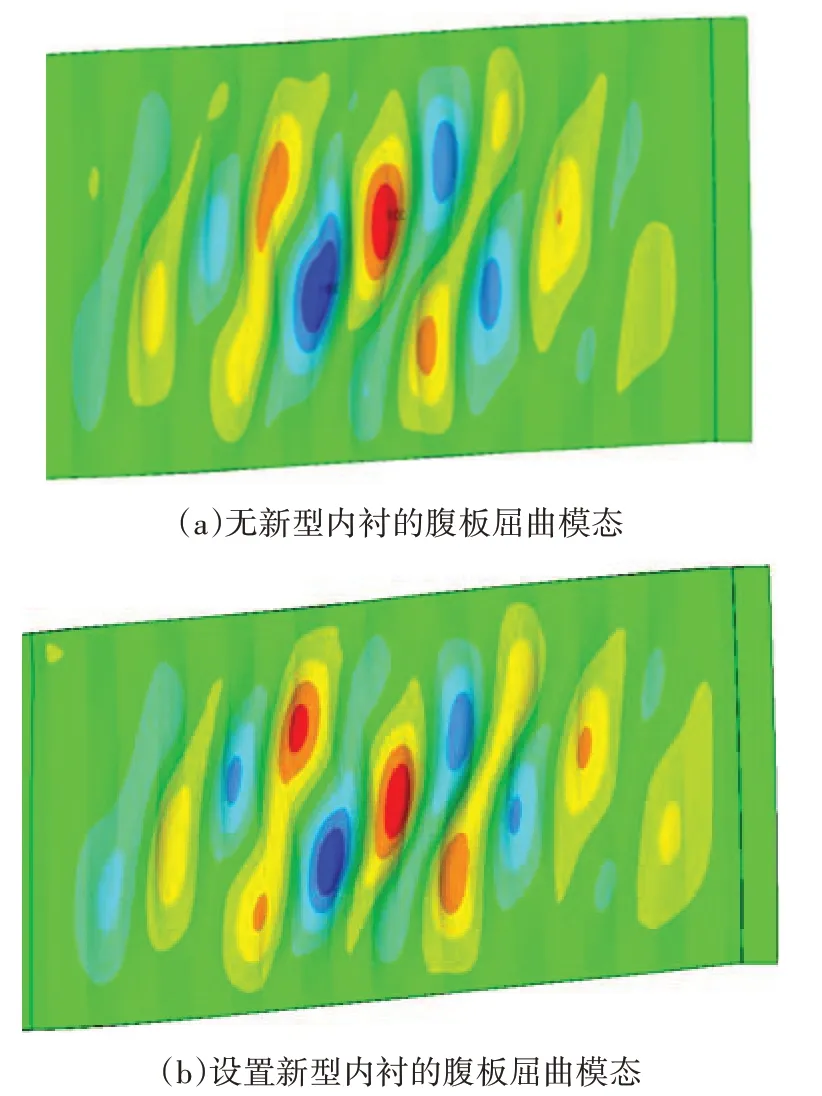
图19 屈曲模态Fig.19 Buckling mode

4.4 荷载位移曲线

分别从理论和有限元分析两种方法中获得了带有新型内衬的波形钢腹板梁的跨中施加荷载和跨中挠度关系，如图20 所示.图20 中两条曲线在起始阶段吻合得很好，有限元分析结果和理论结果吻合程度较高，随着荷载增大到约900 kN，荷载位移曲线开始表现出了明显的非线性，这表明结构已加载至非线性受力阶段，这与纯波形钢腹板模拟得到的进入非线性阶段的荷载水平相近，但带有新型内衬的波形钢腹板梁的剪切承载能力更高，约为1 400 kN，增幅约为23%，破坏时跨中的竖向挠度达到了约13 mm，增幅约71%，在承载力提高的同时结构整体的延性也有所提高.

图20 荷载-挠度曲线Fig.20 Load-displacement curves

图21 给出了带有新型内衬波形钢腹板两个剪切试验区中心点B2、B3的荷载与侧向位移的关系曲线.在加载早期，B2 与B3 两个位置处的面外位移几乎随外加荷载的增加而线性增加，但变形增加较为缓慢.在加载至约1 000 kN 时，面外变形迅速开展，荷载与侧向位移的关系曲线显示出了明显的非线性特征.同无内衬结构的面外位移荷载曲线对比可以看出，在加载初期，新型内衬为腹板提供了有效的面外约束，提升了腹板的初始面外刚度，约束了早期面外位移的开展速度；在加载后期，新型内衬的存在限制了面外位移的开展程度，推迟了腹板屈曲的发生，从而提升了结构的承载能力.

图21 荷载-面外位移曲线Fig.21 Load-out of plane displacement curves

5 结论

针对传统混凝土内衬约束波形钢腹板褶皱效应的问题，提出了一种滑槽-栓钉式连接的新型内衬，并进行了数值研究，分析了新型内衬对波形钢腹板褶皱效应和抗剪性能的影响，得出如下结论：

1）通过既有试验数据验证，说明所采用的数值模拟方案能有效模拟结构的剪切行为，包括剪切屈曲模态、剪切强度和刚度.

2）设置新型内衬前后，结构的纵向刚度几乎不变，表明新型内衬并不约束波形钢腹板的纵向变形，对波形钢腹板的纵向褶皱效应影响很小.

3）设置新型内衬后，剪应变仍沿腹板高度均匀分布且正应变仍服从拟平截面假定.

4）设置新型内衬后，结构的极限承载能力和破坏时的延性均有提升，同时设置新型内衬前后结构剪切屈曲模态并未改变，均为交互屈曲.其中，结构的极限承载能力提高约23%，破坏时的竖向挠度增大约71%.

5）新型内衬为腹板提供了有效的面外约束，提升了腹板的面外刚度，约束了早期面外位移的开展速度；在加载后期，新型内衬的存在限制了面外位移的开展程度，推迟了腹板屈曲的发生.