基于无人机航拍的近地风场类别确定方法
李正农 ,代向奎,蒲鸥,吴红华
[建筑安全与节能教育部重点实验室(湖南大学),湖南 长沙 410082]
目前,在进行结构抗风设计时,为了确定风荷载,首先要确定其风场类别,传统的风场类别确定方法主要依据《建筑结构荷载规范》(GB 50009—2012)[1]规定的四类地貌.但李正农等[2]研究发现,高层建筑受到的风荷载是受周边环境影响的,该规范中不同地貌的风场类别判定无法完全涵盖一个地区的所有位置,因此,对于城市地区,这种分类方法较为粗糙且界定标准不够细化.空中风场受地貌影响会随高度呈现一定的变化规律,我国通常采用指数律来拟合风速剖面并确定其风场类别,常用的测量方法包括测风塔[3]、风廓线雷达[4]和移动激光雷达[5]等.测风塔安装难度大、易受场地限制,在城市地区进行多点测量时难度很大[6];移动雷达空间分辨率较低且价格昂贵[7].因此城市风场难以采用传统方法进行测量.吴红华等[8]和李正农等[9-10]提出了采用两台搭载风速仪的无人机同步测量的方法进行近地风场的测量并识别其风场类别,该方法具有较高的空间灵活性且成本较低,但由于一些风向很少出现,无法长期进行现场实测,该方法无法判定所有方向的风场类别.
鉴于通过空中风场测量确定风场类别的局限性,地貌识别或将成为更加精确且应用广泛的确定风场类别的新方法.识别地面地貌状况的方法大致分为两种,第一种是通过空中风场测量,根据其变化规律来进行地貌状况的判断,第二种是根据实际地面粗糙度进行地貌状况的判断.在地面粗糙度识别方面,张相庭[11-12]利用风耗散能原理对各地貌进行分析,并通过建立α值与风耗散能η的关系实现了按照实际地貌计算地面粗糙度指数α值,但随着大量新建建筑的出现,该方法的精确度及适用性都大大降低.Alam 等[13]利用卫星遥感分析技术对卫星图像进行波段处理,根据其反射率确定土地覆盖类型,然后结合空间算法形成粗糙度等级图,实现了无须现场测量的地面粗糙度分类方法,但该方法只进行了几千平方千米区域的分类测试,在城市局部区域中的分类精确度并未进行研究.城市地区地面粗糙度主要由建筑物形成,研究者们根据建筑物高度和建筑物密度等因素提出了地面粗糙度的计算公式[14-16],但城市地区建筑物众多,粗糙度识别较为复杂.近年来通过无人机影像进行地面建筑物信息识别的技术得到广泛应用,Vacca 等[17]和Koc 等[18]对基于无人机航拍得到的建筑物精度进行了研究,结果表明通过设置合适的航拍参数可以获得较高精度的建筑物尺寸信息;Subrahmanya 等[19]根据无人机图像结合人工神经网络算法提供了准确的建筑物识别信息;董彪等[20]和Gao 等[21]均基于Yolov3 算法进行改进,在遥感图像的建筑物检测中展现出了较高的检测精度.基于无人机航拍可以获取城市地区地面建筑物信息,但现阶段尚未建立有效的依据实际地貌状况进行城市地区风场类别识别的方法.
本文应用无人机航拍城市地区地面照片,结合图像识别技术获取建筑物信息并对地貌状况进行分析,通过计算出地面粗糙度Z0并利用风剖面对比获得与Z0对应的粗糙度指数α,进而建立一种应用无人机航拍地貌状况获取测区地面粗糙度指数α并判定其风场类别的方法.本文所提出的方法具有较强的普适性,实现了依据实际地貌判定城市地区风场类别,其结论可为城市地区建筑抗风设计提供参考.
1 实测概况
1.1 实测设备
如图1(a)所示,利用两台搭载风速仪的六旋翼无人机进行来流风场的实测,一台无人机悬停在100 m 高度处作为参考,另一台无人机在10~120 m高度范围内进行测量,本文采用10 个高度进行风剖面计算.风速仪安装在无人机机身上部20.20 cm 处(0.53 倍旋翼直径)以减小机翼转动产生的不利影响.经改装后风速仪由无人机直接供电并将所测数据通过与其相连接的无线电台实时传输到计算机端.本次实测前已在风洞实验室对风速仪进行标定并进行误差修正,通过该方式测量风场的可行性已由Li等[22]进行了试验验证.

图1 实测所用系统Fig.1 System used in the measurement
如图1(b)所示,采用P4 multispectral无人机对测区内各建筑物进行拍摄,本文分别在100 m 和120 m高度处对各建筑物依次进行正射航拍,航拍均选择在光照条件较好时进行以避免因照片清晰度不足而影响建筑物信息提取,通过对照片的识别获得各建筑物尺寸信息,进而获取测区内的地貌状况.
1.2 场地概况
本试验选定两处场地分别进行风场实测和地面粗糙度计算,如图2 所示,实测场地均为建筑物较为密集的城市地区.测区一中以五角星标为目标区域判断来流方向(箭头所示)的地貌类别,该测区来流方向有较多形状规则且相似的建筑物.测区二中以圆标为目标区域判断来流方向(箭头所示)的地貌类别,测区二来流方向有较多的均匀小区和工厂,部分建筑物由于地图未及时更新,因此在图2(b)中未显示.按照《建筑结构荷载规范》(GB 50009—2012)[1](以下简称规范)中关于地面粗糙度的分类标准可将两处测区大致判断为C 类地貌,地面粗糙度指数为0.22左右.
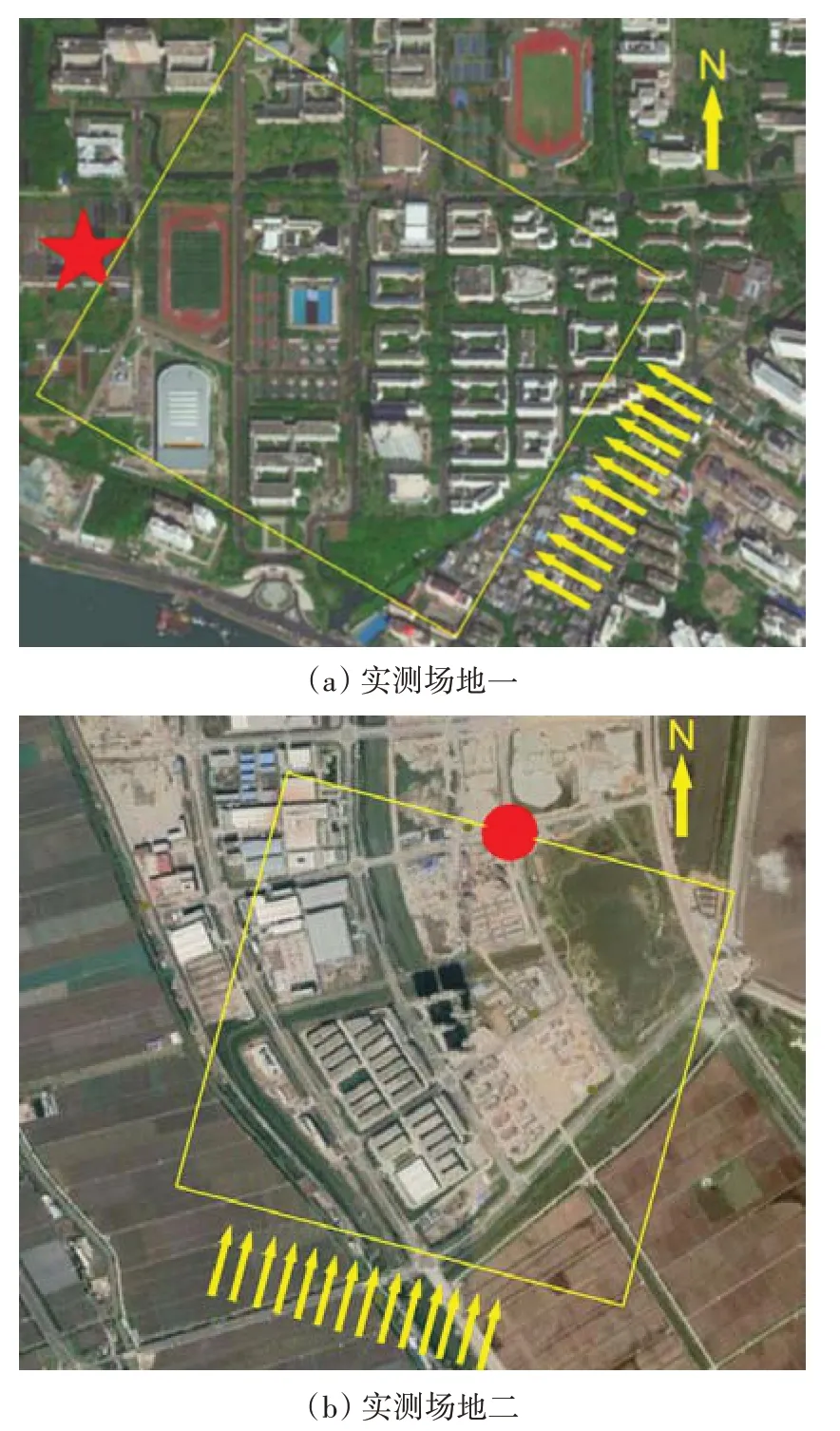
图2 实测场地Fig.2 Test site
实测期间风场条件比较理想,选取风速较大且风向稳定(变化幅度集中在7°以内)的时段进行来流方向风场测量.在地面粗糙度计算过程中仅考虑建筑物为主要粗糙元,并且考虑到较远处建筑物对目标建筑的影响较小,对测区一来流方向约800 m 范围内、测区二来流方向约1 000 m 范围内的建筑物进行了拍摄及计算,具体范围如图2所示.
2 实测数据前处理与风场类别的判定
2.1 实测数据前处理
在实际测量过程中,由于无人机自身的抖动以及机身倾斜等因素会对所采集的风场数据有一定的影响,结合风速仪在风洞实验室中的标定结果,按照公式(1)对无人机所采集的数据进行修正,不同风速区间的修正系数见表1.
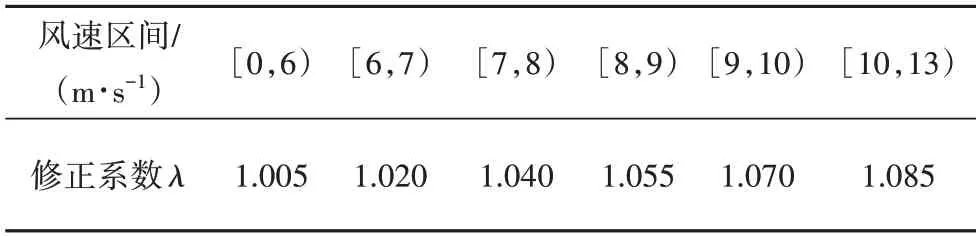
表1 无人机机身修正系数Tab.1 UVA fuselage correction coefficient
式中:u(t)为修正后的无人机风速时程数据;uw(t)为无人机原始风速时程数据;λ为修正系数.
2.1.1 平均风速和平均风向角
现场实测风速仪直接采集的原始数据为风速、风向时程,按照公式(2)进行分解可得到x、y方向的风速分量(图3),各工况下的平均风速U和平均风向角φ根据公式(3)~公式(6)计算.
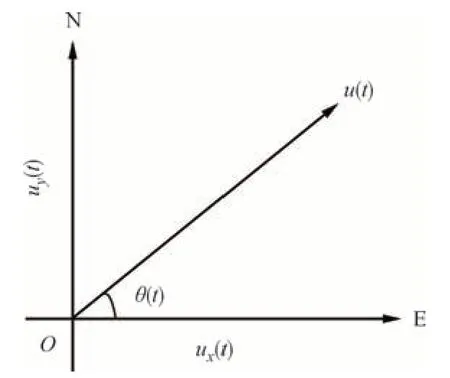
图3 风速时程分解示意图Fig.3 Wind speed time-history decomposition
式中:ux(t)为E 方向分解风速时程;uy(t)为N 方向分解风速时程;u(t)为风速时程;θ(t)为风向时程.
式中:n为测量时距内的采集数目为x方向分解风速平均值为y方向分解风速平均值;U、φ分别为各工况下测量时距内的平均风速和平均风向角.
2.1.2 地面粗糙度指数α1实测原理
由于地表粗糙程度的影响,在大气边界层内风速随高度发生变化,根据规范有关内容可按照指数律[公式(7)]进行风剖面拟合.本试验采用两台搭载风速仪的六旋翼无人机同步测量,无人机B 分别测量10~120 m 范围内不同高度处的风速,无人机A 悬停在100 m 高度作为参考并获得与无人机B 对应的10 个样本数据,用参考文献[10]的方法对无人机所测风场数据进行归一化,并采用公式(8)拟合得到地面粗糙度指数α1.
式中:Z为离地高度;UZ为Z高度处的风速;U10为参考高度10 m 处的风速;UA-i和UB-i分别为机身修正后无人机A和无人机B在各工况下测量的平均风速,i=1,2,…,10;ZB-i为无人机B 在各工况下的对应高度;ZA为无人机A悬停参考高度,本文为100 m.
2.1.3 湍流度
湍流度是反映脉动风速相对强度的一种度量指标,通常采用平均时距内脉动风速均方根与平均风速的比值来表示,即:
在我国规范中,湍流度沿高度的分布按照公式(11)进行计算:
式中:I10为10 m 参考高度处的名义湍流度,对应于A、B、C 和D 类地面粗糙度,可分别取0.12、0.14、0.23、0.39.
2.2 无人机航拍识别地面粗糙度
本研究以城市区域建筑物作为主要粗糙元进行地面粗糙度的计算,由于建筑物成像大小受航拍高度影响,本文采用两个高度分别进行拍摄以实现建筑物尺寸的计算,其中航拍高度计算方法[23]如式(12):
式中:H为航拍高度,m;f为镜头焦距,mm;GSD为地面采样距离,cm/pixel,其实质为用地面距离单位表示像素大小;a为像元尺寸,即图像中单位像素点的尺寸(影像传感器宽度/图像宽度).
2.2.1 相机标定
摄影成像的过程是将三维地物投影到二维平面上,即坐标转换的过程,相机标定主要有两个作用,一个是根据坐标转换过程计算出相机的内、外参数[如公式(13)],另一个是获取镜头畸变参数进行图像校正.理想情况下由三维物理坐标系中一点(Xw,Yw,Zw)到二维像素坐标系中(m,n)的转换公式如式(13):
式中:Zc为物体与光心之间的距离;fx=f/dx,fy=f/dy,f为焦距;(m0,n0)为图像的中心位置,该矩阵为相机的内参矩阵;R为3×3的旋转矩阵,T为3×1的平移向量,该矩阵为相机的外参矩阵.
在实际成像过程中机身姿态、光学透镜固有的透视失真等因素会导致相机成像产生一定程度的变形,本文按照Zhang[24]标定方法采用Matlab对无人机相机进行标定.如图4(a)所示,对标准7 行9 列形式的25 mm×25 mm正方形网格标定板进行不同位姿的拍摄(本文采用20 张照片进行标定),根据各网格角点的空间坐标和对应的像点坐标之间的变换关系进行相机内参、外参及畸变参数的计算.图4(b)给出了相机标定的重投影误差(各网格角点的实际投影像点与根据相机标定结果计算出的理论投影像点之间的距离)直方图,通常认为误差在0.3 以内即满足精度要求,本次标定结果的平均误差为0.14 Pixel 且最大误差为0.16 Pixel,因此本次标定结果有效.
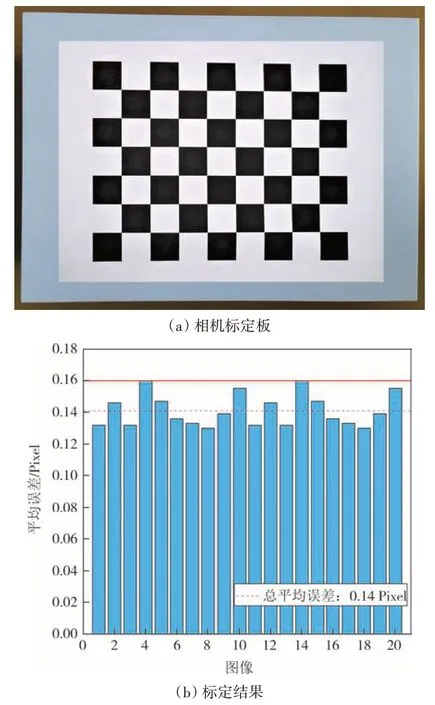
图4 相机标定Fig.4 Camera calibration
通常将镜头畸变分为径向畸变和切向畸变,径向畸变是成像过程中的主要畸变,它是以畸变中心为中心点,沿着镜头半径方向产生的位置偏差;切向畸变是安装过程中镜头本身与图像平面不平行而产生的误差.消除畸变误差的计算公式如式(14):
式中:m、n为原始图像上的坐标位置;x、y为校正后的坐标位置;r为点到成像中心的距离;k1、k2、p1、p2和k3为5个畸变参数,通过相机标定得到.
2.2.2 建筑物识别定位
城市地区建筑物众多且特征较为复杂,传统的目标检测方法无法满足工程应用需求,本文采用基于端到端的Yolo 算法[25]进行建筑物检测.Yolo 系列算法在不断改进与发展[26-27],Yolov5 是目前较为成熟的识别算法,其通过回归能够快速检测出图像中物体的类别和边界框坐标,在检测速度和精度方面均有很好的效果且在工业领域被广泛使用.
Yolov5的网络结构分为Input、Backbone、Neck和Head 四部分,相较于之前的版本进行了一定的优化:在输入端采用Mosaic 数据增强等方式来提高小目标的检测效果;在Backbone 阶段引入Focus 结构和CSP 结构提高网络的学习能力;在Neck 阶段引入FPN 和PAN 结构来增强网络特征融合的能力;在输出端采用CIOU loss 作为预测框的损失函数.在检测过程中Yolov5将输入图片划分成三种不同尺度的网格,当物体中心点落在网格内部时,由该网格负责预测该物体,每个网格都会预测出3 个边界框和其所包含物体的类别概率,每个边界框都包含其坐标信息和置信度.置信度是边界框包含物体的概率与边界框定位准确性的乘积[如公式(16)],将边界框的置信度与其所属网格预测出的类别概率相乘可得到该边界框包含某类物体的概率,通过阈值过滤和非极大值抑制筛选出置信度评分最高的边界框作为输出结果.
式中:c为边界框的置信度;Pr(Object)代表边框包含物体的概率;P表示预测边界框;G 表示人工标注框;IOU越接近于1代表定位越准确.
预测框输出结果为预测物体的置信度以及预测框的坐标,根据预测框对真实框的预测误差构造损失函数,并通过梯度下降的方式不断优化获得网络结构在各阶段的最优权重参数.Yolov5 算法的损失函数包含预测框定位损失、置信度损失和分类损失三部分,其中置信度损失和分类损失与之前版本一致都采用交叉熵损失[26],预测框定位损失采用CIOU loss[公式(18)],综合考虑了预测框和标注框的重叠面积、中心点距离和长宽比等因素.
式中:Lobj为Yolov5 算法损失函数;Lbox为预测框定位损失;Lconf为置信度损失;Lclass为分类损失;λ1、λ2和λ3为权重系数.
式中:b、h和w分别为预测框的中心点位置、高度和宽度;上标gt(ground truth)表示人工标注框;IOU 为预测框和标注框的交互比;ρ为预测框和标注框的中心点距离;d为预测框和标注框的最小外接框的对角线长度;s为预测框和标注框的宽高比的相似度.
本文采用Yolov5 算法识别图像中建筑物,从TorontoCity 数据集和中国典型城市建筑物实例数据集[28]以及本研究在多个城市区域所拍摄照片中挑选出2 000 张图像,共包含建筑物近10 000 座,并使用Labelimg 标注工具对图像中建筑物的矩形边界进行标注(图5),制作本文所需的数据集.为得到适合建筑物检测的先验框维度,在训练之前使用k-means算法对标注框进行聚类分析,本文得到的先验框尺寸为59×42、45×84、116×80、89×165、173×113、152×260、257×176、412×268 和269×440,并将数据集中的图像按照7∶2∶1 的比例分别作为训练集、测试集和验证集.本文训练过程中初始学习率设置为0.001,采用Adam 优化器,动量为0.937,置信度阈值为0.5.图6 给出了本文模型训练阶段的损失图,可看出该模型表现出较好的收敛性,训练迭代次数为300 时最终损失值稳定在0.13 左右,此时平均准确率MAP达到80%.

图5 标注界面Fig.5 Dimension interface
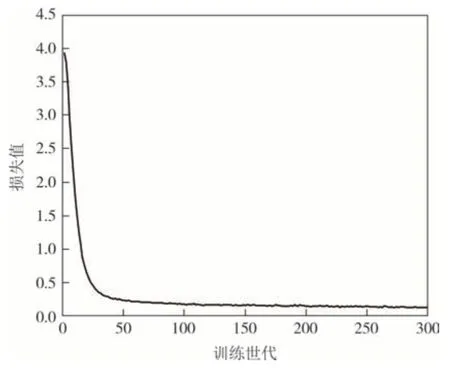
图6 损失函数曲线Fig.6 Loss function curve
根据训练得到的权重参数对校正后的图像进行预测,预测框的输出信息包括物体类别、置信度和预测框定位参数(中心点坐标、宽度和高度),其中一组输出结果如图7所示.

图7 建筑物识别Fig.7 Building identification
2.2.3 建筑物尺寸计算
本文采用两个高度分别对建筑物进行拍摄,图8给出了无人机航拍获得建筑物正射影像的示意图,建筑顶面垂直于光轴且与像平面平行,以2.2.2 节中输出的矩形预测框作为建筑物的平面边界,由于建筑物大多为规则体且顶面为矩形,故以长方体作为建筑物的外边界进行尺寸计算.图8 中根据同一建筑物在两个高度所拍摄照片中得到的建筑物定位框与建筑物实际边界尺寸之间的几何相似关系可得到各建筑物的尺寸信息,具体计算公式如式(19):
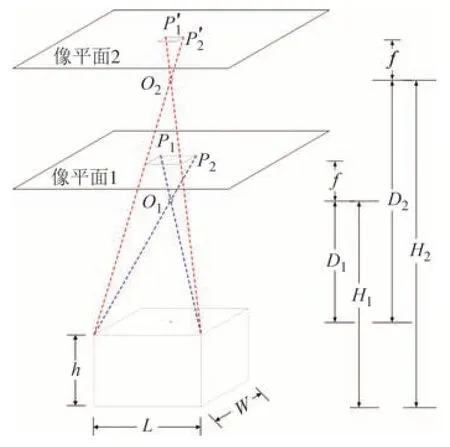
图8 建筑物测量Fig.8 Building measurement
式(19)中及图8中,h、L和W分别为建筑物的实际高度、长度和宽度;P1、P2和P′1、P′2分别为像平面1、像平面2 中建筑物定位框的长度和宽度,单位为pixel;D1、D2分别为像平面1 和像平面2 与建筑物顶面之间的距离;O1、O2分别为两个高度处的镜头中心;a为像元大小,本文中为 3 μm×3 μm;f为焦距,根据2.2.1节标定结果为5.83 mm;H1和H2为无人机离地高度,本文采用100 m和120 m.
经验证本文得到的建筑物尺寸误差控制在5%以内,可满足本研究所需精度要求.本文中建筑物识别及尺寸计算具体流程如图9所示.
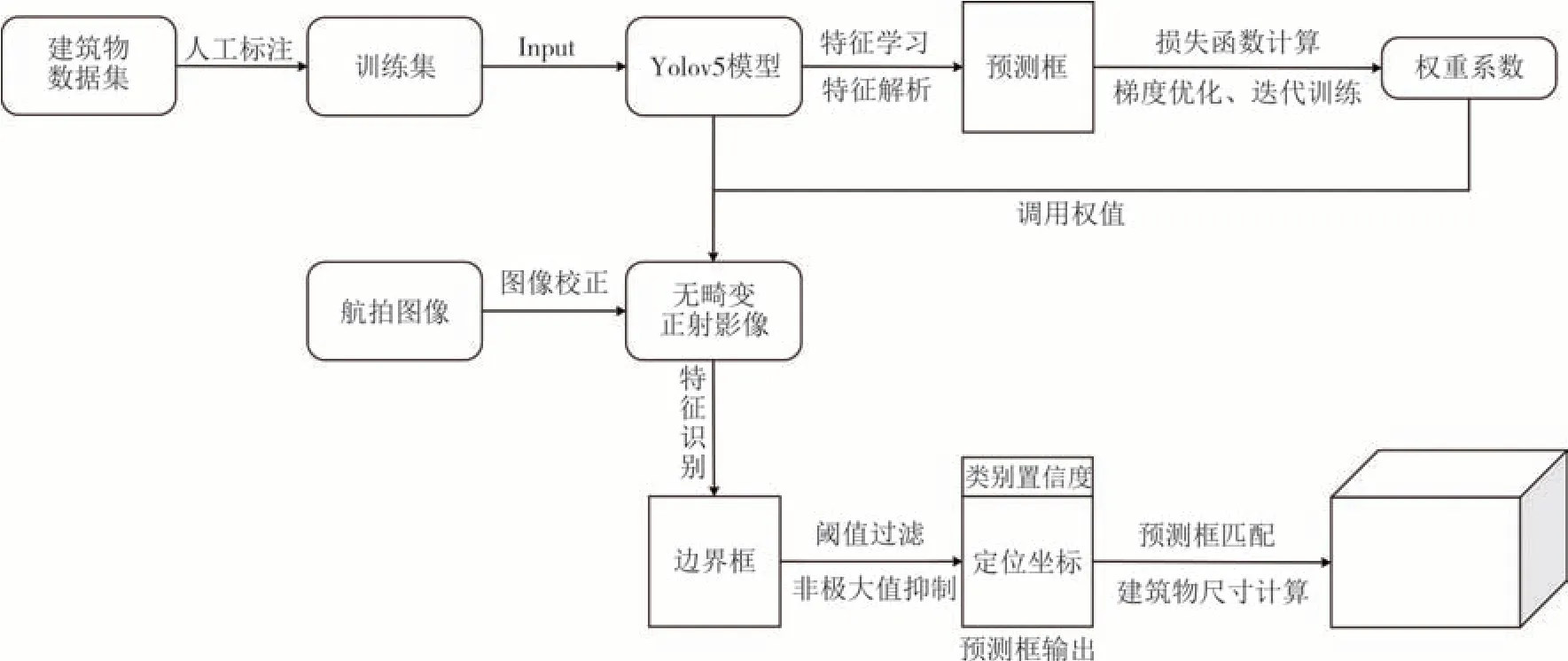
图9 建筑物识别流程Fig.9 Building recognition process
2.2.4 地面粗糙度Z0
对数律风剖面公式中,平均风速U可表示为地面以上高度Z的函数,若已知ZS高度处风速值US,其一般表达式[29]为:
式中:U为Z高度处的风速(Z为离地高度,本文仅对20 m 以上进行分析);Z0为风速等于0 的高度,随地面粗糙程度而变化,称为地面粗糙度.
关于地面粗糙度Z0因对粗糙元的考虑因素不同而有不同的估算方法[30],在本文中只考虑建筑物为粗糙元,主要影响因素为来流方向建筑物的高度、密度等,并且考虑到各个粗糙元的变化,本文采用Kondo等[15]给出的方法进行Z0的计算:
式中:Si代表粗糙元i占有的实际水平面积;hi代表该粗糙元的高度;S为计算范围内的总面积.
3 风场实测数据及地貌状况的分析
3.1 测区一分析
3.1.1 风场实测α1
本次试验采用两台搭载风速仪的无人机进行来流风场测量,无人机A 悬停在100 m 高度处作为参考,无人机B 在10~120 m 范围内依次测量10 个高度处的风速,测量过程中各工况下两风速仪所采集风向角误差均在3°以内,故可直接进行比较.无人机所测风场数据经机身校正、归一化处理后按照公式(8)和公式(11)分别进行风剖面和湍流度剖面拟合,结果如图10所示.
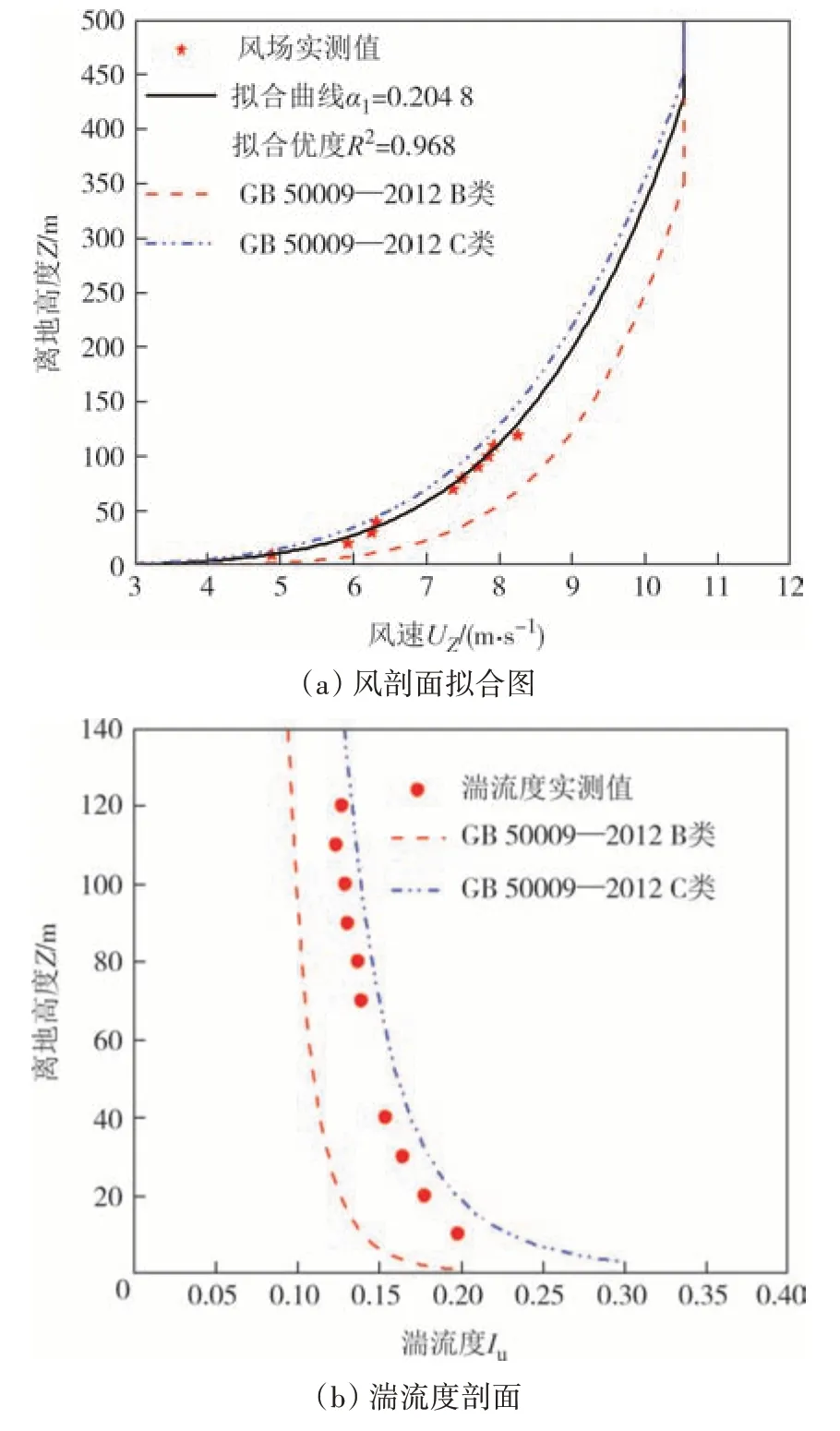
图10 测区一风场拟合Fig.10 Fitting of wind field in test site 1
由图10(a)可知,测区一中由风剖面拟合所的实测地面粗糙度指数α1为0.204 8,拟合优度R2为0.968,拟合曲线介于B、C类地貌之间且与C类地貌吻合程度更好.图10(b)给出了测区一的实测湍流度数据及规范中B类、C类地貌的湍流度剖面,可知实测湍流度与规范中C类地貌更贴近,同风剖面拟合结果较一致.
3.1.2 地面粗糙度Z0计算
测区一总面积为S1=520 104.152 6 m2,所选范围内共计38 处建筑物,根据2.2 节中方法识别图像中的建筑物,对各建筑物进行信息提取如图11 所示.根据公式(21)计算可得测区一的平均地面粗糙度为:
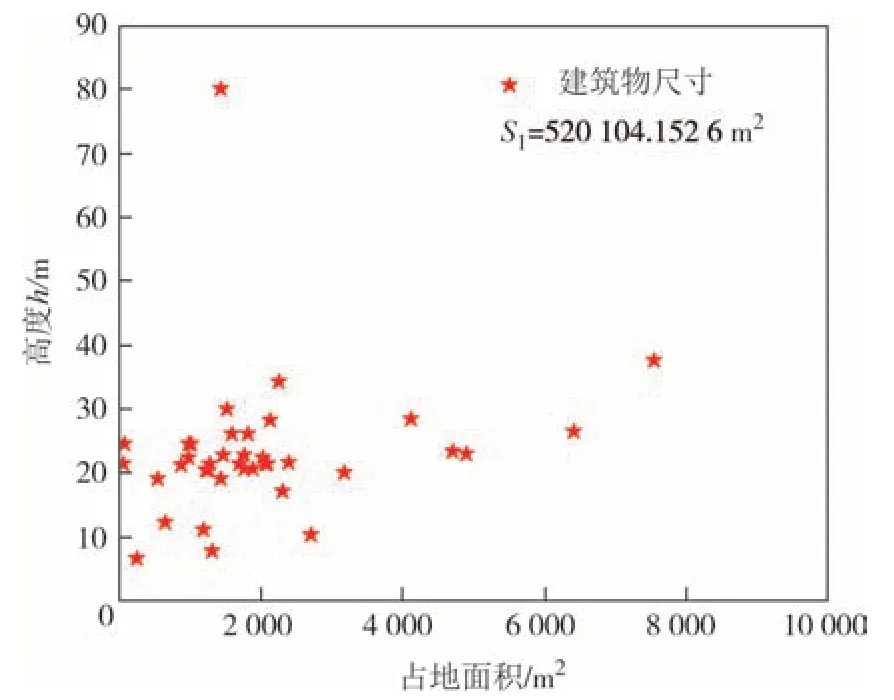
图11 测区一建筑物信息Fig.11 Building information in test site 1
3.1.3 由地面粗糙度Z0计算所得α2
在各种地貌的梯度风高度以上区域,风的流动已不受地面粗糙度的影响,各处风速均属相同,均为梯度风速[29].在同一梯度风速下分别按照公式(7)和公式(20)绘制风剖面,并采用欧式距离公式[31]判断出吻合程度最高的α2值.具体计算公式如下式(22)~(24):
式中:v0为测区一所在地区的基本风速;vG为测区一所在地区的梯度风速值;U1、U2分别为根据指数律和对数律得到的不同高度处风速值;ZG为规范中定义的与α2相对应的梯度风高度,并根据不同的α2值按比例确定;d为欧式距离指标.
根据规范[1]中《全国基本风压标准值表》查得测区一基本风压为0.75 kN/m2,计算可知该地区基本风速为v0=34.64 m/s(考虑到城市地区下垫面粗糙度较大,一定高度以下风速随高度的变化比较紊乱,不一定符合对数规律或指数规律[32],故本文从20 m 高度处开始,并以200 m 高度范围为例进行计算).图12为α2在0.150~0.250(精确度为0.001)范围内对应的d值变化曲线,对应于α2=0.198 时d取得最小值.图13为d取得最小值时两指标对应的风剖面对比图.
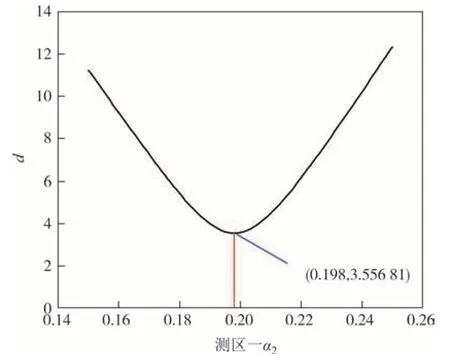
图12 测区一d值变化曲线Fig.12 Change curve of d value in test site 1
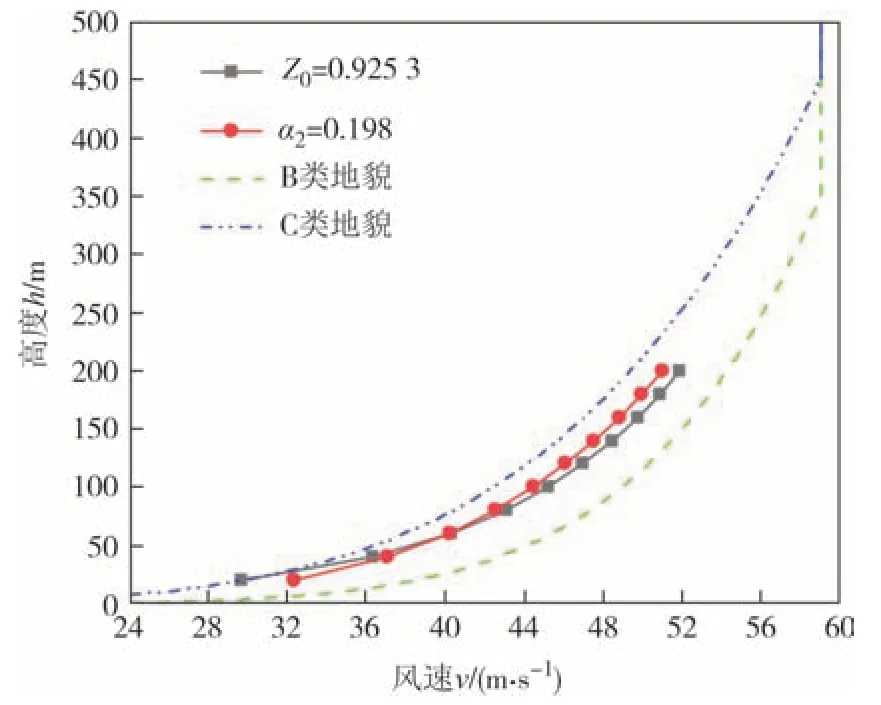
图13 测区一风剖面对比图Fig.13 Comparison of wind profiles in test site 1
3.1.4 误差分析
根据地面粗糙度计算所得α2值与风场实测所得α1值比较接近,图14 给出了两种方法在同一梯度风速的风剖面误差图(近地面200 m 范围内).由图14可知,这两种方法得到的风剖面曲线较为贴近,相对误差为3.32%.分析可知测区一的风场类别介于B、C类之间,考虑到城市地区个别建筑物高度超过200 m,分别对近地面350 m(B类地貌梯度高度)和450 m(C 类地貌梯度高度)高度范围进行计算及误差分析,结果如表2所示.
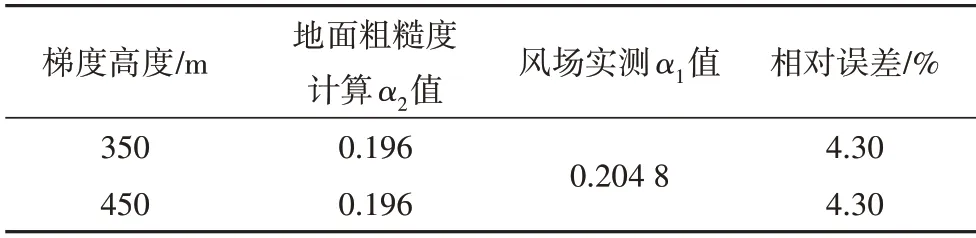
表2 测区一不同高度误差分析表Tab.2 Error analysis of different heights in test site 1
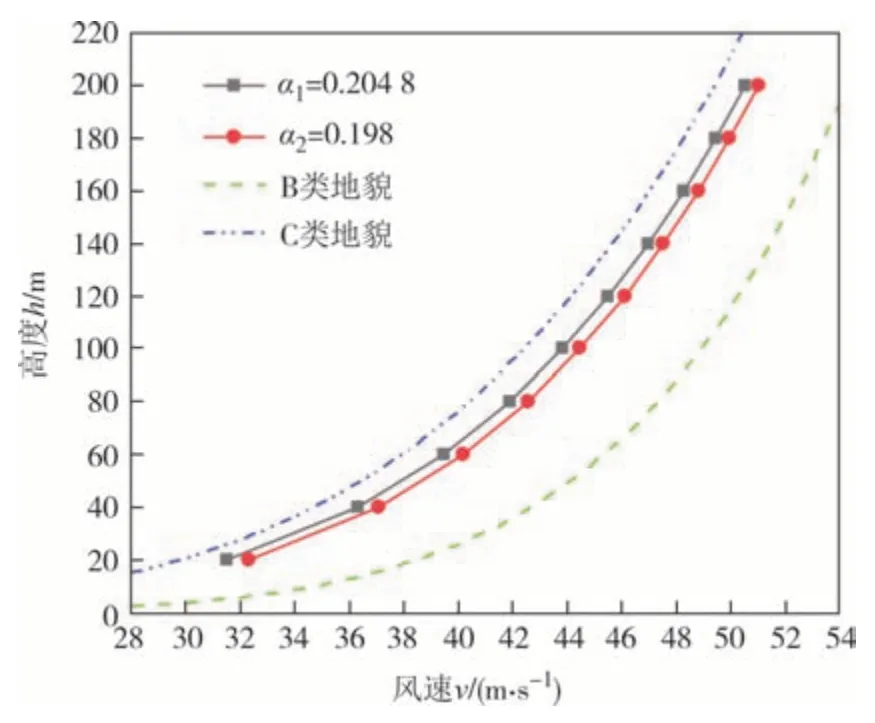
图14 测区一风剖面误差图Fig.14 Wind profile error in test site 1
由表2 可知,在B 类地貌和C 类地貌梯度高度范围内根据地面粗糙度计算出的α2值均为0.196,与风场实测结果之间的相对误差为4.30%.同200 m 高度范围计算结果对比可知,地面粗糙程度对近地面一定高度范围内的风剖面变化规律有较显著影响,采用的计算高度范围不同计算结果略有差异,且计算高度达到一定值时其结果不再改变.
3.2 测区二分析
3.2.1 风场实测α1
测区二风场实测数据经机身修正、归一化处理后,按照指数律进行地面粗糙度指数α的拟合计算,结果如图15所示.
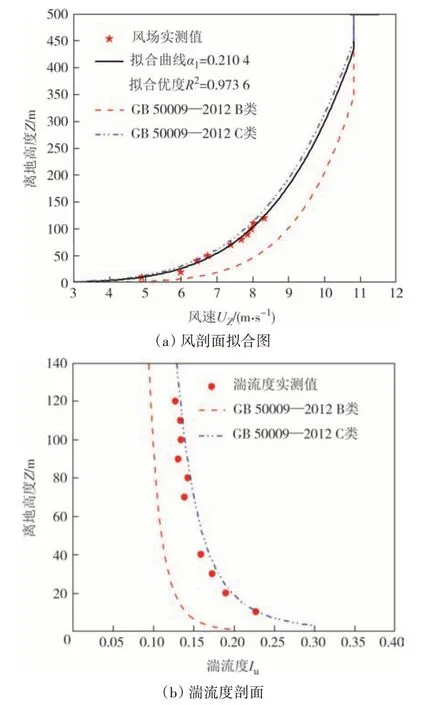
图15 测区二风场拟合Fig.15 Fitting of wind field in test site 2
由图15(a)可知,测区二中实测风剖面拟合指数α1为0.210 4,拟合优度为0.973 6,拟合曲线与C 类地貌吻合程度较高.根据图15(b)可知测区二的实测湍流度数据与规范中C 类地貌非常贴近,同风剖面拟合结果较一致.
3.2.2 地面粗糙度Z0计算
测区二总面积为S2=1 039 631.443 2 m2,所选范围内共计86 处建筑物,对各建筑物进行识别和信息提取如图16 所示.由于该测区存在较多的均匀小区和工厂,其外形相似性较高,故存在部分重叠区域.根据公式(21)计算可得测区二的平均地面粗糙度为:
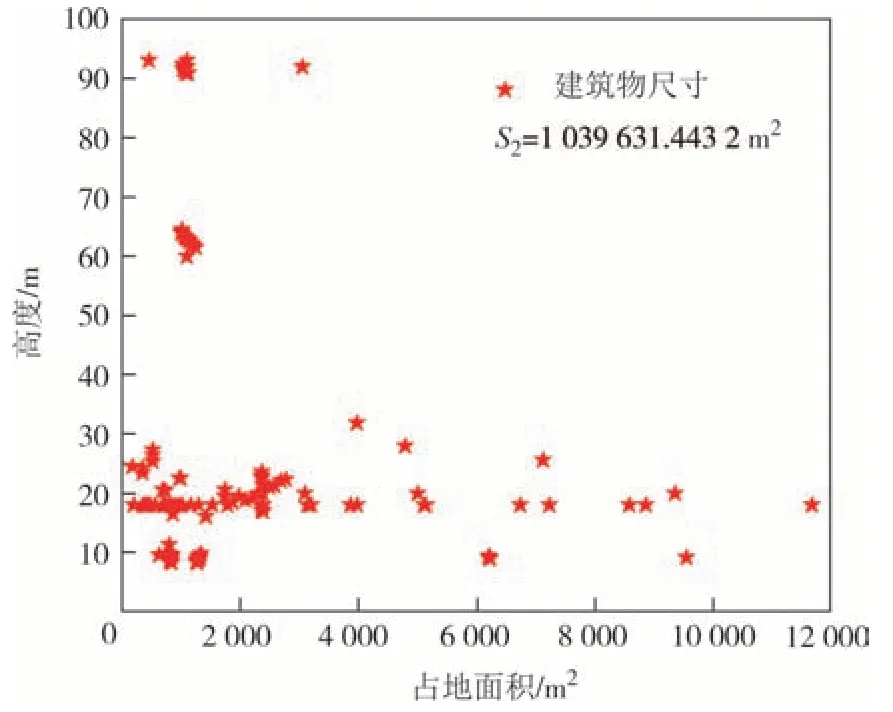
图16 测区二建筑物信息Fig.16 Building information in test site 2
3.2.3 由地面粗糙度Z0计算所得α2
由公式(23)~公式(25)可知,不同的梯度风速值不影响d值随α2的变化规律,即不影响吻合程度最高的α2值判定结果,故本节以梯度风速vG=20 m/s 为例进行计算.
图17 为同一梯度风速下α2在0.150~0.250(精确度为0.001)范围内对应的d值变化曲线,对应于α2=0.206 时d取得最小值.图18 为d取得最小值时两指标对应的风剖面对比图(计算高度范围同上).
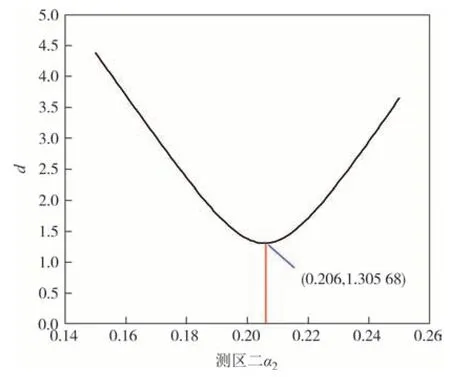
图17 测区二d值变化曲线Fig.17 Change curve of d value in test site 2
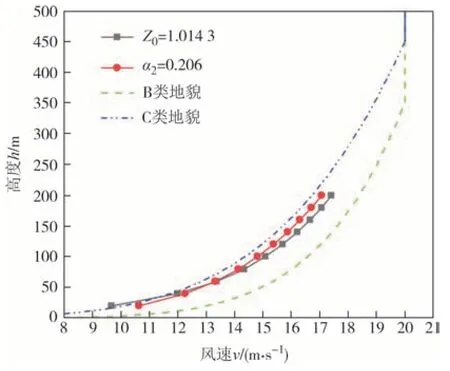
图18 测区二风剖面对比图Fig.18 Comparison of wind profiles in test site 2
3.2.4 误差分析
图19 给出了分别根据地面粗糙度计算所得α2和风场实测得到的α1值在梯度风速均为vG=20 m/s时的风剖面误差图(近地面200 m 范围内).由图19 可知,这两种方法得到的风剖面曲线较为贴近,相对误差为2.09%.分析可知测区二的风场类别介于B、C类之间,分别以不同的梯度高度范围进行计算及误差分析,结果如表3所示.

表3 测区二不同高度误差分析表Tab.3 Error analysis of different heights in test site 2
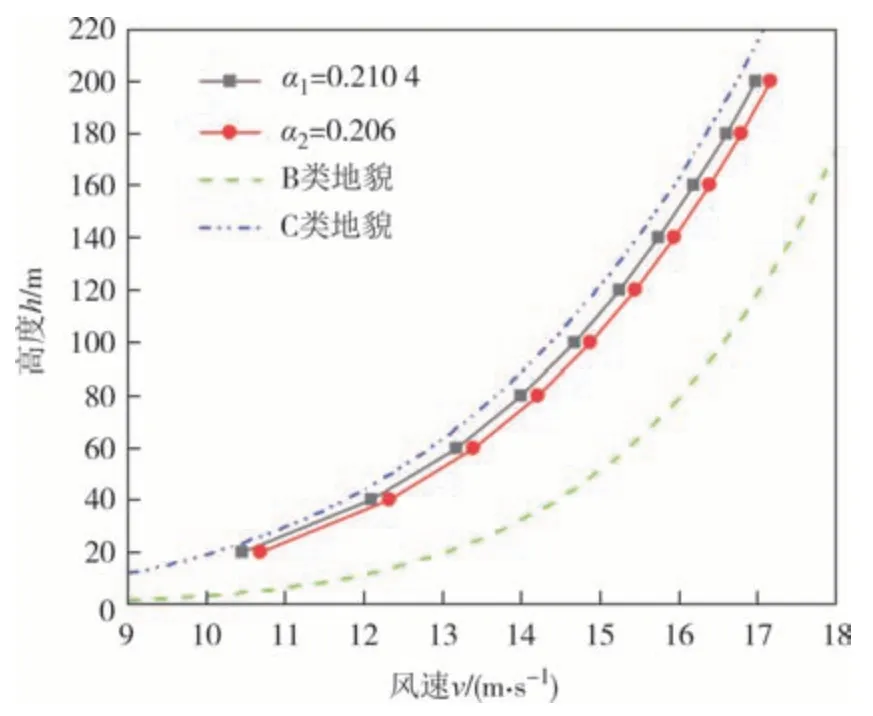
图19 测区二风剖面误差图Fig.19 Wind profile error in test site 2
由表3 可知,在B 类地貌和C 类地貌梯度高度范围内根据地面粗糙度计算出的α2值均为0.203,与风场实测结果的相对误差为3.52%.根据不同高度范围计算结果得到的结论同测区一所得结论一致.
4 结论
本文基于无人机航拍和图像识别方法对城市地区的建筑物尺寸信息进行提取,通过计算出测区内地貌粗糙程度来判定其风场类别,并与空中风场实测结果进行对比,探讨了基于无人机航拍识别城市地区近地风场类别的可行性,经分析得到以下结论:
1)基于无人机航拍和图像识别方法的应用,可快速、高精度地获取建筑物的尺寸信息,进而准确地识别测区内的地貌状况.据此得到的粗糙度指数α值与空中风场实测得到的α值相差不大,两者判定的风场类别一致.
2)按照无人机航拍识别风场类别的方法对近地面不同高度范围进行了分析,采用不同的计算高度范围得到的计算结果略有差异,且计算高度达到一定值时其结果不再改变.根据实际地貌计算得到的粗糙度指数α值与风场实测结果之间的相对误差均小于5%,且计算高度范围与风场实测高度范围越接近两者相对误差越小.
3)本文基于无人机的辅助,提出了一套可靠度高且具有普适性的近地风场类别识别方法,该方法实现了基于实际地貌判定同目标建筑相关的风场类别,研究结果可为城市地区建筑抗风设计提供参考.

