基于光流法和无人机的大型风力机结构动力特性测试
李万润 ,赵文海 ,李家富 ,杜永峰 ,2,3
(1.兰州理工大学 防震减灾研究所,甘肃 兰州 730050;2.兰州理工大学 甘肃省土木工程减震隔震国际科技合作基地,甘肃 兰州 730050;3.兰州理工大学 西部土木工程防灾减灾教育部工程研究中心,甘肃 兰州 730050)
随着人类对不可再生能源的迅速消耗,取之不竭的可再生能源引起人们极大的兴趣.在满足当前和未来的众多可再生能源中,风能因成本低、可持续性强、使用风力发电机对环境影响小等众多优势被认为是最具有前途的可再生能源之一[1].在电力需求日益增长的趋势下,风力发电机作为风能转化为电能的主要形式之一得到了业界的广泛关注和应用.风力机结构损坏不仅会降低其使用寿命和发电效率,还会增加监测误差、安全风险和维护成本[2].因此,风力机的健康监测对其运营和维护具有重要意义.
近年来,基于计算机视觉技术的结构健康监测方法逐渐走进了土木工程领域[3-6],其快速、便捷、成本低等优点可取代传统监测在布线麻烦、信号接收不同步等方面的不足.Dong 等[7]利用多点模板匹配算法提出一种基于视觉的多点结构测量方法,在实验室使用LED 灯和黑点与加速度计进行比较,得到了简支梁的模态信息参数.周云等[8]采用数字图像相关理论方法对结构位移挠度测量,实现以毫米级精度进行结构位移测量.Tian 等[9]利用基于梯度的Hough 变换(GHT)方法提出一种基于非接触视觉测量移动冲击试验方法,在试验悬臂梁上进行模态识别和柔度识别,实现了单摄像机多点动态位移测量.Poozesh 等[10]利用基于相位视频放大和立体摄影测量技术测量了风力机叶片的高频运行形状.
以上研究均为固定相机监测,无法满足大型结构的整体结构监测,无人机的出现解决了固定相机无法灵活移动的弊端,为基于视觉的大型结构健康监测提供了更多的选择.Sony 等[11]首次全面回顾了包括无人机在内的众多新型传感器在结构健康监测方面的应用.Yoon 等[12]利用光流法提出了一种利用无人机拍摄的视频直接进行系统识别的新方法,在估计适当比例因子和补偿卷帘效应的方法降低了对无人机悬停状态下监测结构位移的误差.Hoskere等[13]利用光流法将振动结构的部分模态振型拼接在一起得到全局模态振型,并使用滤波和补偿技术应用于提取位移信号,最后在实验室和室外对比有限元模型与传感器进行了验证.Khadka 等[14]使用搭载数字图像相关(DIC)镜头的无人机对风力机叶片进行了锤击试验,利用DIC 技术得到了叶片的动态特性.虽然无人机可以利用图像最大分辨率对结构位移进行监测,但在近距离下无人机的悬停对所需监测点的位移影响是不可忽略的.针对大型风力机所处环境,风对无人机的影响成为结构健康监测一大挑战.因此在大型风力机结构监测过程中对无人机悬停影响的问题亟需解决.
本文针对大型风力机监测特点提出基于光流法和无人机的大型风力机结构动力特性识别方法。针对无人机空间漂移问题进行研究,提出基于背景不动点结合自适应比例因子的空间位移补偿方法对镜头进行位移补偿,并进行试验验证.结合风力机振动视频与分段监测方法,利用光流法进行风力机结构监测点位移捕捉,测试其摆振与挥舞方向的动力特性.利用无人机的便捷、灵活等优势对风力机进行分段监测,使用分段监测下的局部模态振型计算全局模态振型.
1 基于视觉的位移监测原理
一般基于视觉的位移监测主要可分为相机标定、特征提取、目标跟踪和位移计算四个步骤[4].
1.1 相机标定
镜头畸变会使视觉测量产生不可忽略的误差,因此使用无人机拍摄风力机视频前应对无人机镜头做相机标定得到相机内外参数,再由比例因子将图像坐标转换为物理坐标.本文采用Zhang 标定法[15]对无人机镜头进行标定,由标定得出的相机内参、切向畸变与径向畸变对视频进行校准.通过相机标定方式校准图像畸变可以有效消除图像失真,从而得到更精确的位移测量.
1.2 基于光流法的特征提取及目标跟踪
光流计算是基于物体移动的光学特性提出的两个假设:亮度恒定假设和小运动假设.假设图像上的一个像素点(x,y)在t时刻对应亮度为I(x,y,t),在t+dt时刻的亮度为I(x+dx,y+dy,t+dt),由亮度一致性假设可得:
将式(1)右侧用Taylor展开可得光流基本方程:
式中:u=dx/dt,v=dy/dt分别为图像中像素(x,y)在t时刻x和y方向的瞬时速度.
令Ix=∂(x,y,t)/∂x,Iy=∂(x,y,t)/∂y,It=∂(x,y,t)/∂t,即可转化为光流约束方程:
1981 年由Lucas 和Kanade 提出的Lucas-Kanade(LK)光流法[16]中采用空间一致性假设解决了光流基本方程求解问题.
使用无人机镜头用30 fps 或60 fps 拍摄风力机的振动时,可以将连续的图像视为亮度恒定、运动较小和空间一致,故而满足LK 光流法的基本假设.由于在每个像素点的每一个位置不一定可以求解矩阵的逆,可在算法中使用可逆的角点进行求解.通常在光流法中应用检测器提取特征点为Harris 角点[17],由于Harris 角点采用了高斯滤波,运动速度相对较慢,有角点信息丢失和信息偏移的风险,在光流跟踪中会出现跟踪误差.针对上述问题,J.Shi 在1994 年对Harris 角点算法做了改进,提出一种改进的Shi-Tomasi角点检测算子解决了Harris角点的缺陷,更加适用于光流跟踪[18].本文采用Shi-Tomasi 角点识别目标特征进而识别结构位移,其基本流程如图1所示.
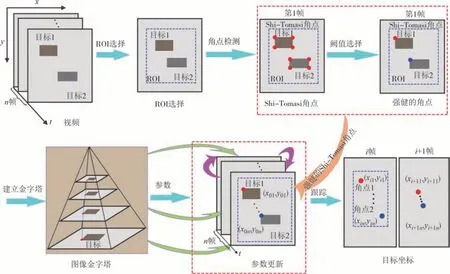
图1 基于光流法的目标跟踪原理Fig.1 The target tracking principle based on optical flow method
1.3 相对位移计算
通过光流法跟踪目标后得出时间序列的每一帧角点相应坐标Pi(xi,yi)与第1 帧角点坐标P0(x0,y0)通过下式可计算结构相对位移dR(单位:pixel):
由于无人机在悬停时自身会出现位移,故而此时识别出的位移为结构相对位移.
2 无人机空间位移补偿
无人机和相机不同之处在于无人机悬停时会产生位移漂移,此类位移漂移出现在空间中且在监测过程中不可忽略.为更好处理位移漂移影响现将空间位移漂移划分为X-Y平面内与Z向平面外分别进行处理,其坐标示意如图2所示.
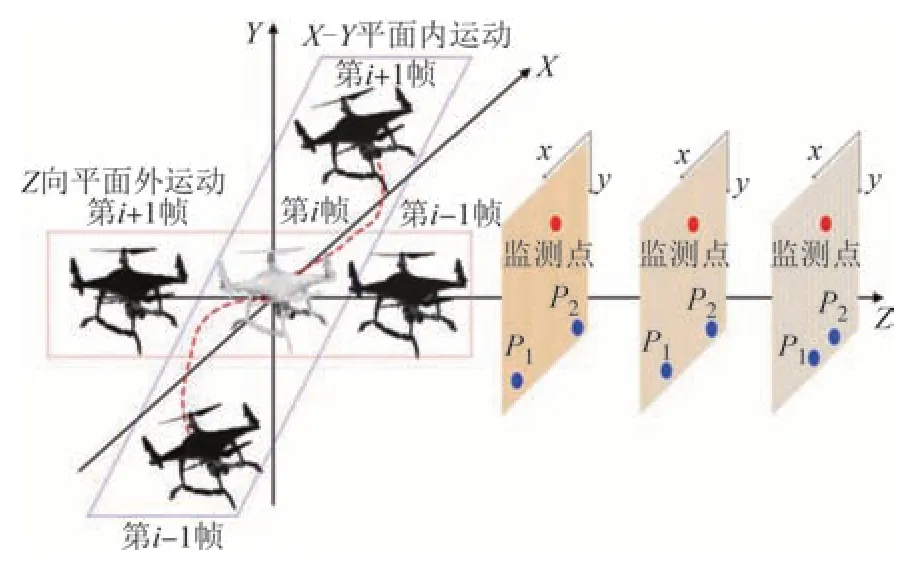
图2 无人机空间位移漂移方向示意Fig.2 The spatial displacement drift direction of the UAV
2.1 平面内位移补偿
对于无人机悬停监测时的平面运动不可忽略的问题,众多学者对无人机悬停问题做出了大量研究.Yoon 等[19]通过实验获得无人机悬停时六个方向位移角度变化.Yoon等[12]和Hoskere等[13]利用高通滤波消除无人机悬停时漂移产生的噪声,但对于0.5 Hz以下固有频率的结构无法准确识别.Perry 等[20]通过相对静止参考目标的相对位移来实现无人机的3C自感知,从而去除无人机的运动,但计算过程复杂不利于快速结构分析.考虑到无人机镜头相对静止参考目标可以反映镜头运动的特性,本文提出基于背景不动点的无人机悬停漂移运动消除的方法,使用对称双圆形标志进行视觉识别,测试试验装置如图3所示.

图3 无人机空间位移漂移测试装置Fig.3 The test device of UAV spatial displacement drift
假设无人机在物理坐标系X-Y平面内运动,以图像帧数作为时间序列,每一帧无人机拍摄位置在X-Y平面内不同,同时监测目标也在此平面内运动.在背景不动点假设下,无人机自身悬停运动时产生的位移漂移可通过此点表示出来.由光流法对监测点和背景不动点同时跟踪,可得出在第i帧下监测点坐标POi(xOi,yOi)和不动点坐标PUAVi(xUAVi,yUAVi),故此监测点的绝对坐标PAOi可表示为:
求得监测点每帧绝对坐标后,由式(4)计算得监测点的绝对位移(单位:pixel).
试验采用缩尺风力机模型给定激励后使其自由振动,由无人机进行位移监测,激光位移计(LDS)进行验证,未经背景点位移补偿的位移时程如图4所示.
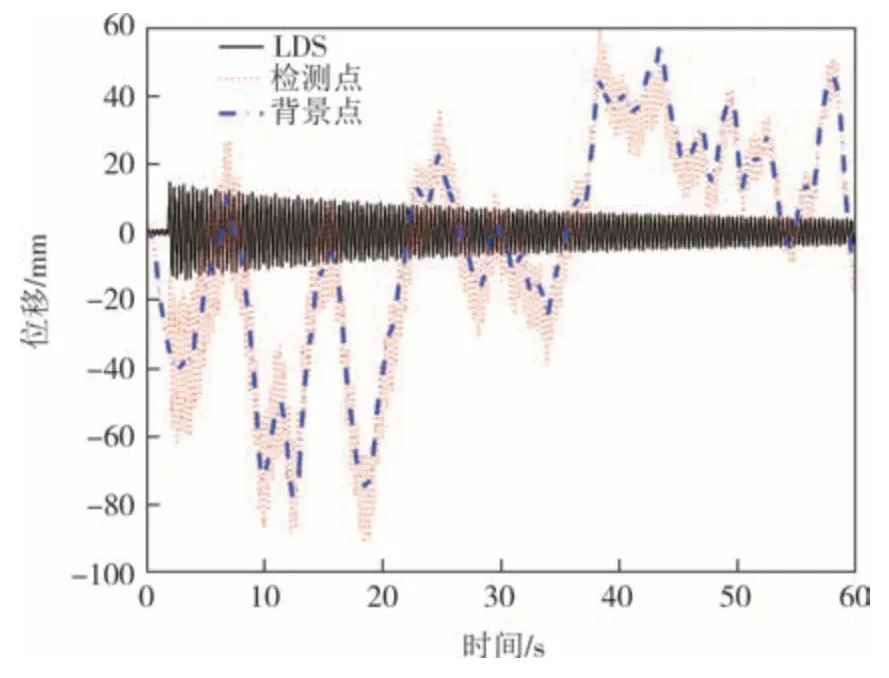
图4 无人机与LDS监测结果对比Fig.4 Comparison of the monitoring result obtained by UAV and LDS
由图4 可知,通过无人机直接监测得到的位移时程由于无人机自身位移漂移显示散乱,无法进行结构响应分析.值得注意的是,背景点的位移增量与结构整体位移响应总体一致,证明了通过不动点补偿无人机悬停时平面内产生的位移漂移的可行性.
2.2 平面外位移补偿
针对无人机空间位移漂移特点,在平面外Z向运动也同样不可忽略,通过平面外Z向补偿位移的同时还可以将像素坐标转换为物理坐标.针对平面外位移漂移现象,现提出一种刚体相对位置不变假设下的自适应比例因子的方法解决无人机平面外位移漂移影响的问题.
假设在结构上或背景中存在某些点随着时间变化其相对位置不发生变化,若无人机悬停监测时只在Z向运动,随着无人机的Z向运动,其比例因子将发生变化.将无人机、手机、相机同时拍摄结构相对位置不变的点60 s,将物理距离与像素距离的比值作为其每帧比例因子,进行归一化操作后如图5所示.
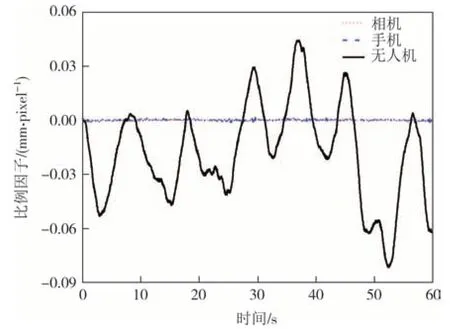
图5 不同设备比例因子对比Fig.5 Comparison of the scale factors obtained by different device
由图5 可知,相机在每帧的比例因子变化幅度近乎于0,手机较相机浮动较大,但仍相比于无人机的比例因子很小,故而相机与手机拍摄时可将自适应比例因子由第一帧确定.由于无人机悬停时在Z向移动,其比例因子每帧变化较大,在本试验中无人机相较于相机比例因子最大误差可达8.32%,因此使用自适应比例因子补偿平面外位移漂移在无人机进行结构健康监测中尤为重要.
通过背景不动点及自适应比例因子将无人机悬停监测时的空间位移漂移进行补偿,使用视觉监测与LDS监测结果对比如图6所示.
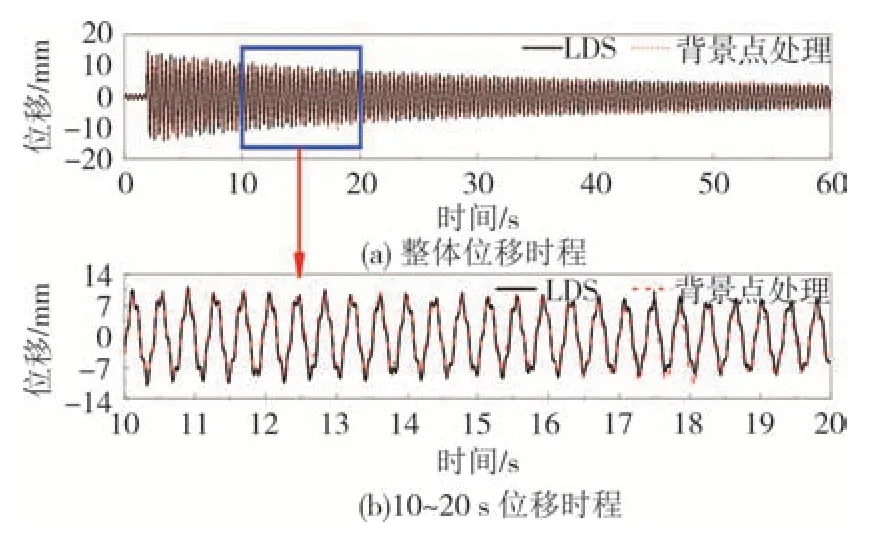
图6 空间位移漂移补偿Fig.6 Compensation of spatial displacement drift
由图6(a)可知,通过背景不动点可有效去除无人机悬停时产生的空间位移漂移.图6(b)为测试过程中10~20 s 的位移时程,从中可以看出通过背景不动点方法整体时程形状较好且细节描绘清楚,虽然幅值会受不动点的位移增量影响导致部分时段偏高或偏低,但整体监测位移与LDS 十分接近,可以在无人机悬停监测时进行位移补偿处理.
由于在实际中风力机在空旷地带,没有完全平行于监测点的背景不动点进行面内位移漂移补偿。对于此类情况,应选取远处背景不动点(如固定建筑物或山脉峰点等)进行计算。此时选取的背景不动点与相机定有一夹角,此时的结构绝对位移可按下式计算:
式中:dRi为在第i帧下实际工程中测量风力机结构的绝对位移;dOi和dUi分别为第i帧下风力机监测点和背景不动点的相对位移;SFOi和SFUi分别为在第i帧下监测点和背景不动点的比例因子;dOpixeli、dOknowi、dUpixeli、dUknowi分别为在第i帧下监测点和背景不动点的像素位移和已知结构距离;θ为背景不动点和镜头的夹角.
2.3 无人机分段监测策略
对于大型结构无法采用单个相机对其进行结构整体监测,且无法在最优监测点实施监测任务.针对此类问题本文利用无人机的灵活性对结构进行分段监测.这种方法可以最大限度地利用无人机的分辨率和振动幅值,进而实现更加精确的结构健康监测.
图7 展示了大型结构监测中使用无人机进行分段监测的原理.首先无人机在大型结构不同位置悬停监测,其次将无人机在不同位置处的监测点进行视觉跟踪及位移补偿,最后通过不同位置的结构响应计算得到振型.
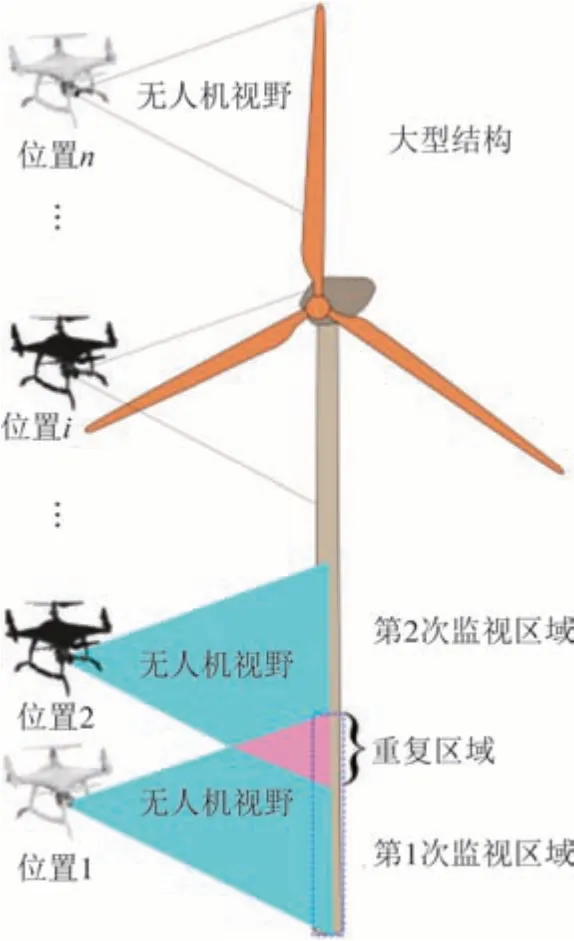
图7 分段监测示意图Fig.7 Schematic diagram of segmented monitoring
无人机对结构分n段监测,其中每段得到m个局部振型,其中Ωi为分段监测的第i个子区域,i∈[1,n],则m阶全局振型为:
式中:Ri为归一化因子,该因子将重叠域中的模式形状缩放为在重叠点处具有相同的值,可使用动态比例因子计算.使用分段监测时为保证其得到全部时间内的自适应比例因子进行振型计算,故监测时必须在相邻监测时间段内图像有重复的部分.虽然此方法得到的结构响应并不同步,但可使用监测重复部分使用归一化因子传递响应,因此对结构的模态参数识别并无影响[13].
归一化因子使用最小二乘最小化方法来获得,最小二乘最小化方法使用线性方程最小化两个向量之间差的平方和.在相邻视野中考虑重叠区域,这些重叠区域中的点的响应用于缩放.如果频域中第1节重叠区域中的点的数据称为A(m,1)的列矩阵中,并且频域中第2 节重叠区域中相同点的变形数据位于B(m,1)的列矩阵中,则关系可以写成:
式中:R是归一化因子.方程的两边可以预先乘以[A]T.
最后可使用矩阵求逆计算最小二乘误差下的归一化因子,如式(9)所示:
将获得的最小二乘误差下的归一化因子([R])乘以频域中第2 节点的变形数据,以便于操作振型的缩放.
3 试验验证
3.1 试验设备
试验采用DJI Phantom 4Pro 无人机,镜头分辨率1 080 P,帧率采用60 fps,LDS 和加速度传感器进行验证.同时为验证基于视觉监测的可靠性,本试验还使用了佳能R6 相机,搭载24~105 mm 变焦镜头和消费级手机摄像头进行试验验证.针对模拟停机下的缩尺风力机模型作振动测试,其试验装置如图8所示.

图8 试验设备图Fig.8 Experimental equipment
3.2 风力机动力特性测试
为验证本文所提方法的可行性,对风力机结构最常见的摆振和挥舞方向振动进行监测,由于叶片振动微小,故而其振动方向仅视为x方向,下文处理数据仅考虑x方向的振动位移.
在缩尺风力机模型叶尖摆振与挥舞方向处施加初始位移而后释放使其自由振动,由LDS 作为基准验证,相机和无人机作视觉验证.无人机在空间内产生的位移漂移由背景不动点结合自适应比例因子补偿,监测得到两个方向的位移时程如图9~10所示.
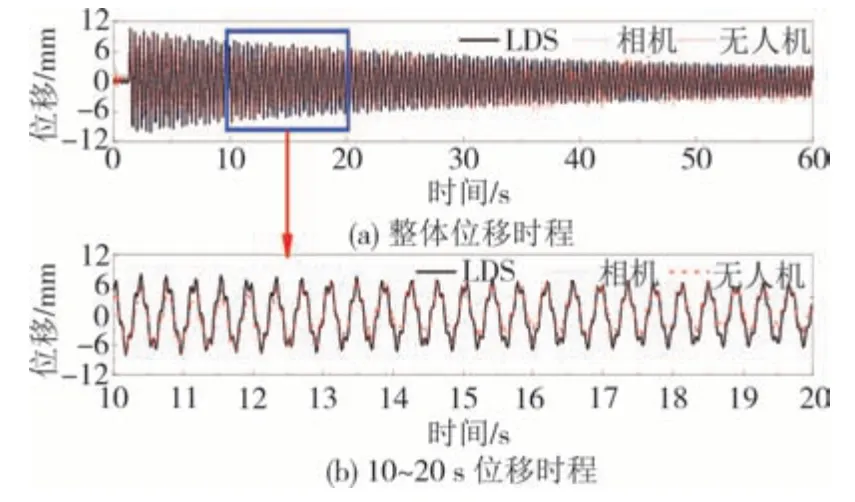
图9 不同设备监测风力机摆振方向位移时程对比Fig.9 Displacement time history comparison of wind turbine edgewise vibration monitored by different devices
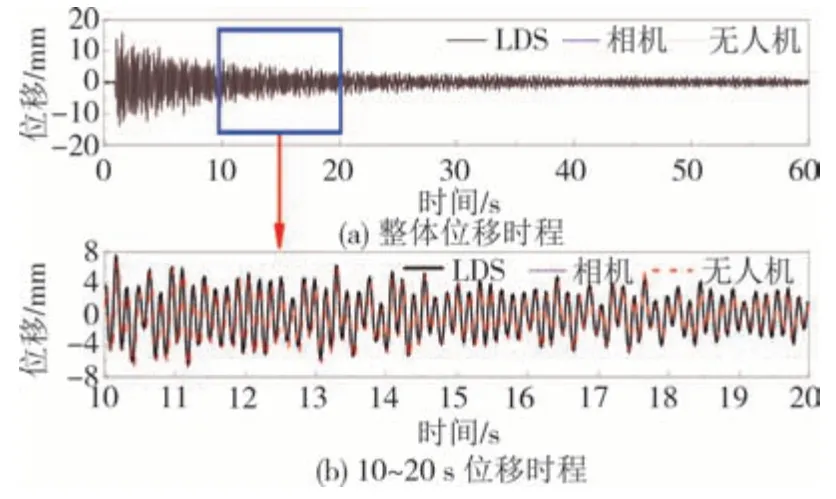
图10 不同设备监测风力机挥舞方向位移时程对比Fig.10 Displacement time history comparison of wind turbine flap-wise vibration monitored by different devices
由图9与10可看出无人机与相机识别结构振动均可行.由于相机是固定的,没有位移漂移,因此相机监测的更加精确,但无人机监测结果与LDS 及相机监测结果曲线基本一致,因此使用无人机对结构进行视觉监测可满足工程需求.将上述时域信号通过快速傅里叶变换为频域信号,其对比如图11~12所示.
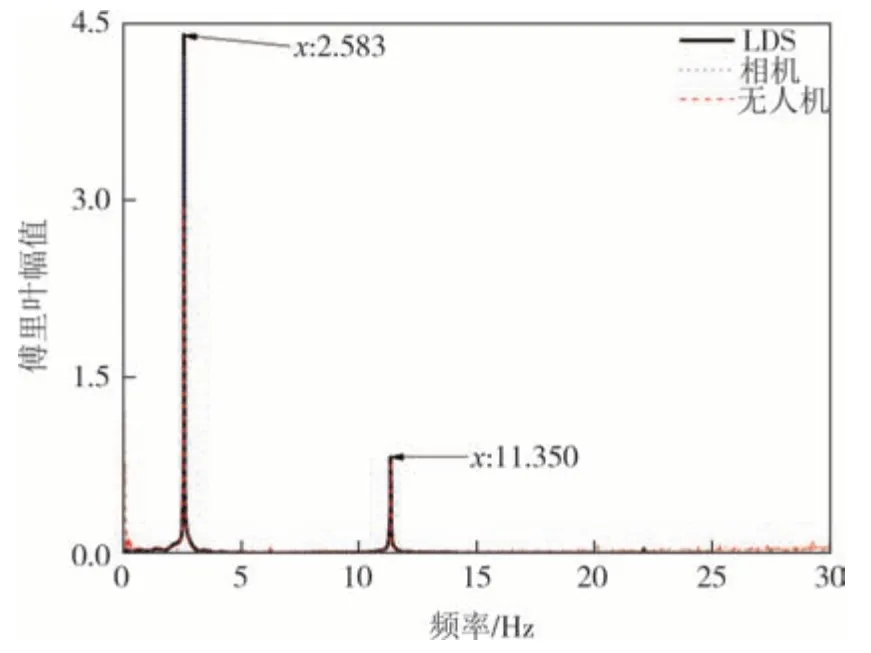
图11 不同设备监测风力机摆振方向频域对比Fig.11 Frequency domain comparison of wind turbine edgewise vibration monitored by different devices
由图11 与图12 可知风力机结构在无人机结合视觉监测系统的结果与LDS 基本一致,不同设备监测缩尺风力机模型摆振和挥舞方向的自振频率如 表1所示,其中以LDS监测数据作为误差分析的基准.
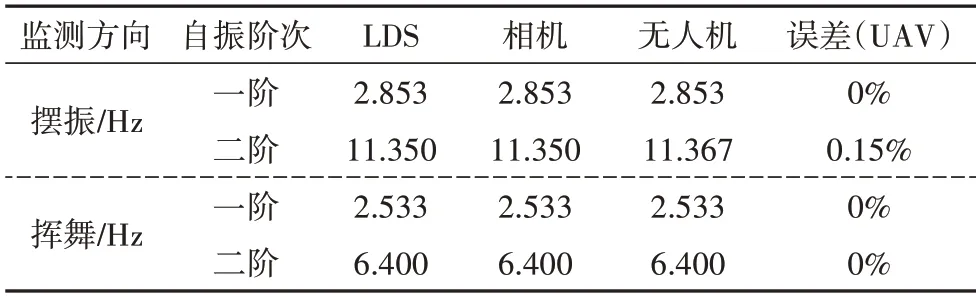
表1 风力机结构摆振和挥舞方向自振频率识别结果Tab.1 Natural frequencies of wind turbine structure in edgewise and flap-wise direction
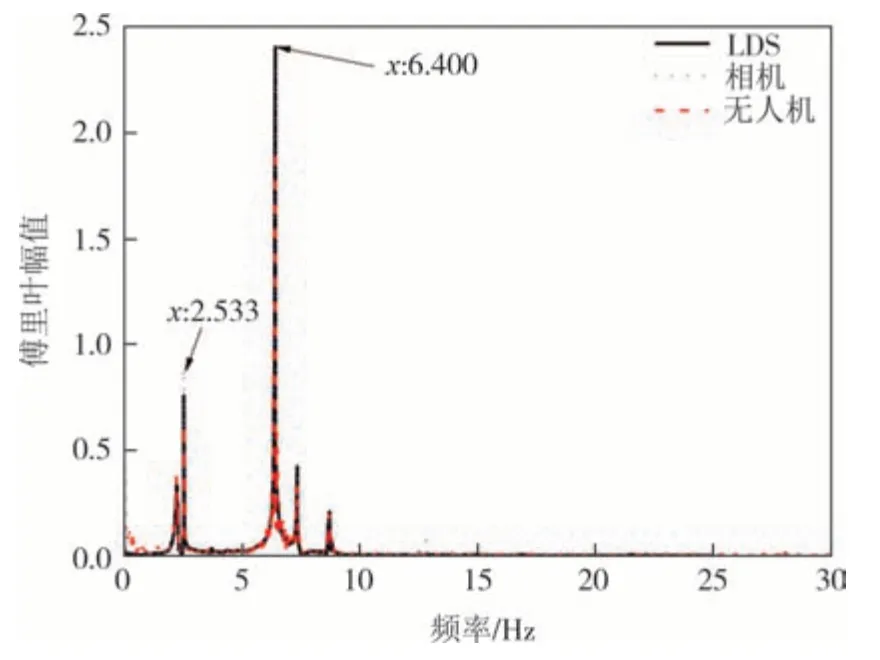
图12 不同设备监测风力机挥舞方向频域对比Fig.12 Frequency domain comparison of wind turbine flap-wise vibration monitored by different devices
3.3 多点监测验证
由于结构健康监测往往是对多个点的监测数据进行分析而得到结构模态参数,因此本次试验验证使用光流法对结构进行多点监测的实用性.试验通过对风力机模型摆振与挥舞方向分别施加激励,监测叶片的叶尖(P1)、叶中(P2)和叶根(P3)的位移验证视觉多点监测的有效性.两次试验分别取60 s 监测其位移时程,监测三点对应位移时程如图13 所示,对应两个方向的位移峰值如表2所示.
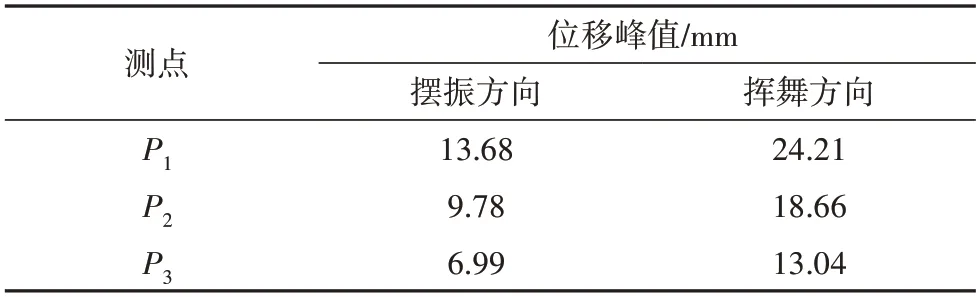
表2 结构多点监测位移峰值Tab.2 The peak displacement of structure at multi-point
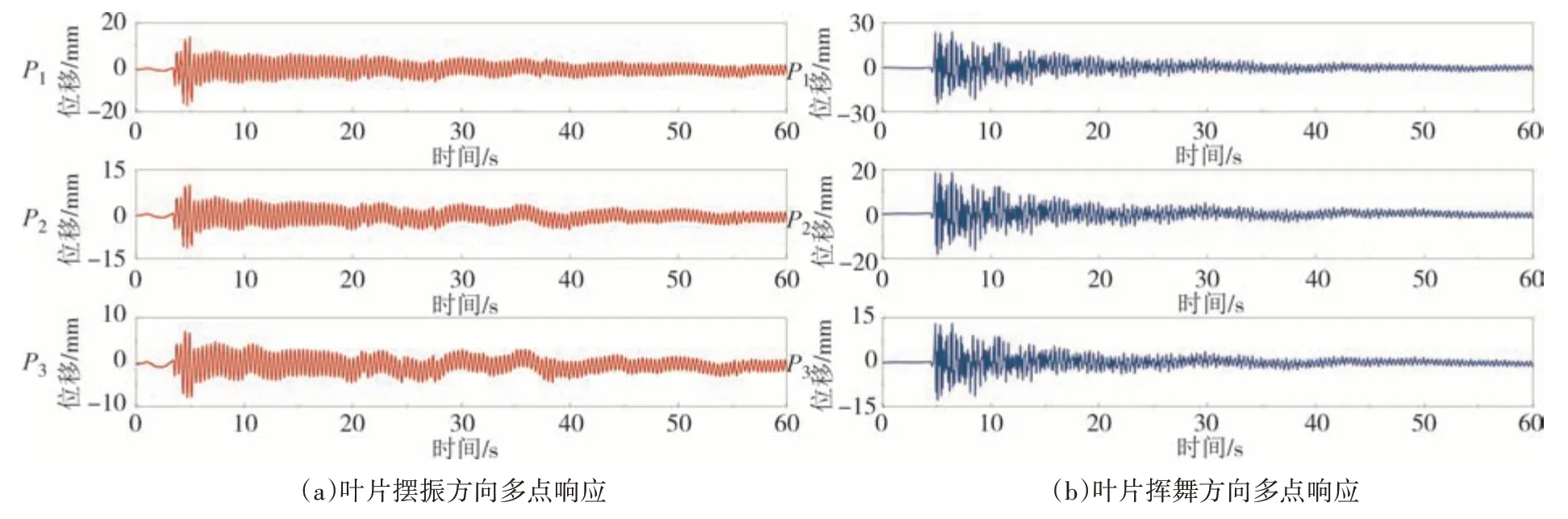
图13 摆振与挥舞方向多点监测结果Fig.13 The monitored results of multi-point in edgewise and flap-wise direction
由图13 可知,在摆振和挥舞两个方向监测对应叶尖、叶中与叶根的位移时程的规律一致,且在表2展示的位移峰值依次减小,符合振动规律.在图13中可明显看出摆振方向P1、P2、P3的位移趋势仍有无人机自身运动影响,其原因在于选取的背景不动点更加接近P1,但P1的位移补偿并不完全满足于其他监测点,故而出现无人机自身位移漂移影响监测的现象.本次试验验证了基于视觉的方法在多点监测结构的可行性,且视觉容易更换所需监测点,进而可实现结构的全场监测.为实现更加精确的监测,应在监测过程中尽量将背景不动点选择离监测点较近的位置.
针对加速度传感器安装的不便性,试验利用视觉与无人机对结构进行监测,同时采用加速度传感器与LDS 验证视觉的准确性.对风机模型摆振和挥舞方向快速施加连续激励,使用视觉、加速度传感器与LDS 测试风力机频域信息.测得三种不同设备在摆振和挥舞两个方向的功率谱密度如图14 所示,为了更好地对比显示,横轴采用对数尺度.
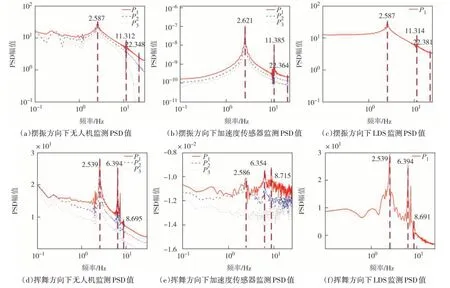
图14 摆振和挥舞方向频率测试结果Fig.14 The test results of frequency in edgewise and flap-wise direction
由图14 可知,在摆振与挥舞方向视觉与LDS 可以明显识别到第一与第二阶自振频率,尤其在挥舞方向,第三阶自振频率加速度传感器识别得更好,而视觉与LDS 较难以识别.这种结果是合理的,因为加速度传感器天生对高阶振动敏感,而位移传感器对低阶振动更加敏感.以加速度传感器为基准对比视觉传感器和LDS 的准确率,其中摆振与挥舞方向自振频率与误差如表3所示.
由表3 可知,不论是在摆振还是挥舞方向,以加速度传感器测得的自振频率为基准误差随着阶次的增加而越小,符合加速度传感器的监测特点.表3 中所测自振频率与加速度传感器对比下最大误差不超过1.29%,自振频率测试准确率可达98.71%以上,可以满足工程需求,因此可以利用无人机结合光流法代替加速度传感器进行大型结构动力特性测试.
由于使用无人机进行结构动力特性监测,其镜头不受传统相机监测的距离影响,可在距离实际监测结构的1~2 m.因此,在实际工程中,视觉测试精度与结构的距离虽然成比例关系,但无人机不受其限制,故此最大误差将在2%以内.
3.4 风力机结构振动台测试
为验证分段监测方法的有效性,将无人机悬停于风力机结构前1.5~2 m,自上而下分2段进行监测,使用振动台激发结构响应.试验分为摆振与挥舞两个方向振动.无人机共悬停2次,每次悬停12 s,视觉自下而上分为P0~P9共10 个监测点且分别设置对应背景点验证,其中P4与P5为两次监测的重复测点.使用相机全局监测进行视觉验证,对应在P0、P2、P4、P7与P9使用加速度传感器验证,由于篇幅关系,仅展示摆振方向的结构响应如图15所示.
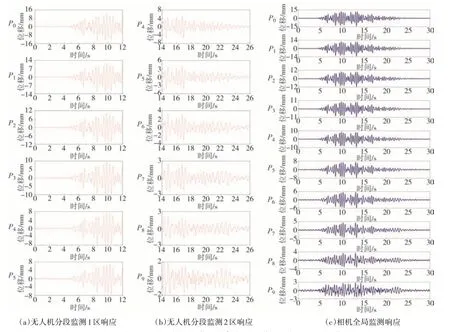
图15 摆振方向无人机分段监测与相机全局监测结构响应结果对比Fig.15 Comparison of the structural response results obtained by UAV segmented monitoring and camera global monitoring method in edgewise direction
由图15 可知,使用无人机在监测1 区监测12 s后经2 s 悬停至监测2 区再进行监测,因此监测2 区从14s开始监测.与相机全局监测对比分段监测对比可知,采用每个视觉监测点对应一个背景点的监测效果更好,因此视觉结合无人机可以更加方便有效地进行视觉监测任务.图15 中使用无人机分段监测时采用P4及P5作为重复部分计算归一化因子,再由式(9)计算全局模态振型如图16所示.
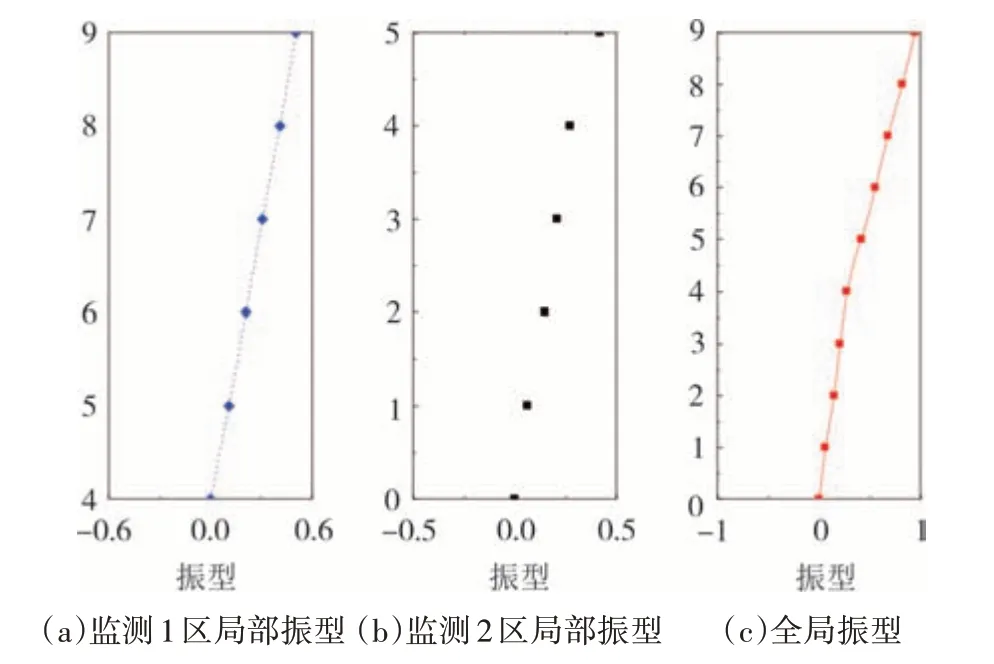
图16 局部与全局模态振型Fig.16 The local and global mode shapes
由图16 可知,分段监测1 区与2 区得到的局部振型由P4与P5点计算归一化因子可缝合得到全局振型,分段监测方法可用于全局振型计算.风力机摆振与挥舞方向使用振动台测试且使用相机与加速度传感器对比,得到的全局振型如图17所示.
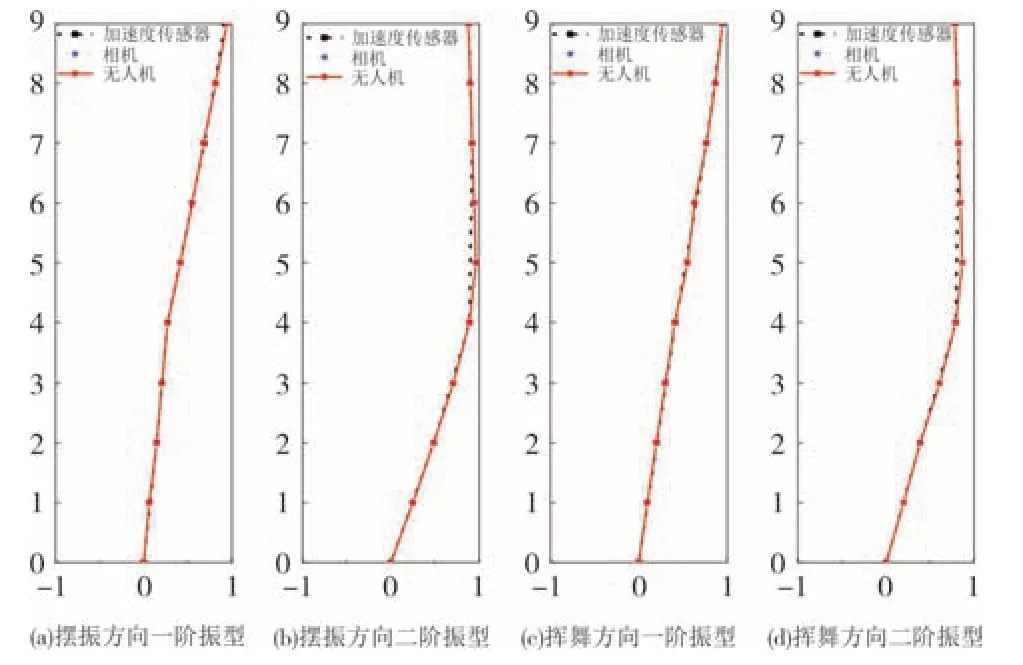
图17 风力机振型Fig.17 Wind turbine structure mode shapes
由图17 可知,视觉与加速度传感器计算得到振型基本一致,使用分段监测计算的全局振型与相机监测计算一致,因此使用分段监测对大型风力机结构进行模态计算机分析具有可行性.相比于相机,无人机的机动性更强,因此在视觉监测中仅使用一台无人机即可完成对风力机结构的结构动力特性监测.且由于视觉可以监测更多的测点,故而得到振型更加平滑,更利于结构动力特性分析.
4 结论
通过背景不动点结合自适应比例因子方法补偿无人机空间运动时产生的位移漂移,采用光流法和无人机对风力机进行视觉位移跟踪监测,结合分段监测方法识别风力机结构的动力特性,经试验验证与结果分析,可以得到以下结论:
1)通过基于背景不动点结合自适应比例因子提出无人机空间位移漂移的补偿方法,可用于无人机悬停监测时去除空间位移漂移影响.
2)使用光流法和无人机对风力机结构位移相应测试,可对结构多点同时监测,且与高频较敏感的加速度传感器在频域对比精度可达98.71%,满足实际工程需求.
3)结合分段监测方法对大型结构进行动力特性测试,在最大化利用无人机的便捷、灵活等优势的同时,使用分段监测下的局部模态振型计算全局模态振型,与相机的全场监测得到的振型一致.因而仅使用一台无人机即可对大型风力机为代表的高耸结构的动力特性测试.

