中国传统火炕非均质设计与性能优化

李洪强 ，毕名达 ，阳小华 ，刘丽芳 ，周彦 ，徐峰 ，张国强

［1.湖南大学 土木工程学院，湖南 长沙 410082；2.建筑安全与节能教育部重点实验室（湖南大学），湖南 长沙 410082；3.湖南大学 国家级建筑安全与环境国际联合研究中心，湖南 长沙 410082；4.湖南大学设计研究院有限公司，湖南 长沙 410082；5.湖南科技大学 土木工程学院，湖南 湘潭 411201；6.湖南大学 建筑与规划学院，湖南 长沙 410082］

随着人民生活水平的提高，人们对建筑室内环境的要求越来越高，极大地增加了建筑能源消耗.其中，全国建筑业一次能源消耗占全国能源消耗的36%，而城市居民住房和农村住房占到了总建筑的1/4［1］.根据中国居住建筑采暖规范相关说明，集中采暖主要在北方地区，截至2020 年城市集中供热面积已达98.82 亿m2［2］，集中供热大幅度改善了城市居民的生活、工作环境，但并未完全覆盖农村地区.

农村居民分布具有人口密度低、居住分散等特点.南方部分地区冬季室内温度低，使用火桶等取暖设备［3-4］.北方农村地区主要采用分散式的局部供暖形式——火炕、土暖气等，此类供暖方式存在能效低、污染严重等诸多问题.如：土暖气主要使用煤炭作为能源，而农村居民所获得的煤炭大多是劣质散煤，使用低质量的散煤被认为是北方农村大气污染的主要原因之一［5-6］.

中国北方农村供暖应用范围更广的是传统火炕，该种供暖方式具有较多优势：传统火炕的制作简单，可以就地取材，且主要由土质构成，热惰性好，拥有一定的热舒适性［7］；传统火炕及其配套炉灶可以满足烹饪、就寝、供暖的多重需求［8］.当前，我国农村建筑虽然有多种采暖方式，传统火炕依然是中国北方乡村重要的文化符号，发挥着不可替代的作用［9］.

相关学者对传统火炕进行了大量研究工作.He等［10］优化太阳能炕的性能，并基于预测平均投票对太阳能炕的睡眠热舒适环境进行了评估.戴天钊［11］提出一种相变蓄热式太阳能炕，并运用Fluent 对炕进行优化，通过试验得出合理的太阳能炕运行参数.Gao 等［12］运用热力学理论建立炕供暖房间的动态热数学模型，并运用其预测房间温度.Bian［13］基于Fluent 建模获得不同外界条件下，炕供暖室内的温度场变化情况.

但目前传统火炕应用尚存一定问题［14］，如：热效率低、环境污染大、炕面温度分布不均［15］.其中，炕面温度的均衡度是直接影响农村居民生活的关键因素.由于传统火炕结构、烟气温度、制作材料等因素的限制，炕头温度可达60～70 ℃，炕尾温度又过低，使人产生极大的不舒适感，农村的围护结构保温性能不佳，在这样的情况下，传统火炕的供暖效果进一步降低［8］.

针对火炕炕面温度均衡性问题，王丹等［16］提出采用倾斜炕板来改善炕面温度的不均匀性，并对不同倾斜度炕板的落地炕和吊炕进行数值模拟研究，结果表明：炕头黏土厚度80 mm，炕梢黏土厚度20 mm 时具有相对最优的换热性能与采暖效果.芦欣［17］通过试验得出节能型吊炕的热工性能，建立数值模型并对节能型吊炕的性能进行研究.结果表明，炕板倾斜放置、炕头炕尾不同的蓄热层厚度均可以降低炕面温度的不均匀性.张茜［18］对东北传统民居少数民族弯曲炕、满屋炕建模并进行数值模拟，研究得到满屋炕、弯曲炕的合理运行参数.Yu等［9，19］对目前的炕的形式、烟道结构、换热性能进行总结分析，客观评价近年来新提出的炕形式，并提出若干研究点.尽管很多学者对传统火炕的传热过程［20-22］分析建模，但并未定量地对传统火炕的内部结构与上散热面进行研究，传统火炕还存在炕面温度不均、热舒适性差等问题［23］.

为此，本文提出中国传统火炕非均质设计方法，通过传统火炕内部结构与炕板蓄热层的非均质设计与烟气流场的优化，使传统火炕的炕面温度更加均匀，以提高传统火炕供暖的舒适性.借助计算流体力学（Computational Fluid Dynamics，CFD）分析平台，对非均质设计中国传统火炕进行建模，分析关键设计参数——竖洞率、炕板蓄热层厚度、入口烟气温度、烟气出入口位置对烟气流动和传统火炕热性能的影响规律.本文对传统火炕的改进提出了定量分析方法，为中国传统火炕供暖改进提供了新思路.

1 中国传统火炕非均质设计方法

1.1 传统火炕温度场失衡影响因素

传统火炕内部烟气流动的同时向炕体传热，使火炕温度升高，烟气温度降低.由基本传热规律可知，炕板表面温度场必然出现炕头温度高、炕尾温度低的情况.由此可以分析，传统火炕的失衡因素有以下几点：

1）火炕内部结构不合理，导致烟气局部滞留，炕面产生局部的高温区.

2）火炕上散热面厚度不合理，合适厚度的散热面有助于降低炕头的高温，提高炕尾的温度，提高炕面温度均衡性.

3）火炕蓄热能力不强，加热后很快冷却，无法长时间供热.

本文针对上述问题提出两种优化方法：传统火炕内部结构非均质设计和传统火炕上散热面非均质设计.并运用统计学原理，使用炕面温度标准差来评价炕面温度的均匀程度［15］：

式中：D为炕面温度标准差，℃；xi为炕面测点温度，℃为炕面温度平均值，℃；n为炕面测点个数.

1.2 传统火炕温度场优化——非均质设计方法

1.2.1 传统火炕非均质设计——内部结构非均质设计

传统火炕具有竖洞、横洞、花洞等内部结构形式，如图1 所示.传统火炕的内部支柱具有支撑炕板、蓄热、改变烟气流场的作用.其中，改变烟气流场可以进一步影响火炕的热过程，因此合理安排支柱的摆放位置，可以改善火炕的温度场.

图1 传统火炕内部结构［18］Fig.1 Internal structure models of traditional heated Kang

本文提出内部结构非均质设计方法：在烟气入口附近（炕体前端）降低烟气流动阻力，烟气快速地通过该区域，减少传热时间，可以降低炕头温度；在烟气出口附近（炕体后端）适当地增加流动阻力，增强传热，利用炕支柱的蓄热特性，可以提高炕尾的温度.竖洞区域的支柱摆放方向与烟气流动方向相同，阻力较小，横洞区域的支柱摆放方向与烟气流动方向垂直，阻力较大，所以将竖洞区域集中在烟气入口，横洞区域集中在烟气出口，有效地控制烟气在传统火炕中的流动过程，改善火炕表面的温度均衡性.

由图1 可知，花洞形式为横洞与竖洞以一定的比例组合而成，本研究将竖洞区域占火炕整体区域的比例称为竖洞率，如图2所示，计算公式见式（2）.

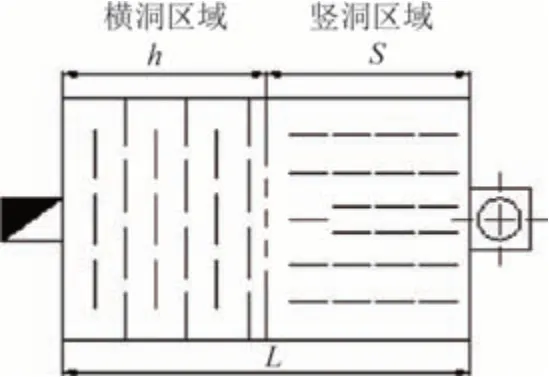
图2 传统火炕内部结构非均质设计方法Fig.2 Heterogeneous design method for the internal structure of the traditional Kang

式中：S为火炕中竖洞区域的长度，m；L为火炕的总长度，m.

根据上散热面分区和内部结构非均质设计方法综合考虑，本文对上述花洞火炕模型进行适当的简化，图3 为简化后的新型多区花洞火炕模型，并且用作后续研究.

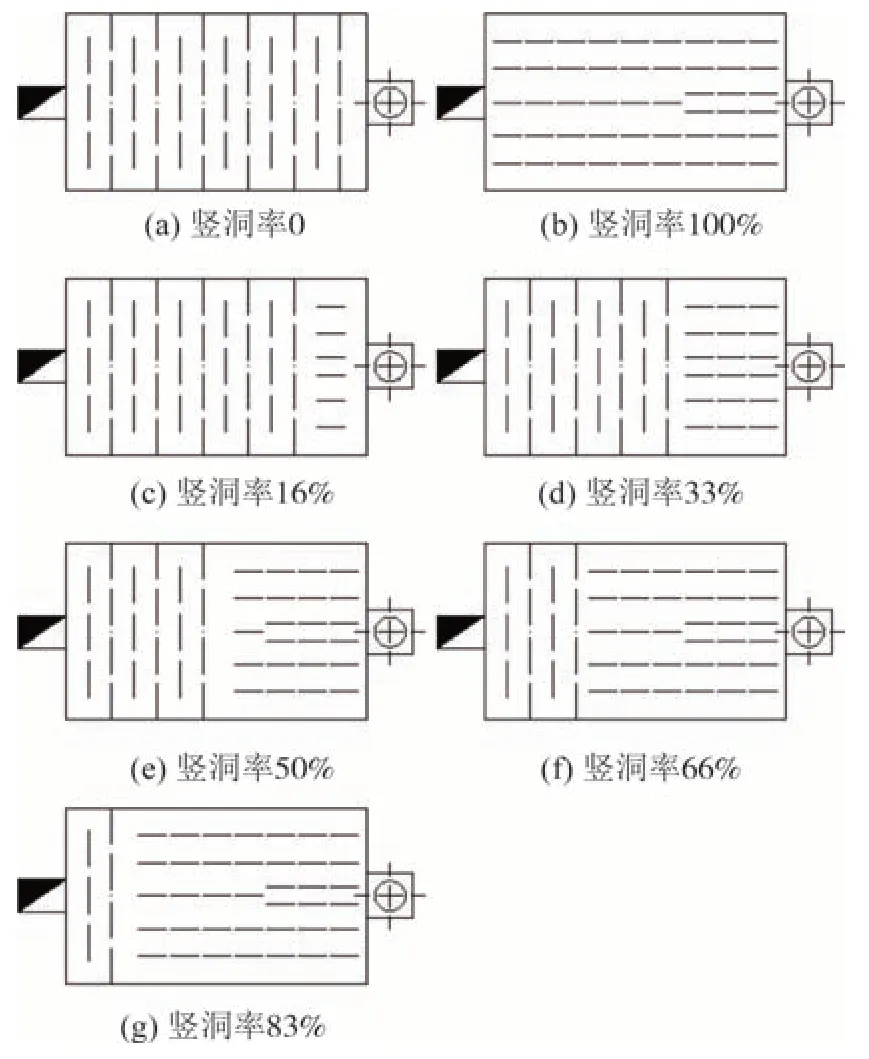
图3 新型多区花洞火炕模型Fig.3 Models of the new mixed-mode flue Kang

1.2.2 传统火炕非均质设计——上散热面非均质设计

传统火炕最大的散热面是上散热面，上散热面也是直接与人体接触、对人体影响最大的散热面，因此本文优先研究上散热面的非均质设计，权衡考虑火炕的经济性与施工的容易度，本文提出了将上散热面分成三个区域进行非均质设计.

图4 为本文所提出的新型火炕上散热面非均质设计结构示意图.本文提出上散热面非均质设计方法：将火炕炕面分为三个区域，分别是距离烟气入口较近的Ⅰ区、中间区域Ⅱ区和距离烟气出口较近的Ⅲ区.增加Ⅰ区的炕板蓄热层厚度，减小Ⅲ区的炕板蓄热层厚度，使得Ⅰ区炕板具有更大的传热热阻，降低Ⅰ区炕面温度，Ⅲ区炕板具有更小的传热热阻，提高Ⅲ区炕面温度，最终达到控制炕面温度均衡性的目的.

2 非均质设计中国火炕模型建立及求解方法

2.1 物理模型

本文以中国典型火炕的尺寸为案例进行建模，非均质设计中国火炕内壁尺寸为长（L）×宽（W）×高（H）=5 m×2.1 m×0.5 m.

根据中国传统火炕的使用情况，它与周围环境的热量交换主要是通过火炕与室内空气的自然对流、炕与炕内烟气的对流、炕与室内外物体的热辐射、炕与地面的导热，因为中国火炕内部的传热条件比较复杂，本文对火炕的热过程进行如下假定：

1）忽略烟气夹带的杂质固体颗粒；

2）烟气入口流量相对固定；

3）忽略火炕的炉灶和烟囱部分；

4）火炕的传热过程为稳态过程；

5）火炕下垫面为绝热；

6）火炕围护结构的传热系数恒定；

7）忽略烟气的辐射作用.

2.2 数学模型及求解

2.2.1 控制方程

火炕烟气的流动遵循着质量、动量和能量守恒定律.

1）质量守恒方程可以写成如下形式：

式中：ρ为密度，kg/m3；v为速度向量，m/s；Sm为广义源项，W/m3.

2）惯性参考系中的动量守恒方程可以写成如下形式：

式中：p为静压力，Pa；τ为应力张量，Pa；ρg与F分别为重力与外力，N.

式（4）中应力张量τ为：

式中：μ为动力黏度，Pa∙s；I是单位张量，Pa.

3）Fluent求解的能量方程为以下形式：

式中：T为温度，K；λ为导热系数，W/（m∙K）；Sm为广义源项，W/m3；u、v、w分别为烟气在x、y、z方向上的速度，m/s；cp为定压比热，J/（kg∙K）.

2.2.2 求解方法

采用限制较小的DO 辐射模型，采用Realizablek-ε湍流模型，选择标准壁面函数.离散化方法为二阶迎风格式，压力速度耦合算法为SIMPLE算法.

2.3 边界条件及热物性参数设置

2.3.1 边界条件设置

火炕与外界环境的换热主要由与围护结构的辐射和与空气的对流传热两部分组成.

火炕的对流换热系数可以用公式（7）计算.

式中：Nu为火炕自然对流换热的努谢尔特数；l为特征长度，m；λ为定性温度下的空气导热系数，W/（m∙K）.

式中：C和n为由实验确定的常数；Gr为定性温度下的格拉晓夫准则数；Pr为定性温度下空气的普朗特准则数.

式中：g为重力加速度，m/s2；α为流体容积膨胀系数，1/K；Δt为流体与壁面温度差，K；ν为定性温度下空气运动黏度，m2/s.

由牛顿冷却公式可以得到火炕辐射换热系数的计算公式：

式中：hr为辐射换热系数，W/（m2·K）；Cb是黑体辐射系数，取5.67 W/（m2·K4）；ε为火炕体表面发射率；Tm为散热面外表面温度，K；Tam为环境中围护结构温度，K；tm为散热面外表面温度，K；tf为室内空气温度，K.

对流换热系数与辐射换热系数可以综合为复合换热系数：

经上述过程计算，中国火炕的室内侧面复合换热系数为9.18 W/（m2·K），室外侧面复合换热系数为8.26 W/（m2·K），炕面复合换热系数为10.81 W/（m2·K）.入口边界为速度入口，出口采用自由出流边界，下垫面为绝热表面.

2.3.2 材料物性参数设置

材料热物性参数如表1所示.

2.3.3 网格划分及无关性验证

表2 为不同网格数下的炕面温度情况.本研究划分了网格数为136 896、286 740、903 900（网格尺寸分别为0.04 m、0.03 m、0.02 m）三套结构化网格，相对误差小于2%.经计算，本文认为模拟结果与网格尺寸无关.

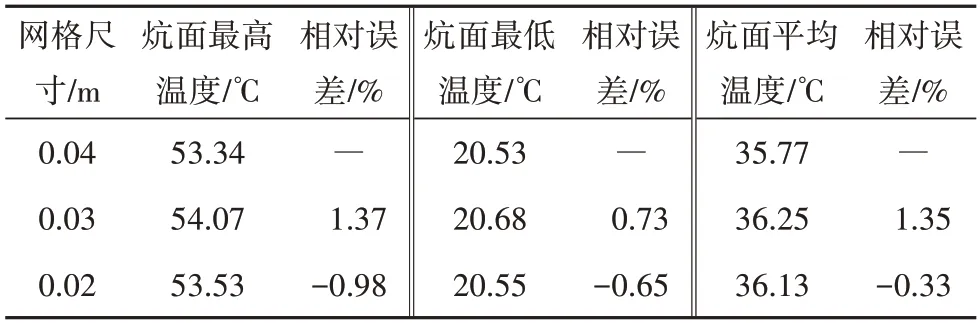
表2 网格无关性验证Tab.2 Grid independence verification

3 计算结果与讨论

3.1 烟道竖洞率与炕内烟气流动和炕面温度关联特性

图5 为不同竖洞率下的炕面温度云图及高度为0.32 m 的平面上的烟气流线图.炕面高温区主要集中在竖洞刚刚转变为横洞的区域（以下称为转变区）以及炕头烟气入口附近的区域.转变区炕面温度较高是因为炕支柱的蓄热特性，以及烟气被横洞区域的支柱阻挡、扰动，烟气在转变区堆积加强传热，最终导致转变区炕面温度升高.炕头烟气入口附近炕面温度较高的原因是烟气入口处烟气温度最高，换热温差最大.

在竖洞率为0～50 %时，炕面的低温区域集中在炕尾部分；而竖洞率为50%～100%时，炕面的低温区域集中在炕头部分，低温区域在火炕长度方向上的分布刚好与转变区的分布相反.

在烟气入口、出口处具有较大流速，其余部分烟气流速较小.在各个模型中的横洞区域均具有旋涡，竖洞区域存在回流.结合温度云图与烟气流线图，可得Ⅱ区中间位置的炕支柱发挥较强的蓄热作用，提高了Ⅱ区的炕面温度.

图6 为不同竖洞率情况下的炕面最低温度与平均温度情况.竖洞率从0～100%，炕面平均温度从42.2 ℃降低到34.2 ℃，降幅为19%.炕面最低温度先升后降，在竖洞率为33%时达到最大值24.1 ℃.竖洞率从0 增至33%，炕面最低温度从21.5 ℃升高到24.1 ℃，增幅为12.1%；竖洞率从33%增至100%，炕面最低温度从24.1 ℃降低到19 ℃，降幅为21.2%.

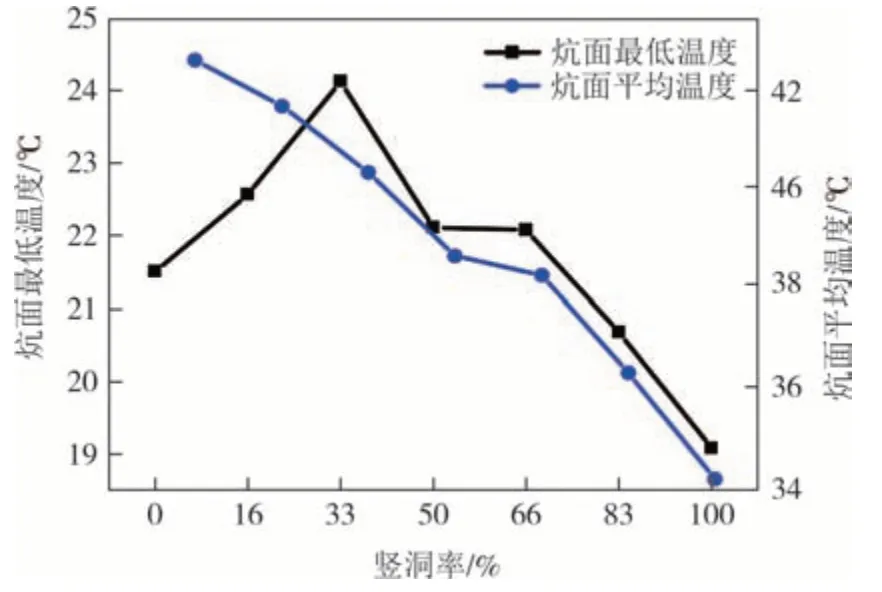
图6 竖洞率与炕面平均温度和炕面最低温度的关联特性Fig.6 Influence of VHR on average temperature and minimum temperature of Kang surface

结合图5 和图6，可得竖洞率较低时，炕面最低温度出现在炕尾，竖洞率越低，炕面最低温度越低.相反，竖洞率较高时，炕面最低温度出现在炕头，竖洞率越高，炕面最低温度越低.

图7 为不同竖洞率情况下，炕面温度标准差和炕面最高温度的变化图.随着竖洞率的增大，炕面最高温度从74.9 ℃降低到52.9 ℃，降幅为29.4%；炕面温度标准差从12.2 ℃先降低到最小的6 ℃，随后升高到6.5 ℃，在竖洞率为83 %时达到最小值.

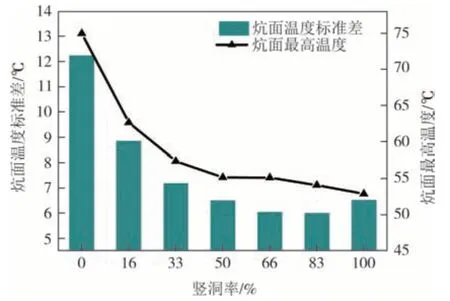
图7 竖洞率与炕面温度标准差和炕面最高温度的关联特性Fig.7 Effect of VHR on the standard deviation of Kang surface temperature and the maximum temperature of Kang surface

竖洞率为0～50%的情况下，炕内的横洞支柱会使烟气在炕头区域长时间停留，导致炕头区域温度过高，且炕面温度标准差也会很高.而竖洞率为1 时，烟气在烟道内的滞留时间过短，导致炕尾温度较低，炕面温度不如83%竖洞率的情况均匀.83%竖洞率的情况炕面温度均匀性最优，本文采用83%竖洞率进行后续的研究.

3.2 入口烟气温度与炕面温度关联特性

图8 为入口不同烟气温度下，炕面温度标准差、炕面最高温度和炕面最低温度情况.随着烟气温度升高，炕面温度标准差、炕面最高温度和炕面最低温度均增加.烟气温度从200 ℃增加到350 ℃过程中，炕面温度标准差从4.2 ℃增加到7.9℃，增幅为88.1%；炕面最高温度从38.6 ℃增加到74 ℃，增幅为91.7%；炕面最低温度从17.9 ℃增加到23.3 ℃，增幅为30.2%.综合考虑炕面最高温度与最低温度，本文采用275 ℃的烟气温度，此时炕面最高温度为54.1 ℃，最低温度为20.7 ℃.

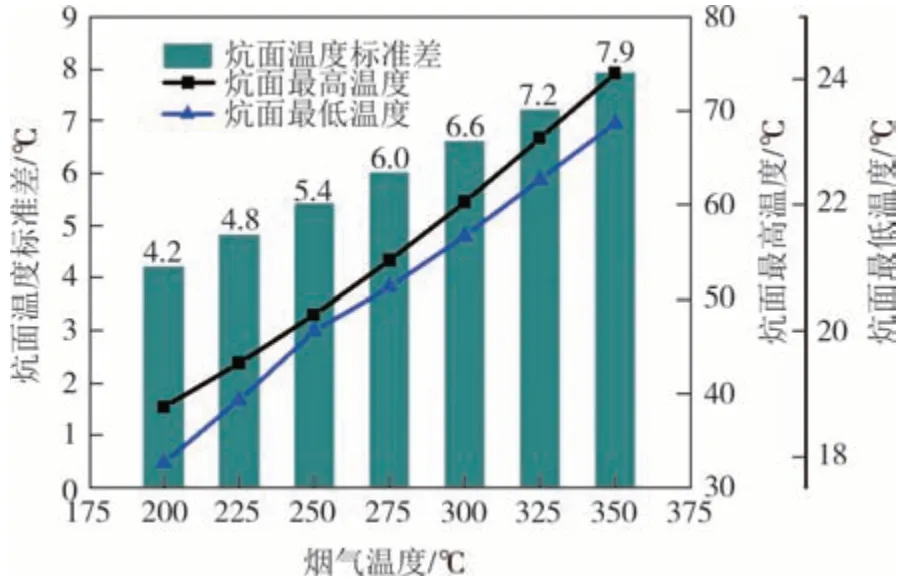
图8 入口烟气温度与炕面温度标准差、炕面最高温度、炕面最低温度的关联特性Fig.8 Influence of inlet flue gas temperature on the standard deviation，maximum temperature and minimum temperature of Kang surface

3.3 炕板蓄热层厚度与炕面温度关联特性

本文将炕头Ⅰ区的炕板蓄热层厚度增加，炕尾Ⅲ区的炕板蓄热层厚度减小.本文进行多组研究，在其中选择最具有代表性的三组数据进行说明，为60-50-40 mm（Ⅰ区炕板蓄热层厚度为60 mm，Ⅱ区炕板蓄热层厚度50 mm，Ⅲ区炕板蓄热层厚度为40 mm，简称60-50-40 mm）、70-50-30 mm（Ⅰ区炕板蓄热层厚度为70 mm，Ⅱ区炕板蓄热层厚度50 mm，Ⅲ区炕板蓄热层厚度为30 mm，简称70-50-30 mm）、80-50-20 mm（Ⅰ区炕板蓄热层厚度为80 mm，Ⅱ区炕板蓄热层厚度50 mm，Ⅲ区炕板蓄热层厚度为20 mm，简称80-50-20 mm）.

图9 为不同炕板蓄热层厚度情况下，炕面温度标准差、炕面最高温度和炕面最低温度情况.随着炕板蓄热层厚度从50-50-50 mm变化到80-50-20 mm，炕面最高温度从54.1 ℃降低到45.7 ℃，降幅为15.5%；炕面最低温度从20.7 ℃降低到17.5 ℃，降幅为15.5%；炕面温度标准差从6 ℃降低到5.8 ℃.随着炕板蓄热层厚度每次变化，炕面最高温度的变化值为1.7～4.7 ℃，炕面最低温度的变化值为0.1～2.8℃.

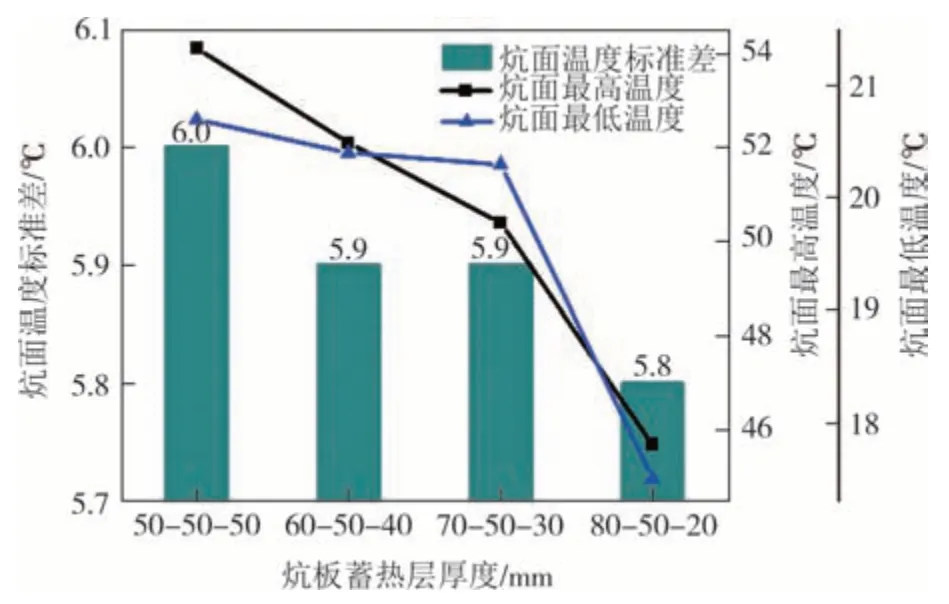
图9 炕板蓄热层厚度与炕面温度标准差、炕面最高温度、炕面最低温度的关联特性Fig.9 Influence of the thickness of the thermal storage layer on the standard deviation of Kang surface temperature，the maximum temperature of Kang surface and the minimum temperature of Kang surface

结果表明，炕板蓄热层厚度对于炕面温度标准差的影响较小，对炕面最高温度与最低温度的影响较大，本研究选择80-50-20 mm 的炕板蓄热层厚度进行后续研究.

图10 为不同炕板蓄热层厚度下的温度云图.图中表明，不同的炕板蓄热层厚度情况下，炕头温度最高.随着Ⅰ区炕板蓄热层厚度的增加与Ⅲ区炕板蓄热层厚度的减小，炕头温度明显降低，炕尾温度明显升高，炕尾高温区增大.但炕面最低温度出现于炕头，因此炕面最低温度也有所降低.

图10 不同炕板蓄热层厚度炕面温度云图Fig.10 Temperature cloud diagram of Kang surface with different thickness of thermal storage layer

3.4 烟气出入口位置与炕内烟气流动和炕面温度关联特性

根据农村居民火炕使用习惯，火炕出入口位置大致具有图11所示的4种形式，本文计算中进中出、中进侧出、侧进侧出、倒卷帘［18］四种形式并对炕面温度进行分析.

图11 烟气出入口相对位置［18］Fig.11 Relative position of inlet and outlet

图12 是四种出入口位置的炕面温度分布云图.侧进侧出形式的高温区分布在炕的一侧，而炕头位置有很大的烟气流通死角，导致炕头低温区域过大，最低温度达15.3 ℃.中进侧出形式的温度分布与中进中出形式的相差不大，炕尾的高温区偏向烟气出口一侧.倒卷帘形式的炕面温度整体更高，烟气流通死角较少，高温区集中在烟气入口的一侧，最高温度为49.8 ℃，炕头的低温区也有24.4 ℃.

图12 不同出入口位置的炕面温度云图Fig.12 Temperature cloud diagram of Kang surface at different inlet and outlet positions

图13 为不同烟气出入口位置炕面温度标准差和炕面平均温度的对比情况.倒卷帘形式的炕面温度标准差为4 种方式中最低的5.6 ℃，侧进侧出形式的炕面温度标准差是最高的7.7 ℃，两种形式炕面温度标准差相差2.1 ℃，倒卷帘形式炕面温度分布最均匀.倒卷帘形式的炕面平均温度是四种情况中最高的36.4 ℃，中进中出形式为最低的32.6 ℃，两种情况相差3.8 ℃，倒卷帘形式炕面平均温度最高.

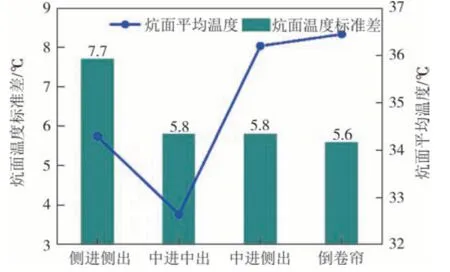
图13 烟气出入口位置与炕面温度标准差和炕面平均温度的关联特性Fig.13 Influence of flue gas inlet and outlet positions on standard deviation and average temperature of Kang surface

图14 是四种入口位置形式的炕面最高温度与炕面最低温度情况.四种形式中，倒卷帘形式炕面最高温度最高，为49.8 ℃；中进中出形式炕面最高温度最低，为45.7 ℃.倒卷帘形式炕面最低温度最高，为24.4 ℃，侧进侧出形式炕面最低温度最低，为15.3 ℃.

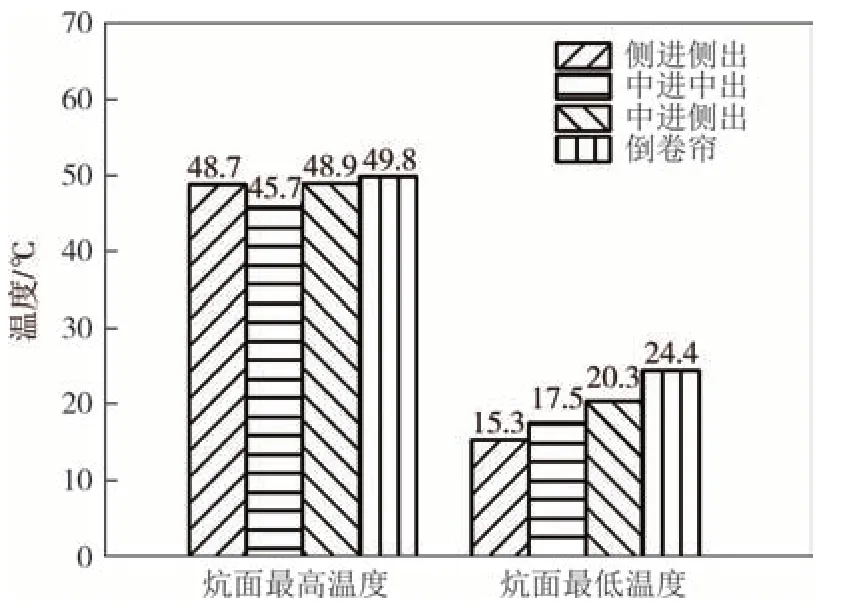
图14 不同烟气出入口位置的炕面最高温度和炕面最低温度情况Fig.14 Maximum temperature and minimum temperature of Kang surface at different inlet and outlet positions

综合上述4 种形式，倒卷帘形式具有更高的炕面最高温度、炕面最低温度和炕面平均温度，炕面温度分布也更加均匀.

4 结论

本文提出了传统火炕非均质设计方法，采用CFD 软件对中国传统火炕建立了数值模型，分析不同的关键设计参数——竖洞率、炕板蓄热层厚度、烟气温度、出入口相对位置对传统火炕上散热面温度的影响特性，得出如下结论：

1）竖洞率从0 增至33%，炕面最低温度增幅为12.1%；竖洞率从33%增至1，炕面最低温度降幅为21.2%.随着竖洞率的增大，炕面平均温度、炕面最高温度均降低，炕面平均温度降幅为19%，炕面最高温度降幅为29.4%；炕面温度标准差先减小后小幅度增加，在竖洞率为83%时达到最小值6 ℃.综合考虑选择竖洞率取83%为最佳.

2）入口烟气温度从200 ℃增加到350 ℃，炕面温度标准差、炕面最高温度和炕面最低温度均升高，炕面温度标准差介于4.2～7.9 ℃，炕面最高温度介于38.6～74 ℃，炕面最低温度介于17.9～23.3 ℃.综合考虑炕面最高温度与最低温度，本文采用275 ℃的烟气温度.

3）炕板蓄热层厚度从50-50-50 mm 变化到80-50-20 mm，炕面最高温度、炕面最低温度、炕面温度标准差均降低，炕面最高温度介于54.1～45.7 ℃，炕面最低温度介于20.7～17.5 ℃，炕面温度标准差介于6～5.8 ℃.综合考虑施工难度与炕面温度标准差，炕板厚度取80-50-20 mm为最佳.

4）火炕出入口相对位置形式采用倒卷帘时，具有最合理的炕头温度与最高的炕尾温度，炕面温度最为均匀，炕面温度标准差为最低的5.6 ℃，炕面平均温度是四种形式中最高的36.4 ℃.倒卷帘为最佳形式.

本文为传统火炕设计参数优化、节能改造提供了新思路，对传统火炕热效率提高具有参考作用.