单箱多室波形钢腹板组合箱梁约束扭转剪应力分析

黄洪猛 ，张元海 ，罗奎

（1.兰州交通大学 土木工程学院，甘肃 兰州 730070；2.西北民族大学 土木工程学院，甘肃 兰州 730030；3.湖南大学 土木工程学院，湖南 长沙 410082）

波形钢腹板组合箱梁因波形钢板正交异性、自重轻、预应力效率高、避免腹板斜裂缝等优点［1-2］，在桥梁建设中的应用越来越广泛.为适应交通量日益增长的趋势，高等级公路上的桥梁变得愈来愈宽，单箱多室波形钢腹板组合箱梁也愈受青睐.目前，已建成的单箱多室波形钢腹板组合箱梁的横截面有单箱双室、单箱三室、单箱四室、单箱五室、单箱七室等.

与传统混凝土箱梁相比，受波形钢腹板的褶皱效应的影响，波形钢腹板组合箱梁的扭转和畸变效应变得更加突出.在工程实践中，一般将偏心荷载作用下箱梁产生的扭转和畸变单独分析.邓文琴等［3］分析了单箱三室波形钢腹板悬臂梁的扭转与畸变效应，指出约束扭转主要产生翘曲剪应力，畸变主要产生翘曲正应力，但没有具体分析翘曲剪应力对约束扭转翘曲剪应力的影响.马磊等［4］推导了单箱双室波形钢腹板组合箱梁扭转与畸变控制微分方程，但仅分析了翘曲正应力，未分析剪应力.Shen 等［5］、Zhu等［6］对单箱多室波形钢腹板箱梁的纯扭转性能进行了试验和理论研究，分析了扭矩-扭率关系及自由扭转剪应力的分布.在实际工程结构中，箱梁的扭转问题几乎都表现为约束扭转［7］，而偏心荷载作用在横截面内产生的扭转剪应力是混凝土顶底板抗裂验算和波形钢腹板抗剪验算的重要内容，且波形钢腹板的抗剪性能成为限制桥梁跨径的主要因素［8］.因此，分析单箱多室波形钢腹板组合箱梁的约束扭转剪应力及其对波形钢腹板抗剪性能的影响具有重要的意义.乔朋等［9］利用有限元模拟研究了单箱多室波形钢腹板组合箱梁各腹板剪应力的分布规律，指出偏心荷载下腹板弯扭剪应力不均匀分布系数超过4.5.Li等［10］对主梁为单箱四室波形钢腹板组合箱梁的斜拉桥进行荷载试验和有限元分析，结果表明对称荷载或偏心荷载下各腹板的剪力分布不均，且混凝土顶底板可分担一定的剪力.已有文献对波形钢腹板组合箱梁的约束扭转分析主要是基于乌曼斯基第二理论，而乌曼斯基第二理论应用了剪应力的两种算式，出现了两种不一致的纵向翘曲位移［11］.张元海等［12］指出约束扭转剪应力应按微元体平衡条件或根据自由扭矩和翘曲约束扭矩进行计算，不能直接按胡克定律计算.徐勋等［13］基于广义坐标法和混合变分原理建立了薄壁箱梁约束扭转分析新理论，与Reissner 原理的结果是统一的，均考虑了全部次生剪应力对中面剪切变形的影响，计算精度更高.鲍永方等［14］对约束扭转分析的乌曼斯基理论和Reissner 原理进行比较，指出Reissner原理的计算精度高于乌曼斯基理论.

目前对单箱多室波形钢腹板组合箱梁约束扭转剪应力的分析不够全面，而且相关规范对波形钢腹板设计时也仅考虑了自由扭转剪应力.本文为合理计算单箱多室波形钢腹板组合箱梁的约束扭转剪应力，对剪力流进行分解，根据剪力流的传递路径、微元体纵向平衡及翘曲位移连续性，引入能够反映各室箱壁剪力流传递规律的常数，推演出截面几何特性和剪应力实用计算公式.波形钢腹板剪切刚度小，剪切变形大，需考虑全部次生剪应力对剪切变形的影响，故将位移和应力同时作为变分参量，基于Reissner 原理建立能量泛函并推导波形钢腹板组合箱梁约束扭转控制微分方程，采用初参数法求得其解析解.以单箱多室波形钢腹板简支箱梁为算例，详细分析了梁宽和箱室数量等参数变化对剪应力的影响，为同类型桥梁的设计提供参考.

1 截面应力及几何特性的计算公式

波形钢腹板组合箱梁因各板件材料不同，约束扭转分析时需通过等效方法将材料统一.根据波形钢腹板的力学性能先将其等效为正交异性平钢板，再等效为混凝土腹板，由于波形腹板主要承受剪力，可采用剪切模量比计算波形钢腹板等效为混凝土腹板的厚度.另外，波形钢腹板在纵向表现出明显的褶皱效应，采用卡氏第二定理及位移等效方法，可求得波形钢腹板等效为混凝土腹板后的纵向等效弹性模量.

1.1 自由扭转剪应力及抗扭惯性矩

图1 所示为单箱多室波形钢腹板组合箱梁横截面：O为扭转中心，y轴为过扭转中心的水平轴，z轴为竖向对称轴，bf、b、bi分别为悬臂板宽度、闭合箱室总宽度和i室的宽度，h为梁高，tt、tb分别为顶板、底板的厚度.

根据刚性周边假设，自由扭转时多室箱梁的各室具有相同的扭率φ′.由单室箱梁环流方程∮(qs/t)ds=Gcφ′Ω，考虑共用腹板上的剪力流为本室与相邻室剪力流的叠加，则i室剪力流与扭率φ′之间的关系为

波形钢腹板等效为混凝土腹板后的等效厚度twe，可采用等效剪切模量比求得，表达为

式中：aw、bw、cw、tw分别为波形钢腹板的直板长、折板水平投影长、折板长、板厚；Gse为波形钢腹板的等效剪切模量［15］；Gs为钢板的剪切模量.

对于i室，引入扭转常数ψi，令qs，i=Gcφ′ψi，并将其代入式（1），可得

借助式（3）按不同箱室分别列方程，联立方程可求得扭转常数ψi.

根据内外力系的平衡关系，各室剪力流合成的扭矩之和为闭合箱室分担的自由扭转扭矩Msc.总自由扭转扭矩Ms包含悬臂板分担的自由扭转扭矩Mso和闭合箱室分担的自由扭转扭矩Msc，即

引入扭转常数后，将抗扭惯性矩Id表达为仅与截面几何参数有关的公式，而传统方法中没有准确建立Id的表达式，且求解过程相对复杂.

将式（4）代入qs，i=Gcφ′ψi，假设剪应力沿壁厚均匀分布，得i室闭合箱壁上的自由扭转剪应力τsi为

文献［3］中单箱多室波形钢腹板组合箱梁自由扭转剪应力按照τs=Ms/(Ωt)计算，使得自由扭转剪应力在闭合箱壁顶底板宽度上均匀分布，且内腹板上无剪应力，这与实际不符.

1.2 翘曲正应力与广义主扇性惯性矩

分析箱梁约束扭转时，需考虑翘曲剪切变形影响，引入广义翘曲位移β′(x).壁厚中面上任一点的纵向翘曲位移u(x，s)和切向位移v(x，s)分别为

式中：β′(x)为广义翘曲位移；ρ(s)为扭转中心至各板壁厚中面的垂直距离；ωˉ(s)为壁厚中面任一点广义主扇性坐标，根据剪力流传递规律，其表达为

由式（6）可得壁厚中面任一点的应变表达式为

由刚性周边假设得εs=0，将式（7a）代入平面问题的物理方程，得翘曲正应力σω为

采用卡氏第二定理及位移等效方法，可求得波形钢腹板等效为混凝土腹板后的纵向等效弹性模量，进而得到λ的表达式为

式中：hw为波形钢腹板的波高，Es为钢板的弹性模量.

1.3 翘曲剪应力与广义扇性静矩

考虑剪应力沿壁厚为均匀分布，联立式（10）和式（11），得A点处翘曲剪应力τωA为

式中：Mω为翘曲约束扭矩，Mω=Bω′.

计算悬臂板时，将s坐标原点取在悬臂板自由端，当计算的翘曲剪力流方向与s方向一致时为正，反之为负.若由式（11）计算的左侧悬臂板翘曲剪力流为正值，则翘曲剪力流指向悬臂板根部.对具有竖向对称轴的箱梁，根据广义主扇性坐标的反对称性及坐标s的方向，左、右两侧悬臂板上的翘曲剪力流也表现为反对称性，即从一侧悬臂板根部流入的翘曲剪力流必从另一侧悬臂板根部流出［7］.

按剪力流传递路径最短的原则，如图2 所示，左侧悬臂板根部F点的翘曲剪力流qωF只流经顶板，且在闭合箱壁重分布后引起翘曲剪力流qω1，qω1在各室均满足翘曲位移连续性条件∮(qω1/t)ds=0.对于i室，则有

借助式（14）按不同箱室分别列方程，联立方程可得qω1，i，并将其简化为

式中：Ki为qωF流经顶板时在i室重分布的系数.

闭合箱壁横截面上的翘曲正应力在闭合箱壁上会引起翘曲剪力流qω2.求解该部分剪力流时先在每室虚构一个切口，然后根据微元体纵向平衡条件及式（8）求得i室箱壁的翘曲剪力流qω2，i为

借助式（17）按不同箱室分别列方程，联立方程可得qω20，i，从而求得翘曲剪力流qω2，i为

式中：Li为i室闭合箱壁上翘曲正应力引起的翘曲剪力流修正常数.

将悬臂板根部流入顶板的翘曲剪力流qωF与闭合箱壁上翘曲剪力流qω1，i、qω2，i叠加，可得闭合箱壁横截面上翘曲剪应力τωi为

2 基于Reissner原理建立控制微分方程

基于Reissner 原理建立波形钢腹板组合箱梁约束扭转控制微分方程时，将位移和应力都作为变分参量，建立的能量泛函如下：

式中：σ为应力向量；ε(u)为应变向量；V*(σ)为余能密度；F为体力向量；P为面力向量；u为位移向量；l为跨径；V为体积；x为纵轴.

将式（5）、式（7）、式（10）和式（19）代入式（20）右侧第1项，得

式中：τz为总扭转剪应力，τz=τs+τω；Mz为总扭矩，Mz=Ms+Mω.

将式（5）、式（10）和式（19）代入式（20）右侧第2项，得

当箱梁上仅作用分布扭矩mt时，外力势能为

将式（21）～式（23）代入式（20），并对能量泛函∏进行一阶变分运算，可得

由δ∏=0，可得能量泛函的约束条件：

力与位移的关系条件

力的平衡条件

联立式（25）和式（26），经整理，得约束扭转控制微分方程为

式（27）微分方程可采用初参数法求解［16］.对跨中截面作用集中扭矩荷载T的简支箱梁，其广义位移和广义内力的解析表达式分别为

推导约束扭转控制微分方程时采用了刚性周边假设，未考虑横隔板设置对约束扭转效应的影响.横隔板的设置主要是为了避免箱梁截面发生畸变变形，从而使刚性周边假设成立.Reissner 原理将位移和应力都作为变分参量建立能量泛函，余能函数中含有剪应力的平方项，亦计入所有剪应力所做的功，即考虑了全部次生剪应力对剪切变形的影响，因此该理论更准确.

3 数值算例分析

3.1 算例概况

参照大广高速公路卫河大桥，选取计算跨径l=52 m 的等截面单箱三室波形钢腹板简支箱梁为分析算例.梁端设置1.0 m 厚横梁，跨内布置3 道0.2 m厚横隔板；在跨中截面左侧两腹板与顶板交接处作用偏心竖向集中荷载P=360 kN，该荷载可分解为对称和反对称竖向荷载，反对称荷载产生的扭矩为2 745 kN·m，本文仅研究扭矩产生的约束扭转剪应力，未考虑反对称竖向荷载产生的畸变效应；波形钢腹板采用1 200 型，aw=330 mm，dw=336 mm，hw=200 mm，tw=12 mm；顶底板及横隔板采用C50 混凝土，其弹性模量Ec=34.5 GPa，剪切模量Gc=13.8 GPa，泊松比μc=0.2；波形钢腹板采用Q345钢，其弹性模量Es=206 GPa，剪切模量Gs=79 GPa.组合箱梁横截面尺寸如图3 所示，图中还示出了计算点Ⅰ～Ⅳ和WA～WD的位置.

3.2 理论验证及剪应力分析

现有的扭转和畸变试验中，通常将扭转和畸变耦联在一起，很难将扭转或畸变结果独立出来［17］，因此本文采用ANSYS 空间有限元结果来验证所提解析方法的正确性.为避免有限元模型中跨中横隔板和集中扭矩施加位置的局部影响，采用ANSYS 有限元法和解析法计算了距跨中2.7 m 左侧横截面计算点的总扭转剪应力τz，计算结果列于表1 中.表1 中的相对误差为解析解与ANSYS 解的差除以ANSYS解得到的.采用ANSYS 有限元数值模拟计算时，混凝土板件和波形钢腹板分别采用SOLID45 实体单元和SHELL63壳单元模拟，全梁共划分为167 024个实体单元，26 240 个壳单元和263 245 个节点，壳单元和实体单元间用主从约束作刚性连接处理，有限元模型如图4 所示.有限元模型中，将偏心竖向荷载产生的扭矩按自由扭转剪力流的计算方法等效成沿壁厚均匀分布的剪力流，均匀施加于跨中截面闭合箱壁各单元的节点上，该荷载仅产生约束扭转效应而不产生畸变.由表1可以看出，解析解与ANSYS 解的相对误差在±10%以内，即本文所提方法的解析解与ANSYS空间有限元解吻合良好.

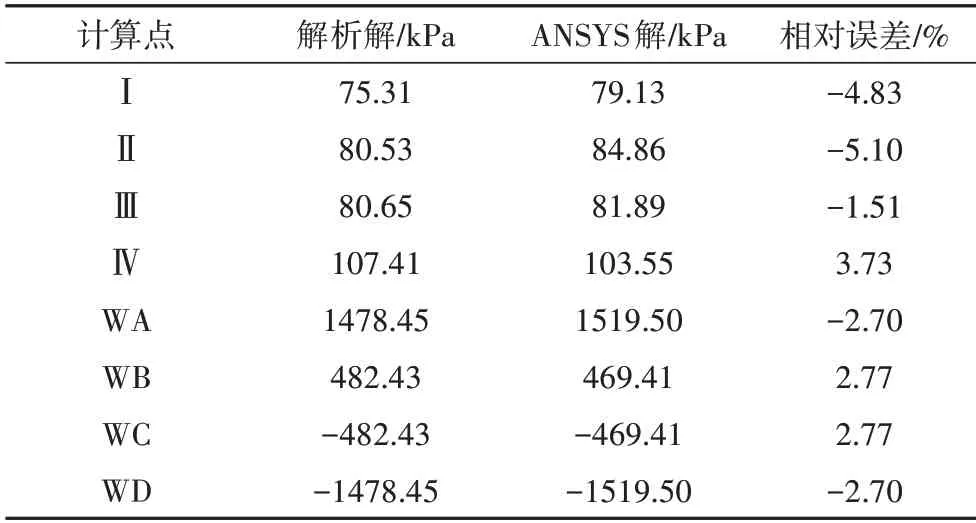
表1 距跨中2.7 m处左截面的总扭转剪应力对比Tab.1 Comparison of total torsional shear stress at left section 2.7 m from mid-span

图4 组合箱梁有限元模型Fig.4 Finite element model of composite box girders

借助所建立的剪应力公式计算了扭矩荷载下组合箱梁跨中截面各计算点的自由扭转剪应力τs、翘曲剪应力τω和总扭转剪应力τz，计算结果列于表2中.为分析扭转剪应力对腹板总剪应力的影响，表2中还给出了对称竖向荷载下的弯曲剪应力τM.弯曲剪应力沿腹板高度均匀分布［18］，且认为其全部由腹板均匀分担.由表2 可以看出：1）混凝土顶底板上出现了可观的扭转剪应力，尤其是混凝土底板上的扭转剪应力，其影响主拉应力的大小和分布，应予以重视；2）顶底板上内、外室的自由扭转剪应力不相等，内室（Ⅱ和Ⅳ点处）与外室（Ⅰ和Ⅲ点处）的比值为1.28，因此单箱多室波形钢腹板组合箱梁的自由扭转剪应力不能按照单箱单室简化计算；3）顶板Ⅱ点和内腹板WB 点处的自由扭转剪应力分别为总扭转剪应力的1.37 和0.80 倍，亦即翘曲剪应力与自由扭转剪应力叠加后使得Ⅰ点总扭转剪应力减小37%，WB 点总扭转剪应力增大20%，因此，约束扭转分析时翘曲剪应力不可忽略；4）外腹板WA 点处扭转剪应力与弯曲剪应力叠加后的总剪应力值为弯曲剪应力的1.52 倍，且腹板间的剪应力在偏心竖向荷载下表现出明显的分布不均匀性.

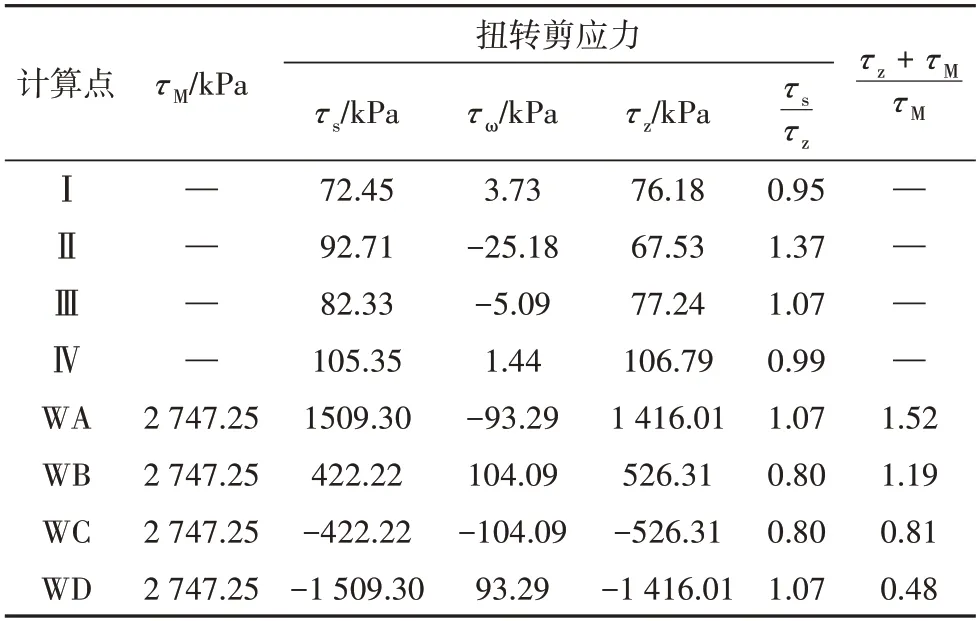
表2 跨中截面各计算点的剪应力解析解Tab.2 Analytical solution of shear stress of calculation point at mid-span section

为了对比单箱多室波箱钢腹板组合箱梁与传统混凝土箱梁约束扭转剪应力的分布差异，将图3 中波形钢腹板调整为25 cm厚的混凝土腹板.采用解析法计算了单箱多室混凝土箱梁各计算点的剪应力，计算结果如表3 所列.由表3 可以看出：与波形钢腹板组合箱梁比较，单箱多室混凝土箱梁顶底板自由扭转剪应力较小，但翘曲剪应力的占比较大，尤其是在混凝土腹板上，翘曲剪应力大于自由扭转剪应力，且两者的传递方向相同.而波形钢腹板上的翘曲剪应力虽对实际扭转剪应力有一定的影响，但小于自由扭转剪应力，且翘曲剪应力和自由扭转剪应力的传递方向不一定相同，这是因为波形钢腹板的褶皱效应影响着截面几何特性和扭转剪应力的传递规律.

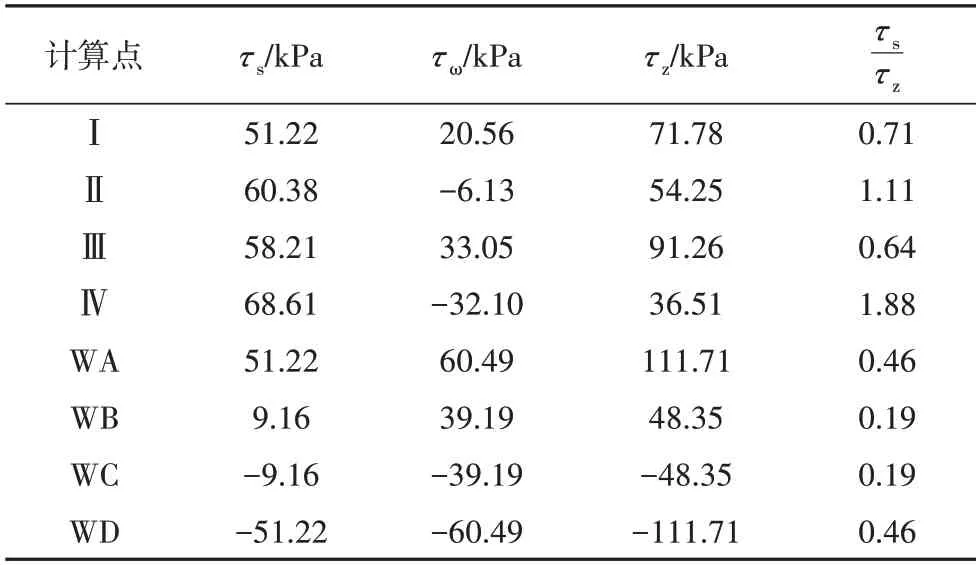
表3 混凝土箱梁跨中截面的扭转剪应力解析解Tab.3 Analytical solution of torsional shear stress at midspan section of concrete box girder

3.3 参数影响分析

为了考察翘曲剪应力在总扭转剪应力中的贡献和腹板上总扭转剪应力对考虑弯曲剪应力后的总剪应力的影响，引入剪应力系数η和剪应力增大系数ζ.剪应力系数η为自由扭转剪应力与总扭转剪应力的比值，剪应力增大系数ζ为总扭转剪应力与弯曲剪应力叠加后的总剪应力与弯曲剪应力的比值.

单箱多室波形钢腹板组合箱梁的箱室数量是为了适应梁宽的受力要求进行设置的，而梁宽决定着截面几何特性，进而影响约束扭转剪应力.箱梁上作用的扭矩值不变，调整图3 组合箱梁横截面使各箱室等宽，并改变闭合箱室总宽b，使其从7.8 m以0.78 m为步长增至15.6 m，用解析法得到的总扭转剪应力τz、剪应力系数η、剪应力增大系数ζ随梁宽变化曲线如图5 所示.从图5 可以看出：随着梁宽的增大，顶、底板和腹板的扭转剪应力均减小，另外，梁宽较小时，底板上的扭转剪应力比较突出；外腹板的剪应力增大系数最大为1.57，随着梁宽的增大，腹板的剪应力增大系数虽减小，但减小幅度很小，外腹板的剪应力增大系数由1.57 减小至1.44，内腹板的由1.19 减小至1.16，可见，箱梁上作用的扭矩值保持不变时，腹板的剪应力增大系数对梁宽的变化不敏感，且偏心竖向荷载作用下内外腹板间的剪应力分布不均匀；翘曲剪应力对约束扭转剪应力的影响不可忽略，顶板Ⅱ点和外腹板的剪应力系数最大分别达到1.40、1.32，内腹板的剪应力系数最小为0.65，即顶板Ⅱ点和外腹板的翘曲剪应力在总扭转剪应力的占比分别达到-40%和-32%，内腹板的占比达到35%.

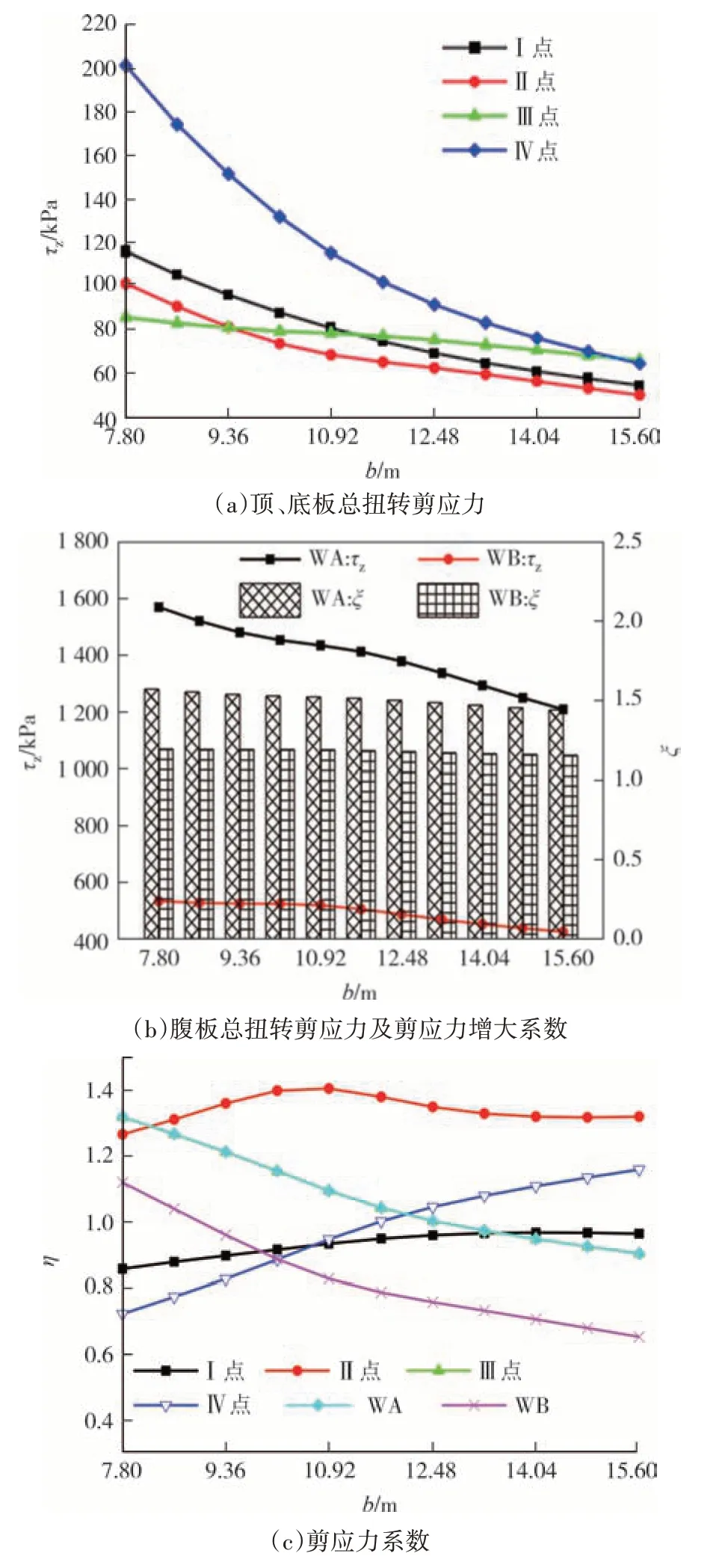
图5 梁宽对单箱三室组合箱梁剪应力的影响Fig.5 Effect of girder width on shear stress of single-box three-cell composite box girders

以闭合箱室总宽b的变化为基准，调整箱室数量为竖向对称双室、三室、四室，图6 绘出了不同箱室组合箱梁的总扭转剪应力τz、剪应力系数η和剪应力增大系数ζ随梁宽的变化曲线.从图6 可以看出：随着梁宽的增大，不同箱室组合箱梁的扭转剪应力均减小，且箱室越多，扭转剪应力越小，当梁宽b=15.60 m 时，与单箱双室箱梁比较，单箱三室、四室箱梁顶板Ⅰ点处分别减小14.9%、31.2%，外腹板的扭转剪应力分别减小12.3%、27.4%；箱梁上作用的扭矩值保持不变，随着梁宽的增大，不同箱室组合箱梁外腹板的剪应力增大系数均减小，单箱双室、三室、四室箱梁外腹板的剪应力增大系数分别由1.49、1.57、1.69 减小至1.38、1.44、1.45，且箱室越多，剪应力增大系数越大；随着梁宽的增大，顶板Ⅰ点处的剪应力系数增大，而外腹板的剪应力系数减小，顶板Ⅰ点处的剪应力系数最小为0.82（单箱双室箱梁），外腹板的剪应力系数最大为1.32（单箱三室箱梁）.

图6 不同箱室组合箱梁的剪应力随梁宽的变化Fig.6 Variation of shear stress of different cell numbers box girders with girder width

4 结论

本文将位移和应力同时作为变分参量，基于Reissner 原理推导出波形钢腹板组合箱梁的约束扭转控制微分方程，并采用解析理论对单箱多室波形钢腹板组合箱梁的约束扭转剪应力及其随截面几何参数变化规律进行了分析，结论如下：

1）对剪力流进行分解，根据剪力流的传递路径、微元体纵向平衡和翘曲位移连续性条件，引入能够反映各室箱壁剪力流传递规律的常数，推导出了截面几何特性和剪应力实用计算公式，计算公式物理意义明确，计算简便不易出错.数值算例的ANSYS空间有限元解验证了本文解析法的正确性.

2）数值算例的参数影响分析表明，当箱梁上作用的扭矩值不变时，梁宽增大和箱室增加均能有效减小约束扭转剪应力.在对波形钢腹板组合箱梁设计时，应充分考虑翘曲剪应力对总扭转剪应力的影响，以及扭转剪应力对顶底板主拉应力的影响，避免主拉应力超限引起混凝土斜裂缝.

3）在偏心竖向荷载作用下，约束扭转剪应力使得腹板间的总剪应力分布明显不均匀，且当竖向荷载不变时，箱室越多分布不均匀性越明显.在对该类型桥梁设计时，应充分考虑偏心荷载作用下腹板的剪应力增大系数.