双向人群流疏导的人行桥减振控制研究
朱前坤 ,卫晓妮 ,杜永峰 ,2
(1.兰州理工大学 防灾减灾研究所,甘肃 兰州 730050;2.兰州理工大学 西部土木工程防灾减灾教育部工程研究中心,甘肃 兰州 730050)
近年来随着我国经济的快速发展,轻质、高强的大跨度结构开始大量涌现于建筑市场,此类结构通常具有低频率、低阻尼的特点,易与人行荷载的频率接近发生结构的共振现象,严重时可能引发安全事故[1-2].
自2000 年伦敦千禧桥发生人致振动事件而被迫关闭之后,大量学者针对人致振动问题展开了深入而广泛的研究[3].我国在《城市人行天桥与人行地道技术规范》(CJJ 69—1995)[4]中规定人行桥一阶竖向自振频率不得小于3 Hz 来避免产生人桥共振现象.这样的规定仅能作为设计阶段的初步预测,在实际工程中采用调谐质量阻尼器(TMD)减振技术是一种经济、实用的方法,可对结构起到良好的控制作用.除了作用于结构本身之外,改变激励源也是一种广泛应用的方法.基于激励源的减振策略已经在高层建筑和大跨桥梁上有所应用,Kareem 等[5]通过改变高层建筑的螺旋桨重新塑造整体结构来减少风引起的振动.Sarwar 等[6]通过引入其他元素,比如在桥面周围添加导叶来减少风引起的大跨桥梁的振动.在解决行人引起的人行桥过量振动问题时,可以通过控制人群流量来获得基于激励源的减振方法.在人行桥设计时,出于安全考虑会布置路灯、长椅以及护栏等部件,通过优化以上部件的位置可以对行人流量进行控制达到扰乱行人步行频率以减少人行桥振动的目的.Carroll等[7]首先提出了利用离散元方法(DET)来建立人群模型,并以时间步长为框架,将离散元群体模型与动态桥梁模型耦合在一起,实现人群-桥梁的相互作用.Venuti 等[8]利用MassMotion 软件模拟人群流,通过在人行桥上设置障碍物,控制人群流量来缓解人群引起的竖向振动,并与最优设计的TMD 进行减振效果的比对.以上人群模拟的方法都具有一定的局限性,由Helbing 等[9]在1995 年提出的社会力模型因将行人运动描述为各项物理力的总和,能够非常逼真地描述行人群的自组织行为而得到了广泛地应用.单庆超等[10]、李珊珊等[11]、李昌华等[12]对社会力模型中各个参数、运动方向的选择进行改进,引入行人减速避让机制来避免行人发生碰撞,解决了行人运动轨迹单一、人群松散、与实际运动不符等问题.Zhu 等[13-14]利用考虑行人自停和减速避让机制的改进社会力模型模拟人群流并与结构进行耦合研究结构的振动舒适度问题,通过合理地布置障碍物,打乱行人步频使施加于结构的动荷载发生变化来控制结构的过量振动.
但以上研究仅仅针对单向行人流,在实际的交通中,人群运动往往会以双向人群流的方式出现,因此,本文在前人的研究基础上,提出了一种通过布置障碍物进行双向人群流的疏导来控制结构振动的方法,研究布置障碍物对行人施加于结构上的步行力、步行特性的改变以及对结构振动响应的影响,最终从能量的角度解释了人行桥减振的机理.
1 改进的社会力模型
1.1 基本原理
Helbing 等提出的社会力模型中行人运动是由行人个体的行为以及周围环境的影响共同完成的,包括3 个基本力:自驱动力、行人间相互作用力以及行人与周围障碍物作用力,这些力的合力作用于行人,产生一个加速度达到最终的目的地,模型一般形式的表达式如下式所示:
式中:每一个行人i的质量是mi,vi是步行速度.
2)行人间的作用力fij:是行人在移动过程中希望与其他行人保持一定距离的意愿,当行人间距离压缩到一定范围时,双方均有一种意愿试图增加这个距离,这种意愿由社会心理力和身体接触力组成.
式中:A和B为固定系数,分别代表作用力强度和作用力范围;dij(t)=‖xi(t)-xj(t)‖是两个行人中心间的距离;rij=ri+rj是两个行人间的半径之和;正常情况下,功能函数Θ(ϕij)反映行人i与其周围行人j产生的相互作用力当中,位于i前方的行人产生主要作用,后方行人产生的作用力可忽略不计,Helbing等[15]将其表示为:
式中:λi为各向异性参数,考虑了不同方向的行人对当前行人的不同影响程度,一般认为前方行人影响大于后方行人,λi越小表示前方行人影响越大,λi∈[0,1];nij(t)=[ri(t) -rj(t)]/dij(t)是行人j指向行人i的单位化矢量,关系示意图如图1.
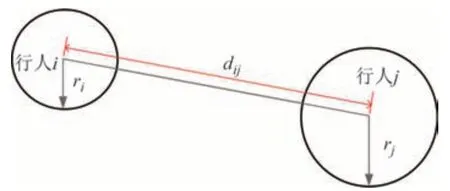
图1 行人之间距离示意图Fig.1 The distance between two pedestrian
只有当两行人之间有身体接触后才会产生身体接触力,即两行人之间的半径之和大于中心之间的距离时,由身体相互接触的压力和滑动摩擦力组成,表达式如下:
式中:K为人体弹性系数(N•m-1),k为人体相对速度差摩擦系数(N•s•m-2);nij表示行人j指向行人i的单位向量;tij表示切线方向;Δvij=(vj-vi)∙tij表示两个行人在切线方向的速率差.
3)行人与周围环境(如障碍物)之间的作用力fiw:与行人之间的作用力fij类似,表示为:
式中:Aw是行人与障碍物作用力强度;Bw是行人与障碍物作用范围;riw-diw是行人半径与行人到障碍物的法向距离差;niw是障碍物指向行人的单位法向量;是行人速度在障碍物方向上的投影.
在双向行人相互作用中,我们需要考虑逆向行人的避让和碰撞行为.根据实际经验,当行人运动时,行人有相应的视野范围,行人会根据视野内的其他物体和环境情况来做出反应.张海均等[16]引入“行人感知域”S来区分出现在感知域内和不出现在感知域内的两类行人,只计算出现在感知域内的行人产生的相互作用力.此外,避免行人碰撞在行人仿真中具有重要地位,避免发生碰撞行为是行人的主观意识,这种力应该由行人自身发出.在本文的模拟中,取感知区域长度L=5 m,扇形角度采用124°的行人视角,如图2 所示.逆向行人进入当前行人的感知域后,当前行人的心理排斥力f′socij会进行修正,同时受到避让力f′avoi的作用进行减速[17],修正后的表达式如下:

图2 行人受力示意图Fig.2 The force on pedestrian
式中:Sij=Leθ,L=5m,θ=124°.
其中:-δi(t)vi(t)代表行人i在δi(t)时间内速度从vi(t)减少到0时产生的加速度值.
以上社会力模型仅能应用于畅通的空间场景,对于有障碍物的复杂空间场景,当行人目标点受到障碍物的遮挡限制时,社会力模型将无法产生合理的运动轨迹,行人会受到阻碍陷入困境,无法前进.根据实际经验,当障碍物遮挡时行人会选择绕行,在社会力的驱使下行人绕行行为通过坐标发生变化实现.当行人与障碍物的距离超过障碍物影响范围内的心理安全距离(0.3 m)时,社会力使行人在障碍物周围恢复初始速度继续朝着目的地前进.
1.2 行人流仿真模拟
选用某长度L=22 m,宽度W=3 m 的通道为研究对象进行双向行人流仿真模拟,为了与单向模拟结果形成对比,在每种工况行人密度保持一致的情况下左右行人数量也保持一致.行人数量变化范围为10~70,按10人的差值依次递增,每种工况模拟30组并计算平均值,以保证结果的准确性.假设右行行人的最终目的地是通道最右侧边缘,行人在坐标轴0处的左侧虚拟空间随机生成,自坐标轴0 处进入通道,在力的作用下向目的地移动,直到从右侧通道口走出.同理,左行行人在坐标轴22 m 的右侧虚拟空间随机生成,自坐标轴22 m 处进入通道向最终目的地左侧边缘移动,直到从左侧通道口走出,完成循环.
模拟结果如图3 所示,行人平均步行速度随着行人数量的增加而降低,呈负相关.将单、双向进行对比可知在行人密度低于0.9 人/m2时,双向行人平均步行速度整体是低于单向的,这是行人之间的相互作用所致.随着行人密度的增加,双向人群中行人平均步速比单向人群下降幅度更小,导致两个人群之间的差异逐渐变小,甚至出现双向超过单向的现象.这是由于在双向人群模拟中,行人之间的作用力大小、方向都更为复杂,行人速度对行人密度更加敏感.结合以上的结论可知,对双向人群流展开相关的研究是十分必要与重要的.
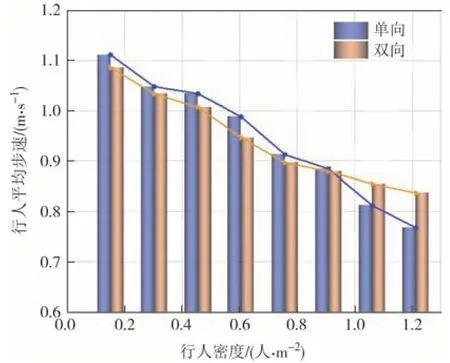
图3 行人密度-平均步速关系图Fig.3 Pedestrian density-velocity relationship15
2 结构振动响应计算
2.1 耦合系统的建立
在人行桥设计中,许多规范将行人步行力视为确定性移动荷载[18],忽略了行人对人-结构系统动态特性的影响以及结构振动对行人的影响.如果不考虑这部分人-结构的相互作用,在对结构振动舒适度进行评估时就会高估结构的振动响应,近年来对人-结构相互作用的研究主要参考Venuti等[19]提出的行人是包含质量、阻尼和刚度的MSD模型.将每个行人各个位置的MSD 模型应用于结构,结构被视为是一个一维简支梁,结构动力响应以竖向振动为主,耦合模型的示意图如图4所示.
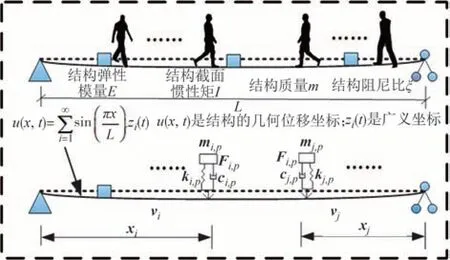
图4 人群-结构耦合模型示意图Fig.4 Crowd-structure coupling model
结构与人体的耦合系统由人体动力系统和结构动力系统两部分组成.本文沿用课题组之前的研究[13]建立耦合系统的振动控制方程.引入Bertram 和Ruina[20]研究提出的行人步行频率和速度之间的关系式:
式中:fp是行人的行走频率,将行人质量G和步频fp代入傅里叶级数形式的荷载模型中,如下所示:
式中:N为当前结构上的行人数;αi是动载系数;φi是行人的相位角,取值参考朱前坤等[21]的研究结果.
在人行桥的模态振动分析中仅考虑一阶模态对结构振动的影响.若进入结构的行人数量为H,则系统有H+1个自由度,动态耦合模型的矩阵表示如下:
其中,M、C、K分别为耦合系统的模态质量、阻尼和刚度,一阶振型函数ϕ1(x)=sin是某一时刻t人行桥上行人数量是N时的外部步行荷载,y是位移的广义向量.随着两侧行人不断进入系统,耦合系统发生时变,当行人进入系统时,耦合系统的自由度增加,M、C、K、F、y随之扩大一个自由度.将上述二阶微分方程用MATLAB 进行编程求解,采用Newmarkβ法求解结构响应.
2.2 案例研究
选用某商贸城的一个钢结构连廊在MATLAB 平台上进行仿真模拟,该连廊结构跨度L=21.8 m,宽度为W=3 m,结构的阻尼比ξ=0.01.截面竖向等效抗弯刚度为EI=3.268×109N·m,单位长度质量为1 063.5 kg/m,阻尼系数C=950.8 N/(m·s-1),结构的一阶频率为5.79 Hz.
计算结果如图5所示,随着行人密度的逐渐增加,结构加速度峰值依次增加.行人密度低于0.6人/m2时,相同密度下单向行人作用于结构产生的结构加速度响应高于双向行人.当行人密度超过0.6 人/m2时,双向行人流作用于结构产生的结构加速度响应大于单向且随着人群密度的增加差值增大.双向人群密度为1.212 人/m2时,结构加速度响应峰值高达1.602 m/s2,远远超过了《建筑楼盖结构振动舒适度技术标准》(JGJ/T 441―2019)中规定的不封闭连廊竖向峰值加速度限值0.5 m/s2,使行人产生强烈的不适感.因此,当行人密度过高时,结构响应会引起行人的恐慌,有必要对双向人群流展开相关研究并通过控制人流进行结构的减振控制.
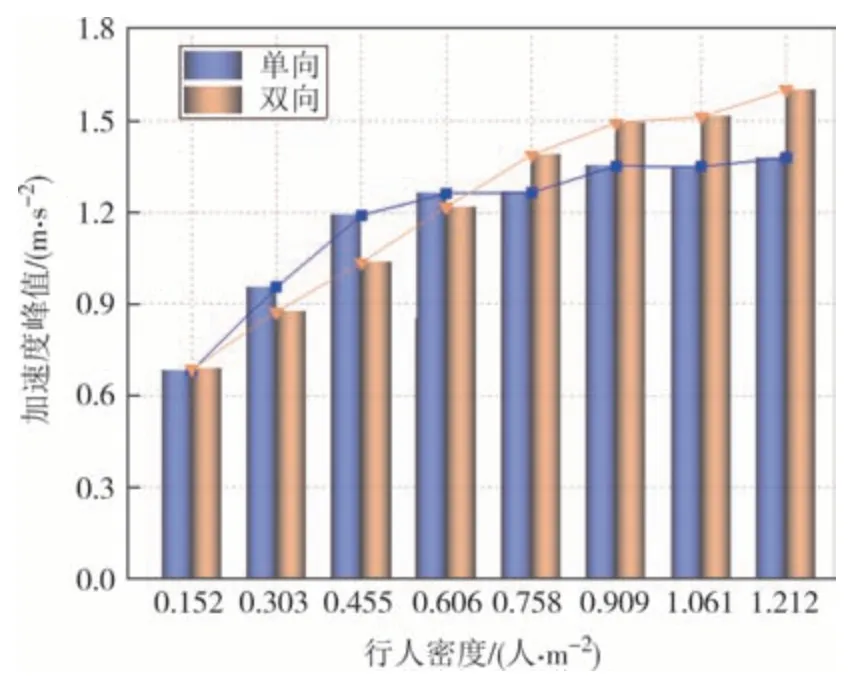
图5 不同行人密度下的结构加速度峰值Fig.5 Peak structure acceleration under different pedestrian density
3 双向人群流减振策略的验证
结合上一节,双向人群密度在0.6人/m2时引起的结构加速度响应已经过大,引起行人强烈的不适感,通过疏散人群流的方式来降低结构的竖向振动是最简单实用的方式.在实际生活中,连廊上的路灯、长椅、护栏等永久性设施除了发挥其实用性作用之外,必要时刻还可以用来进行人群流的疏散与引导.我们可以通过合理地布设其摆放位置,打乱行人行走的轨迹,扰乱行人步行频率,使行走特性趋于不同,改变施加于结构上的动荷载,以降低结构动力响应.
3.1 实验过程
利用实验室人行桥来验证双向人群流的减振策略.实验室人行桥长10 m,宽1.6 m,在无外荷载的情况下,人行桥的频率在4.3 Hz左右.
实验中,保证双向行人数量相同,各1 个行人、2个行人分别在无障碍物和设置4 个障碍物的工况下对向行走进行对比实验,每组工况分别进行5 组实验.选取的实验对象为在校研究生,保证质量均为65 kg 左右,加速度传感器(941B)和信号采集(DASP)分析仪(INV3060V)装置用于采集和获取结构振动响应.为了保证结果的精度,有必要将加速度传感器粘贴在人行桥的中间位置,该位置由一阶振型控制.实验场景如图6所示.
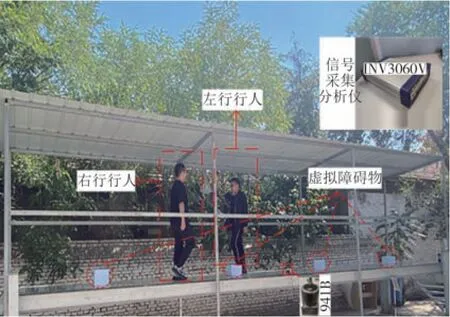
图6 加速度采集试验现场图Fig.6 The experimental scene
3.2 实验结果分析
图7(a)和7(b)分别为双向各1 个行人的加速度时程图和对应的傅里叶谱,设置4 个障碍物后峰值加速度从0.165 m/s2减小到0.144 m/s2,傅里叶幅值从0.020 m/s2减小到0.012 5 m/s2.同样地,对于双向各2个行人的工况结果如图8 所示,设置障碍物后峰值加速度从0.218 m/s2减小到0.189 m/s2,傅里叶幅值从0.021 m/s2减小到0.016 m/s2.以上两种工况表明设置障碍物能有效地降低结构的加速度峰值,将设置障碍物后的加速度峰值下降量与无障碍物时加速度峰值的比值定义为减振率,两种工况减振率分别为12.4%和13.1%.利用傅里叶变换将结构振动响应从时域变换到频域,可以看到结构基频在4.2 Hz 左右,略低于空载时的结构基频4.3 Hz,这是人行桥的柔性特性对行人荷载的敏感所致.
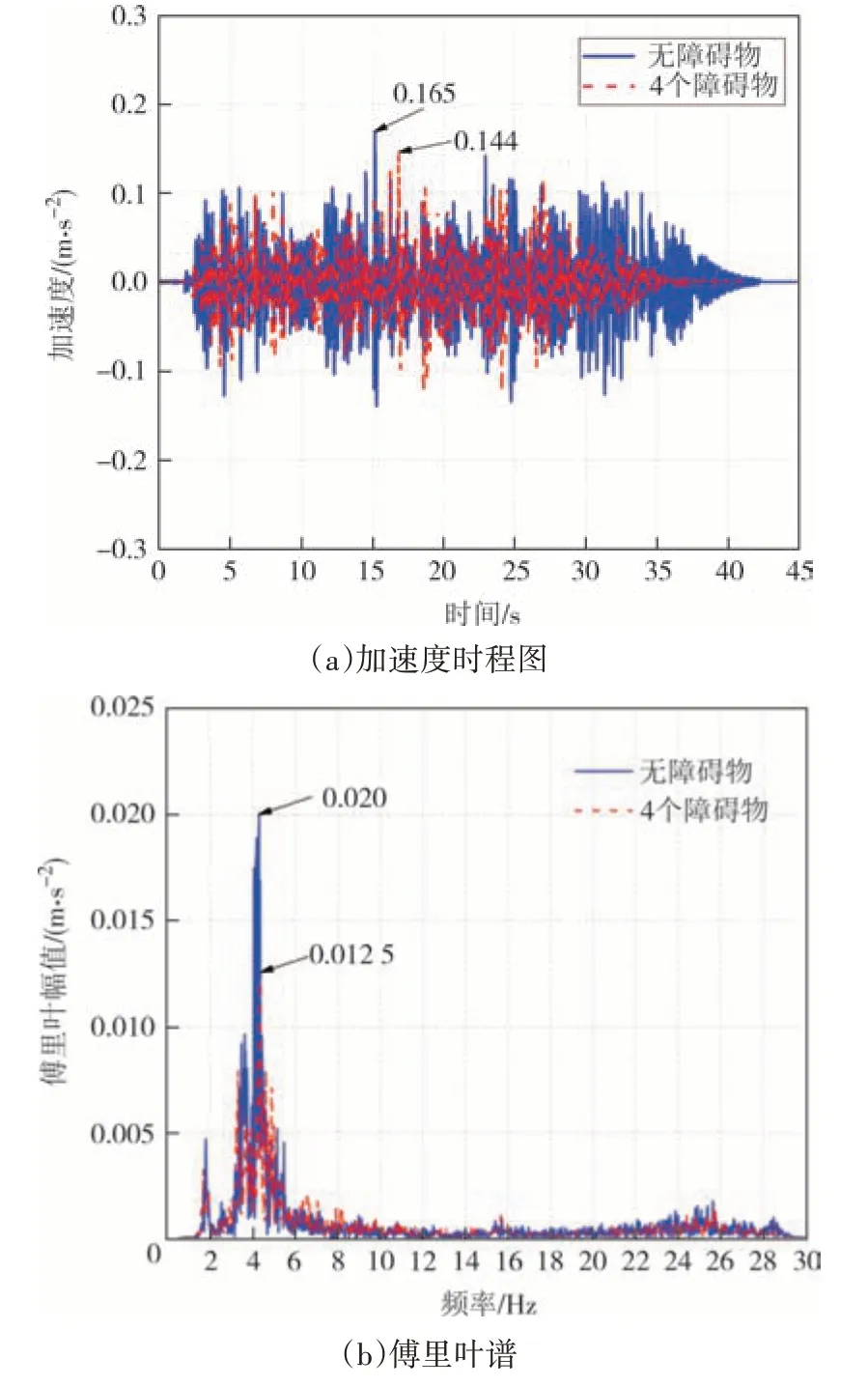
图7 双向各1人实验结果Fig.7 Experimental results of 1 pedestrian each in bi-direction

图8 双向各2人实验结果Fig.8 Experimental results of 2 pedestrians each in bi-direction
3.3 模拟与实验结果对比分析
结合1.2 节中的行人流仿真模拟,在MATLAB平台上建立实验室人行桥并进行以上4 种工况的模拟,为了与实验结果进行对比,设置行人质量均为65 kg,计算结构的加速度响应.图9 呈现了模拟过程当中的行人轨迹图,可以看到,行人在遇到障碍物时可以通过绕行智能地避开,而且行走的轨迹不再单一化,存在一些拐点更能体现真实的行人行走场景.

图9 行人行走瞬态及轨迹线Fig.9 Pedestrian walking transient and pathline
将人行桥视为一维简支梁,结合2.1 节建立人群-结构耦合模型并计算结构加速度响应.图10(a)和图10(b)分别为双向各1 个模拟计算的行人加速度响应时程图和对应的傅里叶谱,设置4 个障碍物后峰值加速度从0.175 m/s2减小到0.166 m/s2,傅里叶幅值从0.027 m/s2减小到0.014 m/s2.同样,对于双向各2 个行人的模拟计算结果如图11 所示,设置障碍物后峰值加速度从0.229 m/s2减小到0.212 m/s2,傅里叶幅值从0.025 m/s2减小到0.017 m/s2.对于双向各1 个行人、2 个行人减振率分别为4.92%和7.6%.详细的模拟数据与实验数据展现在表1 当中,二者结果基本吻合,从表中可以看到每种工况下模拟出来的结构加速度峰值都小于实验采集的结构加速度峰值,这是由于实验室环境复杂,在采集过程当中多多少少会受到外界环境的干扰而影响结果.仿真模拟和现场实验都表明通过合理的布置障碍物可以有效地减少结构的振动.

图10 双向各1人Matlab模拟结果Fig.10 Matlab simulation results of 1 person each in bi-direction
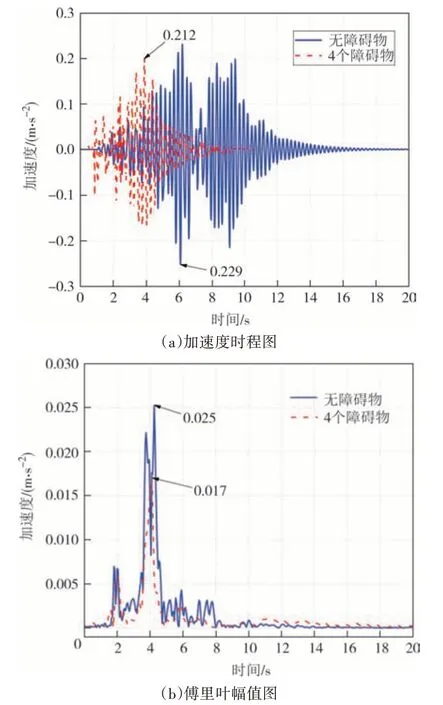
图11 双向各2人Matlab模拟结果Fig.11 Matlab simulation results of 1 person each in bi-direction
4 减振机理
4.1 人群结构能量转化
为了更深入地了解人群流减振的工作原理,Venuti 等[8]开发了一种能量公式应用于动态响应分析当中.从能量的角度看,人群流控制通过修改行人激励的特性以减少传递到人行桥的输入能量,将方程(9)乘以速度,并从动态激励开始的时间0积分到当前时间t,得到:
式中:EKb(t)、EDb(t)、EEb(t)、EIb(t)分别为人行桥的质量动能、粘滞阻尼能、弹性应变能和输入能量.根据式18中的能量转换机制及能量守恒定律说明输入到结构上的能量和输出的能量相等,以实验室人行桥双向各1 人的模拟结果为例,图12 说明了人行桥在无障碍物和布置4 个障碍物时的输入能量和输出能量之间最大误差分别为0.007和0.002,表明两种工况下行人的步行力输入到结构上的能量和结构上产生的三种能量的总和都在误差允许的范围内保持守恒.
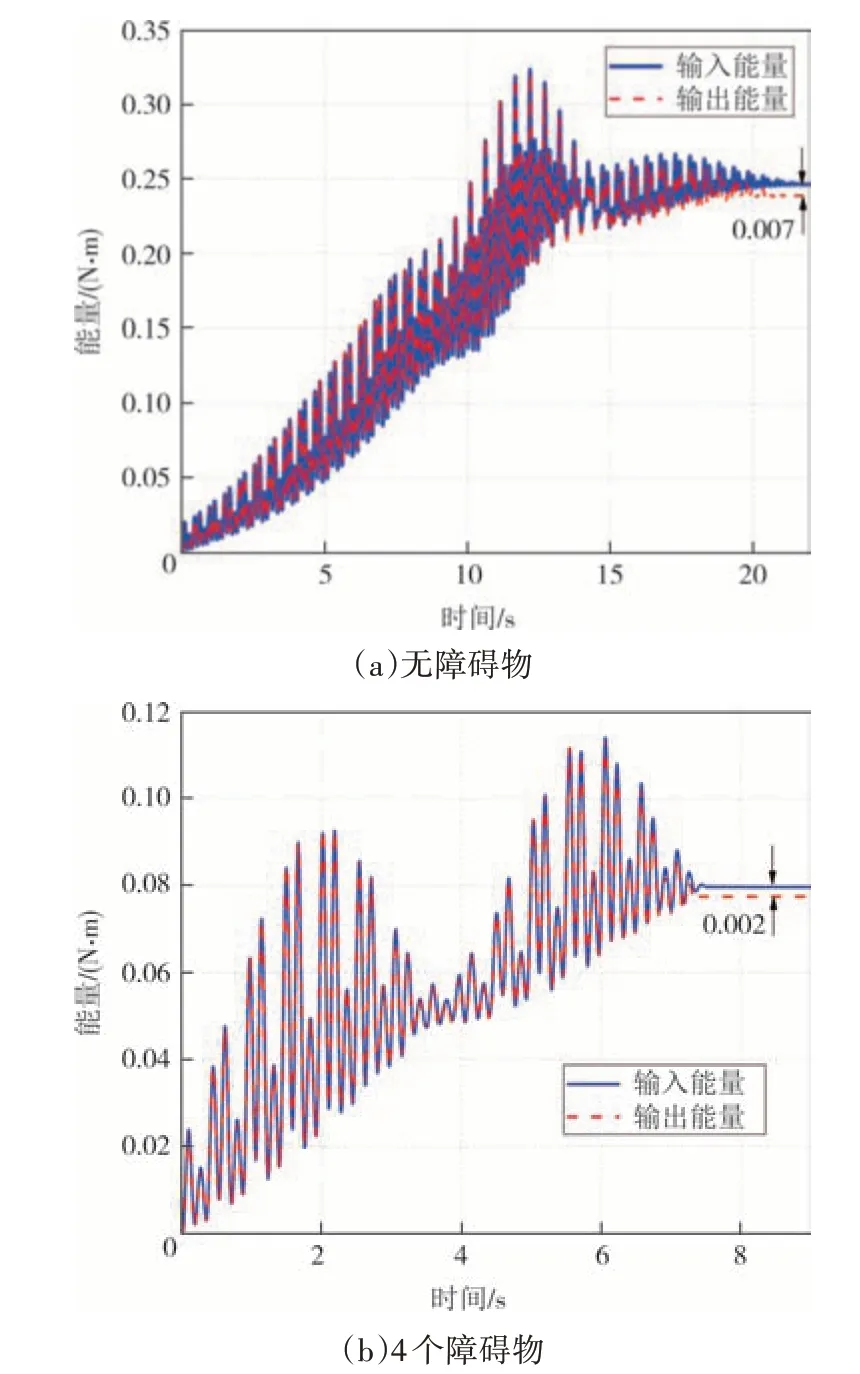
图12 输入、输出能量对比Fig.12 Comparison of input and output energy
4.2 减振机理分析
为了从能量的角度探索设置障碍物可以有效地减小结构振动问题,以实验室人行桥双向各1 人的模拟结果为例,图13 说明了人行桥在无障碍物和设置4个障碍物时结构的EKb、EDb和EEb的时程曲线.通过图13(a)~(c)可以发现,EKb和EEb是随着时间波动的函数,从零开始增加结束时又逐渐减小到零,这是因为随着行人走入结构引起结构振动响应,质量动能和弹性应变能逐渐增加,待行人走出结构且结构响应消失时,这两种能量逐渐减小直至消失.而EDb则从零开始增加并最终收敛于某个数值,该数值就表示输入到结构上的能量.从图13(d)可以看到,在人行桥上设置障碍物控制人群流可以使输入到结构上的能量明显降低,使结构输出的质量动能、粘滞阻尼能和弹性应变能同样都大幅降低,降低率分别达到38.46%、67.48%和50.68%.
5 结论
1)验证了双向人群流的减振策略.在实验室人行桥上进行了双向行人不同人数有无障碍4 种工况下的试验,采集结构的加速度,同时利用MATLAB 进行仿真模拟计算,试验与仿真模拟结果都表明,合理地设置障碍物能够有效地减少结构的振动,算例中的减振率在4%~13%之间.
2)从能量的角度解释了结构的减振机理.设置障碍物使行人步行力输入到结构上的输入能大幅减少,使结构输出的质量动能、粘滞阻尼能和弹性应变能同样都降低.

