玄武岩纤维织物高延性混凝土拉伸性能

邓明科 ，韦鼎 ，张伟 †，董志芳 ，杨铄 ，范洪侃

（1.西安建筑科技大学 土木工程学院，陕西 西安 710055；2.商丘师范学院 建筑工程学院，河南 商丘 476000；3.上海市建筑科学研究院有限公司 上海市工程结构安全重点实验室，上海 200032；4.西安五和土木工程新材料有限公司，陕西 西安 710055）

纤维织物增强砂浆（Textile Renforced Mortar，TRM）是由碳纤维［1］、玻璃纤维［2］或玄武岩纤维［3］等织成的纤维编织网与无机基体结合而成的.纤维材料较强的耐腐蚀性使其保护层厚度仅需满足锚固厚度即可，因此TRM 层可以做得较薄，适用于制作薄壁结构且可广泛应用于加固工程［4-7］.然而TRM 具有以下缺点：基体开裂后不再传递荷载，仅由纤维织物承担荷载；正常使用阶段的拉应力远低于其极限强度；织物与基体的黏结较差，织物在基体中容易滑移，其强度利用率偏低；正常使用极限状态下，裂缝宽度较大等［8］.因此，探究有效的方法以克服TRM 的缺点，改善此类材料的力学性能，对其在实际工程中的推广应用具有重要意义.

Li等［9］指出，将TRM中的砂浆替换为短纤维增强水泥基复合材料，可改进TRM在使用过程中的不足，并且新组成的材料具有更好的裂缝控制能力和拉伸力学性能.高延性混凝土（Highly Ductile Concrete，HDC）是一种聚乙烯醇（Professional Vodeo Assistant PVA）短纤维增强的水泥基复合材料［10-14］，在轴心拉力作用下极限延伸率不低于0.5%且平均裂缝宽度不大于200 μm，具有多裂缝开展和应变硬化特性.董志芳等［15］进行了碳纤维织物以及玻璃纤维织物增强HDC 的单轴拉伸试验，试验结果表明：PVA 短纤维的掺入可有效改善织物与基体的界面特性，使TR-HDC 试件表现出较好的拉伸力学性能.Jiang等［16］通过拉伸试验研究了玄武岩纤维织物与超高延性水泥基复合材料的黏结性能，发现网格间距、纤维嵌入长度均对黏结性能有影响.

玄武岩纤维［17-18］（Basalt Fiber）是以玄武岩为原材料，经1 500 ℃高温熔融制得的.由于具有较大的断裂伸长率、较好的耐热性和化学稳定性，以及较低的价格（仅为碳纤维的1/9），因此玄武岩纤维的应用较为广泛.由文献［15］可知，织物种类的改变导致织物与基体的界面黏结性能有所差异，因此，研究玄武岩纤维织物增强HDC 的拉伸力学性能，并建立理论计算模型具有深远意义.

本文将玄武岩纤维织物与HDC 相结合，通过单轴拉伸试验，研究基体类型、PVA 短纤维掺量、网格间距、织物配网率对玄武岩纤维织物增强HDC 拉伸力学性能的影响.通过理论分析，考虑纤维织物与PVA 短纤维间的耦合作用，建立了玄武岩纤维织物增强HDC 的简化单轴抗拉强度计算模型，为此类材料在工程中的应用提供理论依据.

1 试验概况

1.1 试验设计

试验共设计和制作了36 组纤维织物增强HDC单轴拉伸试件，其中包括9 组对比试件，27 组玄武岩纤维织物增强HDC 试件，每组包含3 个相同的狗骨形拉伸试件.试验变量为：PVA 短纤维掺量、网格间距、织物的配网率、基体类型.PVA 短纤维的体积掺量有5 种：0%、0.5%、1.0%、1.5%和2.0%.网格间距有两种：5 mm、10 mm.织物配网率（ρ）为受力方向上织物的截面面积与拉伸试件截面面积的比值，配网率可通过改变网格间距和织物层数实现［19］，其值见表1.根据前期的工作［20］，本试验选取了表2 所示两种基体配合比，基体中掺入PVA短纤维，其力学性能指标见表3.

试件设计方案如表4 所示.试件编号包括4 部分：玄武岩纤维织物层数、基体类型、PVA 短纤维掺量以及网格间距.例如，“B3M1-1.5-5”表示网格间距为5 mm的3层玄武岩纤维织物增强M1基体试件，且基体中PVA短纤维掺量为1.5%.

1.2 试件设计

由文献［4］可知，TRM 拉伸试件的厚度一般为10～20 mm，宽度为40～80 mm.AC434［21］建议试件标距段的长度不小于50 mm.如图1 所示，本次试验采用的试件总长为350 mm，标距段长150 mm，宽50 mm.加载前，分别在试件两端的正反面黏贴尺寸为100 mm×50 mm和80 mm×45 mm的横、纵向碳纤维布，以防止试件变截面处因应力集中而发生标距段外的过早失效.

图1 狗骨形试件详细尺寸（单位：mm）Fig.1 Dimension of dog-bone specimens（unit：mm）

1.3 材料参数

1.3.1 纤维织物

玄武岩纤维织物是以玄武岩纤维丝为原材料编织成的网格，其表面涂覆环氧树脂胶；网格表面容易湿润，并表现出较高的耐碱性，适用于水泥基复合材料的应用.图2（a）（b）分别展示了网格间距为5 mm、10 mm 的双向均质玄武岩纤维织物，其拉伸性能按照《结构工程用纤维增强复合材料网格》（GB/T 36262―2018）［22］测试，测试过程见图3.纤维束两端采用环氧树脂AB 胶粘贴铝片进行固定，通过夹具将其夹持在试验机上.测试标距段为200 mm，加载速率为1 mm/min，测试结果见表5.

图2 5 mm、10 mm玄武岩纤维织物Fig.2 5 mm，10 mm basalt textile

图3 玄武岩纤维束拉伸测试Fig.3 Tensile test of basalt fiber bundle

1.3.2 基体

HDC 的抗压强度通过100 mm×100 mm×100 mm的立方体试块测得，HDC 的抗拉强度和峰值应变通过图1所示狗骨形试件测得，以上试验结果见表6.

1.4 加载装置

本试验采用电子万能试验机加载，如图4 所示.加载装置包括加载单元和刚性底座两部分，竖向加载单元可提供最大100 kN 的拉力.试件中部装有量程为25 mm 的引伸计，以测量试件标距段内的变形.试验装置的两个端头均采用铰接，其能自由转动，可保证试件在加载过程中始终保持轴心受力.试件的加载程序采用位移控制，加载速率为0.2 mm/min.

图4 加载装置Fig.4 Test set-up

1.5 施工细节

试件制作可分为以下3步：

1）模具中铺设底层基体；

2）放置纤维织物，并轻轻按入底层基体中；

3）铺设顶层基体，抹平表面.

当试件采用多层纤维织物时，只需重复步骤1）和步骤2）至目标层数，然后进行步骤3）.

试件制作时，在钢模具中每铺设一层基体，需振捣密实后再铺设另一层织物，重复此工序，最后浇筑基体并振捣密实，以此保证施工质量，避免纤维织物与纤维织物或纤维织物与基体之间产生孔洞，具体施工步骤如图5 所示.纤维织物之间的基体厚度应不小于2 mm.为保护内部的纤维织物，上下最外层基体厚度应不小于4 mm.试件在浇筑24 h后拆模，标准养护28 d.

图5 施工步骤Fig.5 Construction steps

2 试验结果及分析

2.1 裂缝分布

由表7 可知，当试件中无织物时，如B0M1-0-5、B0M1-0.5-5、B0M1-1.0-5、B0M1-1.5-5 和B0M1-2.0-5，试件的失效模式均呈现单一裂缝开裂.随着织物配网率的增加，试件逐渐表现出明显的多裂缝开裂失效模式，裂缝数量逐渐增多，裂缝间距和宽度逐渐减小.PVA短纤维的掺入，可减缓试件表面的破损现象，改善试件的破坏形态.试件开裂后，由于裂缝处PVA 短纤维的桥联作用，拉伸应力可继续在裂缝周围的基体间传递，使得裂缝间距进一步减小.试件的平均裂缝间距约为网格间距的倍数，这是由于横向纤维束在整个编织网中不承担荷载，仅起到对纵向纤维束的连接捆绑作用；横向纤维束削弱了试件的横截面面积，因此其所在截面处更易出现裂缝［23］.

由表7 和表8 可知，随着织物配网率的增加，M1基体试件的多裂缝开展现象比M2基体更加明显，裂缝间距更小；这主要是由于M1基体中更多未水化的粉煤灰微粒会填实在短纤维与基体界面过渡区，增加界面过渡区的密实性，提高了短纤维与基体的摩擦力，导致最大纤维桥接应力提高，纤维的滑移得到抑制；因此，M1 基体试件裂缝分布更加均匀，裂缝宽度较小［24-25］.网格层数相同时，与网格间距为10 mm 的TR-HDC 试件相比，网格间距为5 mm 的TR-HDC 试件的横向纤维束更多，对试件横截面面积削弱作用更明显，因此其表现出更明显的多裂缝开裂失效模式.

2.2 失效模式

如图6 所示，织物增强试件常见的失效模式有3种［1-2］：（a）试件在标距段端部的破坏；（b）试件内部的织物发生滑移；（c）试件内部的织物发生断裂.试件的失效模式详见表9.

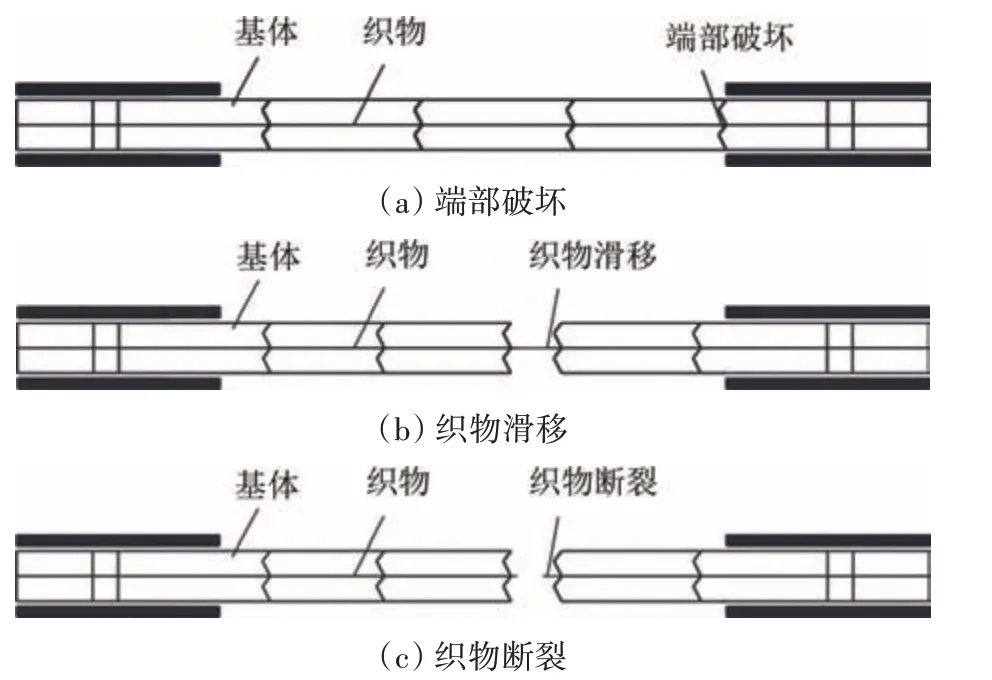
图6 拉伸试件失效模式Fig.6 Failure patterns of tensile specimens

网格间距为5 mm 的织物增强M1 基体试件，在拉伸荷载作用下，PVA 短纤维掺量为1%及以下时，试件的失效模式为织物的断裂和织物的滑移；PVA短纤维掺量为1.5%和2%时，试件的失效模式均为织物的断裂.因此，随着PVA 短纤维掺量的增加，织物与基体的界面特性得到改善，抑制了织物的滑移，改变了试件的失效模式.

PVA 短纤维掺量为1%及以下时，随着织物层数的增加，试件的失效模式更倾向于织物的滑移；PVA短纤维掺量为1.5%和2%时，织物层数的增加未改变试件的失效模式，失效模式均为织物的断裂.

2.3 应力-应变曲线

图7 给出了所有试件在拉伸荷载作用下的应力-应变曲线，表9 给出了各试件特征点的平均值以及织物强度利用率K.K为试件的极限承载力与多根单束纤维承载力之和的比值.

图7 拉伸应力-应变曲线Fig.7 Tensile stress-strain curve

加载初期，试件处于弹性阶段，内部微裂缝缓慢发展，表面没有宏观裂缝，变形较小，荷载主要由基体承担.随后试件进入裂缝开展阶段，由于PVA 短纤维和受力方向纤维织物的桥联作用，拉伸应力仍然能在裂缝处传递，因此既有裂缝附近不断产生新的裂缝，多裂缝开展现象较明显.随着荷载进一步增大，已有裂缝逐渐变宽，并伴随有少量新裂缝的出现.当荷载达到试件的极限承载力时，主裂缝处织物被拉断或产生滑移，导致试件承载力下降，最终发生破坏.

与TRC 试件相比，掺入短纤维的玄武岩纤维织物增强HDC 试件呈现出不同的应力-应变曲线.所有试件在第一阶段均为线弹性，其应力-应变曲线可认为是一条直线.多裂缝开展阶段随着PVA 短纤维掺量和织物配网率的提高而延长.对于TRC试件，织物与基体的黏结强度较弱，试件开裂后，裂缝处织物会产生滑移，如图7（a）、（f）中应力-应变曲线都呈现出不同程度的水平段；PVA 短纤维掺量为1%及以下的TR-HDC 试件，织物与基体的黏结强度虽得到改善，但织物仍有一定的滑移，其应力-应变曲线与TRC 试件相似，可简化为三折线：弹性阶段、多裂缝开展阶段、应变强化阶段.

PVA 短纤维掺量为1.5%和2%的TR-HDC 试件，由于PVA短纤维的桥联作用，织物与基体的界面特性显著改善，拉伸试件呈现出与极限应力相适应的极限应变；此时，TR-HDC 试件的应力-应变曲线与TRC 试件相比波动较小，多裂缝开展阶段从第一条裂缝产生一直持续到试验结束，其应力-应变曲线可简化为二折线：弹性阶段、应变强化阶段.

2.4 因素分析

2.4.1 配网率的影响

如图8 所示，当PVA 掺量相同时，随着织物层数的增加，试件的极限强度和峰值应变大幅提高；TRHDC试件的拉伸强度不是多根单束纤维强度的简单叠加，织物层数的增加会降低纤维织物的强度利用率.

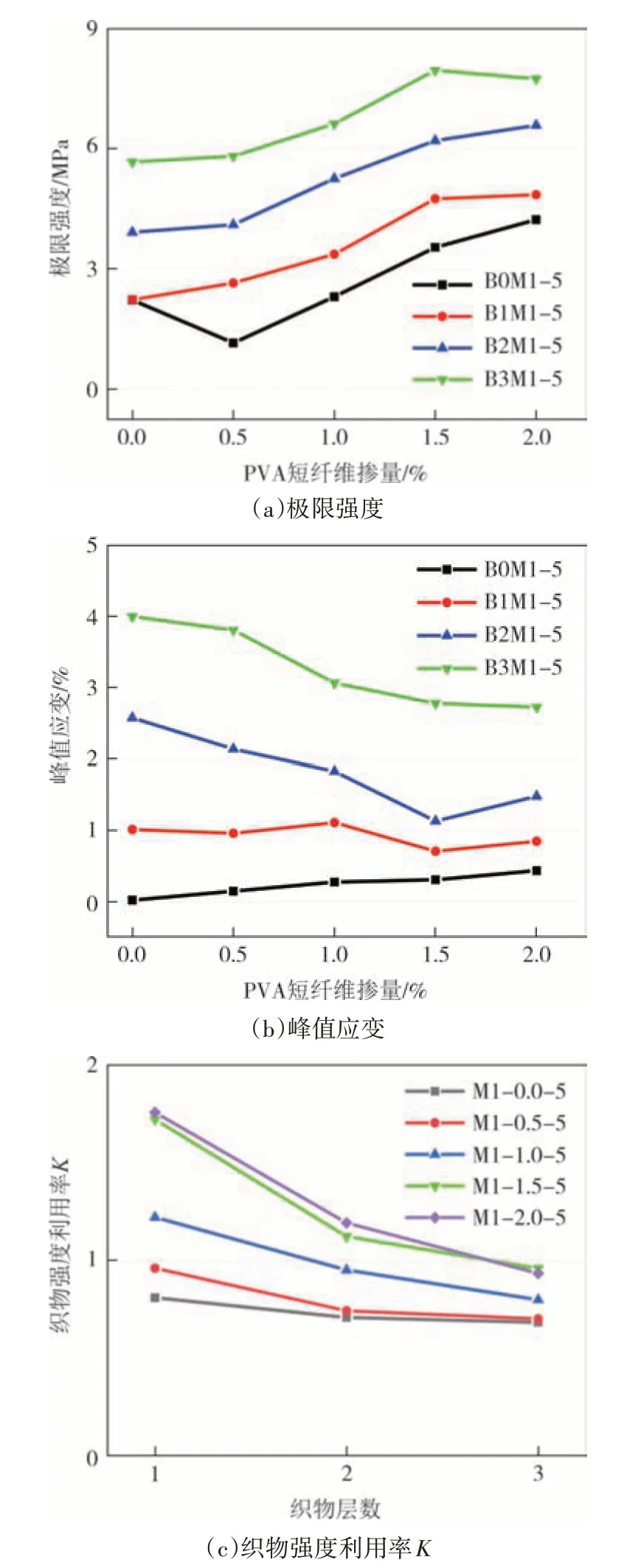
图8 配网率和PVA短纤维掺量对极限强度、峰值应变和织物强度利用率的影响Fig.8 Effect of reinforcing ratio and short PVA contents on tensile strength，peak strain and textile strength utilization

织物与基体的黏结性能对复合材料的力学性能影响较大.文献［19］指出，TRC 中，织物层数的增加降低了纤维束与基体界面的黏结强度，导致织物在达到其抗拉强度之前产生滑移；因此，本试验中，三层织物网格的TRC 试件以及短纤维掺量较少的TRHDC试件，容易发生织物的拔出破坏；当短纤维掺量为1.5%时，所有TR-HDC 试件均发生织物的拉断破坏.

2.4.2 PVA纤维掺量的影响

PVA 短纤维在基体中乱向随机分布，可以桥联裂缝，在裂缝处传递应力，有助于延缓微裂缝的产生；PVA 短纤维的掺入可以提高TR-HDC 试件的抗裂能力，改善织物与基体的界面特性，减少裂纹的发展和织物的滑移.

TRC 试件中，由于织物与基体的黏结性较差，裂缝处织物表现出明显的拔出行为.对于TR-HDC 试件，由“cross-link”模型［26］可知，基体中乱向分布的短纤维附着在织物表面，使织物与基体的界面性能得到改善；因此，在拉伸荷载作用下，织物与基体之间的滑移较少，TR-HDC 试件的失效模式以织物拉断为主.

由图8（b）可知，PVA 短纤维掺量从0.5%增加到1.5%时，TR-HDC 试件的峰值应变呈下降趋势；PVA短纤维掺量从1.5%增加到2%，织物层数为1、2层的TR-HDC试件峰值应变略有增加，织物层数为3层的TR-HDC 试件峰值应变趋于平缓.这是由于PVA 短纤维掺量达到或超过1.5%时，PVA 短纤维为织物与基体之间提供了足够的交联键，阻止了织物的滑移，使织物在裂缝处均表现为拉断，此时TR-HDC 试件的峰值应变由纤维网格和PVA短纤维的拉伸变形共同决定［27］，且PVA 短纤维掺量较高的试件，其应变较高.

2.4.3 基体类型的影响

由表6 可知，PVA 短纤维掺量对HDC 立方体抗压强度影响较小.相比M2 基体的HDC，M1 基体的HDC 由于水泥含量较低而粉煤灰掺量较高，导致其抗压强度较小，拉伸应变较大；其原因是粉煤灰中大部分Ca2+是非游离的，粉煤灰的掺入会稀释基体中Ca2+的浓度，使短纤维与基体的水化程度降低，界面处很难形成强的化学黏结力，导致裂缝处的短纤维更容易脱黏；而未水化的粉煤灰微粒则会附着于纤维与织物表面，增加了界面的摩擦力，使最大纤维桥接应力提高并抑制了短纤维的滑移，导致多裂缝开展现象更加明显，裂缝宽度减小且裂缝分布均匀［24-25，28-29］；因此高粉煤灰掺量的试件会获得更好的拉伸应变能力；同理可知，高粉煤灰掺量的基体中，纤维网格容易获得良好的拉伸应变能力.

如图9 所示，对于PVA 短纤维掺量为1.5%的TR-HDC 试件，当织物配网率相同时，所有试件的拉伸强度差异较小；由此可得，PVA 短纤维掺量为1.5%时，粉煤灰掺量对玄武岩纤维织物增强HDC 的拉伸强度影响较小.

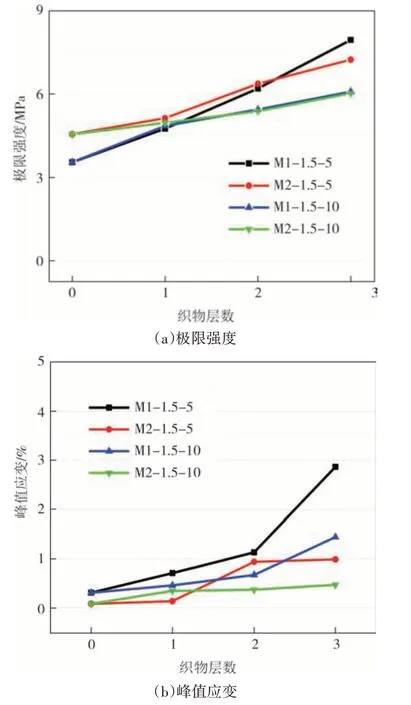
图9 基体类型对极限强度和峰值应变的影响Fig.9 Effect of matrix type on tensile strength and peak strain

2.4.4 网格间距的影响

对于TR-HDC 试件，当织物网格中纤维束的周长相同时，网格间距的变化对纤维织物的黏结强度影响较小；当短纤维较长而网格间距较小时，短纤维不易穿透纤维网格，此时，多数短纤维仅附着于纤维束的单侧表面［16］.

如图10 所示，当PVA 短纤维掺量为1.5%时，与网格间距为5 mm 的TR-HDC 试件相比，网格间距为10 mm 的TR-HDC 试件的织物强度利用率更高；其原因是，网格间距的增加，长度为12 mm 的PVA 短纤维更易穿过纤维网格，此时，短纤维与纤维束的接触面积更大，并且形成类似于钢筋的“销栓作用”，致使其界面性能得到很大的改善；因此，网格间距为10 mm的TR-HDC试件的织物强度利用率更高.

图10 网格间距对织物强度利用率的影响Fig.10 Effect of mesh spacing on textile strength

3 抗拉承载力

抗拉承载力是复合材料力学性能的关键参数，国内外许多学者对于未掺加短纤维的TRC薄板提出了其抗拉承载力的计算方法.由于复合材料内部应力传递的复杂性和观测手段的局限性，目前还不能正确、完整地从微观角度评估.徐世烺等［30-31］依据试验结果从宏观上得出仅考虑纤维利用率的TRC薄板在单轴拉伸时的极限承载力计算公式为：

式中：At为试件截面上沿受力方向纤维织物的面积；ft为纤维织物的抗拉强度；K′为纤维织物的利用率.

式（1）仅考虑了织物配网率的影响，并不能计算掺入短纤维的TRC 试件承载力.董志芳等［15］提出通过与短纤维掺量直接相关的短纤维指数来考虑PVA短纤维对织物增强试件的抗拉承载力的贡献，计算公式为：

式中：kα′为名义纤维织物的利用率；k为织物的理论承载力与织物增强试件的抗拉承载力的比值；α′ 为短纤维指数.

式（2）虽能用于掺入短纤维的TRC 的抗拉承载力计算，但存在以下缺点：初始k值需通过未掺短纤维的试件得到；采用指数计算，有一定的复杂性.

3.1 承载力计算公式

纤维织物增强HDC 试件由纤维织物和高延性混凝土两部分组成，从宏观上看，试件的承载力由纤维织物、高延性混凝土以及二者之间的相互耦合作用共同组成.文献［9］针对TR-ECC 的试验结果表明，当PVA 短纤维掺量为2.0%时，试件的极限荷载并不等于纤维织物和工程用水泥基增强复合材料（Engineered Cementitious Composite，ECC）受拉承载力的简单叠加.由本文试验结果可知，试件的失效模式直接由纤维织物的拉断或滑移控制，即极限抗拉强度由纤维织物控制.PVA 短纤维的加入改善了织物与基体的界面特性，对承载力的影响通过织物强度利用率的提高来反映.因此，本文仍假定抗拉承载力主要由纤维织物承担，然后提出同时考虑短纤维掺量和织物配网率的承载力计算公式，公式如下：

式中：K为纤维织物强度利用率；α为与短纤维掺量和织物配网率相关的常数；a、b为系数，其值与纤维织物和短纤维类型有关.

对于网格间距为5 mm 的玄武岩纤维织物增强M1基体试件，由图8（c）可知：当织物配网率一定时，短纤维掺量的增加提高了织物强度利用率，并在短纤维掺量达到2%时织物强度利用率达到最大；当短纤维掺量一定时，织物配网率的增加降低了织物强度利用率.

根据短纤维掺量（v）、织物配网率（β）与织物强度利用率的关系，本文将v、β简化为α，关系见式（5）.

由式（5）可知：当v恒定时，α随β的增大而降低；当β恒定时，α随v的增大而增大.这与本试验和文献［15］所反映的结论一致，因此用α来反映短纤维掺量和织物配网率之间的关系是合适的.

忽略基体类型的影响，通过对本试验中27 组玄武岩纤维织物增强HDC 拉伸试件结果的平均值进行拟合分析，可以确定a、b的取值.α与K经拟合分析得到的回归直线如图11 所示，确定的a、b数值及对应的标准误差见表10.度量拟合优度的可决系数R2=0.917，接近于1.0，这说明假定的线性关系完全适用，且可通过进一步增加样本容量来减少a、b的误差.

图11 线性拟合分析Fig.11 Linear fitting analysis

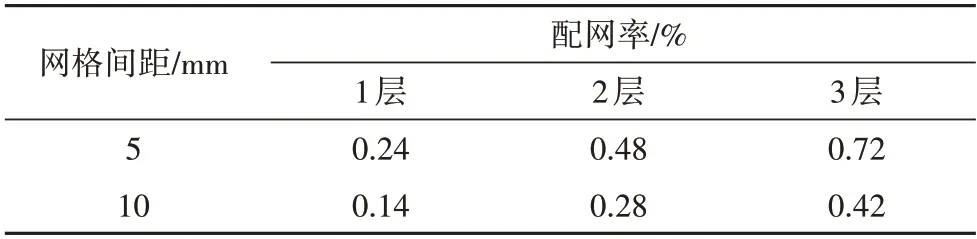
表1 玄武岩纤维织物配网率Tab.1 Ratio of basalt textile grids

表2 基体配合比Tab.2 Mixed proportions of matrices kg·m-3

表3 PVA短纤维力学性能指标Tab.3 Mechanical performance indicators of short PVA fibers

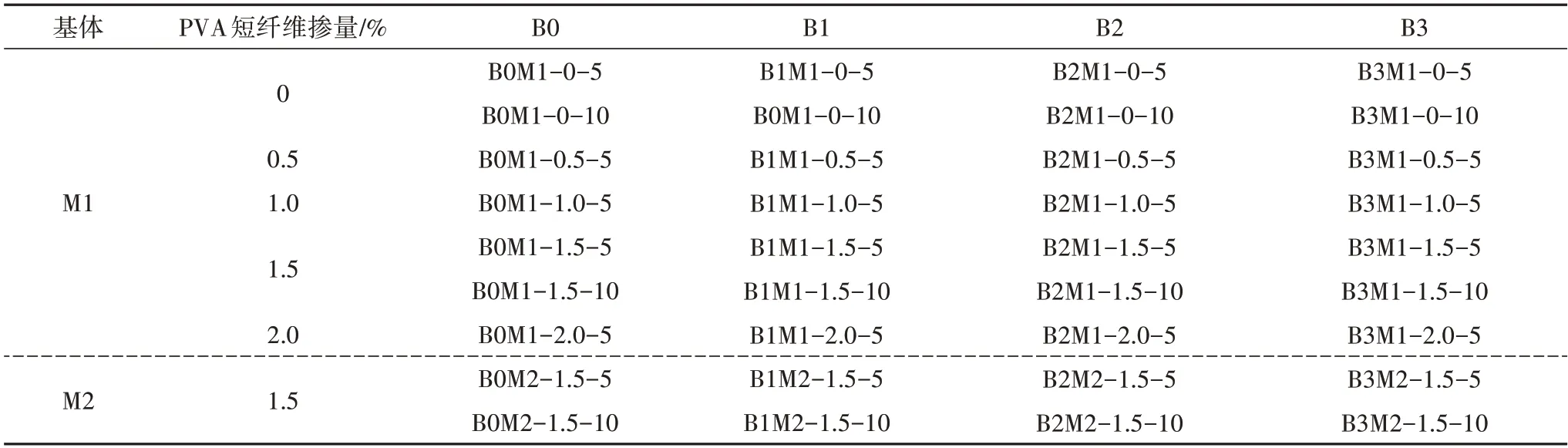
表4 试件设计方案Tab.4 Specimens design plan

表5 玄武岩纤维织物力学性能Tab.5 Mechanical properties of basalt textile

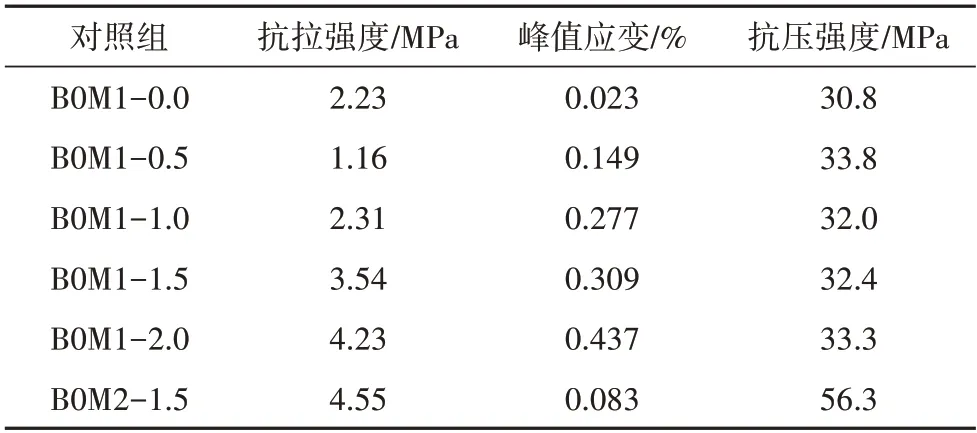
表6 基体力学性能Tab.6 Mechanical properties matrix

表7 网格间距5 mm的试件开裂模式Tab.7 Cracking pattern of specimens with 5 mm mesh spacing

表8 网格间距10 mm的试件开裂模式Tab.8 Cracking pattern of specimens with 10 mm mesh spacing

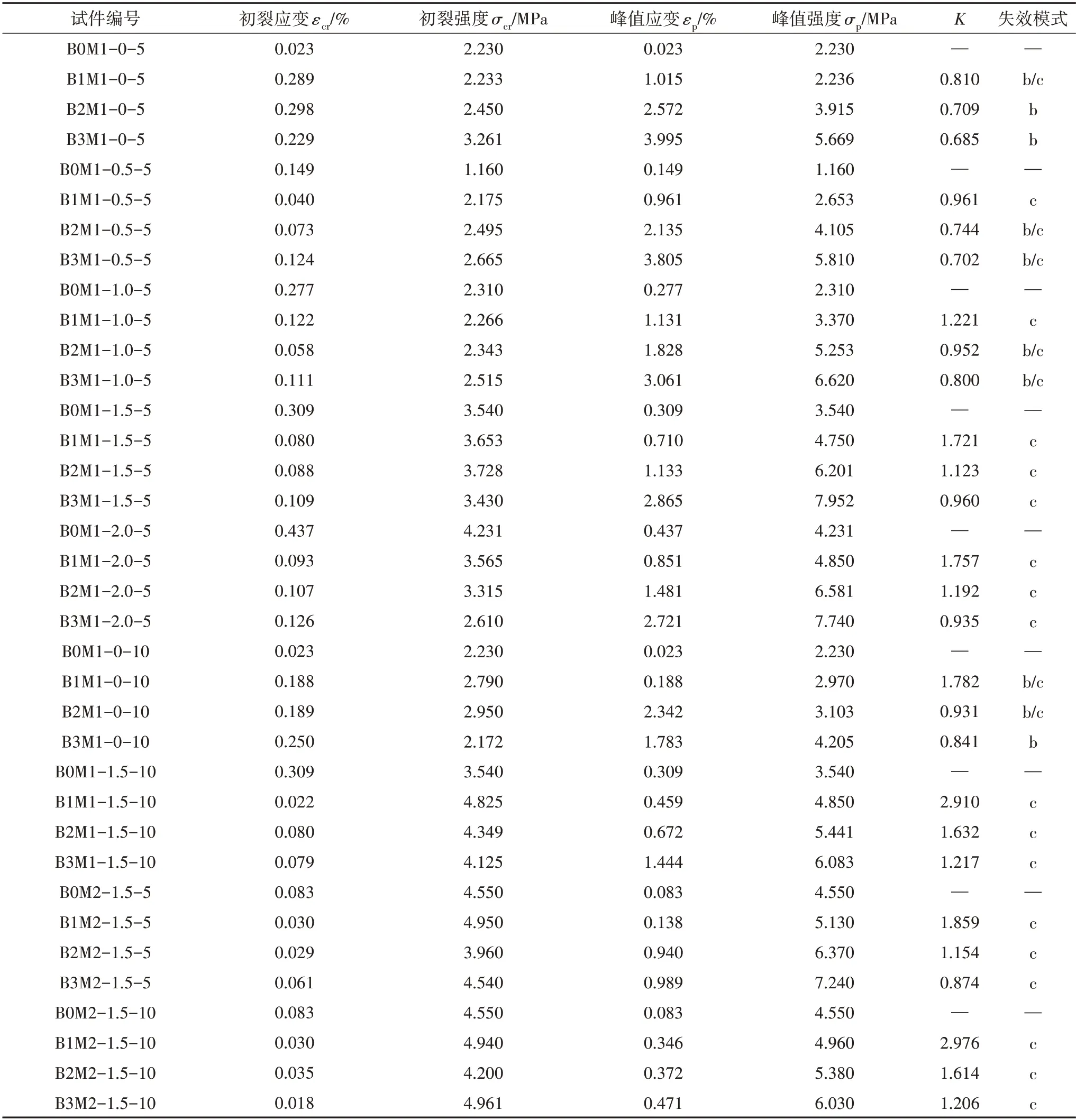
表9 试验结果汇总Tab.9 Summary of test results

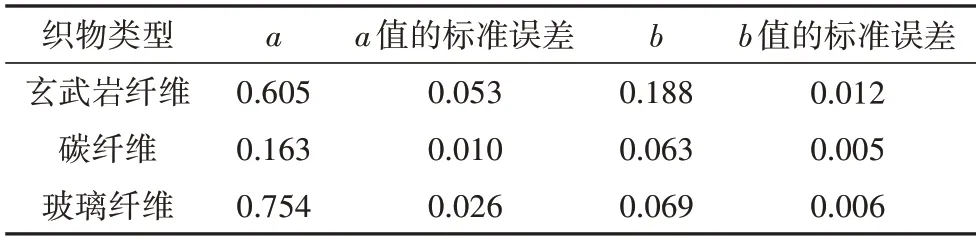
表10 常数a、b取值及标准误差Tab.10 Values of a and b and standard errors

用本文提出的承载力计算公式来计算文献［15］中碳纤维织物增强HDC试件（CTR-HDC）、玻璃纤维织物增强HDC试件（GTR-HDC）的抗拉承载力，回归直线见图11.碳纤维织物、玻璃纤维织物的可决系数分别为0.895和0.888.确定的a、b数值及对应的标准误差见表10.

由图11可知：三种纤维织物增强HDC 试件的织物强度利用率差别较大.这是由于不同纤维织物与基体的界面黏结性能不同，导致纤维织物在复合材料中抗拉强度发挥能力产生差异.

3.2 抗拉强度计算公式

纤维织物增强HDC 的抗拉强度是其力学性能的关键参数，将式（3）除以试件的截面面积A，则可得到不同织物配网率和不同PVA 短纤维掺量下，纤维织物增强HDC的抗拉强度计算公式：

式（6）可用于计算不同织物配网率和PVA 短纤维掺量下，网格间距为5 mm 和10 mm 的玄武岩纤维织物增强HDC 的抗拉强度，为工程实际中的设计、应用提供了理论依据.

4 结论

1）对于玄武岩纤维织物增强HDC 试件，配网率的提高，试件的极限强度和峰值应变随之提高，但织物强度利用率降低；PVA 短纤维掺量的增加，提高了试件的极限强度和织物强度利用率，但峰值应变下降.

2）随着织物配网率的提高，试件呈现出典型的多裂缝开展特征，裂缝间距和宽度逐渐降低.PVA短纤维的掺入可减少织物的滑移，改善试件的破坏形态.

3）基体中粉煤灰掺量的变化对玄武岩纤维织物增强HDC 试件的抗拉强度影响较小，而粉煤灰掺量较高的试件，峰值应变提高.

4）当PVA 短纤维的长度大于网格间距时，随着网格间距的增大，PVA 短纤维更多地附着于纤维束表面，提高了TR-HDC试件的织物强度利用率.

5）根据试验结果提出同时考虑短纤维掺量和织物配网率的耦合作用系数，可用于计算不同PVA 短纤维掺量下，网格间距位5 mm 和10 mm 的玄武岩纤维织物增强HDC的抗拉强度.