考虑黏结滑移与剪切效应的不均匀冻融损伤RC 剪力墙数值模型

荣先亮 ，卢博辽 ，张琦玉 ，黄炜元 ，郑山锁 ，张艺欣

［1.同济大学 土木工程学院，上海 200092；2.先进土木工程材料教育部重点实验室（同济大学），上海 201804；3.西安建筑科技大学 土木工程学院，陕西 西安 710055；4.华侨大学 土木工程学院，福建 厦门 361021］

众所周知，寒冷地区的冻融循环作用是混凝土力学性能下降的主要原因之一［1-5］.近几十年来，在加拿大的育空地区、美国北达科他州，冻融作用导致钢筋混凝土（Reinforced Concrete RC）构件（含梁、柱、剪力墙）的损伤引起了诸多学者广泛的关注，并针对其静力荷载作用下的力学性能（弯曲、剪切）展开了研究［3-4］.与此同时，Yang 等［6］、Rong 等［1，7］的研究指出：位于严寒地区的在役钢筋混凝土（Reinforced Concrete RC）剪力墙亦处在抗震设防区中，面临巨大的地震灾害威胁［8］.因此，对冻融损伤RC 剪力墙展开抗震性能评估具有重要意义.但据作者所知，目前关于RC 剪力墙抗震性能评估的数值模型（纤维模型［9］、多垂直杆模型［10］、分层壳模型［11］、固角桁架杆模型［12］）均是基于完好构件的，鲜有可用于冻融损伤RC 剪力墙抗震性能评估的数值模型.鉴于此，有必要建立可准确评估冻融损伤RC剪力墙的数值模型.

冻融循环作用后混凝土的力学性能及其与纵筋间的黏结性能降低，尤其是在较大冻融循环次数（Number of Freeze-thaw Cycles，NFTCs）下此种降低更加明显［1，3，5，7，13-14］.与此同时，冻融损伤呈较为明显的不均匀分布特征，由混凝土构件表面开始逐渐渗透至构件内部［1，5-7，13］.因此，在建立冻融损伤RC剪力墙数值模型时，首先需要进行的是不均匀冻融损伤的合理考虑，包括混凝土强度的不均匀冻融损伤和黏结滑移的不均匀冻融损伤.此外，Rong等［1，7］、Yang等［6］的研究表明：冻融作用可降低RC 剪力墙的抗剪性能，增加其剪切变形；300次冻融循环后，剪跨比为2.14 的RC 剪力墙其峰值点的剪切占比由23.25%（NFTCs=0）上升至65.61%（NFTCs=300）［1］.因此，在建立冻融损伤RC 剪力墙数值模型时，还需充分考虑剪力墙的剪切效应.

考虑到多垂直杆模型［10］、分层壳模型［11］、固角桁架杆模型［12］均未在剪力墙构件厚度方向进行精细划分，故其无法实现冻融损伤不均匀性的考虑.纤维模型沿构件厚度方向将截面划分为诸多混凝土纤维和钢筋纤维，可依据冻融损伤分布的不均匀特征，建立损伤修正模型对不同截面处的混凝土纤维本构进行不同程度的折减，实现冻融损伤不均匀性的考虑.然而，值得指出的是，传统的纤维模型未考虑黏结滑移和剪切作用［15］.

针对未考虑剪切效应问题，一些学者［16-18］提出在截面层次添加剪切-剪应变（V-γ）恢复力模型形成组合剪切的纤维截面模型，实现了对剪切效应的考虑；进而利用此模型对剪切变形较为显著的完好RC剪力墙展开模拟并取得了较为准确的模拟效果.针对未考虑黏结滑移效应问题，Zhao 等［19］提出采用钢筋黏结滑移模型替换纵筋本构，通过底部串联替换后的零长度纤维截面单元进行构件的模拟，实现了对黏结滑移效应的考虑，并通过完好RC 结构对其准确性进行了有效验证.然而，值得指出的是，Zhao等［19］所提出的方法难以考虑因冻融作用所导致的黏结强度衰减，且关于滑移值的计算公式来源于经验回归，其准确性有待于进一步的验证与提升.

综上，本文结合冻融损伤特征与冻融作用的影响依次建立了不均匀冻融损伤模型［5］、冻融损伤剪切恢复力模型、不均匀冻融损伤黏结强度和滑移模型（理论推导），并对所建各模型的准确性进行了验证.利用不均匀冻融损伤模型对RC 剪力墙纤维截面所划分的混凝土本构进行折减实现了冻融损伤的合理考虑；在此基础上，组合剪切恢复力模型所表征的剪切效应实现了RC 剪力墙的抗剪；同时，在墙底串联包含纵筋黏结滑移模型的零长度截面单元从而建立了可综合考虑弯曲、剪切、黏结滑移效应的冻融损伤RC 剪力墙数值模型.最后，通过8 个既有冻融损伤RC 剪力墙的拟静力试验结果，从滞回曲线和骨架曲线两个方面验证了本文所提数值模型的准确性.研究可为冻融损伤RC 剪力墙的抗震性能评估提供参考.

1 试验简介

为探究冻融循环作用下RC 剪力墙抗震性能的变化，对8 根剪跨比为2.14 的冻融损伤RC 剪力墙进行了拟静力试验.剪力墙的参数设置见表1.试验墙几何尺寸及详细配筋布置见图1（a）.竖向分布筋和箍筋采用HPB235（直径6 mm），其实测屈服强度为270 MPa，极限强度为470 MPa，弹性模量为2.1×105MPa.暗柱纵筋采用HRB335（直径12 mm），其实测屈服强度为409 MPa，极限强度为578 MPa，弹性模量为2.0×105MPa.

图1 几何尺寸与加载方案Fig.1 Geometry and loading scheme

表1 剪力墙试件的关键参数Tab.1 Key parameters of the shear wall specimens

采用人工气候模拟冻融环境对各RC 剪力墙进行冻融循环试验，待达到各设计NFTCs（见表1）时对其进行拟静力加载.拟静力加载方案见图1（b）；屈服前采用荷载控制加载，每级加载循环一次；屈服后采用位移控制加载，每级加载循环三次.详细的位移计布置如图1（b）所示，量测的特征点荷载与变形见表1.更为具体的试验细节参见Rong等［1］的研究.

2 建模思路

Petersen［5］基于相对动弹性模量ERDM实测值验证了冻融损伤在构件截面内的分布具有不均匀性.Yang 等［6］、张德义等［2］和Rong 等［1，7］的试验亦观察到了冻融损伤在试件内部呈不均匀分布的现象.鉴于冻融损伤的分布特征，本文选用纤维模型（见图2 和图3），并通过建立不均匀损伤模型以实现冻融损伤的合理考虑.图3 显示了冻融损伤剪力墙的纤维截面划分，不同的颜色代表不同的冻融损伤程度，且冻融损伤程度由外向内逐渐减小.此外，水平循环荷载作用下的墙顶总变形由三部分组成：弯曲、剪切和黏结滑移.纤维模型只考虑了构件的弯曲性能，而忽略了构件的剪切性能与黏结滑移效应.与此同时，已有研究均表明：冻融损伤削弱了钢筋与混凝土间的黏结强度以及剪力墙的抗剪能力，增大了剪切变形（见表1）与黏结滑移变形［1，6-7，13-15］.为此，本文通过构建考虑冻融损伤的剪切恢复力模型，并在截面层次上将所建立的剪切恢复力模型添加到所建立的考虑不均匀冻融损伤的纤维截面上形成组合剪切效应的纤维截面［16-18］，实现了纤维单元剪切效应的考虑；对应的组合示意图如图2 所示.基于已建立的考虑冻融损伤与剪切的纤维模型，在墙底添加零长度截面单元［19］，实现了黏结滑移效应的考虑.对应的建模示意图如图3 所示.具体的实现是通过建立考虑冻融损伤的钢筋滑移模型，然后将所建立的黏结滑移模型替换掉零长度截面弹簧单元中的普通钢筋本构.整体模型的建立方法列于图3.其中：两端暗柱箍筋约束范围内均为约束混凝土纤维，其余均为无约束混凝土纤维.由此可见，准确建立不均匀冻融损伤模型、冻融损伤剪切恢复力模型以及冻融损伤纵筋滑移模型成为本文数值模型的关键.因此，下文依次对其建立过程展开了详细的描述.

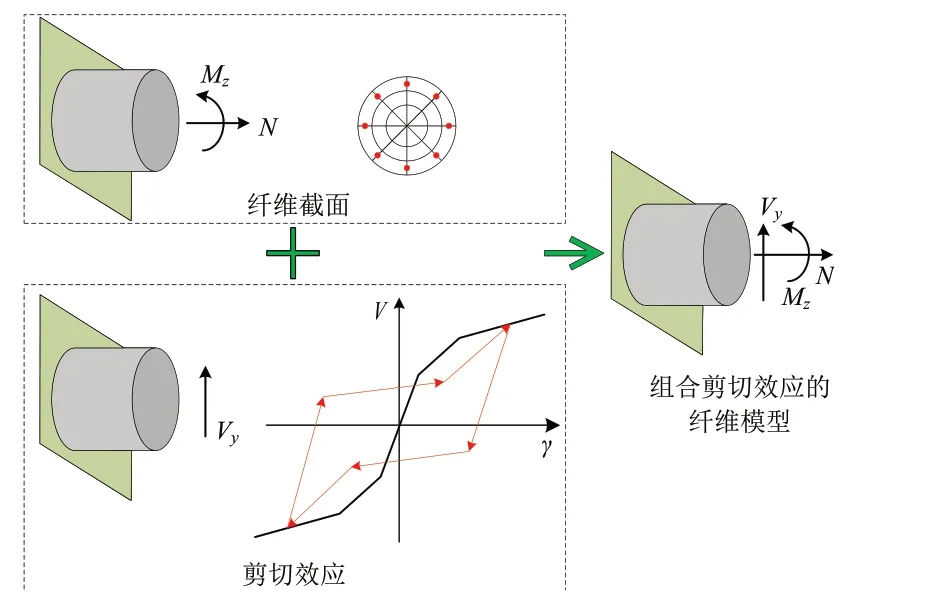
图2 组合剪切的纤维截面Fig.2 Fiber section considering shear effect

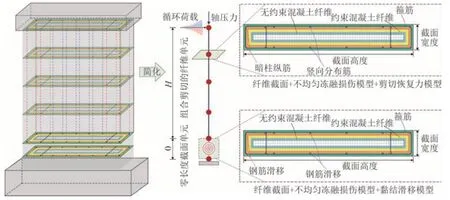
图3 冻融损伤RC剪力墙模型Fig.3 Proposed model of frost-damaged RC shear wall

3 不均匀冻融损伤模型

本章以ERDM为冻融损伤系数并作为联系冻融损伤混凝土强度和动弹性模量的桥梁，通过修正不同位置处完好混凝土本构建立了不均匀冻融损伤混凝土模型.具体的实现是通过OpenSees 中的循环语句.详细流程见图4，其对应的计算步骤如下：

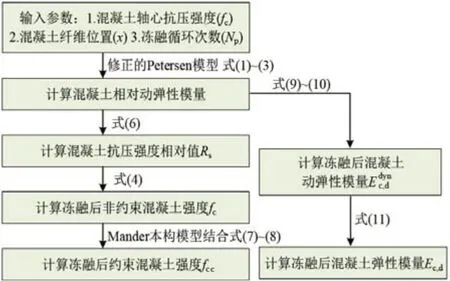
图4 不均匀冻融损伤模型计算流程Fig.4 Calculation flow of non-uniform freeze-thaw damage model

1）确定未冻融混凝土本构参数，包括弹性模量Ec、非约束（约束）混凝土峰值应力fc（fcc）、峰值应变εc（εcc）以及极限应变εcu（εccu）等.

2）基于已建立的修正Petersen 模型（图5），计算给定NFTCs下不同截面位置处混凝土的冻融损伤系数ERDM.ERDM取公式（1）和（2）的较大值，对应如下：

图5 修正的Petersen模型［5］Fig.5 Modified Petersen model［5］

式中：Np为RILEM TC176-IDC［20］冻融制度下的NFTCs；N′p为冻融循环次数临界值，其值由混凝土纤维所在截面的位置确定，具体计算式如式（3）：

式中：d为混凝土纤维位置与截面受冻边缘间的距离，取最小的冻融深度，如图6所示.

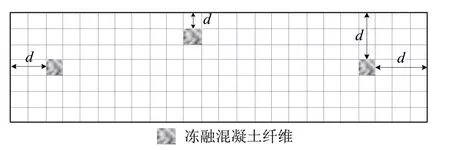
图6 混凝土纤维冻融深度Fig.6 Freeze-thaw depth with concrete fibers

3）通过多参数回归分析构建了冻融损伤后混凝土纤维强度模型.其建立过程如下.

Liu 等［21］的研究表明，提高混凝土初始强度可提高相对抗压强度，且提高的程度呈增加趋势.因此，在建立冻融损伤混凝土强度计算式时将其假定为关于初始强度fc的幂函数形式；同时，结合边界条件，将冻融损伤混凝土强度fc，d、冻融后的相对抗压强度Rs计算式假定为：

式中：a、b是拟合参数，其值通过对收集到的试验数据［21］进行多参数拟合得到，相应的计算式如式（6），对应的计算结果如图7所示.

图7 非约束混凝土冻融后强度计算结果Fig.7 Strength calculation results of unconstrained concrete after freezing and thawing

4）冻融后截面不同位置处的约束混凝土强度fcc，d折减系数β值与相同冻融深度处非约束混凝土强度折减系数相同.鉴于此，得到：

5）依据张艺欣等［13］的研究计算未冻融混凝土的动弹性模量：

7）根据式（1）～（2）即可得到冻融损伤混凝土的弹性模量：

综上，给定Np与xi，根据未冻融混凝土本构参数，结合公式（1）～（11），即可计算出不同位置处的冻融损伤混凝土纤维本构参数，即构建了由表及里的不均匀冻融损伤模型.

4 冻融损伤RC剪力墙剪切恢复力模型

OpenSees 中的Hysteretic 模型能较全面地反映剪力墙的剪切滞回特性.基于此，利用该模型构建剪力墙的剪切滞回模型（见图8），从而实现纤维截面剪切效应的考虑.图8中Vc、Vy、Vm依次为剪力墙剪切骨架曲线的开裂剪力、屈服剪力、峰值剪力；Ka为剪力墙初始抗剪刚度.

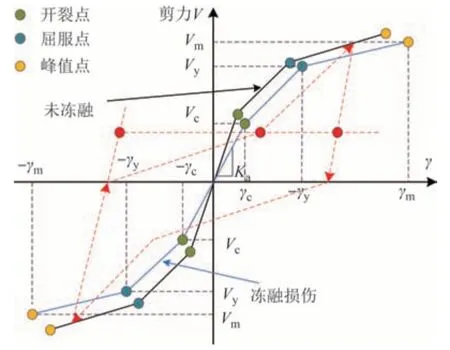
图8 剪切恢复力模型Fig.8 Shear hysteretic model

4.1 完好RC剪力墙剪切恢复力模型

基于前文试验结果得到的剪力与剪应变变化趋势，本文将完好与冻融损伤RC 剪力墙剪切骨架曲线简化为图8 所示的三折线型.其中，完好RC 剪力墙试件各特征点剪力V、剪应变γ采用经准确性验证的公式进行计算［17-18，22］.

1）开裂剪力Pc［23］

式中：fc是轴心抗压强度，psi（原文公式中单位，1 MPa=145 psi）；N是轴压力，Pa；A为试件截面面积，in2（原文公式中单位，1 in2=645.16 mm2）.

式中：λv为配箍特征值；λ为剪跨比；Pm为峰值剪力.

式中：ft是抗拉强度；hw0、bw分别是构件截面有效高度和厚度；fyh、Ash、sh分别是水平分布筋屈服强度、截面面积以及钢筋间距；Aw为剪力墙腹板面积.

式中：Ka为剪力墙初始抗剪刚度；Es是钢筋弹性模量；As是截面钢筋的面积；Ec是混凝土弹性模量；ν为泊松比（取0.2）；χ为形状系数.

式中：αs为开裂后剪力墙刚度与初始剪切刚度Ka的比值；fwh、ρwh分别为水平分布筋强度和配筋率.

6）峰值剪应变γm

式中：Ks是剪力墙塑性铰区抗剪切刚度，计算式见式（19）［22，27］.

式中：hw、tw分别为墙宽和墙厚.

4.2 冻融损伤RC剪力墙剪切恢复力模型

目前，已有诸多学者［1，5，7，13-14］采用ERDM来定量表征混凝土的冻融损伤程度.Rong 等［1］以ERDM为指标建立了可表征冻融损伤程度的冻融损伤参数D：

式中：F为基于人工气候冻融条件下的NFTCs.

由表1的实测值可见：随NFTCs、fc、n的增加，剪力和剪应变均发生不同程度的变化.基于此，综合考虑NFTCs、fc、n的影响，选取n和D为参数，对未冻融墙体的剪力和剪应变进行修正，对应公式如式（21）（22）：

式中：Pi′（Pi）、γi′（γi）分别为冻融损伤（完好）墙体特征点i的剪力与剪应变；fi(D，n)、ri(D，n)分别为特征点i的剪力与剪应变修正函数，由表1 的试验值归一化后的系数经多参数非线性曲面拟合得到，详细的建立过程可参见郑山锁等［28］的研究.

1）开裂剪力和剪应变

2）屈服剪力和剪应变

3）峰值剪力和剪应变

4.3 准确性验证

利用4.1节的公式计算出完好RC 剪力墙特征点的剪力和剪应变，进而利用式（23）～（28）得到冻融损伤剪力墙特征点的剪力和剪应变.依据计算数据绘制了图9 的误差分布.由图9 可见：剪力和剪应变的计算值与试验值吻合良好，计算值的误差不超过20%.其中：计算开裂、屈服、峰值剪力和试验比的均值是1.003、0.978、1.073，相应剪应变之比的均值是0.911、0.981、1.042，表明所提出的剪切骨架曲线特征点计算模型能较好地反映冻融损伤RC 剪力墙在低周往复下的剪切性能.

图9 误差分布Fig.9 Error distribution

5 不均匀冻融损伤黏结滑移模型

图10 显示了纵筋滑移转角.本节首先结合既有材性实测数据与前文所建立的冻融损伤模型建立了不均匀冻融损伤黏结强度模型；依据已有未考虑冻融的纵筋滑移模型对锚固区不同深度处黏结应力进行冻融损伤修正，进而采用理论方法建立了考虑不均匀黏结应力分布的冻融损伤纵筋滑移模型，并对其进行了验证.

图10 端部纵筋滑移变形Fig.10 Slip of end longitudinal reinforcement

5.1 不均匀冻融损伤黏结强度模型

通过收集已有拉拔试验的黏结强度数据［14-15］（图11），对其进行回归分析并建立了相对黏结强度τd/τ0与ERDM间的计算式，见式（29）.结合冻融损伤程度随NFTCs和纤维位置的关系，见式（1）～（3）.构建了黏结强度τd/τ0随NFTCs 和纤维位置的计算关系，即不均匀冻融损伤黏结强度模型，见式（30）.

图11 τd/τ0和ERDM的计算关系［14］Fig.11 Calculation relationship between τd/τ0 and ERDM［14］

式中：τ0为未冻融钢筋屈服前的平均黏结应力；τd为冻融损伤后的黏结应力.

5.2 未冻融纵筋滑移模型

目前，宏观模型与微观模型均认为锚固区滑移是由端部纵筋受拉应力渗透至锚固区产生的，即应力渗透长度ld内钢筋应变ε(x)的累积，相应计算式为：

同时，该范围内的钢筋应力fs与混凝土提供的黏结应力相等，即：

式中：db、As分别为纵筋直径和截面面积.

宏观模型通过将式（31）中的核函数转变成近似的常数，显著简化了计算.鉴于此，本文沿用Sezen等［29］的宏观模型建立了完好纵筋滑移模型，见图12（a）.结合式（31）（32）解出纵筋屈服前、屈服后的滑移量s：

图12 纵筋滑移模型Fig.12 Longitudinal bar slip model

其中：ld分别为钢筋屈服前、后的应力渗透长度，计算公式如式（34）（35）.

式中：εs为钢筋应变；εy为钢筋屈服应变；为钢筋屈服后的平均黏结应力.

5.3 不均匀冻融损伤纵筋滑移模型

依据前述构建的不均匀冻融损伤τd/τ0模型［见式（30）］，在一定锚固高度，冻融损伤黏结强度τd和位置变量d成线性变化.为便于后文推导，依据锚固端边界条件，即应变和应力等于零（fs=0，εs=0，x=0）建立坐标系，则d在此坐标系下为：

式中：ld，d是冻融损伤后的应力渗透高度.基于此，黏结强度模型可表示为：

式中：a、b是模型系数；d0是与NFTCs 对应的冻融损伤深度，表征黏结强度仅在d0内衰减.依据式（3）解得：d0=0.943N+0.226.同时结合前文所建的冻融损伤τd/τ0衰减模型解出：a=-0.010 9τ0，b=(0.010 9ld，d-0.010 3N+1.018 7)τ0.

钢筋进入塑性后，τ′0替代τ0.同时，假定钢筋本构为双线型，其弹性模量为Es，应变硬化率为Esh/Es；对应的滑移模型见图12（b）.下文介绍钢筋屈服前、后s的推导.

1）屈服前

由于在x范围内黏结应力呈梯形分布，故前述力的平衡方程（32）可转变成：

式中：τ0，d是弹性段冻融损伤端部截面钢筋黏结强度，依据式（37）计算.可以看出，给定应力fs下，式（38）是关于x的一元二次方程.对其进行求解，并舍去负解，即得出关于x的唯一正解.同时，在应力渗透高度内取长度dx的微段，见图12（b）.该脱离体两端应力增量dfs(x)与周围黏结应力保持相等：

结合式（38）与边界条件（fs=0，x=0），对式（39）进行求解，得：

依据式（33）计算s：

上述理论推导均是基于应力渗透高度小于冻融损伤深度d0的条件.当应力渗透长度进入未冻融范围内时，转变成5.2 节Sezen 模型［29］进行求解.至此，屈服前钢筋s归结为：

2）屈服后

屈服后钢筋sd的推导和屈服前相似.首先基于力的平衡方程求解屈服后关于x′的一元二次方程：

式中：fs为钢筋强度；fy为钢筋屈服强度；τ′0，d是塑性阶段冻融损伤后端部界面的黏结强度，可依据式（38）求解.基于此，并舍去关于x′的负根，得x′的唯一正根.总的s是屈服后sy与塑性段后的滑移量之和：

式中：Esh为钢筋进入塑性阶段后的弹性模量；钢筋应力fs(x′)采用和式（40）相同的方法对微段平衡方程两端积分，结合边界关系（fs=fs，x′=0）得：

结合式（43）～（45）得s为：

5.4 试验验证

选取文献［30］的黏结应力分布实测值，即在分级加载拉拔试验中量测了冻融损伤钢筋应变沿锚固长度的分布，从而依据钢筋本构计算钢筋应力分布，进而得到沿锚固长度各区间的黏结应力.该试验并未给出s的实测值，但由于应变分布曲线和横坐标包围的面积即s，因此，试验和模型所得应变相同，即应力相等，此亦是判别模型准确性的条件.具体试验细节见文献［30］.

以文献［30］中的两次加载为例验证模型的准确性，所得钢筋应力计算数据和试验结果见图13.由图13 可见，本文所建模型所得应力分布和试验量测的应力基本相同，且应力衰减为零时二者所需黏结长度接近，表明计算应变分布与实测值较好地吻合，证明了所提不均匀冻融损伤黏结滑移模型的准确性.

图13 钢筋应力对比Fig.13 Comparison of reinforcement stress

6 冻融损伤RC剪力墙模型验证

6.1 模型建立

按照前文的建模思路，在纤维模型的基础上依次构建不均匀冻融损伤模型、冻融损伤RC 剪力墙剪切恢复力模型、不均匀冻融损伤黏结滑移模型即可建立本文所提出的冻融损伤RC剪力墙数值模型.

纤维模型中：采用含5 个数值积分点的基于力的非线性梁柱单元；钢筋采用OpenSees 中的SteelMPF 本构；拉压屈服强度取相等值，拉压方向上的应变硬化率均取0.01，曲率参数初始值R0 取15，曲率退化参数CR1、CR2 取推荐值0.925、0.15；非约束混凝土、约束混凝土分别采用Concrete01 与Concrete02 本构，约束混凝土峰值应变ε00，i｛ε00，i=ε0，i×［1+5（Ki-1）］｝和保护层混凝土的峰值应变ε0，i（ε0，i=2fc0，di/Ec0，di）分别由Mander模型和Kent-Park模型计算，并按照不均匀冻融损伤模型对其参数进行折减.具体为：按照大小为10 mm的方形混凝土纤维划分截面，划分示意图见图3.利用不均匀冻融损伤模型对所划分的混凝土纤维进行参数赋值，具体本构参数值列于表2、表3.

表2 不均匀冻融损伤非约束混凝土本构模型参数Tab.2 Constitutive model parameters of nonuniform frost-damaged unconfined concrete（Concrete01）

表3 不均匀冻融损伤约束混凝土本构模型参数Tab.3 Constitutive model parameters of nonuniform frost-damaged confined concrete（Concrete02）

在考虑不均匀冻融损伤纤维截面的基础上通过OpenSees 中Section Aggregator 命令将Hysteretic Material所代表的剪切恢复力模型在截面层次上添加至不均匀冻融损伤纤维截面形成可考虑剪切的不均匀冻融损伤纤维截面.其中：剪切骨架曲线特征点参数按照4.1 节和4.2 节计算方法得到；滞回规则参数列于表4.利用第5 节所建立的不均匀冻融损伤黏结滑移模型所推导的钢筋应力-滑移关系（在OpenSees中具体通过Hysteretic Material 编写）替换不均匀冻融损伤纤维截面中的普通钢筋本构关系（在OpenSees中通过SteelMPF 编写）形成可考虑不均匀黏结滑移和冻融损伤的零长度截面.最终，通过单元调用各截面形成整体剪力墙构件模型.

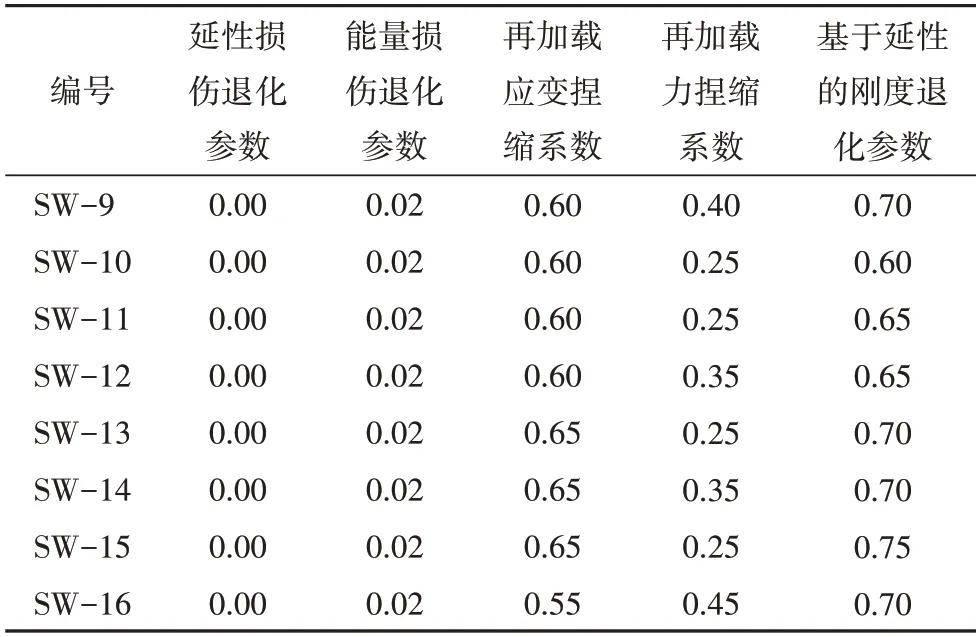
表4 滞回参数Tab.4 Hysteretic parameters

6.2 结果对比

按照上文建模方法建立冻融损伤RC 剪力墙数值模型，并利用Rong等［1］的试验结果作对比，所得对比结果列于图14.由图14 可见：模拟滞回曲线和试验滞回曲线符合良好，其强度衰减、刚度退化、捏缩效应等方面亦吻合较好.相比于试验结果，各模拟结果表现出初始刚度略微偏大，峰值承载力略微偏小的特征.这是因为组合剪切的建模方法引入了对截面刚度的约束使得模拟刚度偏大；与此同时，经过冻融循环作用后，试件冻涨微裂缝使试件初始刚度略微偏小.二者的结合造成了刚度和峰值承载力的微小差异.

图14 滞回曲线对比Fig.14 Comparison of hysteresis curves

此外，数值模型得到的承载能力、变形能力、累积耗能与实测值的误差大小是衡量模型准确度的重要条件.因此，分别取屈服位移误差EΔy、峰值位移误差EΔm、屈服荷载误差Epy、峰值荷载误差Epm、滞回荷载误差Eload以及累积耗能误差Eenergy作为定量化判别数值模型准确性的指标，其对应的计算式参见文献［14］.

依据模拟滞回曲线得到各特征点参数，进而得到数值模型承载能力、变形能力、累积滞回耗能的误差，结果绘制于图15.由图15 可见：屈服荷载误差均值约4%，峰值荷载误差均值约8%，滞回荷载误差均值约9%；屈服位移误差均值约12%，峰值位移误差均值约3%；滞回耗能误差均值约15%.均处于较为精确的范围内.

图15 特征参数误差Fig.15 Error of characteristic parameters

7 结论

本文以冻融损伤不均匀分布为切入点，结合墙顶总变形的组成成分，建立了考虑黏结滑移与剪切效应的不均匀冻融损伤RC 剪力墙数值模型，所得主要结论如下：

1）以ERDM为冻融损伤系数，建立了可考虑由表及里的不均匀冻融渗透的损伤模型.

2）建立了冻融损伤RC 剪力墙构件剪切恢复力模型，并对其准确性进行了验证.

3）构建了不均匀冻融损伤黏结强度模型，同时通过理论推导建立了考虑不均匀黏结应力分布的冻融损伤纵筋滑移模型，并对其进行了验证.

4）结合不均匀冻融损伤模型、冻融损伤剪切恢复力模型、不均匀冻融损伤黏结滑移模型，建立了与实际冻融相吻合的冻融损伤RC 剪力墙数值模型，并利用8 个剪力墙拟静力实测数据对数值模型的准确性进行了验证，结果表明：建立的数值模型可较准确地模拟冻融损伤RC剪力墙低周往复下的力-变形关系，可用于严寒环境下在役RC 剪力墙的抗震性能评估.