基于梁函数-Ritz法的圆柱壳模态特性分析

徐港辉，祝长生

(浙江大学 电气工程学院，浙江 杭州 310027)

圆柱壳作为常见的结构形式，广泛应用于机电、航空航天、船舶舰艇等工程领域.开展圆柱壳的模态特性分析是圆柱壳结构减振降噪的基础，具有重要的理论价值和工程意义.由于壳体振动的复杂性，研究者在不同简化程度的假设下得出多种薄壳理论[1-2].刘彦琦等[3]基于Love理论和Galerkin法分析旋转圆柱壳的模态特性.Qu等[4]基于Reissner理论与区域分解法研究圆柱壳的模态特性和响应特性.Qin等[5]基于Sanders理论对比3种常见的圆柱壳轴向振型容许函数在圆柱壳模态特性分析中的计算精度和效率.Dong等[6]基于Donnell理论讨论面内惯性力对圆柱壳模态特性的影响.尽管Leissa等[1-2,7]对比研究了不同薄壳理论，但是包含不同薄壳理论的统一方法匮乏，导致基于不同薄壳理论的研究结果之间难以比较.

圆柱壳轴向振型函数的精确解含有8个与边界条件相关的待定系数[2]，导致圆柱壳模态特性的精确解析解只在极少数边界条件下(如两端简支)可以求得.因此，基于各种容许函数的圆柱壳模态特性近似解法受到广泛关注.常用的圆柱壳轴向振型容许函数主要有梁函数[3,6-10]、改进的Fourier级数[11-13]、特征正交多项式[14-15]、Chebyshev多项式[4,16-17]及Jacobi多项式[18]等.在这些容许函数中，梁函数属于特殊的一类.由于圆柱壳轴向振型与相同边界条件下梁的弯曲振型较为接近，梁弯曲振型函数(即梁函数)的精确解相对简单，采用梁函数作为圆柱壳轴向振型容许函数具备可行性[1-2].现有研究在采用梁函数开展圆柱壳模态特性分析时，普遍采用单项梁函数直接作为圆柱壳轴向振型函数的方式(本质上与Rayleigh法等价[19])，实际上圆柱壳轴向振型与梁弯曲振型之间不完全相同，导致计算结果的精度有待提升[6,8-9].基于Rayleigh法改进的Ritz法将若干项相互独立的基函数的线性组合用于构造振动系统模态振型的容许函数，能够有效提升Rayleigh法的计算精度[19].在圆柱壳模态特性分析现有文献中，对梁函数-Ritz法的相关研究还较少，梁函数-Ritz法的收敛性和有效性有待进一步分析.Dong等[6]采用单项梁函数法分析不同边界条件下圆柱壳的模态特性，得出梁函数不适用于模拟圆柱壳固支或自由边界条件的结论，这与刘彦琦等[3,7-10]的研究结论存在分歧.

本研究1）以各向同性薄圆柱壳为对象，将梁函数与Ritz法结合，采用有限项不同阶次梁函数的线性组合作为圆柱壳轴向振型容许函数，通过Ritz法推导不同薄壳理论下圆柱壳模态特性分析的统一方法.2）验证不同薄壳理论下梁函数-Ritz法的收敛性与有效性，澄清现有文献中存在的分歧.3）开展参数化分析，研究不同边界条件下长径比与厚径比对圆柱壳模态频率及理论计算精度的影响规律，总结不同薄壳理论的适用范围.

1 统一方法推导

1.1 结构示意图

如图1所示为各向同性薄圆柱壳示意图.圆柱壳的基本结构参数包括中性面半径r、厚度h及轴向长度l.图中xθz为建立在圆柱壳端面中性线上的柱坐标系.圆柱壳中性面上某一点P处沿轴向x、切向θ及径向z方向上的位移分别用u、v及w表示.u、v及w既是空间坐标(x, θ)的函数，也是时间坐标t的函数.

图1 各向同性薄圆柱壳示意图Fig.1 Schematic diagram of isotropic thin cylindrical shell

1.2 圆柱壳的动能与势能

根据板壳理论[1-2]，将各向同性薄圆柱壳对应的动能Ek和势能Ep表示为

式中：及分别为位移u、v及w对时间t的导数；ρ为壳体的密度；σ和ε分别为正应力和正应变，τ和γ分别为切应力和切应变.根据Kirchhoff-Love假设及Hooke定律，各向同性薄圆柱壳的应力与应变满足关系[5]：

式中：Q11=Q22=E/(1-µ2)，Q12=Q21=µQ11，Q66=E/(2+2µ)；E和µ分别为壳体的弹性模量和泊松比.不同类型的薄壳理论对于壳体应变与中性面位移u、v及w的关系的描述不同，其中Donnell理论是最简单的薄壳理论，其对应的应变-中性面位移表达式[6-7]为

常用的薄壳理论还包括Reissner[1-2,4]、Sanders[5,8,16]及Love[3,9-10,13]理论等，它们与Donnell理论之间的对比如表1所示.相比上述4种理论，Flugge理论中εθ和γxθ的表达式更复杂，且势能公式也与式(2)不同，详见文献[18].根据式(2)～(4)及表1，可以将不同薄壳理论下圆柱壳的势能Ep表示为位移u、v及w的函数.

表1 常用薄壳理论对比Tab.1 Comparison of common thin shell theories

1.3 位移函数构造

圆柱壳沿周向具有周期性特征，其周向阶次n＞0的各阶模态均由正弦分量(反对称模态)和余弦分量(对称模态)组成，当周向阶次n=0时，正、余弦分量合二为一[20].现有研究在构造圆柱壳模态位移函数时，通常没有考虑n=0时的情况[5]，对此本研究将做进一步完善.当周向阶次n＞0时，圆柱壳各阶模态的正、余弦分量对应的模态特性相似[20].为了简便，以余弦模态分量为例进行分析.不失一般性，引入无量纲变换ℓ=x/l，此时圆柱壳某一阶模态对应的位移函数表示为

式中：m和n分别为圆柱壳模态的轴向阶次和周向阶次；ω为模态角频率，φ为模态位移的初始相位.无量纲参数ℓ表示相对轴向位置，Um(ℓ)、Vm(ℓ)和Wm(ℓ)为圆柱壳的轴向振型函数.当周向阶次n=0时，圆柱壳的模态振型沿周向不存在波动变化(即与θ坐标无关)，此时圆柱壳各阶模态对应的位移函数表示为

由于圆柱壳轴向振型函数Um(ℓ)、Vm(ℓ)和Wm(ℓ)的精确表达式十分复杂，通常采用满足边界条件的容许函数进行近似.梁函数是常用的容许函数，具有物理意义明确、形式相对简单的优点.现有研究在采用梁函数作为圆柱壳轴向振型容许函数时，通常采取单项梁函数的方式，计算精度较低[6,8-9].本研究将梁函数作为Ritz基函数[19]，采用有限项不同阶次梁函数的线性组合作为圆柱壳轴向振型容许函数，此时有

式中：Xi(ℓ)为与圆柱壳边界条件相同的梁的第i阶弯曲振型函数(梁函数)；I为所用梁函数的项数，X(ℓ)为梁函数组成的1×I维向量，当I=1时，X(ℓ)退化为单项梁函数.ai、bi和ci为待定系数，a、b和c为待定系数组成的I×1维待定向量.以两端固支边界条件为例，梁的第i阶弯曲振型函数为

式中：λi为对应的频率方程cosλmcoshλm=1的解，σi=(coshλi-cosλi)/(sinhλi-sinλi).各种典型边界条件下的梁函数Xi(ℓ)、λi、σi见文献[2]附录I.弹性边界条件下的梁函数Xi(ℓ)、λi、σi较为复杂[21-22]，导致后续积分等运算过程即使借助数值计算也不易实现，本研究暂不讨论.

1.4 基于Ritz法的圆柱壳模态特性分析

Ritz法的基本思想是在采用Ritz基函数构造模态振型的基础上，通过求取振动系统Rayleigh商的驻值解来获得系统的模态频率和模态振型[19].为了定义圆柱壳的Rayleigh商，将式(5)、式(6)分别代入式(1)、(2)，结合式(3)、(4)及表1得到不同薄壳理论下圆柱壳动能与势能的最大值.为了使公式简洁，以下将圆柱壳的轴向振型函数Um(ℓ)、Vm(ℓ)和Wm(ℓ)简写为U、V和W.

1) 当周向阶次n＞0时，有

对于Donnell薄壳理论，Q1=n4W2，Q2=n2WW′′，Q3=4n2W′2.对于Reissner、Sanders和Love薄壳理论，Q1=n4W2+n2V2+2n3VW；Q2=n2WW′′+nVW′′；

Reissner薄壳理论Q3=4n2W′2+V′2+4nV′W′；Sanders薄壳理论Q3=4n2W′2+9V′2/4+6nV′W′+QS；Love薄壳理论Q3=4n2W′2+4V′2+8nV′W′；其中QS=2n2lUW′/r+n2l2U2/(4r2)+3nlUV′/(2r).

2) 当周向阶次n=0时，有

对于Donnell、Reissner、Sanders和Love薄壳理论，Q4分别取0、1/12、3/16和1/3.式(10)、(12)为不同薄壳理论下圆柱壳势能泛函的统一形式，验证了不同薄壳理论之间的差距在h2/r2量级[1-2].

基于Flugge理论也可得到类似式(9)～(12)的结果，并且式(9)～(12)也适用于文献[5]中的3种类型容许函数.本研究采用式(7)所示的梁函数组合作为圆柱壳轴向振型的容许函数.将式(7)代入式(9)～(12)，记q=[aT，bT，cT]T，将圆柱壳动能与势能的最大值整理为矩阵形式：

可以验证：M0=Mn|n=0，K0=Kn|n=0.忽略圆柱壳的阻尼，没有外界激励时，圆柱壳体的机械能守恒，则圆柱壳的最大动能与最大势能应相等.令=，根据式(13)、(14)定义圆柱壳的Rayleigh商[19]为

可以看出，R随待定向量q变化而变化.当R取驻值时，对应的ω即为圆柱壳模态角频率的近似值；将对应的向量q代回式(7)，即可得到圆柱壳模态振型的近似值[19].由R取驻值的条件∂R/∂q=0，得到

模态频率f与模态角频率ω之间满足f=ω/(2π)，由此圆柱壳的模态频率和模态振型求解问题转变为如式(16)所示的矩阵特征值问题.

2 收敛性分析

根据理论推导可知，模态频率的计算结果与表1中所选的薄壳理论以及式(7)中梁函数项数I的取值密切相关.算例圆柱壳参数取自文献[16]：中性面半径r=0.1 m，长度l=0.2 m，厚度h=0.247×10-3m，密度ρ=2 796 kg/m3，弹性模量E=71.02×109N/m2，泊松比µ=0.31.两端固支(C-C)、固支-自由(C-F)及两端简支(S-S)边界条件下，采用表1中4种薄壳理论计算所得的圆柱壳第(1,7)阶模态频率f(1,7)随梁函数项数I的变化曲线如图2所示.可以看出，在C-C和C-F边界条件下，随着项数I的增加，基于各种薄壳理论的模态频率计算结果均逐渐降低并且在项数I为30左右时逐渐收敛.在S-S边界条件下，I对模态频率计算结果的影响很小，基于各种薄壳理论的计算结果在I=1时即达到收敛.进一步对比基于各种薄壳理论的模态频率计算结果可以看出，各种边界条件下基于Reissner、Sanders及Love薄壳理论的计算结果基本相同；基于Donnell薄壳理论的模态频率相对较大，与基于其他3种薄壳的计算结果存在明显的差距，这是Donnell薄壳理论简化程度最大导致的.

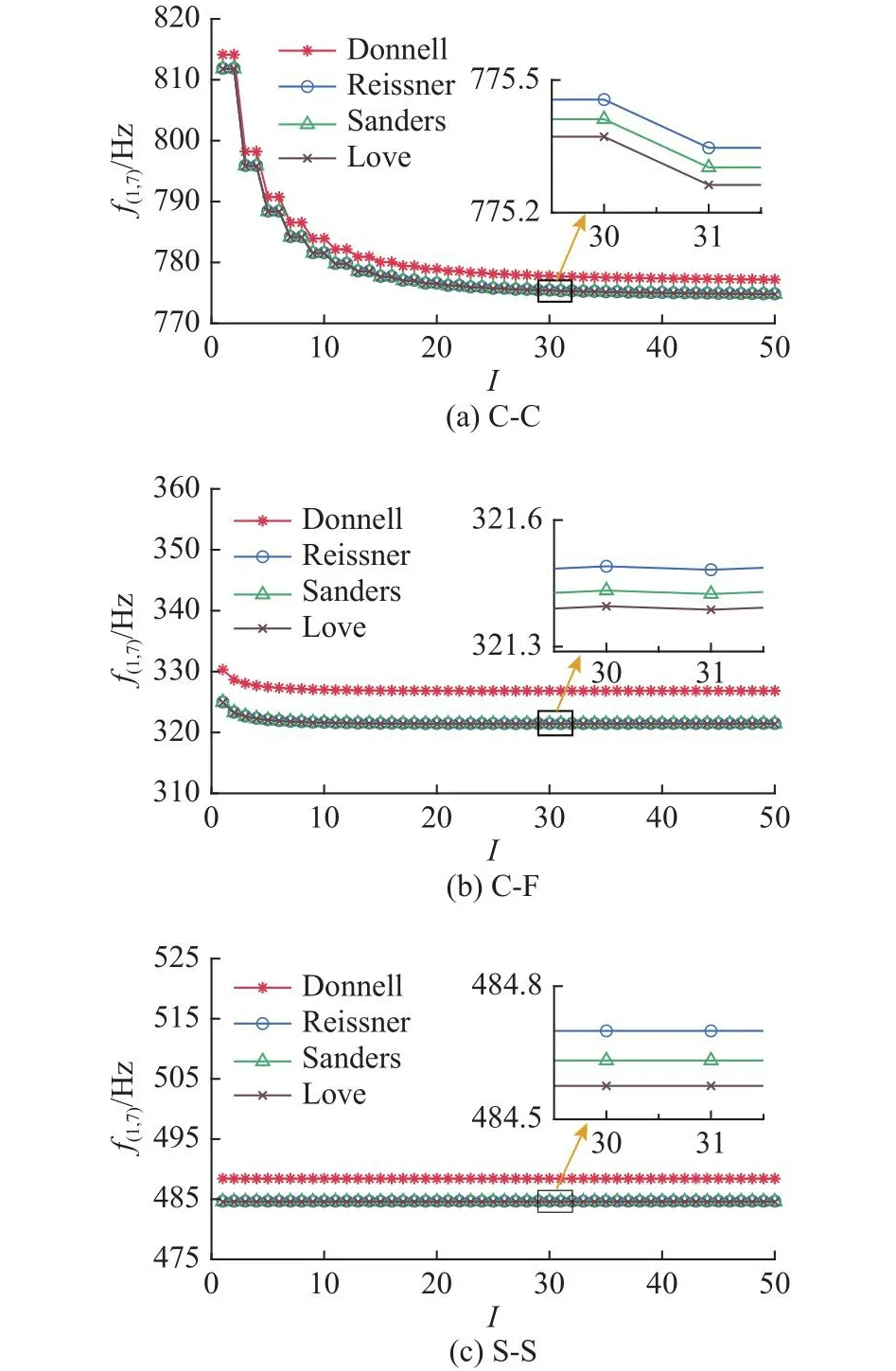
图2 圆柱壳模态频率的理论计算值随项数的变化关系Fig.2 Relationship of theoretical calculated modal frequencies for cylindrical shell with item number

为了定量对比不同边界条件下基于不同薄壳理论的模态频率计算结果的收敛性，在图2的基础上，各种边界条件下不同薄壳理论时均取I=50时的计算结果为基准，得到项数为1～50时基于不同薄壳理论的计算结果的相对误差Δ，如图3所示.可以看出，相同边界条件下基于不同薄壳理论的计算结果的收敛速度差别很小.在3种边界条件中，C-C与S-S理论计算的收敛速度分别为最慢与最快.当I=1时，C-C理论计算的相对误差最大，约为4.8%；当I=5时，Δ=1.8%，其他边界条件对应的相对误差则更小，表明在3种边界条件下基于不同薄壳理论的计算中，采用少数项梁函数就能实现较好的收敛.还可以看出，当I＞30，3种边界条件下理论计算的相对误差已经小于0.1%，此后计算结果的收敛速度逐渐降低，继续增加梁函数项数对模态频率的计算结果影响较小.综合考虑梁函数项数对理论计算收敛误差与收敛速度的影响，在没有特殊说明的情况下，本研究后续理论计算将项数选定为50.

图3 不同边界条件下不同项数理论计算的相对误差Fig.3 Relative errors of theoretical calculations with different item number under different boundary conditions

3 有效性验证

3.1 与单项梁函数法的对比

Dong等[6]基于Donnell薄壳理论，采用单项梁函数作为圆柱壳轴向振型容许函数，计算了不同边界条件下圆柱壳的模态频率(m=1)，得出梁函数不适用于模拟圆柱壳固支或自由边界条件的结论.Dong等[6]采用的圆柱壳参数与本研究的相同，基于该参数和Donnell薄壳理论，通过梁函数-Ritz法得到不同边界条件下圆柱壳的模态频率，并与Dong等[6]的理论结果及本研究有限元法(finite element method, FEM)的仿真结果进行对比，如表2所示.表中，n为模态的周向阶次，fC-C、fC-F和fS-S分别为两端固支、固支-自由和两端简支边界条件下圆柱壳的模态频率.有限元法基于有限元软件Ansys实现.其中网格划分采用Solid186实体单元，该单元对应的壳体理论为三维弹性理论，比各种薄壳理论更准确，因此有限元法结果可以作为理论计算结果的对比依据.可以看出，当I=1时，本研究模态频率的计算结果不仅与文献[6]的几乎相同，且与有限元法结果的一致性较好，由此验证了本研究理论推导和计算结果的正确性.观察fC-F，当I=1时，本研究模态频率的计算结果与有限元法结果的差距未超过合理范围，但与文献[6]的诸多数据差距非常大，表明文献[6]的数据可能存在问题.这些问题不是采用梁函数作为容许函数导致的，因此Dong等[6]得出的梁函数不适用于模拟圆柱壳固支或自由边界条件的结论不合理.当I=50时，以有限元法结果为基准观察fC-C、fC-F可以看出，本研究模态频率的计算精度相比I=1时具有明显提升，进一步验证了本研究数据的合理性，也验证了梁函数-Ritz法的有效性.观察fS-S可以看出，I=50时的结果与I=1时的完全相同，这与第2节所示的收敛性规律一致.

表2 3种边界条件下的圆柱壳模态频率对比(梁函数)Tab.2 Comparison of modal frequencies for cylindrical shell at three boundary conditions (with beam functions)

3.2 与不同类型容许函数方法的对比

Qin等[5]基于Sanders薄壳理论，采用改进的Fourier级数(MF)、特征正交多项式(OP)和Chebyshev多项式(CP)作为圆柱壳轴向振型容许函数，验证3种容许函数在圆柱壳模态频率计算方面均具有较高的精度.文献[5]算例中采用的圆柱壳参数与本研究的相同，并且将3种容许函数的项数统一设为25.为了进一步验证本研究所提方法的有效性，基于该圆柱壳参数和Sanders薄壳理论，令梁函数项数为25，通过梁函数-Ritz法计算不同边界条件下圆柱壳的模态频率，并与文献[5]的理论结果进行对比，如表3、4所示.可以看出，本研究模态频率的计算结果与文献[5]采用3种类型容许函数得到的结果具有较好的一致性，进一步验证了本研究所提方法的有效性.将表2分别与表3、4对比可以发现，相对于有限元法的结果，采用Sanders薄壳理论得到的计算结果(I=25)比采用Donnell薄壳理论时的(I=50)精度更高，验证了Donnell薄壳理论的计算误差较大，这与图2所示的规律相符.

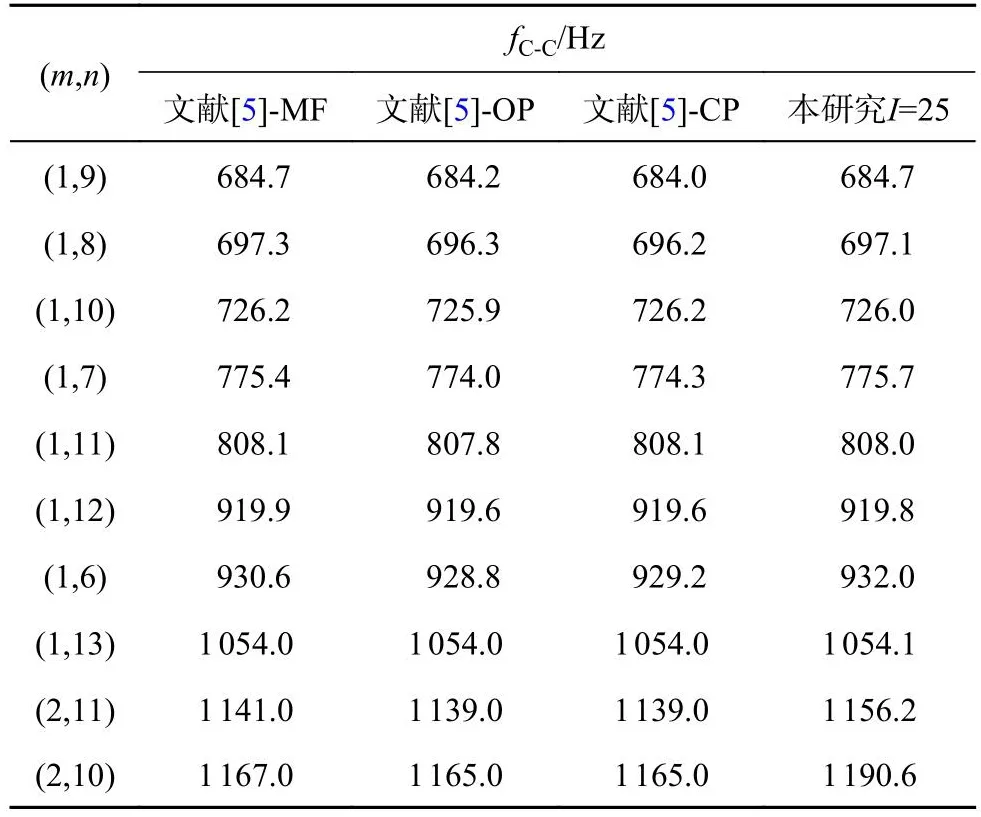
表3 两端固支圆柱壳模态频率对比(不同类型容许函数)Tab.3 Comparison of modal frequencies for cylindrical shell clamped at both ends (with different types of admissible functions)

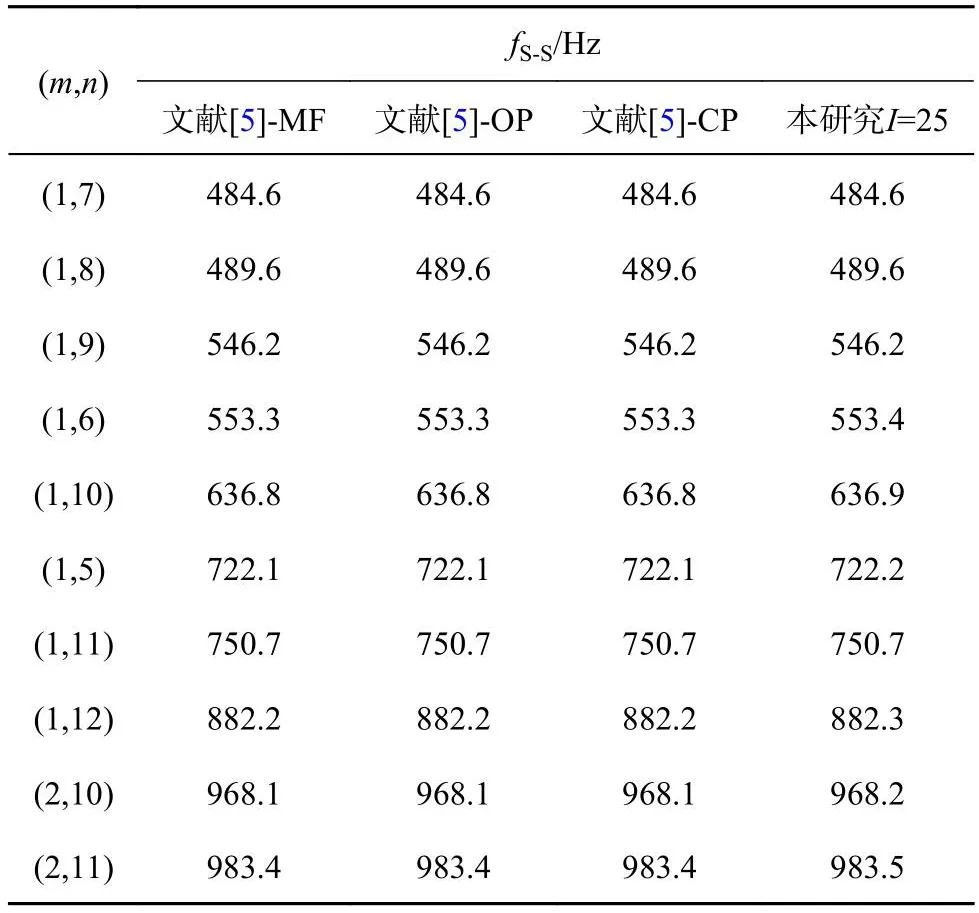
表4 两端简支圆柱壳模态频率对比(不同类型容许函数)Tab.4 Comparison of modal frequencies for cylindrical shell simply supported at both ends (with different types of admissible functions)

3.3 圆柱壳与梁的模态振型对比

相同边界条件下圆柱壳轴向振型与梁弯曲振型相近，两者的具体差别在现有研究中涉及较少.本研究采用Sanders薄壳理论得到不同边界条件下圆柱壳前4阶轴向振型(取I=50)，并将结果与梁弯曲振型(取I=1)以及有限元法得到的壳体轴向振型进行对比，结果如图4所示.可以看出，在两端固支(C-C)和固支-自由(C-F)边界条件下，圆柱壳轴向振型与梁弯曲振型具有相似的波动特征，但两者的波峰、波谷以及节点的相对轴向位置并不完全相同，这也是采用单项梁函数法计算非两端简支圆柱壳模态特性时存在误差的原因.两端简支(S-S)边界条件下的圆柱壳轴向振型与梁弯曲振型完全重合.实际上，两端简支圆柱壳体轴向振型函数的8个待定系数中只有1个待定系数不等于零，其化简结果与两端简支梁的振型函数完全相同[2]，图4(c)与此相符，一方面验证了本研究所提方法的有效性，另一方面也解释了图2(c)与表2中fS-S在I=1时就达到收敛状态的原因.图4中有限元法结果也验证了理论计算和分析的正确性.

图4 圆柱壳轴向振型(I=50, FEM)与梁弯曲振型(I=1)对比Fig.4 Comparation of axial modal shapes for cylindrical shells(I=50, FEM) and bending modal shapes for beams (I=1)

4 参数影响分析

长径比与厚径比是圆柱壳的关键结构参数，令圆柱壳的长径比l/r分别为1、2、3、4、5，令厚径比h/r分别为0.05、0.10、0.15、0.20，参数影响分析中的厚径比远大于收敛性分析中的厚径比(约为0.002 5).经过验证，此时各长径比与厚径比下圆柱壳低阶模态频率主要分布在m=1，n=2～4阶次附近，因此选取壳体第(1,4)阶模态频率为例进行研究.

由于长径比与厚径比对圆柱壳模态频率的大小有影响，对理论计算的精度也有影响.经过验证，基于表1中不同薄壳理论的模态频率计算结果与有限元法结果的变化规律相一致，只是在幅值上存在差异.如图5所示为有限元法结果，可以看出，3种边界条件下长径比的减小或者厚径比的增大均可以使圆柱壳模态频率f增大，但是壳体模态频率对长径比与厚径比变化的敏感程度存在差异.当厚径比为0.05～0.20时，壳体模态频率对厚径比的变化始终较为敏感；当长径比小于2时，圆柱壳模态频率对长径比的变化比较敏感，但当长径比大于2时，圆柱壳模态频率随长径比变化而变化的趋势明显放缓.如图5(b)所示，在固支-自由边界条件下，当长径比大于2时，圆柱壳第(1,4)阶模态频率基本上不随长径比的变化而产生变化.因此，在设计或加工圆柱壳结构过程中，有必要对圆柱壳的厚度尺寸予以特别关注.图5中有限元法也采用Solid186实体单元进行网格划分，该单元对应的壳体理论为三维弹性理论，因此对应的结果可以作为理论计算结果的对比依据.

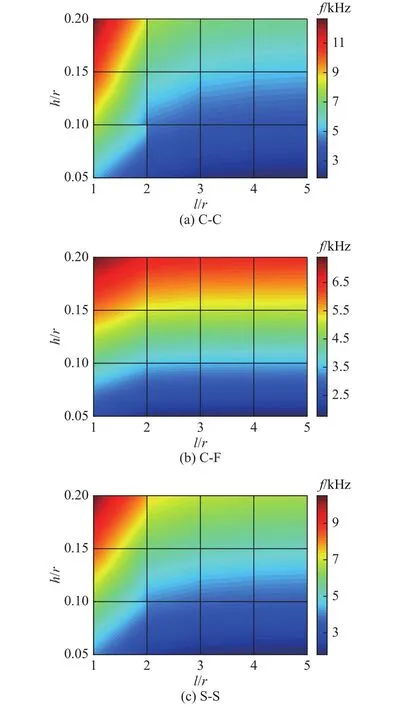
图5 不同长径比与厚径比时圆柱壳模态频率的分布Fig.5 Modal frequencies distribution of cylindrical shells with different length-to-radius and thickness-to-radius ratios

以图5为基准，得到3种边界条件下不同长径比与不同厚径比时基于不同薄壳理论的模态频率计算误差δ的分布，如图6所示.可以看出，在不同边界条件、不同长径比以及不同厚径比下，基于Donnell理论的模态频率计算误差始终明显高于基于其他3种薄壳理论的，其中Love理论的计算精度最高，Reissner和Sanders理论与Love理论的计算精度相接近.各薄壳理论的计算精度与长径比和厚径比均有关系，相对长径比的变化，各薄壳理论的计算精度对厚径比的变化更为敏感.当厚径比增大时，各薄壳理论的计算误差始终明显增大.当长径比增大时，虽然大部分情况下各薄壳理论的计算误差均有所减小，但是当l/r≥2时，这种影响变得并不显著.通过进一步的定量分析可知，当h/r≤0.1时，各种情况下基于Donnell理论的模态频率计算误差均未超过11%，基于其他3种理论的模态频率计算误差均小于8%，因此表1中的4种薄壳理论基本均能满足工程应用需求.当0.1＜h/r≤0.15时，基于Donnell理论的计算误差波动范围较大(7.3%～18.6%)，基于其他3种理论的计算误差在l/r≥2时均不超过8%，因而此时这3种理论适用于l/r≥2的圆柱壳振动分析.当厚径比继续增大到0.2时，各种长径比下基于Donnell理论的模态频率计算误差均大于16.9%，难以满足工程应用需求，基于其他3种理论的计算误差在l/r≥3时仍小于10.5%，因此这3种理论仍然能够满足工程应用需求.综上所述，Donnell理论主要适用于h/r≤0.1的圆柱壳振动分析，Reissner、Sanders和Love理论不仅适用于h/r≤0.1的圆柱壳振动分析，还可以有条件地应用于0.1＜h/r≤0.2的圆柱壳振动分析.

图6 不同长径比与厚径比时理论计算结果的误差分布Fig.6 Error distribution of theoretical calculation results for different length-to-radius and thickness-to-radius ratios

5 结 论

（1）将梁函数与Ritz法相结合，采用有限项不同阶次梁函数的线性组合作为圆柱壳轴向振型的容许函数，建立包含不同薄壳理论的圆柱壳模态特性分析统一方法，厘清了不同薄壳理论之间的关联，为基于不同薄壳理论分析结果的对比提供了理论支持.

（2）梁函数适用于模拟圆柱壳固支或自由边界条件，文献[6]结论中关于梁函数适用性的描述是不合理的.将梁函数与Ritz法相结合，可以进一步提升梁函数在圆柱壳模态特性分析时的计算精度.

（3）在两端固支、固支-自由及两端简支3种边界条件下，减小长径比或者增大厚径比均可以使圆柱壳模态频率增大.随着长径比的减小或者厚径比的增大，基于不同薄壳理论的模态频率计算结果的相对误差呈现增大趋势.

（4）基于Reissner、Sanders以及Love理论的模态频率计算误差相接近，其中Love理论的计算精度最高，Donnell理论的计算精度明显低于这3种理论.Donnell理论主要适用于厚径比不超过0.1的圆柱壳振动分析，Reissner、Sanders和Love理论可以有条件地应用于厚径比为0.2的圆柱壳振动分析，适用范围比Donnell理论更广.

（5）本研究的工作均在典型边界条件下进行，后续研究可以考虑弹性边界条件下圆柱壳模态分析中梁函数的应用问题.