H.266/VVC二维变换的统一硬件结构

陈俊煜，孙斌，黄晓峰，盛庆华，赖昌材，金心宇

(1.浙江大学 工程师学院，浙江 杭州 310015；2.杭州电子科技大学 通信工程学院，浙江 杭州 310018；3.杭州电子科技大学 电子信息学院，浙江 杭州 310018)

新一代国际视频编码标准通用视频编码(versatile video coding, VVC)[1]相比前一代的高效视频编码(high efficiency video coding, HEVC)[2]，在编码效率上提高了大约1倍[3]，计算复杂度也大幅度提高[4].变换编码是视频编解码的关键部分[5].可以从以下3个方面概括VVC与变换相关的特性[6].1）VVC总共有3种变换类型：DCT-II、DSTVII和DCT-VIII.相比于HEVC，VVC将最大变换尺寸扩展到64，采用变换尺寸为4、8、16、32、64的DCT-II和变换尺寸为4、8、16、32的DSTVII、DCT-VIII.VVC引入多变换核选择技术(multiple transform selection, MTS)控制变换类型.2）VVC的高频置零技术减少了大尺寸变换块的计算量和存储空间.当采用DCT-II时，长或宽为64的大尺寸变换块在高频置零后，只保持低频32×32的有效数据；当采用DST-VII或DCTVIII时，长或宽为32的大尺寸变换块在高频置零后，只保持低频16×16的有效数据.3）VVC的多类型树划分技术(multiple type tree, MTT)会产生非对称变换块.VVC在水平和垂直方向上可以采取不同的变换类型和尺寸.

研究者提出许多关于变换部分的硬件结构.在VVC编码标准方面，1）Garrido等[7-9]基于通用乘法器提出二维变换的流水线结构，将双端口静态随机存取存储器(static random-access memory,SRAM)排列成矩阵形式实现转置存储，利用先入先出队列(first input first output, FIFO)缓存块信息.Garrido等[7-9]使用的转置存储器占用面积较大.2）Fan等[10]提出的支持混合块处理的DST-VII、DCT-VIII变换结构，主要基于RAG-n(n-dimensional reduced adder graph)算法[11]优化后的多常量乘法(multiple constant multiplication, MCM)实现，在转置存储器的流水线结构设计上采用对角存储和乒乓读写方式.Fan等[10]没有实现DCT-II，也没有结合高频置零优化转置存储器.3）Farhat等[12-13]基于通用乘法器提出轻量级的变换结构，虽然实现VVC所有的变换类型和尺寸，但不支持流水线处理，导致结构的吞吐率低.4）Mert等[14]提出可重构的数据路径，具有比传统使用分离的数据路径更小的面积.5）Hao等[15-16]在转置存储器的设计中使用统一的数据映射方案，针对一维变换提出矩阵分解算法来减小面积.在HEVC编码标准方面，Meher等[17]提出尺寸复用结构，大尺寸变换可以复用小尺寸变换从而提高资源利用率；Zheng等[18]提出可重构的蝶形变换结构，解决了传统结构在运算小块时大块计算资源闲置的问题.

本研究主要实现VVC的DCT-II、DST-VII、DCT-VIII变换类型.1）基于32个并行度实现全流水结构，支持混合块的输入.2）基于Hcub(heuristic cumulative benefit)算法[19]优化后的MCM设计统一的结构来实现不同变换类型和尺寸.3）在转置存储器的设计中引入读写指针，取代传统的乒乓读写方案；采用对角线式存储结构，并设计统一的数据映射方案.4）利用VVC变换过程中高频置零的特性优化SRAM存储空间，以FIFO取代传统的寄存器缓存块信息.

1 二维变换的流水线结构

1.1 VVC中的二维变换

DCT-II、DST-VII和DCT-VIII变换矩阵的数学定义式为

式中：T(i,j)为变换矩阵元素值;i为行索引，j为列索引，N为变换尺寸；i,j=0,1,···,N-1.对于所有的变换类型，N点一维变换的矩阵形式为

式中：X为像素残差矩阵，TN为N点变换矩阵，Y1D为一维变换系数矩阵.任何像素块二维变换的计算式为

式中：XM×N为宽度为M、高度为N的像素残差矩阵，TM、TN分别为M、N点的变换矩阵，Y2D为二维变换系数矩阵.

直接进行变换操作涉及浮点数运算，浮点数的计算复杂度较高；在数字化处理过程中，舍入误差不可避免，将导致编/解码端出现失配的问题，因此从高级视频编码(advanced video coding,AVC)开始，采用整数变换.相比于浮点变换矩阵，整数变换的变换矩阵做了整数化处理，VVC对N点变换矩阵的每个元素标量数乘一个较大的放大因子进行整数化，从而在整数化过程中减小计算精度的损失.整数化后的矩阵仍然保持原本可以使用蝶形快速算法的规律.整数变换过程的表达式为

式中：E(N)为N点变换矩阵的放大因子，、分别为M、N点的整数变换矩阵，Yint为二维整数变换系数矩阵.

1.2 二维变换的流水线结构

如图1所示，本研究所提二维变换流水线结构主要由3个部分组成：一维行变换模块、转置存储器、一维列变换模块，系统的并行度为每时钟周期32个像素.一维行变换的输入数据是预测得到的像素残差，输入位宽为9位，输出位宽为16位，一维行变换得到的块数据和块信息（宽、高、类型等）将分别存入由SRAM实现的转置存储器中.完成整个矩阵的存储后，数据和相应的信息会流入一维列变换，一维列变换的内部结构与一维行变换几乎一致，只是输入、输出位宽都为16位.

图1 二维变换的流水线结构Fig.1 Pipelined architecture of 2D transform

由于转置存储器处理非对称小像素块时读写速率不匹配，产生数据写入碰撞问题，须将小块的多行向量拼凑到同一并行度，使得读写速率匹配，进而实现流水线处理.以8×32的像素块为例，其高度为8、宽度为32，若单周期只处理1个向量，则输入到一维行变换需要8个周期，即写入转置存储器需要8个周期，输入到一维列变换需要32个周期，即从转置存储器中读出需要32个周期.由于写入时间小于读出时间，导致存储器堵塞，在转置存储器存满后就会造成写入碰撞.将小块的输入拼凑到32个并行度，同时处理多个尺寸小于32的向量（8组大小为4的向量，4组大小为8的向量，2组大小为16的向量），就可以使写入和读出时间相同.由于64×64的像素块存在高频置零，读出时间短于写入时间，不会造成流水的堵塞.

2 一维变换的统一结构

2.1 VVC中的一维变换

DCT-II可以使用Chen等[20]提出的蝶形快速算法进行计算，使计算量大大减少.如图2所示，DCT-II8代表大小为8的变换矩阵，DCT-II4代表大小为4的变换矩阵，特点是1)偶数行偶对称，奇数行奇对称（首行是第0行）；2) 4×4的变换矩阵由8×8矩阵的偶数行的前一半元素组成.其他尺寸的变换矩阵也有这2个特点，因此可以设计基于蝶形快速算法的统一计算结构.

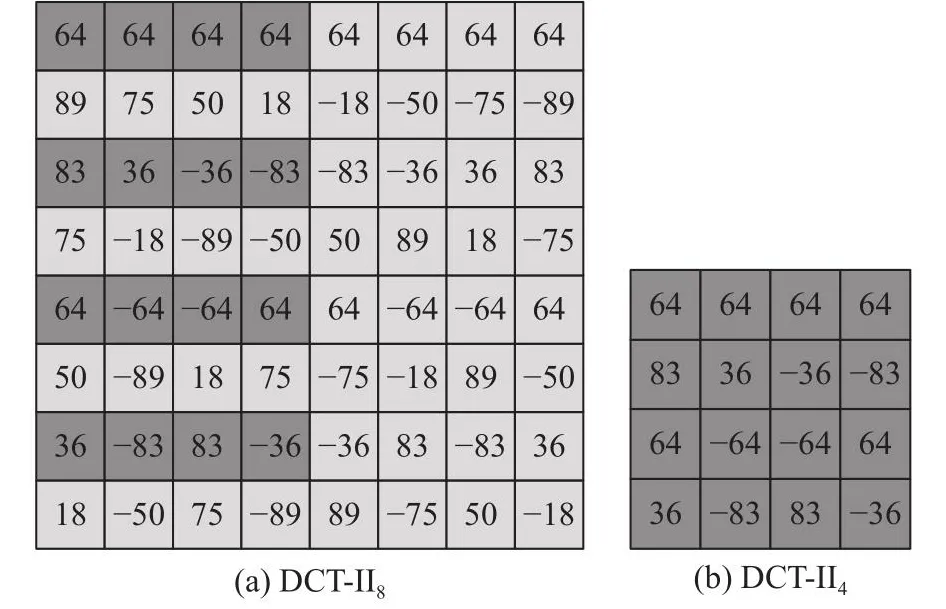
图2 DCT-II的2种变换矩阵Fig.2 Two tgpes of transformation matrices for DCT-II

DST-VII和DCT-VIII没有与DCT-II相同的蝶形特性，即便VTM (VVC 测试模型)为DST-VII和DCT-VIII提供快速算法，这样的快速算法也难以用统一的结构实现.DST-VII、DCT-VIII的变换矩阵在数值上具有偶数行反序，奇数行反序且反号的特点（首行是第0行）.如图3所示，DST-VII4和DCT-VIII4分别代表大小为4的2种变换矩阵，二者可以共享1套计算资源，只要在输入输出端分别采用1组选择器简单处理输入输出数据即可实现2种变换类型.

图3 DST-VII4与DCT-VIII4的变换关系Fig.3 Relationship between DST-VII4 and DCT-VIII4

2.2 一维变换的统一结构

本研究所提一维变换结构基于MCM的方法实现.MCM优化问题将给定的1组常数生成仅用加法、减法和移位组成的常量乘法器块，用以与输入变量进行相乘运算，并通过算法来减少加法器、减法器、移位器的使用.在硬件设计中，加法器/减法器所需资源远远大于移位器，因此如何减少加法器/减法器的个数是硬件优化的关键.Hcub算法[19]的提出正是为了减少加法器/减法器的个数，寻找解决MCM问题的最优解.在文献[19]中,该算法找到的解决方案所需加法和减法数量比RAG-n算法少20%.当常量个数和位宽不断变大时，Hcub算法的优势会更加明显，其对中间计算结果的复用性更高.基于MCM实现的一维变换结构如图4所示.由于系统的并行度为每周期32个像素，最大块的尺寸为64，为了能够在后级使用蝶形快速算法减少计算量，在模块的输入级加入串转并模块，将尺寸为64的2个周期输入数据合为1个周期.由于存在高频置零，一维变换最大输出32个有效数据，因此无需在输出端进行处理.

图4 基于MCM的一维变换统一结构Fig.4 Unified architecture of 1D transform based on MCM

DCT-II可以采用蝶形快速算法进行计算的特性，大大降低了乘法和加法操作的个数，减少了后级MCM和加法树中的资源消耗，DST-VII/DCT-VIII没有相同的特性，采用直接计算的方法.如图5所示的蝶形运算模块用于对变换类型为DCT-II的输入数据生成蝶形运算单元，对DST-VII、DCT-VIII的输入数据仅进行延时操作.图中，x为经过串转并模块后的向量，a为N点蝶形模块的输入向量，b为输出向量，MUX为多路复用器，蝶形变换的输入输出关系为

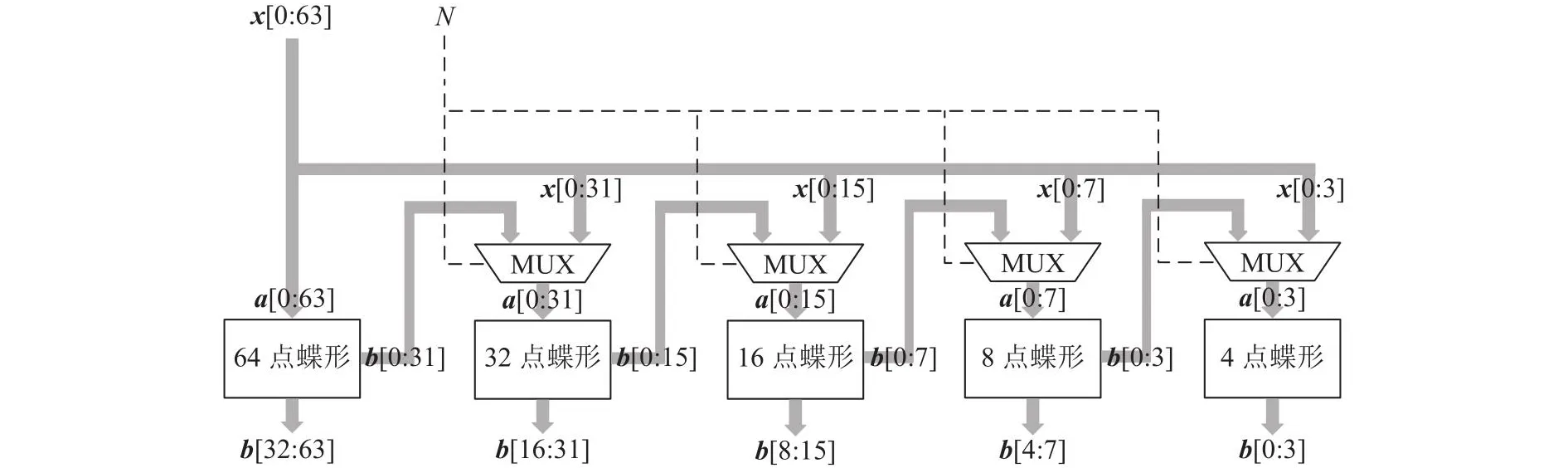
图5 蝶形运算结构Fig.5 Butterfly architecture

大尺寸的蝶形变换可以调用小尺寸的蝶形变换，从而提高资源利用率.小块的多行向量须拼凑到同一并行度才能实现读写速率的匹配，因此例化2个16点蝶形模块、4个8点蝶形模块和8个4点蝶形模块，在总体上实现32个并行度下的流水线结构.

如图6所示，DST-VII和DCT-VIII可以共享1套计算资源，默认输入下输出为DST-VII的系数结果，若当前变换类型为DCT-VIII，则通过选择器将输入数据反序，输出数据在奇数行添负号，得到系数结果.图中，DMUX为分路器.

图6 DST-VII和DCT-VIII的统一结构Fig.6 Unified architecture of DST-VII and DCT-VIII

基于MCM方法的结构是设计多组移位加法单元(shift-addition unit, SAU)作为常量乘法的运算单元.通过需要运算的变换系数得到所有可能与某个输入数据相乘的常量，根据Hcub算法生成对应的SAU.本研究采用统一的计算结构，即生成的计算单元可以供所有的变换类型和变换尺寸使用.这样的结构可以最大化地复用中间计算结果，也可以复用后级加法树的资源，在最大程度上共享资源并降低功耗.在MCM的计算模块中，输入总共有64个数据，这64个输入数据来自不同的数据路径，因此可以根据所需要的变换矩阵系数为输入数据设计相应的SAU.如图7所示为不同输入数据对应的SAU.图中，c为输入数据，其中SAUc[0:1]和SAUc[2:3]共同处理来自第1个4点蝶形模块的数据，SAUc[4:5]和SAUc[6:7]共同处理来自第2个4点蝶形模块或第1个8点蝶形模块的数据.例如，变换类型为DCT-II且尺寸为8，有效输入数据为c[0:31]，该输入数据包含4组尺寸为8的输入向量，分别由SAUc[0:7]、SAUc[8:15]、SAUc[16:23]、SAUc[24:31]处理.DST-VII/DCT-VIII与尺寸为64的DCT-II共同对应的有效输入数据为c[32:63]，c[32:63]对应的常量乘法放在SAUc[32:63]中生成.这样的MCM计算模块发挥了利用多常量乘法进行优化的特点，常量越多，可以共用的中间计算单元也越多，因此功耗降低且逻辑资源的使用减少.经过MCM的计算后，根据当前变换的类型和大小对SAU输出的结果进行选择，并输入加法树模块对数据进行累加求和.为了提高整体的时序，减少组合逻辑关键路径的长度，整个加法树划分为3级.应限制一维变换的结果不超过16位，因此从加法树模块得到的数据须右移缩放，输出的即为一维变换后的结果.

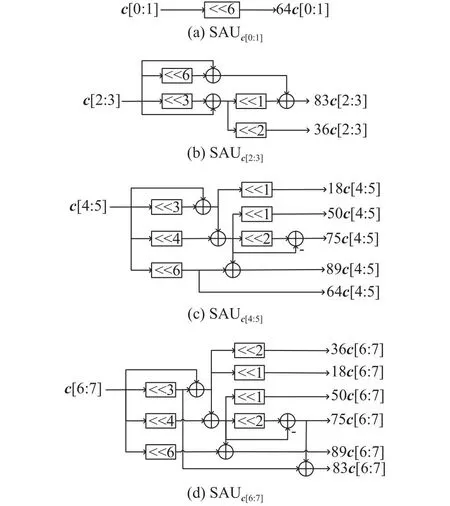
图7 不同输入数据对应的移位加法单元Fig.7 Shift-addition units for different input data

3 转置存储器

实现二维变换的流水线结构须存储一维行变换的结果，待完成1个矩阵的计算后再开始一维列变换，为此须设计满足流水线处理要求的转置存储器.如图8所示，本研究提出的转置存储器基于双口SRAM实现，使用对角线存储方案并设计统一的数据映射方案，同时配合读写指针进行操作，利用FIFO来缓存块信息.图中，y1为一维行变换输出数据，y2为转置存储器输出数据.双口SRAM由32块存储体(Bank)组成，由此实现32个数据的并入、并出.经过高频置零优化后的转置存储器深度计算式为

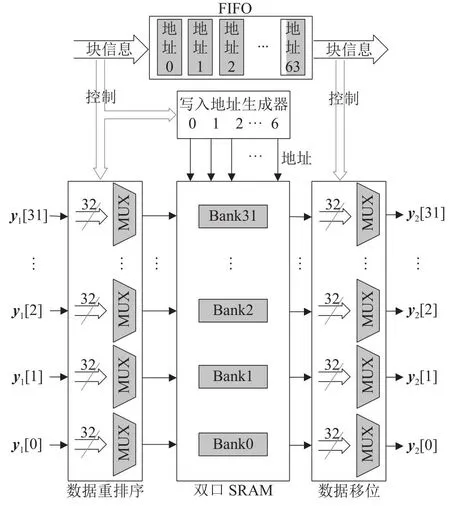
图8 转置存储器结构Fig.8 Transpose memory architecture

式中：VY为一维行变换后最大输出块的有效数据个数，H为系统的并行度，D为每个存储体的深度.VVC中最大的变换块为64×64，但其具有高频置零的特性，在一维行变换后输出的最大有效块数据个数为64×32个.系统的并行度为32，因此可以计算出每个Bank的深度为128，需要7根地址线.图8中的FIFO用来缓存包括变换尺寸、变换类型在内的块信息.由于最大块的读出需要64个周期，FIFO的深度不超过读时钟的最大值，本研究中的FIFO深度为64.

为了实现数据的并入并出，考虑到SRAM在1个时钟内只能在1个特定地址读写的特性，本研究在存储上采用对角存储的方案.实现思路为将32个并行数据经过移位操作后斜向写入不同存储体的不同地址内，在读取时只需对存储在不同存储体同个地址的数据进行移位后便可获得转置后的向量.以4×32的输入矩阵为例，该矩阵是一维行变换的输出结果，如图9(a)所示，数字0～31代表每周期处理的32个数据，不同的灰度色彩代表不同的周期，该矩阵须分4个周期进行存储.由于在读操作开始的时候，要在1个时钟内读出输入矩阵1列所有的数据，并进行多向量的拼凑，转置存储器存储结构的设计如图9(b)所示.其中32个并行数据被对角写入不同存储体中，读出时按照地址顺序依次读出并进行移位操作即可.为了避免读写碰撞的产生，在转置存储器结构上加入读写指针，写指针指向一维变换中的向量存储的地址，读指针指向转置存储完毕的上一个矩阵的起始地址.

图9 输入矩阵与存储结构Fig.9 Input matrix and storage structure

由于存在高频置零，转置存储器的延迟(latency)是不固定的.对非64×64的变换块来说，1个完整变换块的读写周期均不超过64个时钟；当64×64的变换块进入时，高频置零使得1个完整变换块的写入周期为128个时钟，读出周期只需64个时钟.为了确保读写不发生碰撞，当64×64的变换块进入时，读出操作须等待64个时钟才能进行.若64×64的变换块后续读出的为非64×64的变换块时，可以直接进行读出操作，从而缩短小块的延迟.如图10所示，在1个完整的二维变换过程中，非64×64的变换块的延迟为81个时钟周期，64×64的变换块的延迟为145个时钟周期.

图10 二维变换流水线结构时序图Fig.10 Timing diagram of pipelined 2D transform architecture

4 实验结果与分析

使用Verilog HDL实现提出的结构，并使用Design Compiler在UMC 28 nm工艺库下进行综合实现.综合实现的总面积为0.669 759 mm2(SRAM的面积为0.052 924 mm2，逻辑资源的面积为0.616 835 mm2).为了进行不同工艺下的面积对比，将逻辑资源的面积换算成等效逻辑门的数量(本实验综合环境下单位逻辑门的面积为0.55 µm2)，换算后的等效逻辑门数量(gate count，GC)计算式为

综合得到的最大频率为724 MHz，功耗为48.2 mW.作为对比，本研究同时实现分离MCM结构，该结构在Fan等[10]研究的基础上增加DCT-II变换类型，将DCT-II与DST-VII/DCT-VIII变换核分离实现，并将最大尺寸扩展到64，同样采用所提转置存储器，将时钟频率约束在724 MHz，在同一环境下进行综合.综合得到的NGC=1 135.7 ×103，功耗为95.4 mW.可见，相比分离的MCM计算结构，本研究的统一结构在同条件下可以减少1.3%的面积和49.5%的功耗.因为统一的计算结构可以发挥MCM的优势，最大化的共享中间计算结果，并且共享一部分寄存器，所以在功耗上得到比较大的改善；又因为统一结构需要额外生成一些选择逻辑，所以在面积上的改善并不明显.

如表1所示为基于ASIC设计的关键参数，将本研究的实验结果与其他相关文献的实验结果进行比对，包括HEVC标准和VVC标准的相关研究成果.表中，F为最大频率，H为该系统的并行度，P为功耗.文献[10]实现DST-VII/DCT-VIII变换核，得出结论：基于MCM实现的结构相比直接使用乘法器的结构在面积上节省了11.4%，在功耗上节省了9.9%.在相同并行度下，本研究的NGC是文献[10]的2.26倍，原因是文献[10]没有实现最大尺寸为64的DCT-II变换核，DCT-II变换核的面积大约为DST-VII/DCT-VIII变换核的1.30倍，因此文献[10]的面积与本研究对照实现的分离MCM结构基本一致.本研究实现的统一结构在功耗上得到比较大的改善.文献[13]与本研究都实现了3种变换类型，Farhat等[13]提出的结构基于通用乘法器实现，文献[13]的计算逻辑是根据不同的变换类型和尺寸来选择送入乘法器的变换矩阵与输入数据进行计算.文献[13]的并行度为1 像素/周期，资源的利用率很高，面积也较小.从吞吐率的角度分析，文献[13]不支持流水线处理，因此在吞吐率上低于本研究.在28 nm的工艺下，本研究实现结构的最大频率高于文献[13].文献[14]同样实现3种变换类型并改进传统MCM的结构，通过选择器对MCM结构进行重配置从而复用部分计算资源.文献[14]没有实现最大尺寸为64的变换块，且在并行度为8 像素/周期的前提下实现面积仅略低于文献[10].文献[17]、[21]的实验结果基于HEVC得出.Meher等[17]提出的DCT-II变换核是尺寸复用的蝶形结构，本研究对于DCT-II变换核的实现也采用这样的方法，并结合DST-VII/DCT-VIII变换核的特性进行统一设计.Shabani等[21]提出的一维变化结构改进传统MCM方法，采用Muxed-MCM结构，生成的SAU具有一定的可重用性和可扩展性，但该结构随着常量的增加难以通过算法进行优化.

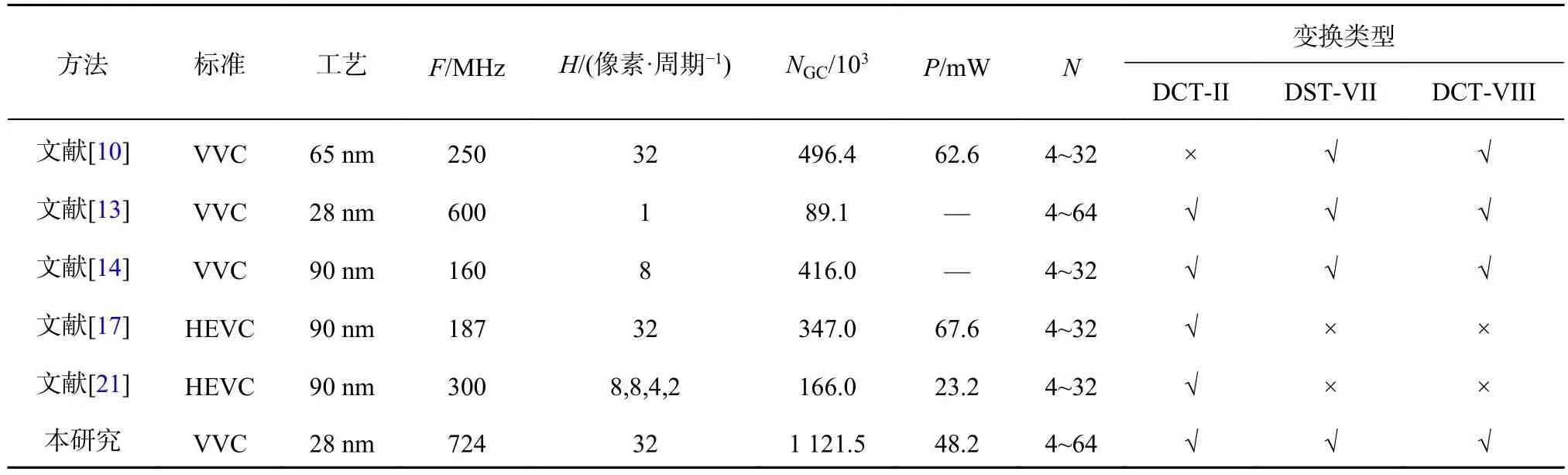
表1 基于ASIC实现的二维变换硬件设计对比Tab.1 Comparison of 2D transform hardware designs based on ASIC

转置存储器硬件设计的对比如表2所示.表中，NB为存储体个数，D为每个存储体的深度，W为每个存储体的位宽.本研究所提转置存储器结构基于双口SRAM实现.Garrido等[8]提出的结构将转置存储器排列成1个矩阵的形式，在4个并行度下使用16个存储体，本研究所提结构采用对角线式的存储结构实现并入、并出，使用4个存储体就可以实现4个并行度的设计.文献[8]没有对高频置零进行优化，按照本研究设计方法深度为256.Fan等[10]提出的转置存储器结构基于乒乓读写的方式实现，该结构将32×32的矩阵组成1组输入实现流水.DST-VII、DCT-VIII中大小为32的变换存在高频置零，实际上最大的中间结果只有32×16个有效数据，因此采用本研究所提读写指针的方式根据式(5)计算深度为32即可实现流水.

表2 转置存储器硬件设计对比Tab.2 Comparison of transpose memory hardware designs

5 结 语

本研究提出统一的二维变换硬件结构，支持VVC的DCT-II、DST-VII、DCT-VIII变换类型以及所有大小的变换尺寸.该结构基于Hcub算法优化后的MCM实现，对所有变换类型和尺寸设计共用的MCM计算单元，相比直接使用乘法器的方案和使用分离的MCM计算结构的方案可以节省面积和功耗.在二维变换的流水线设计上，基于32个并行度实现全流水结构，设计支持流水线处理的转置存储器，支持混合块的流水输入，结合高频置零对转置存储器的大小与处理时间进行优化，在一定的初始延时后每个周期都会得到32个变换结果.对于整个二维变换而言，非64×64的变换块的延迟为81个时钟周期，64×64的变换块的延迟为145个时钟周期.本研究所提转置存储器基于双口SRAM实现，使用对角线存储方式并设计统一的数据映射方案，采用读写指针的方式并配合存储块信息的FIFO来实现转置存储.相比于乒乓存储的结构，本研究的方案能够结合VVC高频置零的特性减少一半的存储空间.本研究所提结构可以满足VVC硬件编码高性能的需求，比传统方案的面积和功耗更小.由于VVC变换核与变换尺寸的增加，计算逻辑需要的资源也大幅度增加，若想追求更小的面积，可以考虑使用通用乘法器的结构并降低并行度满足轻量化的需求.