内燃机排气凸轮-滚轮副异常工况下热弹流润滑分析*

晁 珅 朱桂香 王 娜 李书义 郭 峰 李常腾

(1.内燃机可靠性国家重点实验室 山东潍坊 261061；2.潍柴动力股份有限公司 山东潍坊 261061；3.青岛理工大学机械与汽车工程学院 山东青岛 266520)

凸轮-挺柱接触作为内燃机配气机构的重要摩擦副，由于持续承受高温、高速、时变接触曲率半径、交变压力等苛刻工况，接触表面容易产生严重的磨损，影响配气机构的工作精度进而降低发动机性能。而油润滑可以有效地减小两者间的磨损，降低运行过程中摩擦功率损失，在凸轮-挺柱接触中起着重要的作用。凸轮-挺柱的接触一般分为凸轮-平底(或菌式)接触和凸轮-滚轮接触。凸轮-平底(或菌式)接触的工作条件最为苛刻，其弹流润滑计算极具挑战性，已有的研究多针对此进行。如HOLLAND[1]在早期内燃机凸轮润滑分析中，简单地将润滑的卷吸效应和挤压效应进行叠加；DOWSON等[2]使用准稳态方法，探讨凸轮接触副的弹流润滑。随后，随着数值计算方法或实验技术的进步，人们分析了凸轮润滑中的热效应[3]、瞬态效应[4]、混合润滑[5]、表面粗糙度[6]、切向振动[7]等因素的影响，对凸轮-平底挺柱的润滑问题的认识也逐渐完善。

凸轮-滚轮挺柱(如图1所示)将凸轮-平底挺柱的滑动摩擦变为滚动摩擦，减小了摩擦力及磨损，已应用到越来越多的内燃机机型中。与凸轮-平底接触相同，凸轮-滚轮挺柱接触同样存在润滑状态的剧烈变化，且会发生滚轮与凸轮间的打滑、位置偏斜等，对润滑造成不利影响。DUFFY[8]、 LEE 等[9]早期使用模拟试验证明了凸轮与滚子间相对滑动的存在。近年来，KHURRAM等[10-11]通过实验分析了导致凸轮-滚子副打滑的主要因素。在凸轮-滚轮接触副的润滑理论方面，早期LEE等[9]、 CHIU[12]、JI 和TAYLOR[13]都建立了简化的凸轮-滚子润滑模型，对凸轮-滚子接触的滑动进行理论估计，表明最大的摩擦和滑动可能发生在凸轮鼻尖两侧或负载较低的基圆区。SHIRZADEGAN等[14]建立了等温的时变有限长接触弹流模型，求解了凸轮-滚轮接触的油膜建立的动态效应，同时以滚轮-平面的稳态接触研究了滚轮的凸度效应。近期ALAKHRAMSING等[15]在有限线接触中进行了凸轮-滚轮单元等温时变EHL全数值解，表明在高负载条件下滑动很小。同时ALAKHRAMSING等[16]研究还发现，滚轮-销轴摩擦力较大时，凸轮-滚轮发生明显的滑动，但其模型中没有考虑瞬态效应。朱建荣等[17]通过时变热弹流的完全数值解分析了进气滚轮凸度对凸轮-滚轮润滑的影响。

图1 内燃机凸轮-滚轮机构Fig.1 Cam-roller pair in internal combustion engine

综上所述，目前已有的研究侧重点不同，考虑的因素也不相同。因此，通过凸轮-滚轮润滑的完全数值解，分析多因素的共同影响是目前理论分析的重要方向。

本文作者对某型号内燃机排气凸轮-滚轮副润滑特性进行了研究，建立了有限长线接触条件下瞬态热弹流润滑数学模型及数值求解方法，研究了实际载荷工况下打滑、偏斜及热效应共同作用下凸轮-滚轮接触副润滑状态变化规律，表明有必要把凸轮与滚轮间偏斜现象纳入凸轮-滚轮摩擦副初期设计，并以凸度设计进行。文中结果可为凸轮-滚轮副润滑设计提供一定的数据依据。

1 理论模型

1.1 基本方程

针对于凸轮与滚轮接触副，采用时变工况下广义Reynolds方程[18]：

(1)

式中各当量符号定义如下：

式中：p为油膜压力(Pa)；h为膜厚(m)；ρ为润滑油的密度 (kg/m3)；η为润滑油黏度(Pa·s)；ua和ub为凸轮和滚轮固体表面速度(m/s)。

凸轮-滚轮副为有限长线接触副[19]，滚轮表面进行一定凸度修形，其膜厚方程：

(y≤ 0时，取+；y>0时，取-)

(2)

式中：fΔ是一个符号函数，当|y|>l/2时，fΔ= 1，当|y|≤l/2时，fΔ=0；h0(t)为刚体中心膜厚(m)；E′为综合弹性模量(Pa)；htd和Rd分别为滚轮凸度及端部倒角(m)；Rx为凸轮与滚轮的综合曲线半径(m)；s(y)为凸轮-滚轮相对偏斜项，其表达式为

s(y)=ytanφ

式中：φ为偏斜角度。

黏度方程：

η=η0exp{A1×[-1+(1+A2p)z0(A3/A4)-s0]}

(3)

式中：A1=lnη0+9.67；A2=5.1×10-9Pa-1；A3=1/(T0-138)；A4=138/(T0-138)；Z0=α/(A1A2)；S0=β0/(A1A3)；α为黏压系数(Pa-1)；β0为黏温系数(K-1)；Z0和S0为常数；T为润滑油温度(K)；T0为环境温度(K)。

密度方程：

ρ=ρ0[1+C1p/(1+C2p)-C3(T-T0)]

(4)

式中：C1=0.6×10-9Pa-1；C2=1.7×10-9Pa-1；C3=0.000 65 K-1；ρ0为润滑油的环境密度(kg/m3)。

载荷方程：

∬pdxdy=w

(5)

式中：w为接触副实时载荷。

不考虑体积力和热辐射的影响，并忽略沿x和y方向的热传导，将黏性流体流动的能量方程与连续性方程联立，可得到润滑油膜的能量方程[20]：

(6)

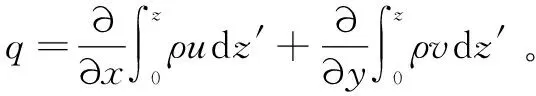
式中：c为润滑油比热容(J/kg·K)；u、v分别为润滑油沿x、y方向的流速(m/s)；k为润滑油的热传导系数(W/(m·K))。

固体a、b的热传导方程：

(7)

式中：ca、cb为固体a、b的比热容(J/(kg·K))；ρa、ρb为固体a、b的密度(kg/m3)；ua、ub为两接触固体表面沿x方向的速度(m/s)；ka、kb为固体a、b的热传导系数(W/(m·K))。

摩擦因数的计算公式为

(8)

1.2 边界条件

(1)Reynolds方程的边界条件

p(xin，y)=p(xout，y)=p(x，yin)=p(x，yout)

p(x，y)≥0(xin≤x≤xout，yin≤y≤yout)

(2)在油膜入口处非逆流区，油膜能量方程的边界条件

T(xin，y，z)=T0

而在入口处逆流区及计算域的其他3个出口边界上均不需要边界条件。

(3)固体a热传导方程的边界条件

T(xin，y，za)=T0，T(x，y，-d)=T0

(4)固体b热传导方程的边界条件

T(xin，y，zb)=T0，T(x，y，d)=T0

(5)将油膜能量方程与固体热传导方程联立求解时，油膜与固体界面上应满足热流连续条件

1.3 数值求解方法

建立凸轮-滚轮型有限长线接触热弹流模型，对以上各方程进行量纲一化，然后采用多重网格法、多重网格积分法[21]和逐列扫描法[22]求解接触副压力、膜厚和温度。其中最高层上网格节点数为129×769，取x、y方向边界计算域为

{(x，y)|-3.0b≤x≤2.5b，-0.5L≤y≤0.5L}

此外，在z轴方向上，求解域边界坐标为za=-d，zb=d，d=3.15b。d为固体a、b的温度渗透层厚度(m)。此外，收敛精度为载荷和压力的相对误差均小于等于1×10-4，温度的相对误差小于1×10-5。

2 结果与讨论

文中以凸轮-滚轮型摩擦副为研究对象，分析凸轮周期旋转过程中接触副润滑问题。计算工况凸轮转速ω=950 r/min，而两固体及润滑油所采用的公共输入参数见表1。

表1 固体和润滑油参数Table 1 Parameters of solid and lubricating oil

根据实际工况内燃机凸轮的升程、转速和滚轮半径等已知参数进行运动学分析，如图2所示，可以得到计算模型所需的运动副接触点的凸轮表面速度ua和综合曲率半径Rx，而实时载荷w则是由实际测量所得。若凸轮与滚轮两者做纯滚运动，则滚轮表面速度ub=ua。再结合实际测得的排气凸轮副载荷谱，就可进行完整周期内排气凸轮-滚轮副的润滑分析。

图2 一个完整周期内凸轮-滚轮副升程、载荷、综合曲率半径和凸轮表面速度变化Fig.2 Cam lift，load spectrum，reduced radius and entrainment velocity of the cam-roller contact in a cam rotation cycle

图3所示为一个周期内凸轮-滚轮接触副膜厚、压力、温升和摩擦因数的变化，其中滚轮凸度htd= 4 μm、偏斜角φ=0°和打滑系数kSRR=0。可以看出，整个凸轮旋转周期内各参数曲线的变化可分为平稳期和波动期，且各参数值发生变化的大体规律相似，其中在0°～52°和202°～360°范围内接触区润滑状态稳定 (即平稳期)，处于凸轮半径的平滑区，而中间52°～202°阶段润滑参数变化剧烈(即波动期)，对应配气机构气门排气开启和凸轮升程的改变，故润滑参数的改变与实际工况条件(凸轮升程)的改变规律相对应；在凸轮转角62°时，摩擦副会呈现出整个周期内膜厚最低和压力最高的润滑状态，由于此时正处于气门排气开启时刻，接触载荷突变至约7 000 N。与此同时，在波动期内中心膜厚和最小膜厚、中心压力和最大压力的波动幅度均较大，最大波幅可达到0.277 μm和0.892 GPa。而中心膜厚始终远高于最小膜厚，两者差值最大可达到0.533 μm，最大压力同样也始终大于中心压力，两者差值可达0.556 GPa。此外，在波动期内摩擦副温升和摩擦因数也发生了一定改变，但相对变化幅值均十分微小。因此，在纯滚条件下，凸轮-滚轮副润滑分析中可以忽略摩擦副温升和摩擦力。

图3 一个周期内膜厚、压力、温度和摩擦因数的变化规律Fig.3 Film thickness，pressure，temperature and frication coefficient in a cam rotation cycle

2.1 打滑问题

理论上，内燃机配气机构中主动凸轮带动从动滚轮做纯滚运动，但由于构件运动惯性或者滚轮与销轴间摩擦力的存在，滚轮接触表面可能不会对凸轮表面速度的变化立即产生反应，而存在一定的延迟，从而使两固体表面产生打滑现象；或者苛刻工况(如接触副曲率、载荷等参数突变)也可能会造成凸轮与滚轮间产生间断性的相对滑动。因此，十分有必要分析凸轮与滚轮间打滑对接触区润滑状态带来的影响。

假设凸轮与滚轮之间的相对打滑模型如图4所示，其中kSRR为打滑系数(kSRR=1-ua/ub)。已有研究指出，在低负荷区域(通常在凸轮基圈内)，滚轮最容易发生打滑[10-13]，负荷的增加会减少打滑的发生。因此，根据实际的载荷，定义在低荷载区(Ⅰ)打滑系数为常数值，在重荷载区(III)为0，而在中荷载区(II)打滑系数线性变化，连接其他2个区域的打滑系数。

图4 打滑情况下凸轮与滚轮表面速度示意Fig.4 Surface velocity schematic of cam and roller under the relative sliding conditions

图5给出了3个打滑系数下中心膜厚、中心压力、最大温升和摩擦因数的变化曲线，其中滚轮偏斜角φ=0°。可以看出，凸轮与滚轮间发生打滑时接触区内中心膜厚有微小的改变，而中心压力却几乎未发生变化，故可以忽略打滑对接触区膜厚和压力的影响。值得注意的是，接触区最大温升和摩擦因数对运动副打滑现象却十分敏感，这是由于2个固体表面之间的相对打滑会导致润滑膜的黏性剪切增强。在重载区Ⅲ，由于凸轮与滚轮间不存在打滑，该阶段接触区几乎没有温升和摩擦；而在过渡区Ⅱ(100°～156°)出现了较大的温升和摩擦力，这归因于相对较大的载荷及较高的卷吸速度共同作用。可见，在较高负荷的情况下，一旦发生打滑现象，将会给运动副带来不利影响，对接触副润滑性能有着显著影响，主要表现在接触区温升和摩擦因数的变化。

图5 一个周期内凸轮滚轮打滑对膜厚、压力、温度及摩擦因数的影响Fig.5 Effect of sliding on film thickness，pressure，maximum temperature rise and friction coefficient in acam rotation cycle

为了深入分析凸轮与滚轮间打滑影响的规律性，图6给出了3个凸轮转角(θ=0°、127°、182°)处最大温升和摩擦因数随打滑系数的变化曲线，其中滚轮偏斜角φ=0°。可以看出，随着打滑系数的增加(即两表面滑滚比增加)，接触区油膜最大温升却持续上升，但上升趋势会逐渐减缓，由于两运动表面间打滑越严重，油膜剪切率会越大，热耗散必然越大，最大温升也就越大，其又会降低接触区润滑油黏度，进而导致接触区油膜的降低；而摩擦因数则呈现出先上升到极值后下降的变化，且后期下降趋势也会逐渐减缓，这是由于在打滑程度增加过程中剪切率的增加和黏度降低的综合作用结果。可见，凸轮与滚轮间打滑必然会弱化接触区润滑状态。

图6 凸轮滚轮不同打滑程度对接触区油膜温度和摩擦因数的影响Fig.6 Effect of the cam-roller sliding on the temperature rise and friction coefficient

为了尽可能地降低凸轮与滚轮间打滑产生的不利影响，文中从润滑油黏温系数方面进行了探讨。 凸轮和滚轮存在一定滑动条件(kSRR=0.1)下，3个凸轮转角(θ=0°、127°、182°)处中心膜厚、油膜最大温升和摩擦因数随润滑油黏温系数的变化曲线，如图7所示。可以看出，随着黏温系数的增加，润滑油黏度降低，接触区中心膜厚、油膜温升和摩擦因数均会逐渐减小，相对来说中心膜厚下降幅度不大，但油膜温升和摩擦因数却下降趋势十分明显，故在保证接触区能实现有效润滑条件下可以尽可能选择较大的黏温系数，可有效地降低表面相对滑动造成的不利影响。因此，黏温系数可以通过润滑油的黏度影响接触区润滑状态。

图7 滑动条件(kSRR=0.1)下润滑油黏温系数对中心膜厚、接触区温升和摩擦因数的影响Fig.7 Effect of viscosity-temperature coefficient of lubricating oil on the center film thickness，temperature rise and friction coefficient under the certain sliding condition (kSRR=0.1)

2.2 滚轮偏斜问题

凸轮-滚轮副是一种典型的有限长线接触副，该类运动副最大特点就是接触区狭长，造成在实际工况中很容易发生接触副偏斜(凸轮轴线与滚轮轴线产生一定夹角φ)，故非常有必要分析一定偏斜工况下排气凸轮-滚轮副的润滑情况及针对该类工况的优化。

图8给出了3种不同偏斜角度下凸轮-滚轮副接触区x= 0截面膜厚和压力曲线，其中滚轮凸度htd=4 μm，打滑系数kSRR=0。可见，凸轮与滚轮在理想接触情况(即正常接触φ=0°)下膜厚和压力沿着轴线方向对称分布，但当凸轮与滚轮轴线不再平行(即非正常接触φ≠0°)时，接触副呈现出偏斜现象，接触区膜厚和压力分布将不再对称分布，而是在接触副的一端产生压力集中且膜厚降低，接触区润滑状态恶化。图9所示为3个不同凸轮旋转角度下接触区最小膜厚和最大压力随偏斜角的变化曲线，可见凸轮与滚轮的偏斜会造成最小膜厚的减小和最大压力的增大，偏斜角越大润滑状态恶化越严重。一旦凸轮-滚轮副出现偏斜，将会明显降低最小膜厚和增大最大压力，其后果就是增加了润滑油膜破裂的可能性和压力分布的不均匀性。因此，凸轮-滚轮副中偏斜现象会恶化接触区润滑，增加润滑失效的可能性。

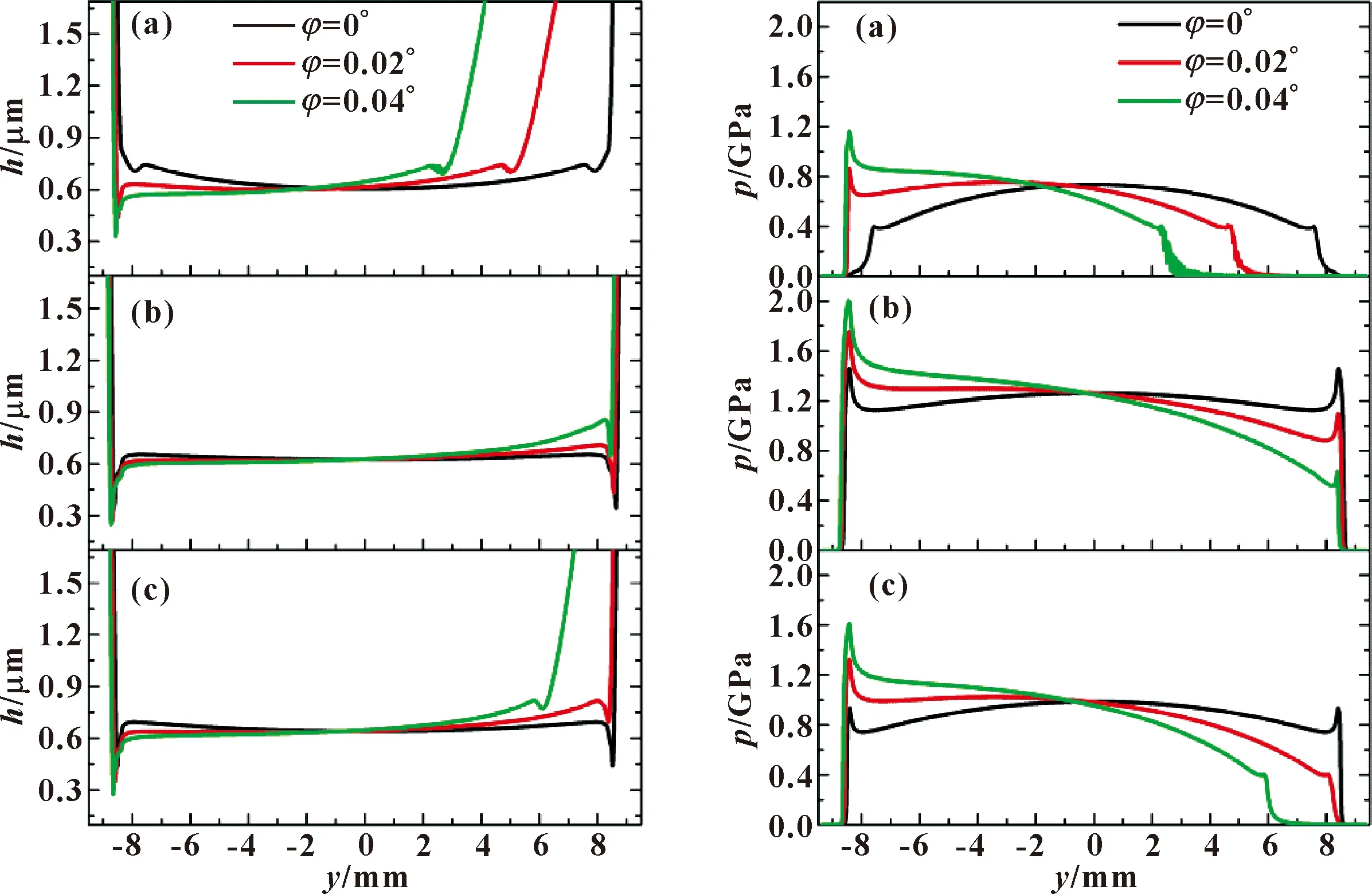
图8 不同偏斜角下3个凸轮角位置x=0截面接触区膜厚和压力分布：(a)θ=0°；(b)θ=62°；(c)θ=182°Fig.8 Film thickness and pressure profiles at x=0 for three tilting angles at three cam angles：(a)θ=0°；(b)θ=62°；(c)θ=182°

图9 偏斜角度对接触区最小膜厚和最大压力的影响Fig.9 Effect of tilting angles on the maximum pressure and minimum film thickness

为了降低凸轮-滚轮副偏斜现象导致的不利影响，在前期摩擦副设计时就需采取一定的优化手段，最直接的方法就是对滚轮进行凸度修形。假设接触副存在一定偏斜角度(φ=0.04°)，图10给出了3个关键凸轮转角(θ=0°/62°/182°)处滚轮凸度对接触区最大压力和最小膜厚的影响，其中打滑系数kSRR=0。

图10 0.04°偏斜角度下滚轮凸度对接触区膜厚和压力的影响Fig.10 Effect of roller convexity on maximum pressure and minimum film thickness under tilting angle of 0.04°

由图10可以看出，随着滚轮凸度修形的增加，最小膜厚明显升高，最大压力明显降低，在一定程度上改善了接触副偏斜现象带来的润滑不利影响。但滚轮凸度修形的改善效果并不是一直有效的，不同条件下存在着最佳值，如凸轮转角0°、62°、182°处对应着不同的最佳滚轮凸度值，若以膜厚为参考最佳滚轮凸度值分别约为9、15和13 μm，超过此最佳值后最小膜厚基本维持不变，而计算得到的中心膜厚继续降低；若以压力为参考最佳滚轮凸度值分别约为8、12和11 μm，超过最佳值后中心压力和最大压力均有微弱升高。根据优先考虑降低润滑油膜破裂可能性再尽量实现接触区压力均匀分布的原则，该工况下最佳的滚轮凸度修形约为15 μm。因此，非常有必要把凸轮与滚轮间偏斜现象纳入凸轮-滚轮摩擦副初期设计，且选择合适滚轮修形以改善其不利影响。

3 结论

通过数值计算模拟了实际排气载荷图谱下凸轮-滚轮副一个周期内的润滑状态，分析了运动副打滑和偏斜对润滑性能的影响，并探讨了接触区润滑改善方法，得到如下结论：

(1)一个周期内凸轮-滚轮副润滑状态可以分为平稳期和波动期，与排气工况变化相对应，且纯滚条件下可以忽略摩擦副的温升和摩擦力。

(2)凸轮与滚轮间的打滑现象最突出的影响就是接触区温升和摩擦因数，降低了接触区润滑性能，而合适的黏温系数则会改善接触区润滑。

(3)凸轮-滚轮副中偏斜现象会恶化接触区润滑，增加润滑失效的可能性，若采用恰当的滚轮凸度可以在一定程度上缓解其造成的不利影响。