脉动热管计算流体力学模型与研究进展

卜治丞，焦波，林海花，孙洪源

（山东交通学院船舶与港口工程学院，山东 威海 264200）

脉动热管（pulsating heat pipe, PHP）又称振荡热管（oscillating heat pipe, OHP），是1990年由日本学者Akachi[1]提出的一种热管结构。它主要有管式和板式两种形式，如图1所示，前者是由封闭的毛细管弯曲成蛇形结构，适合包裹几何形状复杂的热源；后者是在平板上加工闭合通道，能与扁平热源保持良好的热接触，并且易于微型化。PHP与传统热管相比，无需吸液芯来完成工质循环，具有体积小、结构简单、成本低、适应性强、传热性能极佳等优点[2]，在诸多热传输领域都具有极高的应用潜力。

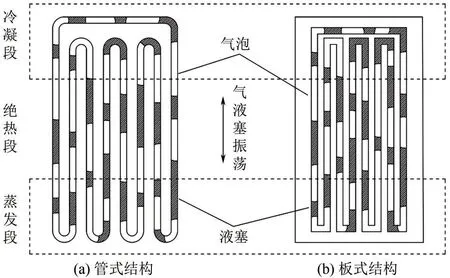
图1 脉动热管两种基本结构

PHP内的工质是多种因素控制的气液两相流系统，虽然结构简单，但运行机理较为复杂、影响因素较多[3]。目前普遍使用Bo数来判断PHP能否正常运行，如式(1)所示，它用来计算PHP内径的取值范围，通常认为Bo数合理的区间在0.7～2 之间[4]。此外，弯折数N、充液率FR、倾角θ、重力环境、壁面润湿性、几何结构、工质物性、加热功率Q（或热流密度q），这些参数之间相互影响共同作用于管内，影响工质的流动状态与振荡特性。

由于PHP 内独特的往复振荡运动与工质流型变化，基于准平衡过程的经典热力学不能完全分析其传热与流动机理[5]。众多学者从实验、理论和模拟上对PHP 的机理开展了大量的研究工作，已有的可视化研究在不同工况下观察到的流型主要包括四种：泡状流、塞状流、半环状流和环状流。另外，随着计算机性能的大幅提升与数值计算技术的进步，通过理论模型预测PHP 运行状态、辅助可视化实验量化分析管内的振荡与传热特性、指导PHP 的优化设计，成为PHP 研究的热点问题。迄今为止，已有经验关联式、人工神经网络、一维数值模拟和计算流体力学（computational fluid dynamics,CFD）模拟等较为准确地分析和预测PHP流动与传热的方法[6]。其中，经验关联式通常都具有一定的适用范围，预测该范围以外的工况具有高度的不确定性；人工神经网络通过有效的训练可以成为稳态条件的强大设计工具，但它不能分析所涉及的物理现象。相比之下，一维数值模拟与CFD 模拟都遵循“质量-动量-能量”守恒建立的偏微分方程求解瞬态参数，结果更具物理意义。

2001 年Shafii 等[7]首次公开发表了一维数值模拟的研究成果，简化弯折处产生的压降，将PHP近似成一根直管以满足单一维度对模型的限制，只考虑了塞状流，假定液膜厚度均匀并需要将其预先确定并作为拟合参数。经过多年发展，已有文献提出能够允许液膜厚度和长度发生改变的模型，模拟的准确性大幅提升[8-9]，有学者认为它是表征物理现象和所需仿真时间之间的最佳选择[10]。2009 年Liu 等[11]首次公开发表了利用CFD 模拟PHP 的研究成果。尽管需要的时间与计算资源巨大，但近年来CFD 模拟仍然受到了许多学者的关注，这主要是由于它可以得到诸多一维数值模拟尚不能分析的问题，同时可以促进一维数值模拟的进一步发展。

目前已有相关综述[12-14]以强化换热、纳米工质和板式结构等为侧重点对PHP 的研究成果进行详细汇总。根据公开发表的文献，尚未有研究对CFD模拟PHP 涉及的各种模型、求解方法及存在的问题进行梳理与总结。本文将对比和分析CFD 模拟PHP 的相关文献（具体信息详见表1），首先介绍CFD 模拟对PHP 特征现象描述的优势，然后对上述问题进行讨论，提出现有模拟研究存在的问题及未来发展的方向。

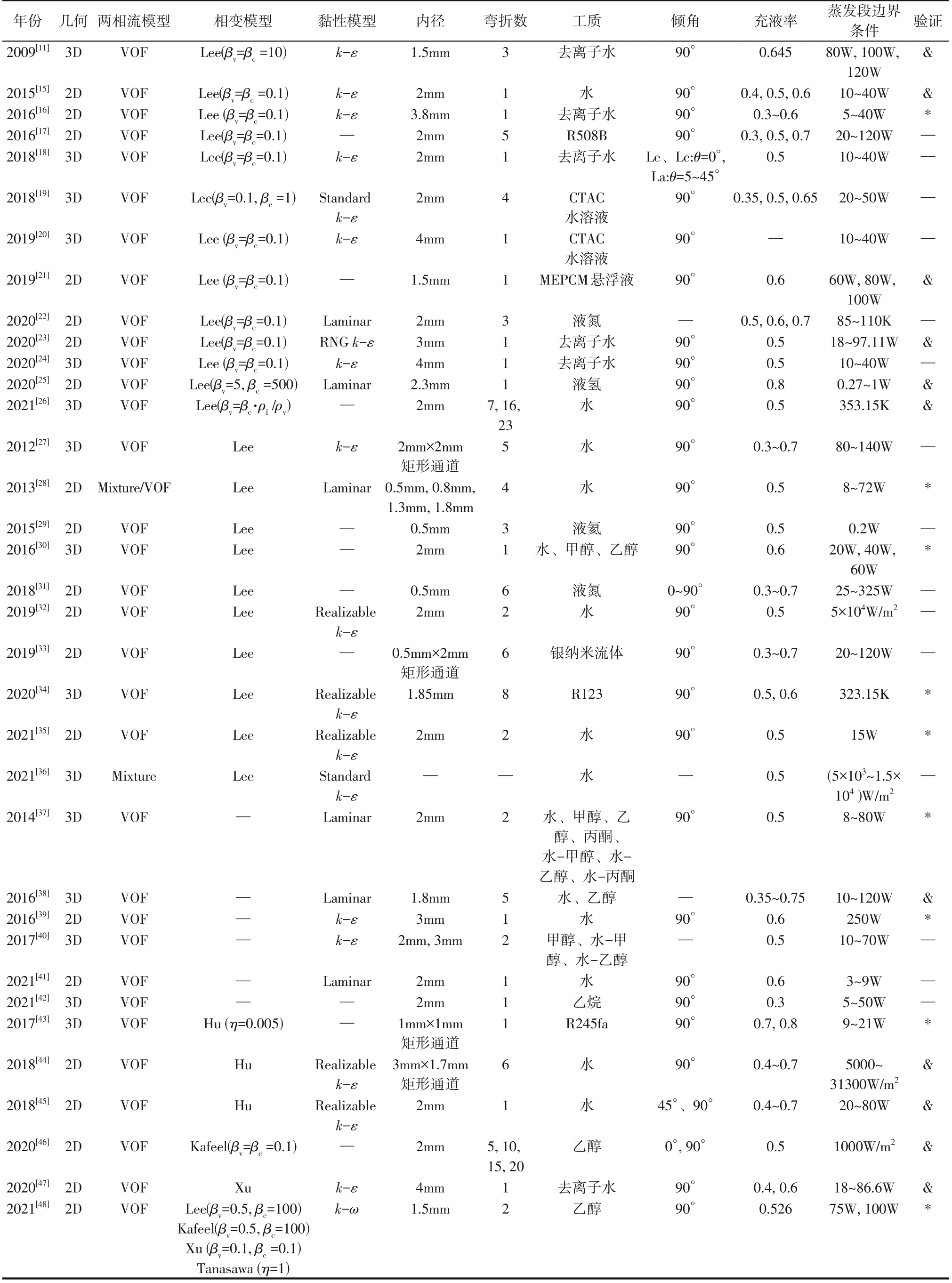
表1 CFD模拟文献总结

1 PHP特征

PHP管径较小，工质在表面张力的作用下形成间隔布置的气液塞。在蒸发段，气塞与管壁之间的液膜不断蒸发，气泡膨胀，推动气液塞流向冷凝段，同时冷凝段气泡凝结收缩；在工质蒸发和冷凝的共同作用下产生往复振荡运动的压差，实现高效传热。运行中的PHP 内部工质温度和压力瞬时变化，流动变得无序和杂乱，因此PHP 内气液相的传热传质具有显著的特殊性，这些现象在传统热管中可以忽略。

虽然PHP 内工质主要的流型为塞状流，但在相变作用下会出现频繁的流型转换，气液相界面的形态也随之改变，CFD模拟可以体现从泡状流到环状流之间所有流型转换。另一个主要特征是工质振荡时的压降，由于弯液面的影响，液塞前后弯液面附近的压降不能直接应用单相流的压降公式，需要添加修正项[49]，特别是PHP本质上是温度驱动的自激振荡过程，流动速度不可控制。CFD模拟的矢量具有实际的方向，能够获得工质振荡过程中的压力损失，尤其是在弯折处的压降，这些信息可以促进一维数值模拟的发展。

气泡的状态会决定相变发生的条件。根据Noh和Kim 等[50-51]的研究工作可知，PHP 中的气泡主要是过热的，这意味着可以用饱和温度来判断相变是否发生，饱和压力的影响可以忽略，这为模拟中定义相变发生的条件提供了便利。

液膜是影响热管传热传质的关键部分。基于薄膜相变传热的实验证明，通过薄液膜的潜热交换比液塞运动引起的对流换热更强[52]。在PHP内的液膜不同于其他毛细热管纳米级的润湿液膜，它是在黏性力和毛细力共同作用下由弯液面沉积形成的微米级沉积液膜[53]。弯液面曲率的变化对沉积液膜厚度有决定性影响，沉积液膜的厚度会很大程度影响传热，CFD模拟可以很好地揭示液体惯性对弯液面曲率的影响。然而，在液膜细节的表现上，比如液膜破裂处形成如图2(a)所示的脱湿脊（dewetting ridge）[54]、振荡时弯液面与液膜线的交界处会出现图2(b)所示的随时间变化的波形[55]，暂时还没有CFD模拟实现。

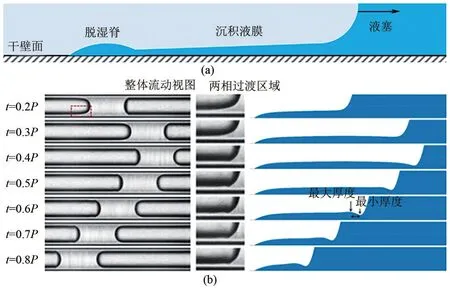
图2 蒸发段液膜组成[54](a)和振荡中的毛细冲击[55](b)

2 CFD模型

CFD 模拟基于有限体积法将气液两相流模型、表面张力模型、相变模型和黏性模型与守恒方程结合。文献中两相流模型多使用流体体积（volume of fluid, VOF）法，表面张力通常使用连续表面张力（continuum surface force, CSF）模型，相变模型以Lee模型为主。本节将总结不同研究中对模型的选取和细节设置，介绍PHP 模拟中计算的逻辑，并指出仍需完善之处。

2.1 气液两相流模型

PHP气液两相流复杂流型的求解适合采用将每相当作连续相的欧拉-欧拉法。以欧拉-欧拉法为基础拓展有多种两相流模型，气液两相流的计算中常用到Mixture模型和VOF模型。Lin等[28]对两种模型进行对比分析，发现Mixture 模型预测PHP 的温度值相较于VOF 模型具有更高的准确性。Mixture模型允许两相相互掺混，对于捕捉气液相界面并不敏感，不适用于流型的研究，应用于少数只侧重于温度精度要求、对流型要求相对低的研究中；而VOF模型自Hirt和Nichols[56]建立以来就凭借能够更加灵活有效地处理复杂的自由边界问题著称，既能保证物理量准确又能兼顾流型特征，成为PHP 模拟预测研究的普遍选择。气液界面位于0<αv<1 的位置。在每个控制体积中，所有相的体积分数总和为1，见式(2)。对各相之间的界面的跟踪是通过求解该相体积分数的连续性方程来完成的。

液相与气相的连续性方程分别如式(3)和式(4)所示。

液相与气相的动量和能量守恒共用一套方程，如式(5)和式(6)所示。

在守恒方程中最关键的问题是表面张力引起的动量源项Ss和相变产生的质量源项Sm，它们需要通过2.2节与2.3节所涉及的模型解决，能量源项Sh通过式(7)获得。

VOF 通过Geo-Reconstruct 几何重构用分段逼近的方法表示流体间的界面，每个单元内具有一个线性斜率，得到气液混合单元内近似真实的相界面形状。混合单元内的热导率λ、密度ρ、黏度µ通过体积平均确定，能量E由质量平均获得。虽然VOF模型相比于其他两相流模型优化了界面的捕捉，但液膜处相界面的曲率相对平滑，要得到液膜的具体形状需要在壁面附近对网格作微米级的加密，以提供足够的网格去重建相界面。但是加密网格势必带来库朗数（Courant number）的增大，需要更小的时间步长来控制流体时间步长和空间步长的相对关系，这对时间步长本就在10-4～10-5s 的模拟来说，更加大了模拟所需的计算时间和资源。

2.2 表面张力模型

表面张力影响PHP内气泡的生长、流动。常见的模拟表面张力的模型有两种：CSF模型和连续表面应力（continuum surface stress, CSS）模型。研究中通常使用CSF 模型，也有研究使用CSS 模型[26]。CSF模型和CSS模型都只需要确定其中一相体积分数即可[57]。CSF 模型将作用在液体界面上的表面力用散度定理转换为单元体内的体积力，作为添加到动量方程中的源项来模拟表面张力效应[58]，具体如式(8)所示。

由于VOF模型气液混合单元内的相界面为直线，因此不能保证相邻单元相界面连续，在表面张力主导的模拟中会产生虚拟流动（spurious currents）。普通直管内相界面是光滑的，虚拟流动对结果的影响很小。在管径突然发生变化或者有尖角的情况下，就需要考虑对虚拟流动进行修正[59]，目前对管径有变化的PHP 模拟中未有研究使用修正的表面张力模型。

2.3 相变模型

PHP内工质相变过程是影响流动与传热的重要因素，同时影响相界面连续性，模拟中需要用符合物理规律的相变模型计算蒸发和冷凝过程中气液相间质量传递，完成各相连续性方程和系统能量方程中源项的补充。由于离散网格的大小不全相同，CFD模拟中的相变模型通常需要调用网格单元内的体积变量或者密度变量，防止小体积单元内被加载上与体积大小不相符的源项。有关CFD模拟PHP文献中使用的相变模型都基于如式(10)所示的Hertz-Knudsen-Schrage 方程描述蒸发和冷凝过程。质量源项通过质量流量J与界面面积密度A的乘积获得，A是指发生相变的区域占整个单元的比例，表示该单元内相变发生的速率。表2给出了现有研究使用过的相变模型的关系和公式。

表2 CFD模拟PHP的相变模型

对于模拟过程主要为液体蒸发或气体冷凝时，Lee模型得到了广泛应用，它假设相变主要是由界面温度和温度偏差引起的，将相变经验系数η、无固定值的瞬态气泡直径db及多项物性参数变量的组合用蒸发、冷凝系数βe、βc来代替；保留气相（液相）的体积分数α和密度ρ是保证获得的相变量符合该单元的体积，如式(11)所示。在只发生蒸发或冷凝的相变模拟中，βe和βc通常以能够模拟相界面温度接近饱和温度为优[64]，但PHP内的工质在封闭系统中蒸发与冷凝，这涉及蒸发速率与冷凝速率之间的匹配，两者的选择尤为重要。从表1可以看出，在不同的模拟研究中，对蒸发系数βe取值范围从0.1 到10，冷凝系数βc从0.1 到500，取值范围较大且没有明确的调参标准，因此蒸发和冷凝系数的选取是Lee模型在PHP模拟尚未解决的问题。

有研究者提出用变系数的方法对Lee模型进行修正，假设任意时刻蒸发量与冷凝量保持一致，通过上一时间步长的蒸发量与冷凝量对比得出下一时间步长的系数。这个假设有两种实现形式：一种是Kafeel优化，如式(12)所示，保持βe不变，每时间步长修正βc；另一种是Xu 优化，利用式(12)与式(13)每个时间步长后同时修正两个系数。以上两个团队通过结果分析，都认为保证蒸发量与冷凝量的动态平衡能够改善PHP模拟中由Lee模型局限性造成的与实际不相符的传热恶化[46-47]。研究中发现，由于气体密度小于液体，Kafeel 优化会使βc迅速增大，导致计算发散；Xu 优化可以解决这种发散问题，但是βe降低后会出现蒸发量过少、蒸发段温度远超实际值的情况。

Tanasawa模型最初是针对冷凝问题推导出的，假设界面处温度跃变很小，即(T-Tsat)/T<<1，质量流量与相间温度跃变简化为线性关系。为了比较以上4 种模型描述流型的优劣，Błasiak 等[48]将如式(14)所示的Tanasawa 模型[61]与Lee 模型、Kafeel 优化、Xu 优化在相同工况下得到的模拟结果与可视化实验比较，认为Xu 模型得到的气塞形状更接近实验结果，如图3所示。

图3 实验中气塞结构(a)和相变模型模拟气液分布云图[48][(b)～(e)分别为Tanasawa模型、Lee模型、Kafeel模型、Xu模型。]

以上提到的模型都没有单独讨论对PHP 传热过程有重要影响的薄液膜的相变特征。Lee模型的相变量与单元内单相体积分数成正比，会导致薄液膜处蒸发换热能力较弱[65]。目前仅有胡伟男等[43]在2017年修订了相变速率的影响因素，认为对于亲水性好的工质，更容易出现薄液膜现象；而VOF 中贴壁网格气液混合单元的温度低于实际液膜处的温度，需要对薄液膜处的温度与相变源项进行修正，因此建立了如式(15)和式(16)所示的液膜相变模型。

2.4 建模方式

CFD模拟可以采用二维或三维模型（表1中3D和2D，即three-dimensional和two-dimensional），三维模拟可获取管内横剖面的参数信息（图4），还可以对非对称截面（如梯形、三角形等）PHP中的气液流动进行研究，但相较于二维模型网格数呈指数增加，计算资源要求较高。为节约计算资源，对于前后对称且不涉及空间上弯折的PHP，更多文献选用二维模拟。对于三维几何模型按照实际尺寸建模即可，而二维几何模型缺少深度尺寸，求解器认为本质上计算的是其沿平面法向向内延伸深度1m 后的三维模型[66]，由于二维模型单纯对平面几何体进行法向拉伸，因此弯液面与三维模型的形态上有所不同。

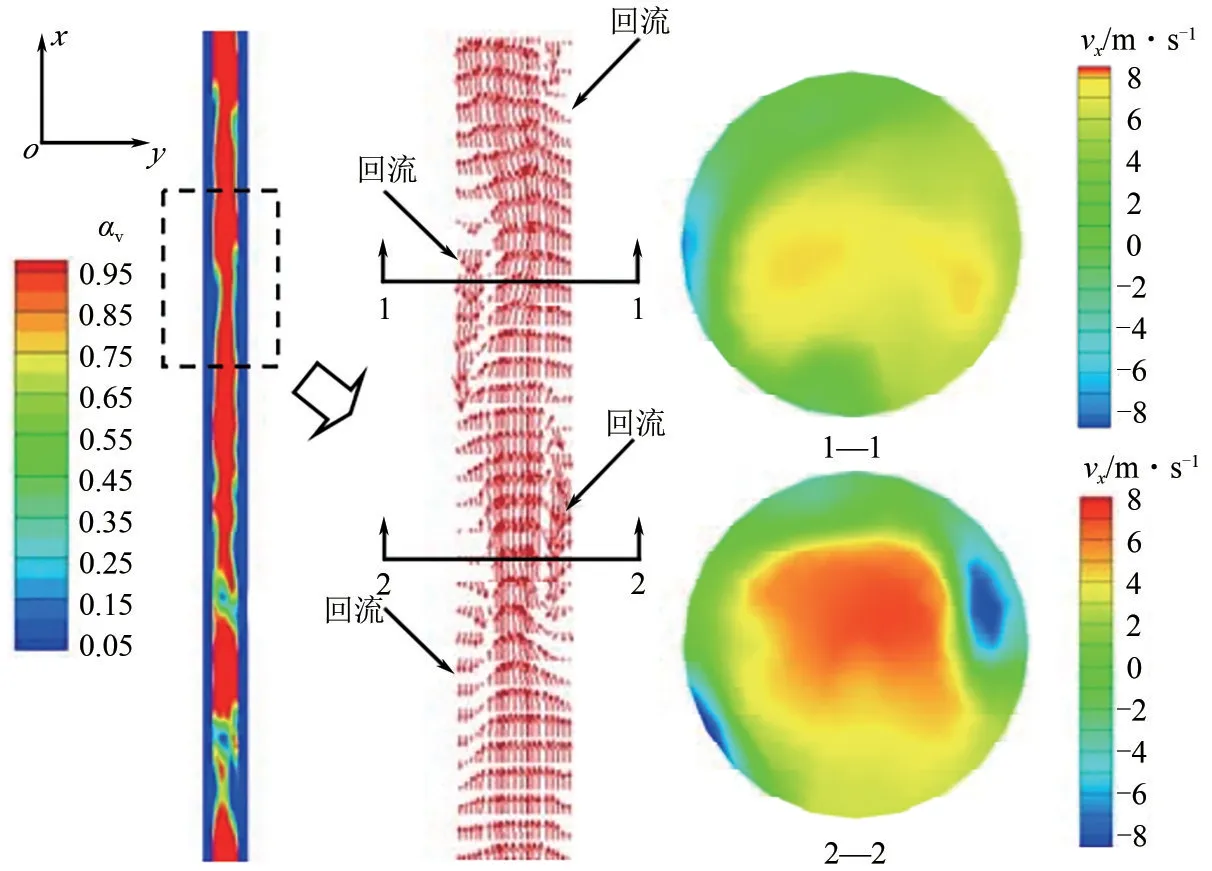
图4 三维模拟横剖面云图[11]

目前不同研究者对二维模拟中PHP 几何模型有两种处理方式：① 多数学者假定二维几何模型与实际差距微小可以忽略，直接用实际PHP 的管径建立二维几何模型进行计算与分析；② 也有学者提出根据Bo数可知[式(1)]，重力和表面张力在内径的选择上起重要作用，二维模拟中需要根据相似原理对液塞受到的重力G与表面张力Fs的分析来确定模型管径的取值[15,67]，表3 通过公式以圆管为例说明了分析的过程。在已发表的CFD 模拟中，研究者对上述两种方法得到结果的可靠性都在各自的研究中得到了验证，但目前尚缺少对两种二维模型管径选择的对比研究，其对模拟结果产生的影响仍未知。

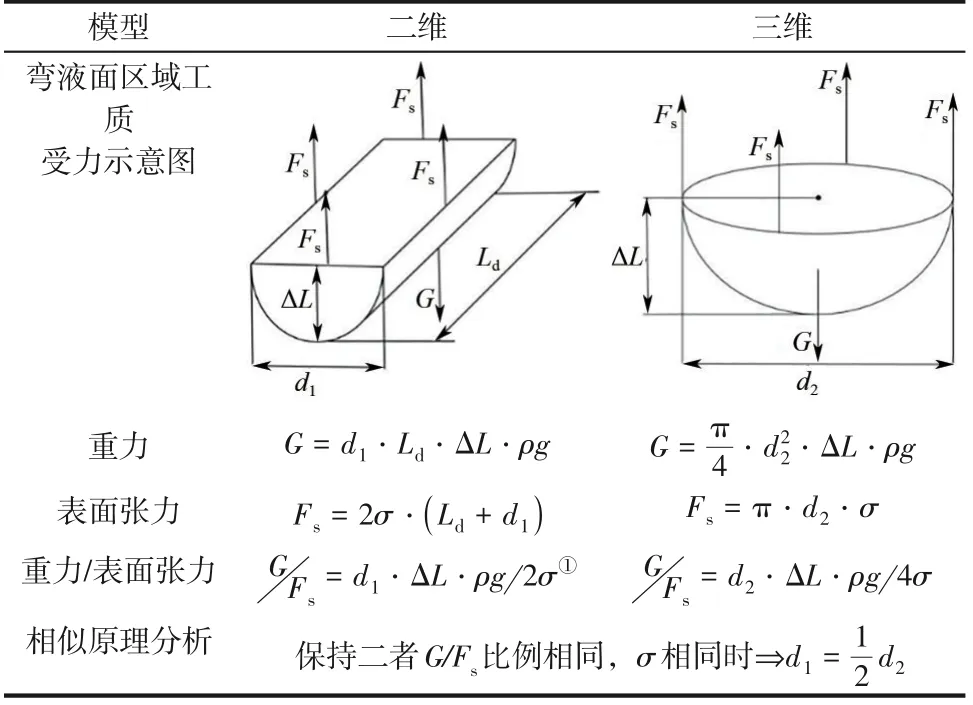
表3 直径在二维和三维模拟中的对比（以圆管为例）

3 CFD模拟研究进展

CFD模拟可以辅助分析实验条件难实现又至关重要的工况，如模拟低重力或超低温等极端环境下PHP的运行特征；还可以通过数值计算结果为通道结构提供改进方案。本节将总结通过CFD 模拟得到的主要参数对PHP性能的影响。

虽然目前我国有些事业单位正逐步加强对经费管控等方面的投入和研究，但是在具体操作过程中却将其“独立”，并未与财务管理机制紧密相连，使得经费管控与财务管理两者之间缺乏统一性和完整性。从核算形式的角度出发，经费管控是加强事业单位成本费用支出管理的一种有效手段。不仅如此，其还是事业单位向企业财务管理转变的一种过渡性的费用管理办法。因此，经费管控唯有与财务管理紧密贴合，相互补充与衔接，随财务管理的转型转变而获得提升。

3.1 重力加速度

放置方向（倾角θ）或者重力环境不同会改变管内工质沿管壁所受的重力加速度分量，它既可能促进PHP 的流动也可能抑制PHP 的正常运行。Sagar等[22]对底部加热N=3 的PHP（D=2mm，接近工质临界直径1.9mm）在不同重力环境（g=0.01m/s2、0.981m/s2、9.81m/s2）下进行模拟分析，结果说明临界直径附近微重力环境下表面张力起主导形成的流动更为稳定，并有更快的启动速度。图5给出了FR=0.5s、15s 时三种环境下PHP 的温度分布情况，可以看出微重力环境热量传递更均匀。Choi等[46]模拟θ=0°、N=5的PHP，发现蒸发段气泡无法抬升至冷凝段凝结，如图6(a)所示；而在倾角增大至重力加速度分量的影响大于表面张力时，气泡会形成图6(b)所示的不对称形状。上述模拟表明，在表面张力仍主导气泡形状且拥有较小重力加速度分量时可以增强流动的稳定性，但倾角θ为0 也会导致弯折数较少的PHP 管内无法形成振荡流动从而恶化传热。

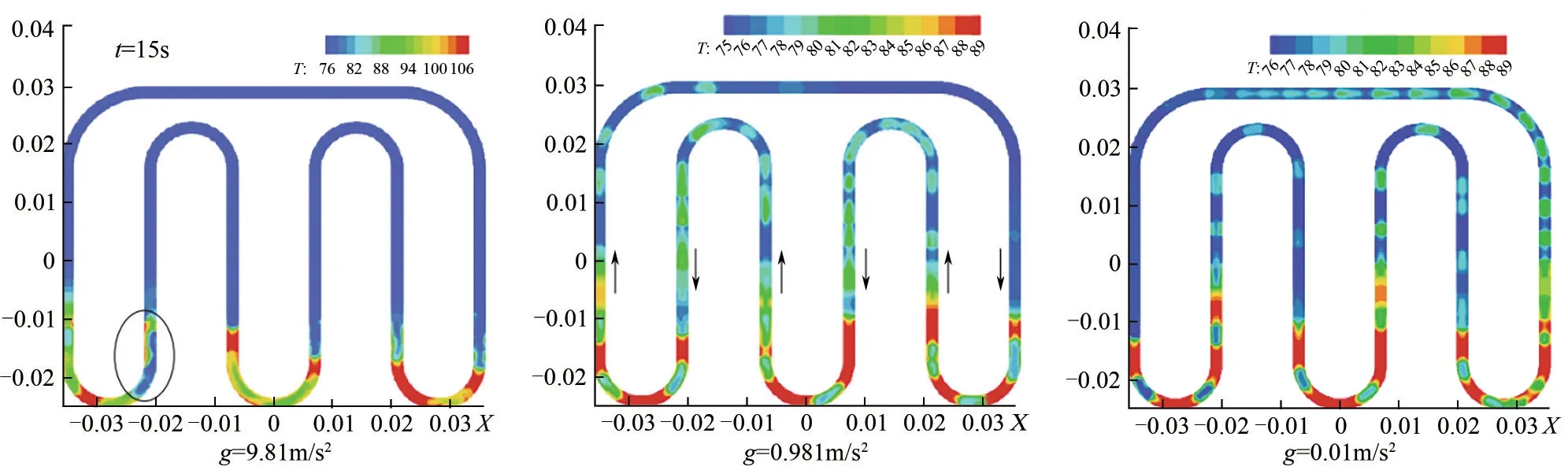
图5 不同重力环境PHP温度分布(FR=0.5s、15s)[22]

图6 水平放置(a)和重力加速度分量效应大于表面张力(b)时的运行状态[46]

3.2 弯折数

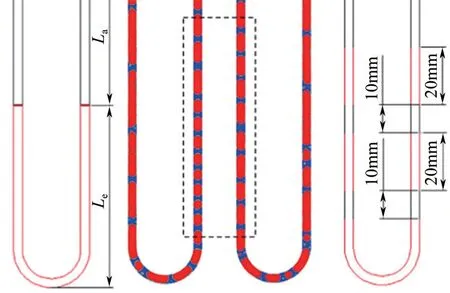
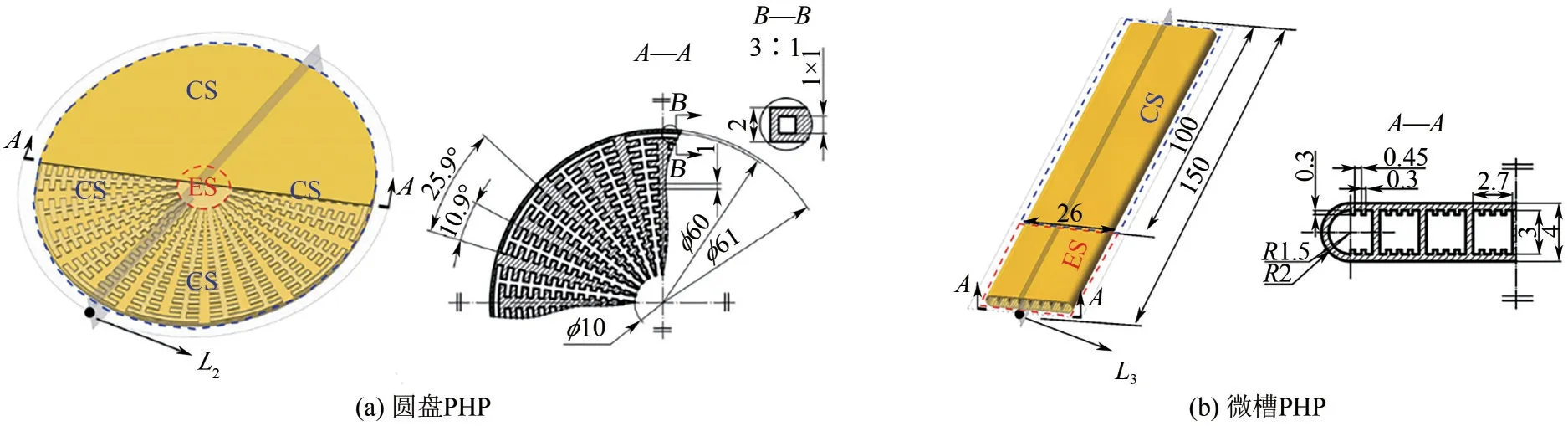
不同工况的PHP 都存在一个临界弯折数Ncrit，N≥Ncrit时装置性能受重力影响不大；而对于N

图7 蒸发段“烧干”(a)和正常运行(b)的气液分布云图对比[46]

3.3 蒸发和冷凝段

蒸发和冷凝段的尺寸影响气泡的生成和破灭，改变循环流动的能力。Wang 等[15]对PHP 不同蒸发冷凝段长度下的传热性能进行了比较，结果发现适当增大蒸发段或减小冷凝段的长度比值有利于加快启动，降低热阻；但在较低充液率（FR=0.3、0.4）和较大加热功率（Q=40W）共同作用下，冷凝段长度过小的PHP 会出现冷凝不彻底的气塞回流蒸发段而导致传热恶化的现象，热阻不降反增。Xie等[23]模拟了蒸发段间断不连续的PHP，与连续蒸发段相比发现前者很少出现流动方向改变和流动停滞的现象，流型始终保持在塞状流，没有出现泡状流（图8），并认为间断蒸发段能为工质提供类似泵的效果，对传热有很大帮助。

图8 蒸发段连续（左）和蒸发段不连续（右）PHP气液分布云图对比[23]

3.4 通道结构

有规律的管径变化可以改变通道结构，进一步优化PHP 传热性能。Xu 等[27]将板式PHP 的蒸发段流道分流，如图9(a)所示，低加热功率（80～110W）时，微槽引起的流场扰动会减弱传热能力；在高加热功率（110～140W）时，微槽引起的流场扰动会有效地增强传热，起到类似换热翅片的作用，得到了比流道不分流的PHP 更小的热阻。王迅等[44]比较截面渐变PHP的运行特性，如图9(b)所示，研究发现，随着大小截面比值的增加，中高热流密度（11000～31300W/m2）下PHP的启动优势明显提升，热阻先增大后减小；在大小截面比值为1.5∶1时传热能力达到最佳。鄂加强等[39]基于场协同原理分析，将PHP 左侧绝热段管径分别减少0.1mm 和0.3mm，如图9(c)所示，这种结构使PHP 具有更好的温度-速度协同效应，获得了更强的振荡频率，进而改善了传热性能。王迅等[45]对蒸发段管径增大的PHP进行了模拟，如图9(d)所示，结果发现启动时间变长，但稳定运行后脉动频率更大，温度振幅更小，有更好的均温性；大管径蒸发段还有助于向蒸发段液膜供液，增加蒸发段液膜的再湿润程度，提高传热极限。

图9 局部强化散热翅片PHP[27]、渐变式平板PHP[44]、局部窄管PHP[39]和变管径PHP[45]

Wang 等[16]分别对蒸发段、绝热段和冷凝段具有波纹结构的PHP 进行了模拟，如图10(a)所示，结果表明，蒸发段或冷凝段设置波纹结构降低了PHP的热阻，更有利于强化传热，绝热段波纹结构仅在较低充液率（FR<0.6）和加热功率（5～15W）下优于无波纹的PHP。蒋二辉等[32]在PHP上分别对每段布置具有锯齿结构，如图10(b)所示，研究发现其在冷凝段时装置具有最优的启动特性与传热能力。Wang 等[47]在PHP 冷凝段分别建立了膨胀、收缩管，如图10(c)所示，通过分析总结出膨胀管可诱导主流分离并中断热边界层，提高传热效率高达45%；而收缩管能够提供像泵一样的功能，从而提高振荡频率。

图10 波纹型PHP[16]、锯齿型PHP[32]和膨胀-收缩冷凝段PHP[47]

弯折处通道过渡是否圆滑也影响着PHP 的性能。Xie 等[23]模拟分析如图11(a)所示的直角弯折管与圆弯折管对PHP 运行状态的影响，研究发现，冷凝段的直角弯道对流型影响显著，有助于切断长气塞增加气液界面面积，使气体冷凝更充分。Zhang等[35]认为在绝热段相邻通道之间添加了连通管，如图11(b)所示，可以让一部分未凝结的气体再次经过冷凝段，减少回到蒸发段的气塞以预防烧干；模拟结果表明，倾斜度45°的连通管传热性能提升最大，60°连通管反而会使传热恶化。

图11 直角弯折管PHP[23]和连通管结构[35]

在应用领域模拟PHP 空间上变化的通道结构必须使用三维几何模型，对计算资源要求非常大，目前相关模拟较少。为了与散热设备配套生产应用，Wei等[36]设计了圆盘PHP模型和微槽PHP（图12），两种通道结构的PHP 在模拟中都可以正常运行，并观察到高热流密度（1.5×104W/m2）下微槽平板PHP蒸发段有瞬态高温出现，模拟结果为实际应用领域复杂空间下合理放置PHP提供了指导依据。

图12 圆盘PHP和微槽PHP(单位：mm)[36]

3.5 润湿性的影响

液滴在固体表面的润湿性通过接触角γ来描述，γ越小润湿性越好，γ<90°表示该固体表面为亲水表面，反之称为疏水表面。Wang等[24]模拟比较了不同润湿性下（γ=5°、33°、147°、175°）PHP性能，发现γ大的PHP启动时间更短，而小接触角可以提高传热极限防止蒸发段烧干；并在几种润湿性下都观察到了如图13 所示的接触角滞后现象（液柱运动方向一端的接触角γA大于另一端的接触角γR），这证明了管内压降始终为正。战洪仁等[41]对亲水表面下（γ=4.3°、20°、40°、60°、82.5°）PHP进行模拟，同样发现γ大的PHP启动时间短，并且提出γ<40°时流动模式切换频率较快，这说明小接触角更易流动补充烧干部分。

图13 接触角滞后现象[24]

3.6 工质物性

工质对PHP 性能的影响由多个物性参数决定，通常认为相变潜热小的工质热性能更优越[3]。气相密度采用理想气体模型求解、多项式拟合求解或假设为常数；液相为不可压缩流体，密度由温度拟合曲线得出。对于低温工质，气相使用Soave Redlich Kwong实际气体模型求解密度更为准确。

Pouryoussefi 等[38]模拟PHP 运行状态并利用功率谱密度对温度时间序列进行谱分析，发现乙醇有比水更高频率的温度振荡，更有利于热量传递。Pachghare 等[37]模拟了水分别与乙醇、甲醇和丙酮组成的1∶1 二元混合物的PHP，几种二元混合物在低加热功率（8～40W）时热性能皆优于其组分中的纯工质，水的热阻始终高于其他纯工质和二元工质，但这种情况随着加热功率增大不再明显。陈曦等[17,29,31]模拟多种低温工质PHP 发现，由于低温下所需加热功率很小，温度波动幅度远远小于常温PHP下的波动幅度。徐金柱等[25]模拟液氢温区高充液率（80%）PHP 在稳定运行的加热功率（0.27～1W）区间内，温度振荡频率随着加热功率的增加先增大而后趋于稳定。

有的研究者希望通过在工质中加入活性剂或纳米颗粒加快相变，这在模拟中也得到了研究。十六烷基三甲基氯化铵（CTAC）是一种表面活性剂，极少量的CTAC 就能促进相变的发生。Bastakoti 等[19]模拟含2000×10-6CTAC水溶液的PHP，结果发现较低充液率（FR=0.35）会导致烧干，在较高充液率（FR=0.5～0.65）时传热性能优于水。为探究CTAC含量对PHP 启动的影响，Wang 等[20]通过模拟探究不同含量CTAC（50×10-6、100×10-6、2000×10-6）水溶液PHP 的性能，发现50×10-6、100×10-6CTAC 有效缩短了启动时间且降低了启动温度；2000×10-6CTAC 启动阶段温度波动剧烈，启动效果较差。为提升工质的传热极限，避免蒸发段烧干的发生，Li等[21]选用微胶囊相变材料（MEPCM）悬浮液作为工质，相变温度为364～374K的悬浮液通过热吸附作用延缓了温度的升高，传热极限显著提高，但启动时间变长且热阻有所增加。Xu等[33]模拟银纳米流体（质量分数0.25%、0.75%、1%）水溶液的PHP 发现，间歇性流动和不稳定振荡是银纳米流体PHP的主要特征。银纳米流体延长了PHP的启动时间，在高加热功率下仍能保持稳定运行，能有效帮助蒸发段防止烧干。实际上，颗粒流体是复杂的气-液-固三相流动，而上述模拟本质上计算的是改变了物性的均质流体，不分开处理颗粒与基液，这对模拟结果产生的影响仍然未知。

4 结语

PHP的优越性已经得到了广泛的认可，在许多领域有极大的应用潜力。PHP虽然结构简单，但内部存在复杂的气液相流动和换热，理论分析较为困难。目前，通过CFD 模拟来分析PHP 性能的可靠性已经得到了验证，同时还可以获得气液相界面、振荡时压降及两相流型转换等重要信息，为一维数值模拟的发展提供理论支持。本文总结国内外公开发表的CFD 模拟PHP 的研究，得到了以下几个方面的结论。

（1）最普遍的多相流-表面张力-相变模型组合是VOF-CSF-Lee，目前该模型无法对液膜形状和液膜的相变进行有效模拟，其中Lee模型蒸发和冷凝系数的选择尚未有理论依据，主要依靠与实验的对比确定，因此成为制约其应用的主要难点。下一步CFD 模拟需要结合可视化研究，建立PHP 管内的相变模型，进一步提供模拟精度。

（2）关于二维模拟几何模型管径，大多研究者采用实际内径，也有学者通过相似原理分析重力与表面张力的比值来确定内径，两种方式在对应研究中均验证了模拟的有效性，但尚未有研究对比两种方式的影响。下一步，需要对PHP 开展实验和CFD三维和二维模拟的综合分析，明确二维模拟中内径的选择方法。

（3）相关研究已表明有规律地扩缩管径能进一步提高PHP的传热特性；液体与壁面润湿性越好，越有利于预防烧干；加入一定含量的相变颗粒也有助于传热极限的提高。在模拟混合颗粒流体的相关文献中，研究者普遍忽略颗粒固体，仅将工质作为均质流体，这种处理方式的影响仍然未知。对颗粒流体模拟可参考其他多相流模拟文献中耦合离散相模型（discrete phase model, DPM）的方法，明确均质假设对模拟结果的影响。

符号说明