双桅杆式起重机的时变输入整形控制方法

邱泽昊,孙 宁,刘卓清,杨 桐,吴庆祥,方勇纯

(南开大学人工智能学院机器人与信息自动化研究所,天津市智能机器人技术重点实验室,天津 300350)

1 引言

近年来,欠驱动机械系统在工业生产中的应用愈加广泛.为提高生产效率,减少人工操作带来的风险,需设计有效的控制方法,在保证负载运输安全的同时,使负载准确稳定地到达目标位置.然而,由于欠驱动系统包含一些不可驱动的状态变量,导致在设计控制方法时,必须使用较少的控制输入来控制较多的系统自由度.为此,许多学者针对欠驱动机械系统的控制问题展开研究[1-12].其中,欠驱动起重机作为常用的大型运载工具,可根据运动方式分为多种结构类型,包括桥式起重机[13-15]、塔式起重机[16-18]、桅杆式起重机[19-21]等.各类型的起重机具有不同的动力学模型和控制目标,且控制方法也有所区别,但可根据是否存在反馈大致分为输入整形、运动规划等开环控制方法[22-25]和模糊控制、滑模控制、自适应控制等闭环控制方法[26-34]两类.

由上述对各类起重机的研究可以看出,目前针对单起重机系统的研究已经比较成熟,但随着工业生产的发展,单起重机有限的承载能力已不能满足大型负载的吊运需求.因此,需要两台或者多台起重机协同工作以降低单台起重机的承重.这类多起重机系统的动力学特性更为复杂,可能导致针对单起重机的控制方法不再适用.具体而言,双桅杆式起重机作为一种典型的多起重机系统,相较于一般的单起重机系统,状态变量间具有更加复杂的非线性耦合关系.首先,在双桅杆式起重机的运行过程中,两台起重机分别通过各自的吊绳与负载两端相连接,负载在吊臂的协同运动下移动至目标位置,这意味着两台起重机与负载在共同运动时必须视作一个整体.其次,当使用双桅杆式起重机吊运大型负载时,由于负载不能被视作质点,系统模型将含有更加复杂的结构和参数.除此之外,两台起重机协同运动意味着整个系统需要考虑更多的变量和更强的非线性特性,增加了分析和计算的难度.最后,两台起重机通过负载连接在一起,相互制约,限制了彼此的运动范围.因此,在分析时需要充分考虑系统的几何约束.

上述特性使得针对双桅杆式起重机的控制问题研究更具有挑战性.目前,与单起重机系统相比,针对多起重机系统的研究虽然非常有限,但其中也有不少成果具有启发性.文献[35]通过精确的几何分析和数学推导,使用拉格朗日方法建立了双桅杆式起重机的完整动力学模型.文献[36]将多移动式起重机分成执行器末端和移动式起重机本体两部分,对二者的稳定性分别进行分析.此外,双桥式起重机作为一种基础的多起重机系统,与输入整形控制有着良好的结合.文献[37]通过分析线性化的动力学模型,设计了改进的四脉冲极不灵敏型输入整形器,有效地减小了残余振荡.为设计输入整形器,文献[38]使用合理的简化条件削弱了系统的非线性,并对比了不同输入整形器的性能.进一步地,在近期的研究中,Fu等人[39]为双桅杆式起重机系统设计了自适应耦合消摆跟踪控制方法,实现了令人满意的消摆效果.

尽管上述方法对于双桅杆式起重机的研究很有意义,但仍存在着一些亟待解决的问题.

1)现有控制方法大多针对双桥式起重机.相较于双桥式起重机,双桅杆式起重机包含更复杂的旋转运动,而这些旋转运动状态很难被解耦.因此,适用于双桥式起重机的控制方法不能直接应用于双桅杆式起重机.这意味着提出针对双桅杆式起重机的具体控制方法是非常重要的.

2)两台起重机通过负载和吊绳相连接,组成的系统具有强耦合性,在共同运动时必须被视作一个整体.然而,一些研究为简化分析,将整个系统进行拆分,这样可能会导致设计不严密,产生不理想的控制效果.

为实现对双桅杆式起重机的消摆控制,本文通过分析系统的几何约束与动力学模型,推出状态变量及其高阶导数之间的关系.随后,基于严密的数学推导,合理变换了双桅杆式起重机的动力学模型,得到吊臂俯仰角和负载姿态角之间的动力学关系.在此基础上,计算出系统的时变振荡周期,设计一种极不灵敏型输入整形器.最后,使用双桅杆式起重机实验平台进行实验,验证所提时变输入整形控制方法的有效性.

本文剩余内容包含如下部分: 第2节讨论系统动力学模型和控制目标;通过严密的数学推导,将在第3节给出一种采用时变振荡周期的极不灵敏型输入整形器的分析设计过程;第4节将进行一系列实验,以验证所提时变输入整形控制方法的有效性;第5节将对全文工作进行总结.

2 问题描述

本节将分别对系统的几何约束、动力学模型和控制目标进行描述.

2.1 动力学模型

通过分析如图1所示双桅杆式起重机在水平和竖直方向上的几何位置关系,可得如下几何约束1为使表达更加简约,本文将所用三角函数表达式简写为如下形式:

:

图1 双桅杆式起重机模型Fig.1 Model of dual boom cranes

在式(1)中:H表示O1O2的长度,即两台起重机之间的距离;2h是P1P2的长度,即负载两个悬挂点之间的距离;l表示B1P1和B2P2的长度;L是O1B1和O2B2的长度.此外,α1(t)和α2(t)表示吊臂俯仰角;θ1(t)和θ2(t)是负载沿吊绳的摆角,无法被电机直接驱动;θ3(t)是P1P2和竖直方向的夹角,代表负载的姿态角.作为非独立状态变量,θ2(t)和θ3(t)可表示为θ2=β(α1,α2,θ1)和θ3=σ(α1,α2,θ1).角的方向均在图1中标出.图1中其他状态变量和参数的含义见表1.

表1 变量和参数Table 1 Variables and parameters

根据图1所示双桅杆式起重机模型,系统动能可以具体表示为

进一步地,系统势能可以表示为如下形式:

接下来,本文将主要分析动力学模型中的欠驱动部分,以获取系统的振荡特性.基于拉格朗日动力学分析,可推得欠驱动部分的动力学模型如下:

其中:βθ和σθ可由非独立变量θ2(t)和θ3(t)推出,即

基于系统动能和势能,γ1,γ2和γ3可利用拉格朗日方程计算得到,其具体表达式为

为进一步分析式(2),由起重机的实际作业情况可知,两台起重机的吊臂运动状态相同,即α1=α2=α和同时,起重机在实际作业时移动缓慢,负载的摆角及变化很小.因此,双桅杆式起重机为对称系统.综上,可得如下假设:

假设1θ1和-θ2相等,θ3约等于π/2.

假设2式(2)中的部分变量和参数具有如下关系:

至此,双桅杆式起重机的动力学模型得以推出,其中部分变量和参数的假设关系也基于实际作业情况计算给出.

2.2 控制目标

作为一种对称系统,当双桅杆式起重机处于稳定状态时,期望的控制目标可以具体表述如下:

·负载在控制器的作用下,于时刻Tm到达目标位置.其中,θ1,θ2和θ3与目标位置的距离尽可能小,吊臂俯仰角的状态为

3 模型分析与控制器设计

3.1 模型分析

为计算系统的振荡周期,需推出系统的输入输出关系.为此,需将系统的动力学模型整理为如下形式:

其中:Vi代表输入变量,Vo代表输出变量.根据双桅杆式起重机的实际结构,吊臂俯仰角α是由电机直接驱动的,可视为输入变量;负载姿态角θ3能体现负载的摆动情况,可视为输出变量.因此,式(4)可改写为

通过比较式(2)与式(5)可看出,式(2)中存在众多干扰状态变量及其导数.为由式(2)推得如式(5)所示形式的方程,需找出干扰状态变量与所需状态变量及其高阶导数之间的关系,以实现对干扰状态变量的消除.具体而言,分为如下3个步骤:

步骤1首先,计算吊绳摆角θ1,θ2与负载姿态角θ3及其高阶导数之间的关系.

对式(1)进行变换可推得如下方程:

通过重新整理式(6),可以得到如下结果:

接下来,对式(1)求二阶导可得

于是,可以构造如下方程:

步骤2其次,进一步计算θ1,θ3与α高阶导数之间的关系.

对式(3)求导可得

步骤3最后,对双桅杆式起重机欠驱动部分的动力学模型式(2)进行整理.

将式(8)和式(10)代入式(2)可得

将θ4与式(7)代入式(11),进一步计算可得

为揭示吊臂俯仰角α与负载姿态角θ4之间的关系,将式(12)中各变量的系数依次替换为Q1,Q2和Q3可得

至此,式(13)与式(5)的形式相同,可求解系统的振荡频率为

最终,双桅杆式起重机的系统振荡周期可计算如下:

在式(14)中,当吊臂与负载共同运动时,Bd的大小不断变化.因此,由式(14)计算得到的系统振荡周期T是时变量.这意味着双桅杆式起重机的系统振荡周期是随着负载吊运过程中系统运动姿态的变化而改变的,即双桅杆式起重机具有时变振荡特性.

3.2 控制器设计

输入整形控制[40-42]是一种前馈控制方法.它通过分析被控系统的振荡特性,设计一系列具有不同幅值和时延的脉冲信号,在与原始输入信号卷积后,使它们的残余振荡相互抵消,最终达到消摆目的.其中,极不灵敏型输入整形器具有强鲁棒性和良好的消摆性能.它主要由3个脉冲组成,每个脉冲的时延由被控系统的振荡周期决定,幅值则受所允许的残余振荡调整.

由于双桅杆式起重机的复杂模型拥有大量的状态变量和参数,设计的输入整形器必须具备针对模型不准确的鲁棒性.同时,大质量、大体积的负载吊运也需优先考虑控制的稳定性.结合式(14)所计算的振荡周期T,设计具有如下形式传递函数的极不灵敏型输入整形器:

其中:Ai为各脉冲幅值,ti为各脉冲延时.设定系统允许的残余振荡比例为Ve,可得如下关系式:

由式(15)可解得各脉冲幅值,并设计如下极不灵敏型输入整形器[43]:

结合式(14)和式(16),可得如图2所示的所提时变输入整形控制的流程.相较于普通的输入整形控制,所提方法基于反馈得到的双桅杆式起重机运动姿态,通过式(14)计算该运动姿态的振荡周期,实时输入到式(16)中形成对应的输入整形器,最终完成消摆控制.此过程具备对双桅杆式起重机运动姿态变化的鲁棒性,避免预计算振荡周期的局限性.

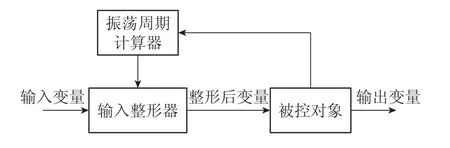
图2 所提时变输入整形控制Fig.2 Proposed time-varying input shaping control

4 实验结果与分析

本节将基于自搭建的双桅杆式起重机实验平台,针对双桅杆式起重机进行3组实验,以验证所提控制方法的消摆性能和鲁棒性.

如图3和图4所示,实验平台主要由两台自主搭建的桅杆式起重机、上位计算机、运动控制器、包含内部编码器的伺服电机(精度:2500 PPR)和角度编码器(精度:1000 PPR)组成.其中,桅杆式起重机的机械部分主要包括吊臂、负载和吊绳,它们能实现吊臂俯仰、负载摆动等桅杆式起重机的主要运动.

图3 自搭建双桅杆式起重机实验平台Fig.3 Self-built dual boom cranes experimental platform

图4 实验平台控制系统Fig.4 Control system of the experimental platform

在实验平台中,为保持仿真与实验软件环境的连续性,实现算法与控制硬件的有效连通,控制算法由运行在上位计算机中的MATLAB/Simulink实时窗口执行(控制周期:5 ms).它产生的控制信号通过运动控制器传输到电机驱动器并驱动电机转动,在电机的转动作用下,吊臂俯仰角发生变化,连接吊臂和负载的吊绳出现摆动.其中,吊绳摆角由角度编码器测量,吊臂俯仰角则由电机内部的编码器测量,二者测量得到的值均通过运动控制器反馈回上位机.可以看出,整个实验平台具有模拟实际、控制运动、采集信息、反馈信息等功能,其机械结构和控制系统都是易于开发和移植的.

实验平台相应的物理参数为

不失一般性地,将两台起重机的初始状态设置为

此外,选择吊臂的期望轨迹为

根据吊臂的期望轨迹和系统的几何约束,可以计算得到目标位置为

考虑起重机的实际作业需求,设定系统允许的残余振荡比例为

在完成系统参数的设定后,为具体描述系统的残余振荡,提出如下评价指标:

其中:θ1(t)up表示θ1(t)的局部极大值,即θ1(t)在上一时刻增大,下一时刻减小;θ1(t)down表示θ1(t)的局部极小值,即θ1(t)在上一时刻减小,下一时刻增大;tmax为系统的总运行时间;t>tmax/2保证θ1在接受评价时已经进入残余振荡状态;=0则为保证负载已经到达目标位置;max{θ1(t)up-θ1(t)down}为残余振荡幅度的最大值,能够充分体现系统的振荡特性.

为体现本文所计算振荡周期的准确性和时变特性以及所提控制方法的有效性,基于完全相同的极不灵敏型输入整形器,首先,将所提方法与未使用输入整形器和使用双桅杆式起重机固定位置振荡周期的输入整形器情况进行对比.随后,通过在实验中修改吊绳长度和负载质量,进一步验证本文方法对系统参数的鲁棒性.下面是3组具体实验.

实验1本组实验将未经过输入整形、经过本文所提输入整形器整形和经过使用双桅杆式起重机固定位置振荡周期的输入整形器整形的系统性能进行对比.双桅杆式起重机在运行过程中某个固定位置的振荡周期Ts可由式(14)计算得到.不失一般性地,本文选择

如图5所示,在使用输入整形器前,θ1,θ2和θ3都存在明显的大幅摆动,无法准确地稳定在目标位置.其中θ1R(t)的值为3.08◦.

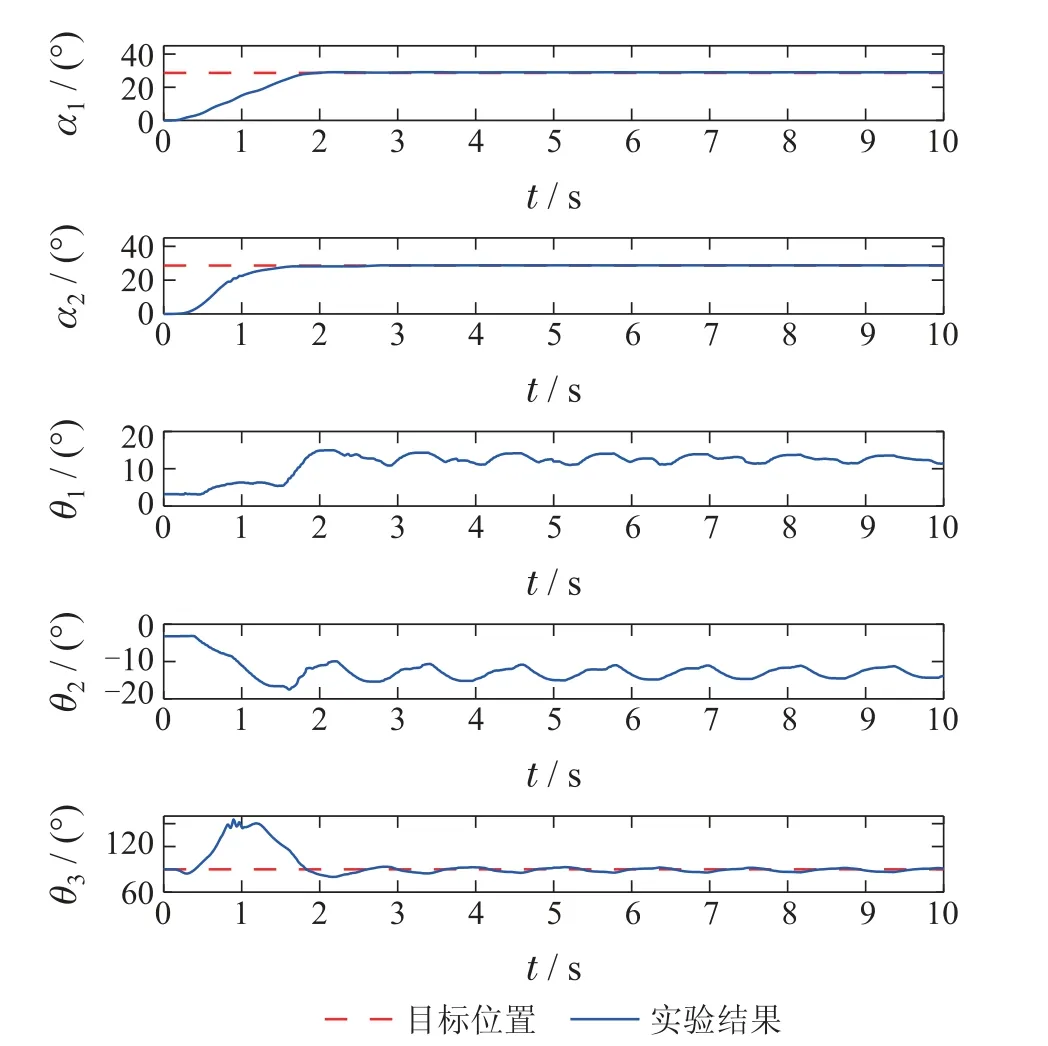
图5 实验1: 未经过输入整形的实验结果Fig.5 Experiment 1: experimental results without input shaping

如图6中的实线所示,在使用本文所提输入整形器后,相较于未经输入整形的结果(见图5),吊臂俯仰角的定位依然准确,θ1,θ2和θ3的摆动幅度显著减小.具体而言,θ1R(t)的值为0.14◦,降低为输入整形前的4.5%,这意味着输入整形后负载的摆动得到显著抑制.

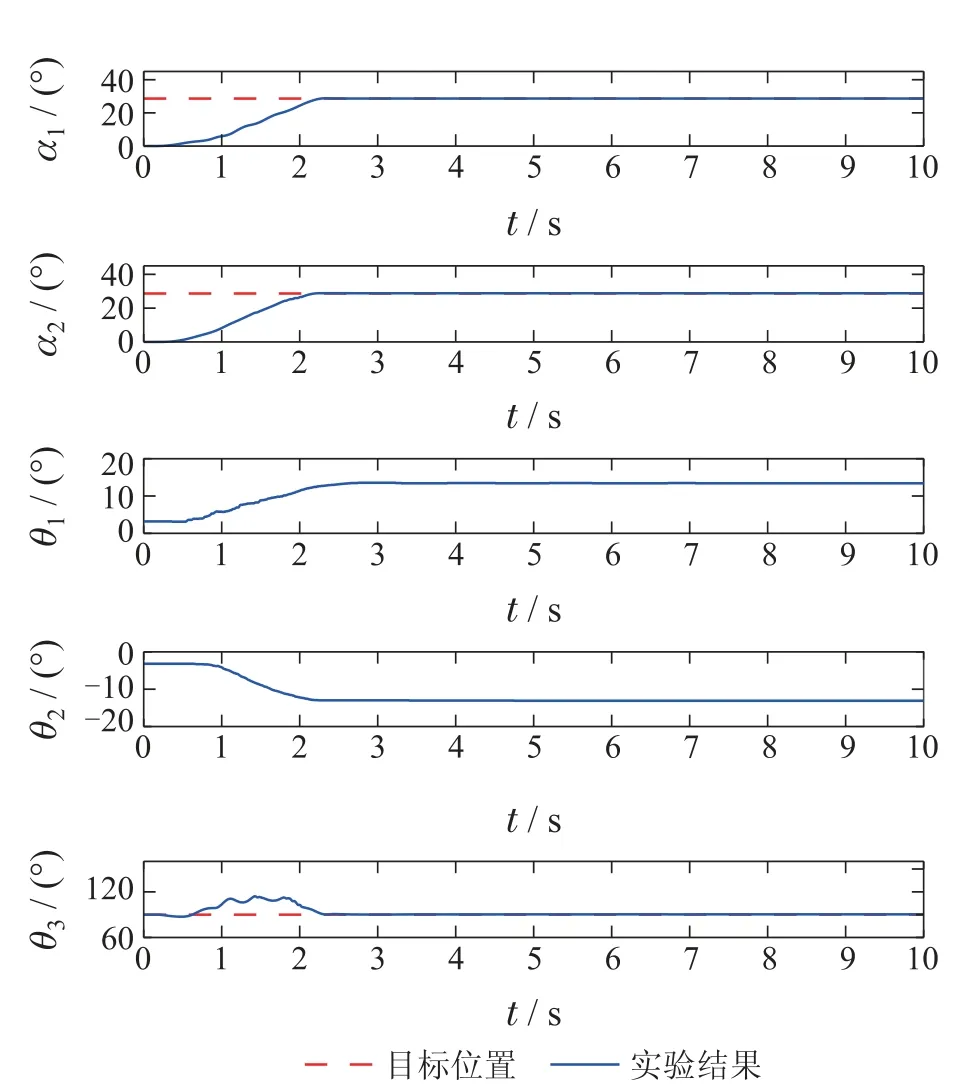
图6 实验1: 本文所提方法的实验结果Fig.6 Experiment 1: experimental results of the proposed method

在图7中,输入整形器使用双桅杆式起重机固定位置振荡周期,虽然具有一定的消摆效果,θ1R(t)降低到1.74◦,为输入整形前的56.5%,但远不如本文所提输入整形器的消摆效果令人满意(见图6).因此,所计算的时变振荡周期比双桅杆式起重机运动过程中的某个固定振荡周期更准确,体现振荡周期时变的必要性.使用该时变振荡周期的输入整形器在保证定位准确的同时,具有令人满意的消摆能力.

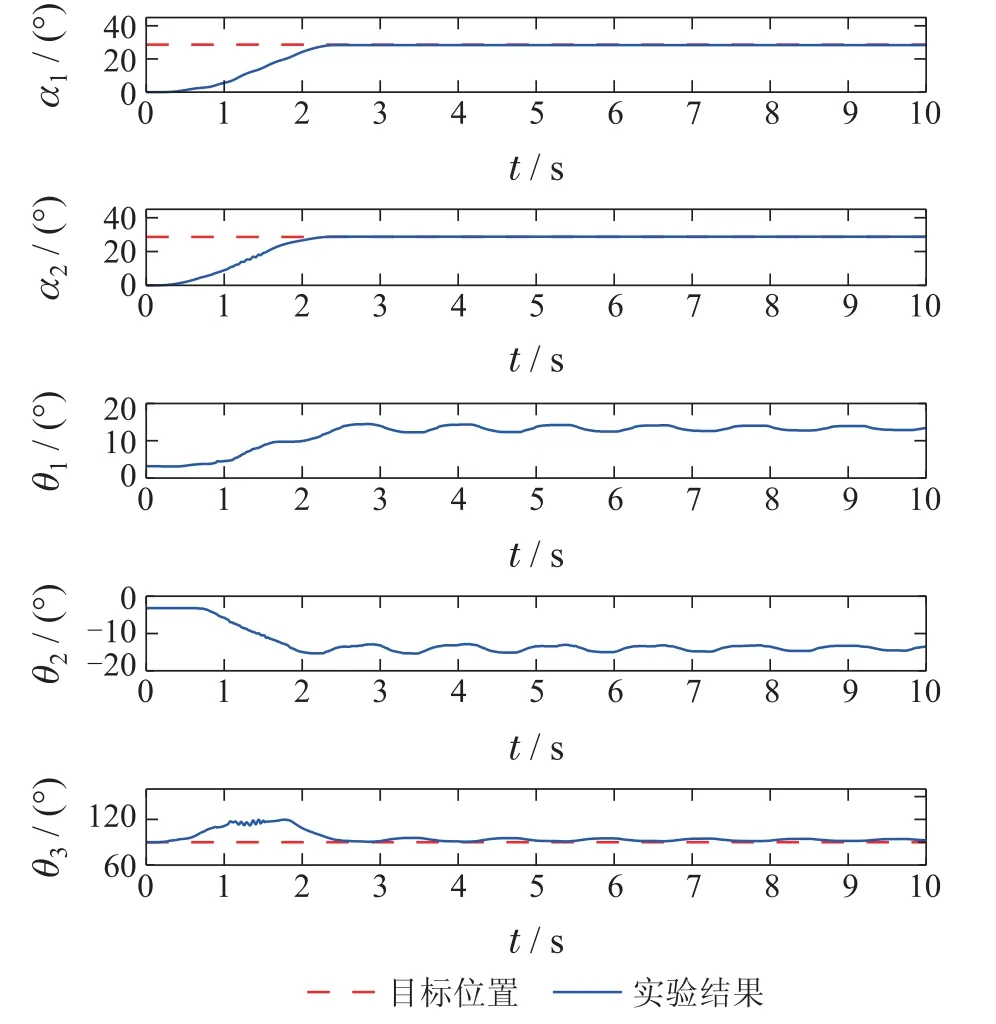
图7 实验1: 经过使用双桅杆式起重机固定位置振荡周期的输入整形器整形的实验结果Fig.7 Experiment 1: experimental results of the input shaper using the oscillation period of DBCs at a fixed position

实验2双桅杆式起重机工作时,经常需要运送不同负载,导致负载质量发生变化.同时,根据式(14),系统振荡周期的计算中不涉及负载质量m.从理论层面看,负载质量的变化应对实验结果影响不大.因此,本组实验将负载质量由0.8 kg增加至1.1 kg,以验证本文方法对负载质量参数变化的鲁棒性.

由图8可以看出,在负载质量发生变化后,θ1,θ2和θ3的振荡特性与变化前有所区别且存在明显摆动,但如图9所示,本文所提输入整形器仍然显著地消除了θ1,θ2和θ3的摆动.因此,本文所提控制方法对负载质量参数的变化具有良好的鲁棒性.

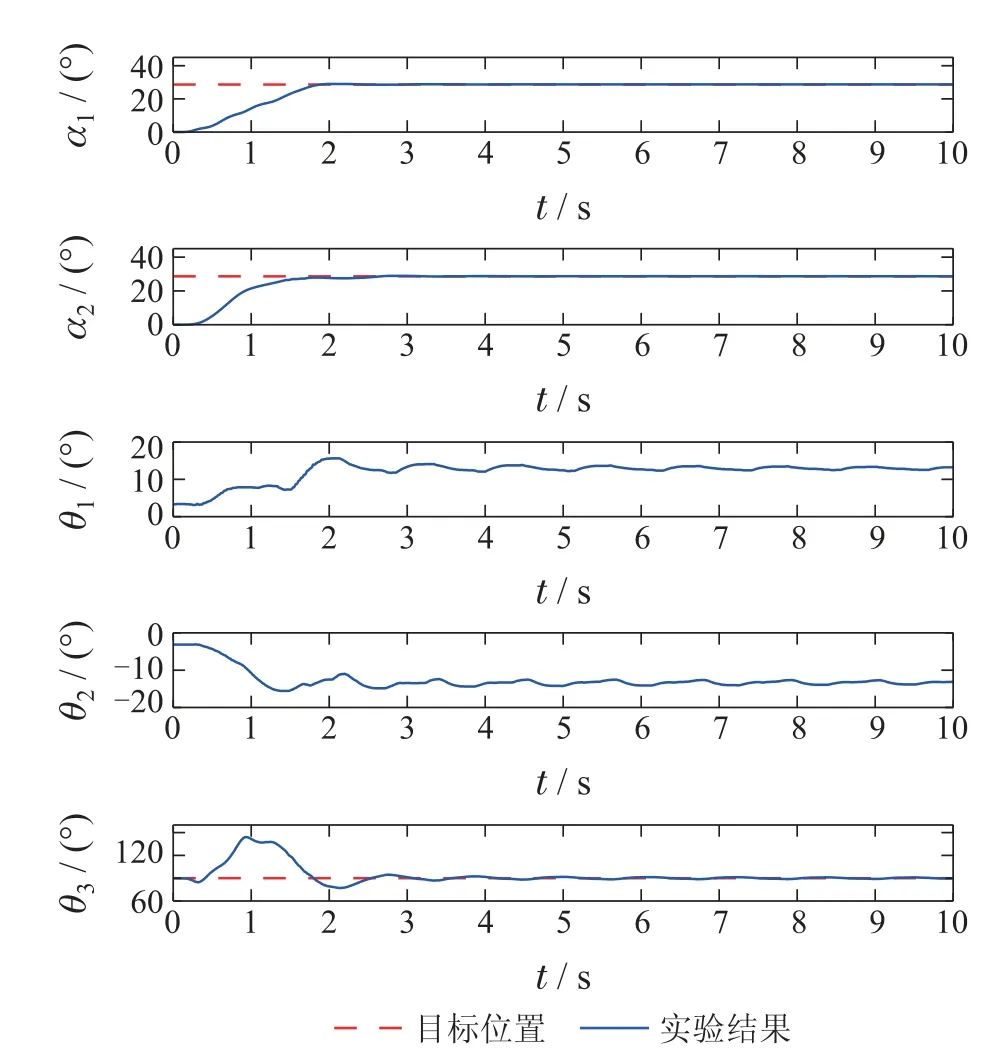
图8 实验2: 负载质量调整为1.1 kg,未经过输入整形的实验结果Fig.8 Experiment 2: experimental results without input shaping after changing payload mass to 1.1 kg

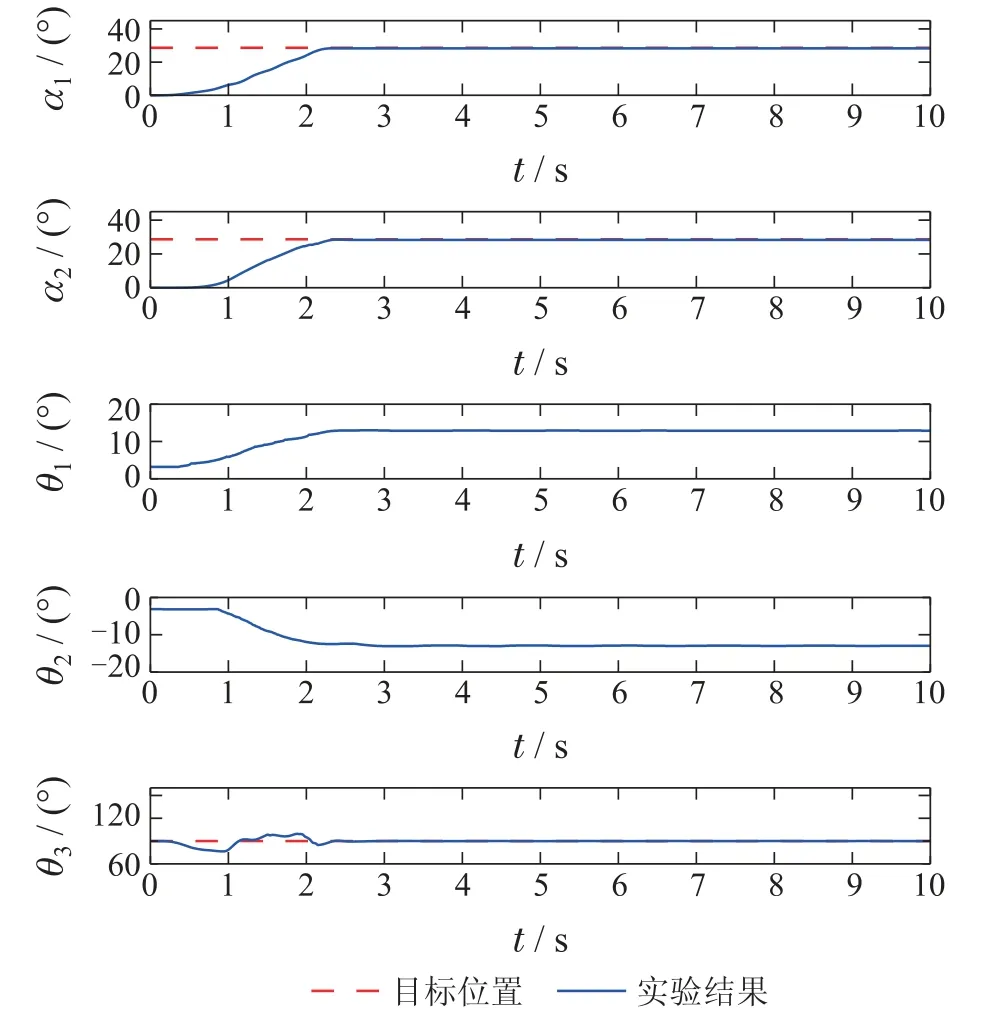
图9 实验2: 负载质量调整为1.1 kg,本文所提方法的实验结果Fig.9 Experiment 2: experimental results of the proposed method after changing payload mass to 1.1 kg

实验3在实际作业中,双桅杆式起重机需要通过改变吊绳长度将负载运送至不同位置.同时,式(14)中的系统振荡周期随吊绳长度的变化而改变,而所提时变输入整形控制对系统的不同振荡特性都应具有消摆作用.因此,本组实验将吊绳长度由0.45 m增加至0.60 m,以验证所提方法对吊绳长度参数变化的鲁棒性.

在吊绳长度发生变化后,θ1,θ2和θ3在未经整形时仍有大幅摆动(见图10).本文所提输入整形器则保持了对θ1,θ2和θ3摆动的消除作用,几乎没有受到参数变化的影响(见图11).因此,本文所提控制方法对吊绳长度参数的变化同样具有良好的鲁棒性.

图10 实验3: 吊绳长度调整为0.60 m,未经过输入整形的实验结果Fig.10 Experiment 3: experimental results without input shaping after changing rope length to 0.60 m

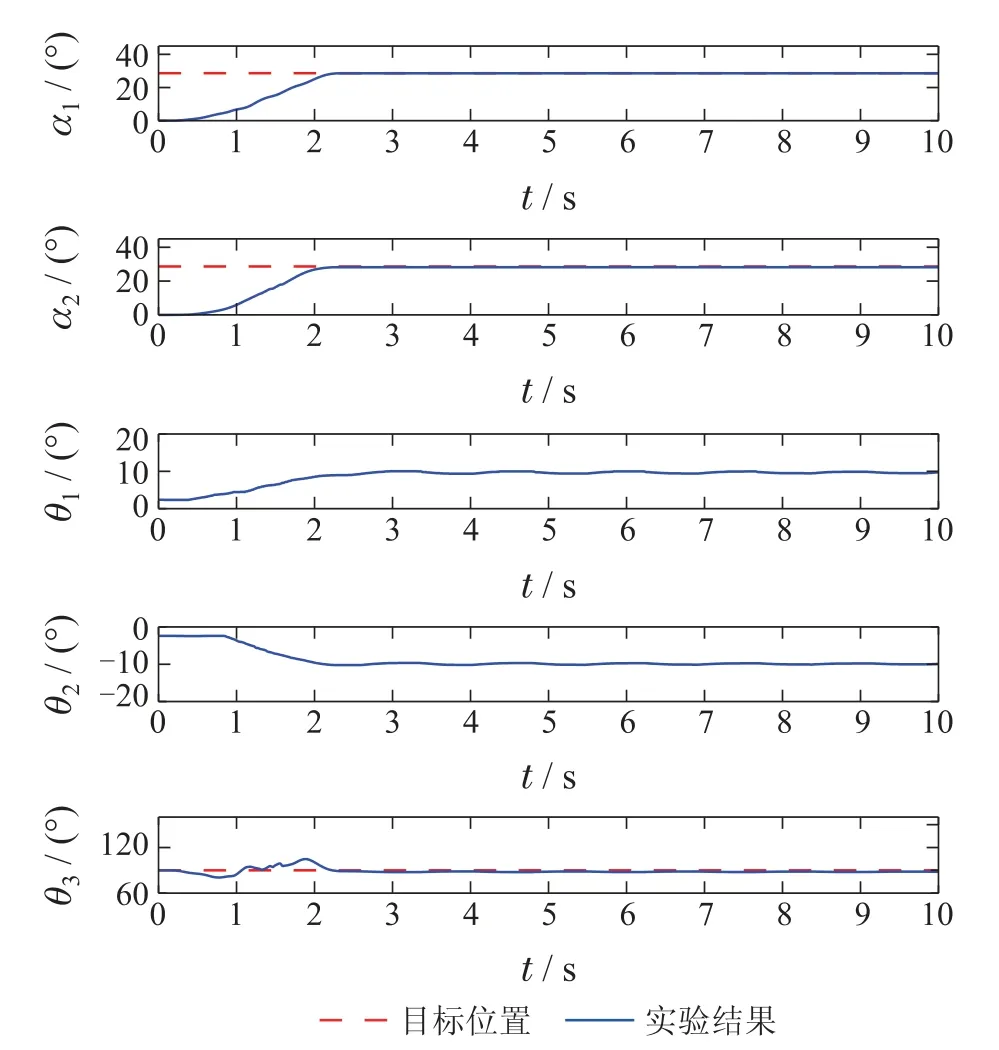
图11 实验3: 吊绳长度调整为0.60 m,本文方法的实验结果Fig.11 Experiment 3: experimental results of the proposed method after changing rope length to 0.60 m

5 结论

为实现对双桅杆式起重机的消摆控制,本文提出了一种时变输入整形控制方法,同时实现了起重机的精确定位和对负载摆动的消除.基于系统的几何约束、动力学模型和实际作业情况,推导出状态变量及其高阶导数之间的关系,对系统模型的形式进行了变换.此外,本文还通过分析双桅杆式起重机的动态特性,计算出系统的时变振荡周期,并设计一种极不灵敏型输入整形器.基于上述内容,设计并进行了3组实验,验证了所计算时变振荡周期的准确性、所提输入整形器的有效性和对参数的鲁棒性,表明所提出的针对双桅杆式起重机的时变输入整形控制方法具有令人满意的消摆性能.考虑输入整形控制的时延问题和自身结构的局限性,为实现对双桅杆式起重机更好的控制效果,将在未来的研究中设计更先进的控制方法,以平衡输入整形控制的时延和稳定性,提升系统对外界扰动的鲁棒性.