具有扩散项和Lévy噪声的随机年龄结构种群系统的指数稳定性

韩 婷,李国平†,马维军

(1.宁夏大学新华学院,宁夏银川 750021;2.宁夏大学信息工程学院,宁夏银川 750021)

1 引言

生物种群模型主要用于研究种群的密度和数量的发展规律,是当今社会科学和自然科学研究中的重要课题.对种群模型的研究,有助于理解种群系统的动态特性,为短期和长期预测种群数量,发现种群控制规律和制定生物保护政策提供严格的数学基础和新的计算方法.研究过程中不仅要考虑随时间的变化规律,还需考虑种群的年龄、外界环境、空间分布等因素的影响.因此建立合适的种群系统具有重要的理论价值和现实意义.事实上,学者根据不同生物群体,已建立许多种群数学模型,包括确定性种群系统和随机种群系统.

常用的确定性模型有Malthus 模型和Logistc 模型[1].由于不同年龄的种群的生物学特征有着明显差异,文献[2]在上述模型基础上给出了具有年龄结构的种群模型

其中:a表示年龄,t表示时间,β(t,a)表示种群在年龄a时的生育率,µ(t,a)表示种群在年龄a时的死亡率,N(t,a)表示时刻t年龄为a的种群密度.种群在生长的过程中会出现迁徙现象.文献[3-4]建立了具有扩散项的年龄结构的种群模型以刻画该现象.

现实世界中,种群还受外界随机因素的影响.一方面种群会经常受环境噪声的干扰.由Brown运动驱动的具有扩散的随机年龄结构种群系统已受到广泛关注.一个经典的具有扩散项的年龄结构随机种群系统可以表示为

其中:A>0,x∈X ⊂Rn(1≤n≤3),J=(0,A)×X,分别表示时刻t年龄为a的种群在空间x的密度、生育率和死亡率,∆表示关于空间变量x的Laplace算子,k(t,a)>0是扩散系数,f(t,N)表示外部环境对种群系统的影响,g(t,N)表示Brown噪声的密度.许多学者从不同角度讨论了该系统的性质[5-9].其中文献[5]研究了具有年龄结构的随机种群系统解的存在性、唯一性与指数稳定性.文献[7]考虑了具有年龄结构随机种群系统的半隐式Euler法的数值解的均方收敛性.

另一方面,种群可能会受到地震、飓风、传染病爆发、有毒污染物泄露等一些突发性大的随机扰动,如COVID-19对人类造成的影响.为描述此类现象在系统(2)中引入Lévy噪声更加符合实际情形.因此本文研究如下具有扩散项和Lévy噪声的随机年龄结构种群系统:

其中:h(t,N,u)表示Lévy噪声的强度,(dt,du)=P(dt,du)-ν(du)dt是与B(t)独立的Poisson补偿过程,P(dt,du)表示在可测集U上具有有限特征测度ν的Poisson计数测度.关于由Lévy过程驱动的随机微分方程理论相对成熟[10-18].然而,将Lévy过程引入到随机年龄结构种群系统中的研究较少.文献[10]讨论了由Lévy过程驱动的随机种群系统的解的存在性及渐近性质.

事实上,自然环境中各种随机因素对种群系统稳定性的影响较大,而系统的稳定性为种群系统的最优控制、数值解的收敛性等研究奠定了基础,对生物资源的可持续发展和利用也起着决定性作用.因此对系统(3)稳定性的研究尤为重要.目前,稳定性理论的内容得到了不断扩大和完善.文献[19]给出了混合随机微分方程稳定性的充分条件.文献[20]讨论了具有大脉冲时滞的线性脉冲系统的稳定性.但关于随机年龄结构种群系统的稳定性的研究较少,且研究方法主要采用Lyapunov方法[7,9,21-22]和Coercivity条件[5,14]等.

基于以上讨论,本文主要研究具有扩散项和Lévy噪声的随机年龄结构种群系统的指数稳定性.本文的创新如下:

1)构建了具有扩散项和Lévy噪声的随机年龄结构种群系统.该系统对种群可能会受到如地震、飓风、传染病爆发、有毒污染物泄露等一些突发性的随机现象的描述更具现实意义;

2)通过能量等式的方法,给出了新的解的指数稳定性和几乎必然指数稳定性的充分条件.

2 预备知识

其中V ∗是V的对偶空间.用‖·‖,|·|和‖·‖∗分别表示空间V,H和V ∗上的范数,用〈·,·〉表示对偶空间V和V ∗的内积,(·,·)表示空间H上的内积,l是正常数使得对任意x ∈V都有|x|2≤l‖x‖2.

令(Ω,F,P)是具有滤波{Ft}t≥0(满足通常的条件:单调递增且右连续;F0包括所有P-零测集)的完备概率空间.B(t)是定义在该空间上的Wiener过程,在可分的Hilbert空间K中取值且具有增量协方差算子Q.G ∈L(K,H)是从K到H的所有有界线性算子构成的空间,‖G‖2表示其Hilbert-Schmidt 范数,即

由文献[22],系统(3)的能量等式定义如下:

定义1设N(t)是定义在概率空间(Ω,F,P)上Ft适应的随机过程,若满足以下条件,则N(t)称为系统(3)的能量解:

1)N(t)∈I2([0,T];V)∩L2(Ω;C([0,T];H)),T>0;

2)对任意的t∈[0,T],下列方程在空间V ∗上几乎必然成立:

3)对任意的t∈[0,T],下列能量等式成立:

定义2如果系统(3)的能量解N(t)满足下列不等式:

其中:α>0,C=C(N0)>0,则系统(3)的能量解N(t)当t →∞时均方指数收敛于零.进一步,如果任意一能量解当t →∞时均方指数收敛于零,并且零是系统(3)的解,则该零解在均方意义下指数稳定.

定义3如果存在正常数C=δ(ϵ)>0,α>0和Ω0⊂Ω,N(Ω0)=0,并且对于每个ω ∈Ω-Ω0,都存在正的随机数T(ω)使得

则称系统(3)的能量解N(t)当t →∞时几乎必然指数收敛于零.进一步,如果任意一能量解当t →∞时几乎必然指数收敛于零,并且零是系统(3)的解,则该零解几乎必然指数稳定.

引理1[23-24]令θ=1或2.假设h1:R+×U →H(R+=[0,∞))是可测函数且满足

为了研究系统(3)的稳定性,假设以下条件成立:

假设1f(t,0)=0,g(t,0)=0,h(t,0)=0.

假设2存在常数k1,k2,k3>0使得对任意N1,N2∈C,下列不等式成立:

假设3µ(t,a,x),β(t,a,x)在R+×连续,k(t,a)在R+×(0,A)连续,且

注1由假设1-3并应用文献[5]的方法,易证系统(3)存在唯一解.本文在系统(3)存在唯一解的基础上进一步讨论系统的稳定性.

3 能量解的指数稳定性

本节主要讨论系统(3)能量解的均方指数稳定性和几乎必然指数稳定性.下面,首先给出均方指数稳定性的结果.

定理1若假设3-6成立,且

则对于系统(3)的任意能量解N(t),都存在α∈(0,ρ)和C=C(N0)>0使得

即系统(3)的能量解N(t)在均方意义下指数稳定.

证取α∈(0,ρ)使得

将能量等式用于eαt|N(t)|2可得

根据文献[14]的引理1有

由假设3和式(7)可得

由假设4-6和式(6)可得

下面分3种情形进行讨论:

情形1当γ1(s)≤0,γ2(s)≤0或γ1(s)>0,γ2(s)<0时,则式(5)成立.

情形2当γ1(s)<0,γ2(s)>0时,由Gronwall不等式则式(5)成立.

情形3当γ1(s)>0,γ2(s)>0时,利 用Gronwall引理可得

综上可得,存在正实数C=C(N0)>0使得

证毕.

注2定理1给出了随机年龄结构种群系统(3)均方指数稳定性的充分条件.该结果表明,系统的稳定性与种群系统的生育率β(t,a,x),死亡率µ(t,a,x)、扩散系数k(t,a)、外界环境的影响f(t,N)、Brown噪声的密度g(t,N)以及Lévy噪声的强度h(t,N,u)有关.即当上述参数满足假设3-6时随机年龄结构种群系统在均方意义下指数稳定.

定理2假设定理1的条件成立,则存在T(ω)>0使得对所有t>T(ω),下式依概率1成立:

即系统(3)的能量解N(t)几乎必然指数稳定.

证令m≥1是任意给定的自然数,令

由于N(t)是系统(3)的能量解,因此对于任意t∈[m,m+1]都有

根据引理1、假设3和式(7)以及文献[6]可知存在常数c1>0使得

根据Burkholder-Davis-Gundy不等式,可得

由引理1可知存在常数c2>0使得

由假设4-6易得

将式(9)-(11)代入式(8)并结合式(4)有

显然,由假设3-6可知k(t)和l(t)是有界函数,故存在常数C1>0使得

结合式(12)-(13)可得

由Chebyshev不等式,对于任意固定的正实数ϵm都有

最后,根据Borel-Cantelli引理,存在T(ω)>0对所有t>T(ω)几乎必然有

证毕.

注3定理2应用引理1、Burkholder-Davis-Gundy不等式、Chebyshev不等式并在定理1的条件下,从理论上给出了随机年龄结构种群系统(3)的能量解的几乎必然指数稳定的充分条件.

注4事实上,对于一般的随机非线性系统很难构造合适的Lyapunov函数来讨论系统的稳定性,尤其是随机非线性偏微分方程.此外,文献[5,14]中的Coercivity条件较强.因此,如何选择合适的方法来研究随机年龄结构种群系统(3)的稳定性尤为重要.定理1和定理2应用了随机能量等式的方法,即对系统(3)的能量等式的系数函数进行估计,得到系统能量解的稳定性的条件.该方法用于讨论随机非线性系统的稳定性较为有效.

4 例子

下面给出例子说明上述结论的有效性.

考虑如下具有扩散项和Lévy噪声的随机年龄结构种群系统:

显然,假设3-6以及式(4)满足.因此,由定理1-2可得,系统(14)的能量解指数稳定且几乎必然指数稳定.

对于一般的随机微分方程很难求出其解析解,下面运用Euler方法对上述例子的能量解进行数值模拟.

在系统(14)中选取满足条件的系数函数k(t,a)=a2,µ(t,a,x)=β(t,a,x)=1/2(1-a)2,f(t,N)=1/2tN+e-a2t,g(t,N)=(1+1/2t)N,h(t,N,u)=sinN,N0=e-1/(A-a).分别采用半隐式Euler法和隐式Euler法对能量解进行数值模拟,结果如图1-2所示.从图中可看出,受Lévy噪声的影响,种群密度的局部变化差异明显.随着种群年龄增长及时间变化,种群密度逐渐趋于平稳.

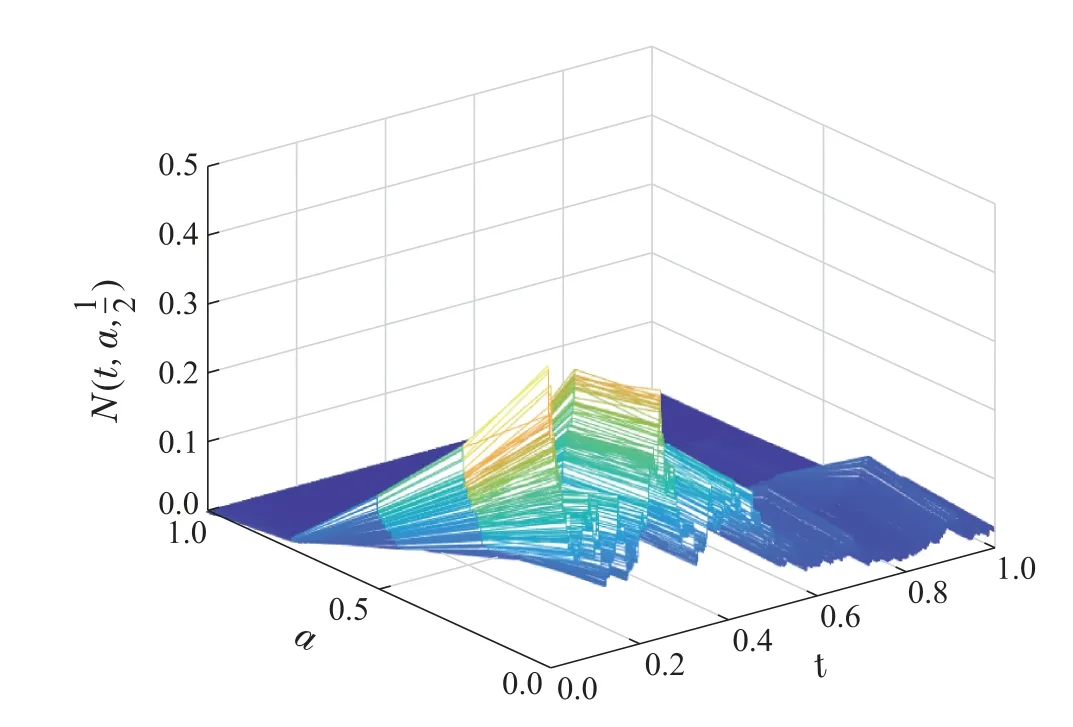
图1 半隐式Euler数值模拟结果Fig.1 Semi-implicit Euler numerical simulation results

图2 隐式Euler数值模拟结果Fig.1 Implicit Euler numerical simulation results

5 结论

为了研究随机环境对生物种群的影响,本文讨论了具有扩散项和Lévy噪声的年龄结构随机种群系统.运用Burkholder-Davis-Gundy不等式、Chebyshev不等式等分析工具对系统的能量等式中的系数函数进行估计,给出了新的解的指数稳定性和几乎必然指数稳定性的充分条件,并结合具体例子及其数值模拟加以验证.该方法不仅有效解决了研究非线性系统的稳定性及控制问题中构造合适的Lyapunov函数时的困难,同时又避免使用较强的Coercivity条件,对于研究随机非线性系统的稳定性较为有效.此外,本文的方法亦可用于讨论随机时滞年龄结构种群系统的稳定性和数值解的稳定性,为随机微分方程的稳定性问题的研究提供了理论依据,对生物资源的可持续发展和利用具有指导意义.