永磁同步电机模型预测转矩控制模糊排序法研究

李耀华,秦 辉,苏锦仕

(长安大学汽车学院,陕西西安 710064)

1 引言

有限状态集模型预测控制(finite control set-model predictive control,FCS-MPC)遍历逆变器所有的开关状态对系统状态进行预测,然后通过设计的成本函数对这些开关状态进行评估,在线求解出最优电压矢量对系统施加控制.近年来,有限状态集模型预测控制在永磁同步电机(PMSM)控制领域也受到了广泛关注[1-9].

成本函数作为评价施加电压矢量作用效果的唯一定量指标,具有较大的柔性,可在一个成本函数体现多个不同控制目标的控制效果,如:磁链、转矩、开关次数等.当成本函数中的控制变量均为同一量纲的物理量,如:定子电流的dq轴分量,成本函数可直接将控制分量相加.但如果控制变量为不同量纲的物理量,如:磁链和转矩,由于磁链控制分量与转矩控制分量不能直接相加,需要通过权重系数实现两者的平衡.

权重系数的设计和调节是模型预测控制的难点,目前常用试验法通过比较不同权重系数的控制效果获取合适的权重系数[10-11].由于权重系数变化范围宽且连续,传统试验法工作量较大.文献[12-15]将模糊控制引入至权重系数的设计和调整中,取得较好的效果.为了避免权重系数的设计,文献[16-17]将磁链和转矩转换为两者的相对误差率,统一了控制变量的量纲.但如果控制目标增加开关次数控制,由于无法将开关次数控制作相应的转换,依然需要权重系数.文献[18-19]通过无差拍控制可将磁链控制和转矩控制转换为理想电压矢量在不同坐标系的投影分量的控制,从而转换为相同量纲的物理量控制,但无差拍控制计算较为复杂,且同样如果增加开关次数控制,也依然需要加入权重系数.文献[20-22]采用神经网络算法或粒子群算法实现权重系数的自整定,但存在需要构造大量训练数据集和算法计算量大的问题.文献[23-24]将多目标决策理论中的VIKOR(vlseKriterijumska optimizacija I kompromisno resenje,折中妥协法)和TOPSIS(technique for order of preference by similarity to ideal solution,优劣解距离法)引入至成本函数,以消除权重系数,但实现较为复杂.文献[25-27]提出排序法的成本函数,将不同量纲的控制变量转换为无量纲的排序结果,可实现多目标控制,但文献并未讨论排序过程最优电压矢量不唯一的情况.传统排序法本质上将所有控制目标的重要性始终视为相同.但实际上,电机系统各个控制目标的重要性并不完全相同,且随着系统状态实时变化.因此,排序法需要考虑实际系统中不同控制目标重要程度的差异性和时变性.

本文基于定子磁链坐标系的表面式永磁同步电机模型预测转矩控制系统,针对磁链和转矩控制与开关次数控制不同量纲的多目标控制问题,采用排序法对控制目标进行独立评价,并设计优先级解决排序过程中最优电压矢量不唯一的问题.针对传统排序法将重要性不同的控制目标相同对待的问题,本文提出了缩放因子来调节控制目标重要性,并对缩放因子的作用效果进行了研究,发现不同于连续变化的权重系数,缩放因子的取值范围是离散有限的,从而大为简化缩放因子的设计和调整.针对控制目标重要性时变问题,本文采用模糊控制基于系统状态动态调整缩放因子.仿真验证了本文提出的基于模糊排序法永磁同步电机模型预测控制的可行性和优越性.

2 传统模型预测转矩控制

基于定子磁链坐标系的表面式永磁同步电机(surface PMSM,SPMSM)定子磁链幅值和转矩预测模型分别如式(1)和式(2)所示[28-29].

ψs(k+1)和Te(k+1)为下一时刻定子磁链幅值和转矩,ψs(k),Te(k)和δ(k)为当前时刻定子磁链幅值、转矩和转矩角,Vs(k)和α为施加电压矢量的幅值及施加电压矢量与定子磁链的夹角,p为电机极对数,ψf为永磁体磁链,Ld为电机d轴电感,∆t为系统采样周期.

三相两电平电压源逆变器共有8种开关状态,对应8个电压矢量V0-V7,如式(4)所示,其中Vs为施加电压矢量.电压矢量的V0-V7开关状态分别为000,100,110,010,011,001,101和111.

传统模型预测转矩控制下,考虑开关次数控制的成本函数如式(5)所示,其中:λsw为权重系数,nsw为施加电压矢量引起的开关变换次数.

通过设计和调整开关次数权重系数,可调整各控制目标之间的相对重要程度.由式(5)可知,λsw为连续变化量,设计和调整均较为复杂.表面式永磁同步电机传统模型预测转矩控制系统如图1所示.

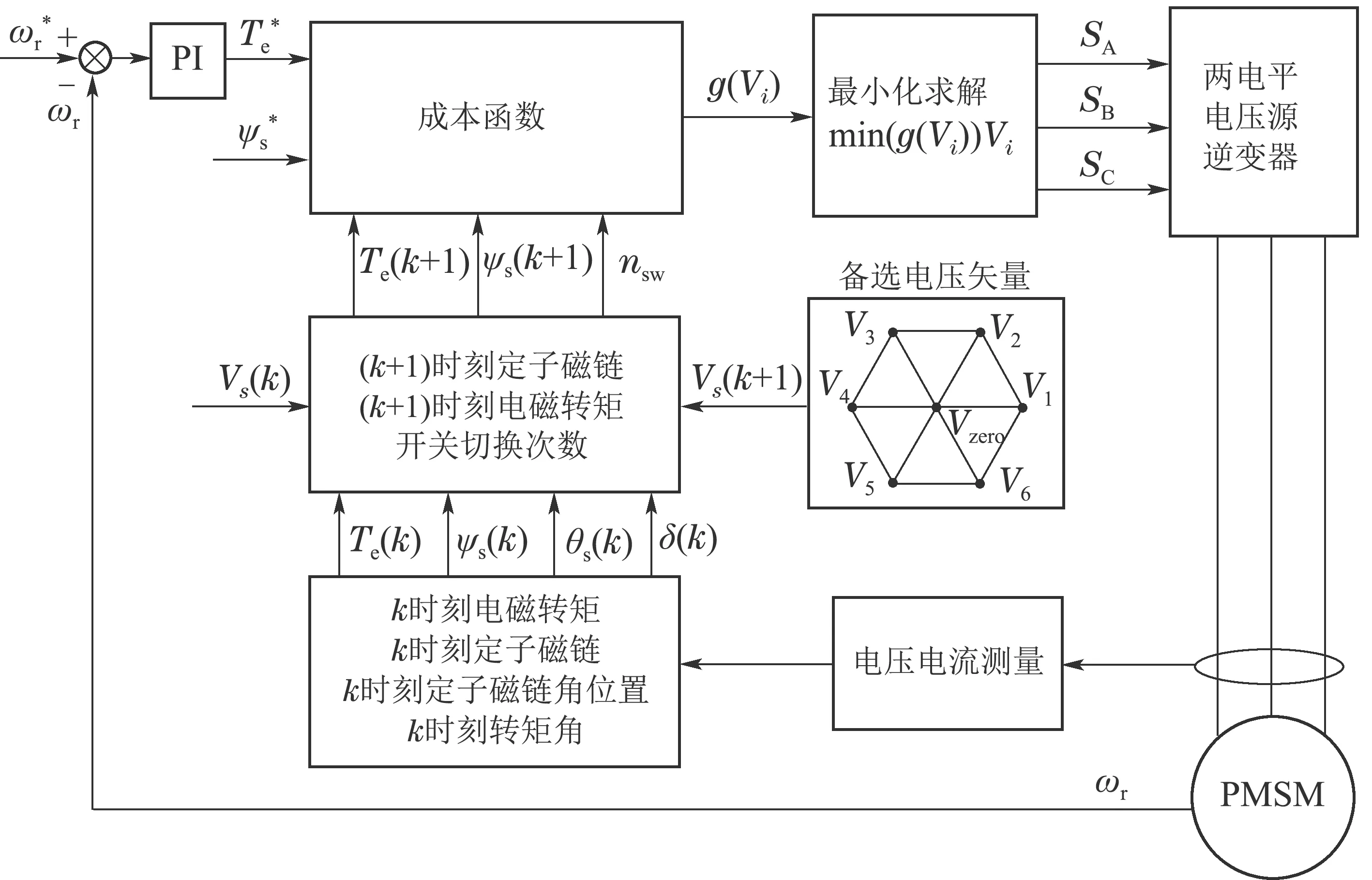
图1 表面式永磁同步电机传统模型预测转矩控制系统Fig.1 Conventional SPMSM MPTC system

3 基于排序法的模型预测转矩控制

为解决成本函数中权重系数设计繁琐的问题,应用排序法的思想,对各个控制目标的预测结果分别评价和排序,从而将不同控制目标的控制效果转换为无量纲且值域统一的排序结果.

基于排序法的成本函数如式(6)所示,其中:r为总排序结果,rflux_torque为转矩与磁链控制成本函数gflux_torque排序结果,rsw为开关次数成本函数gsw排序结果.gflux_torque如式(7)所示,gsw如式(8)所示.

根据当前电压矢量,下一时刻施加的电压矢量引起的开关变换次数是确定的,如表1所示,其中Vzero为施加的零电压矢量.由于V0或V7对磁链和转矩控制效果相同,以开关次数最小为原则选择零电压矢量,可使得基于排序法的模型预测控制只需遍历7个电压矢量[15].

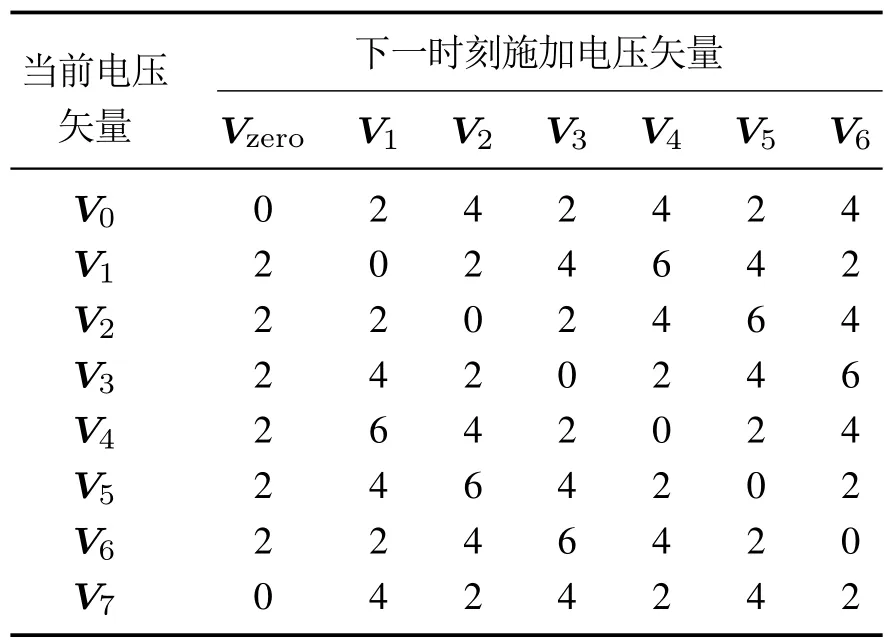
表1 开关切换次数Table 1 Switching numbers

排序法的规则如下: 成本函数最小者记分为0,从小到大依次加1,最大为6.如果两个电压矢量的成本函数相同,则得分相同.因此,所有的控制目标的排序得分值域也相同,均为[0,6].将所有的控制目标的排序得分求和,最终输出总得分最小值所对应的电压矢量.

基于排序法规则和表1所示的开关切换次数表,可建立开关次数排序得分表,如表2所示,从而可以根据当前电压矢量,直接查表得出下一时刻7个电压矢量的开关次数排序得分.

表2 开关切换次数排序得分Table 2 Rankings of switching numbers

由上文可知,排序法将各控制目标的控制效果通过排序进行统一量化映射到[0,6]内的整数,从而消除了不同控制目标之间的量纲差异.但由于排序法得到的排序结果是离散的整数,则存在总排序结果最小值对应的电压矢量不唯一的情况,如表3所示.此时电压矢量V1磁链和转矩控制效果排序为1,开关次数排序为0,总排序结果为1,电压矢量V6磁链和转矩控制效果排序为0,开关次数排序为1,总排序结果也为1.由表3可知,此时排序总结果最小值为1,则对应的最优电压矢量有两个,并不唯一,需要设计优先级以确定最终输出电压矢量.

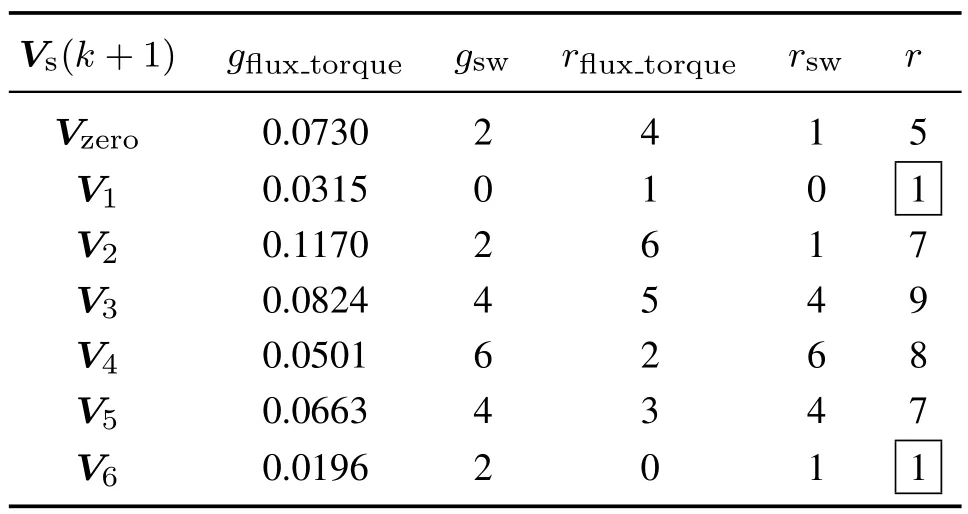
表3 排序法计算示例Table 3 Calculation example of the ranking approach

为解决在排序过程中最优电压矢量不唯一问题,需在排序结束后进行判断总排序结果最小值所对应电压矢量是否唯一.如果电压矢量唯一,则输出该电压矢量,如果电压矢量不唯一,则需设计优先级来唯一确定控制最优解.以上文为例,以转矩与磁链控制优先,则选择rflux_torque结果中的最小值,得到唯一解V6.也可采用开关次数控制优先,选择rsw结果的最小值,得到唯一解V1.考虑优先级筛选的排序法模型预测转矩控制策略流程图如图2所示.

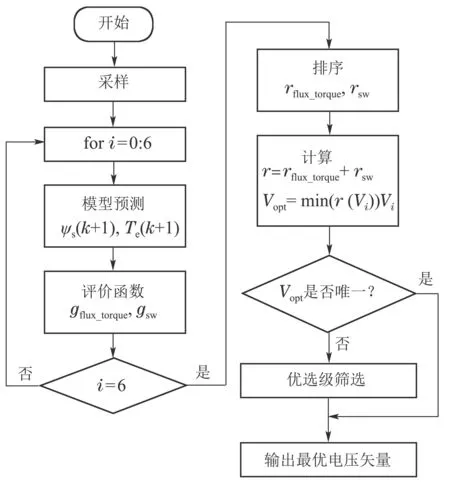
图2 考虑优先级筛选的排序法模型预测转矩控制流程图Fig.2 Flow chart of the MPTC based on ranking approach

基于MATLAB/Simulink建立了表面式永磁同步电机排序法模型预测转矩控制仿真模型,仿真模型为离散模型,采样周期为5×10-5s;直流母线电压为312 V;转速PI(Proportional Integral)调节器参数为KP=5,KI=100,PI调节器输出上下限为[-30 N·m,30 N·m].仿真用表面式永磁同步电机参数如表4 所示.

表4 仿真用表面式永磁同步电机参数Table 4 Parameters of SPMSM for simulation

电机参考转速为400 r·min-1,参考定子磁链幅值为0.3 Wb,仿真时长为1 s,电机负载转矩Tm设定为20 N·m,优先级分别设定为转矩与定子磁链幅值控制优先与开关次数控制优先.电磁转矩和定子磁链幅值仿真波形如图3-4所示.

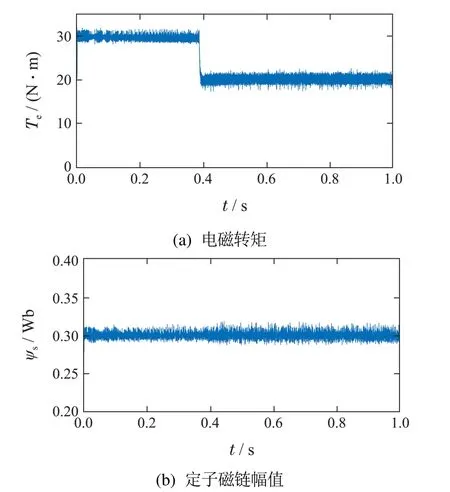
图3 转矩与定子磁链幅值优先控制仿真波形Fig.3 Simulation waveforms using torque and stator flux priority control

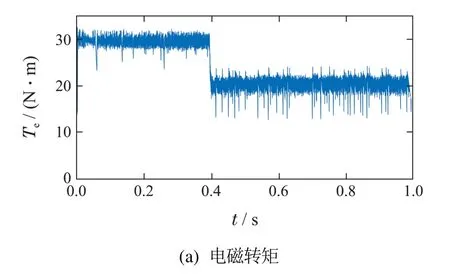
图4 开关次数优先控制仿真波形Fig.4 Simulation waveforms using switching number priority control

定义转矩脉动均方根误差(root mean squared error,RMSE)、磁链脉动RMSE、评价函数平均值和平均开关频率分别如式(9)-(12)所示,其中:n为采样总个数,Nswitching为逆变器开关总次数,t为采样总时长.

不同负载转矩和不同优先级控制下电机系统性能如表5所示.

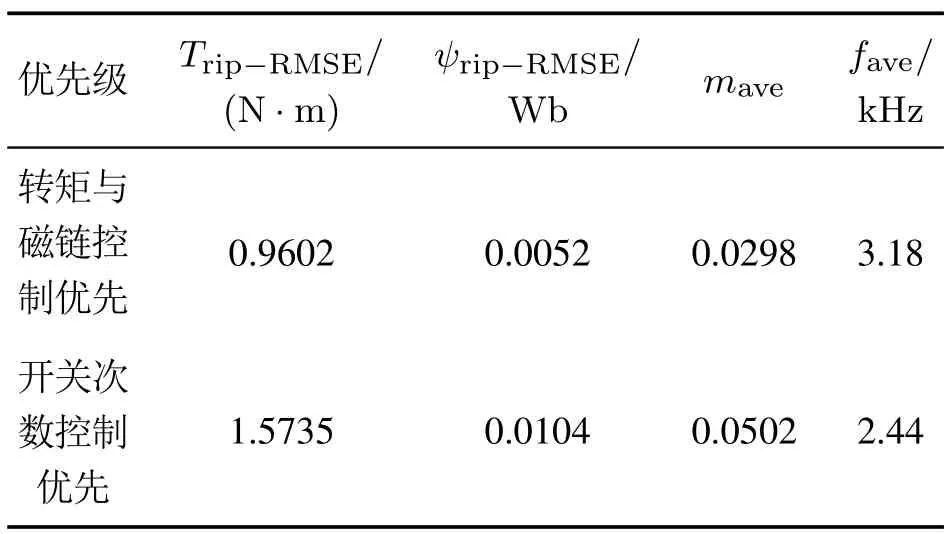
表5 不同优先级控制下电机系统性能Table 5 Performances of motor system under different priority control

仿真结果表明,基于排序法的永磁同步电机模型预测转矩控制可行,并且排序算法中最优电压矢量不唯一的情况确实存在.不同的优先级设计对控制效果有较大的影响,优先的控制目标其性能会更好,但也会影响其余控制目标的控制效果.因此,当转矩与定子磁链幅值控制优先时,则转矩与定子磁链控制性能较好,但平均开关频率较大;当开关次数控制优先时,则平均开关频率较低,但转矩与磁链脉动显著增大.

对于电机控制系统,如果控制目标为转矩控制和磁链控制,一般以转矩控制优先.如果控制目标为转矩与磁链控制综合性能和开关次数,则一般应以转矩与磁链控制优先.

4 排序缩放因子

由上文可知,排序法对各个控制目标的预测结果独立评价和排序,从而将不同控制目标的控制效果转换为无量纲且值域统一的排序结果,从而无需设计权重系数.本质上,排序法将不同控制目标重要性始终均视为相同.但电机系统实际运行中,不同控制目标的重要性并不相同,且随着系统状态实时变化.为使系统控制性能达到最优,成本函数应能够体现各控制目标重要性的差别和时变,随着系统实际状态,实时合理调整各控制目标的相对重要性.因此,传统排序法虽然省去权重系数,但也无法实现对控制目标重要性的调节.为了实现控制目标重要性的调节,在传统排序法的基础上,引入缩放因子k,通过缩放因子k可调节各控制目标排序结果大小,从而赋予不同控制目标不同的重要性.带有缩放因子排序法的成本函数如式(13)所示,其中k为缩放因子,k≥0.

由式(13)可知,缩放因子的效果类似传统模型预测转矩控制的权重系数,可对开关次数控制的重要性进行调节,从而改变系统控制性能.但与连续变化的权重系数不同,由排序规则可知rflux_torque与rsw的值域均为[0,6]内离散的整数,缩放因子k的取值对控制效果的影响也具有有限离散分段的特性.因此,相较于传统权重系数,缩放因子的设计与调整要更为简单.

定义分段点为缩放因子k的临界点,记为k∗.在临界点处,存在两个电压矢量Va和Vb的总排序结果相同,如式(14)所示.

求解式(14),则可得临界点k∗的表达式如下:

将式(16)和式(17)的所有可能取值代入至式(15)则可得到所有可能的临界点,共计23个临界点,如表6所示.由表6可知,改变电压矢量排序结果的临界点只有23个.因此,不同于无限连续的权重系数,排序法使用的缩放因子是有限离散的,从而简化设计与调整的难度.

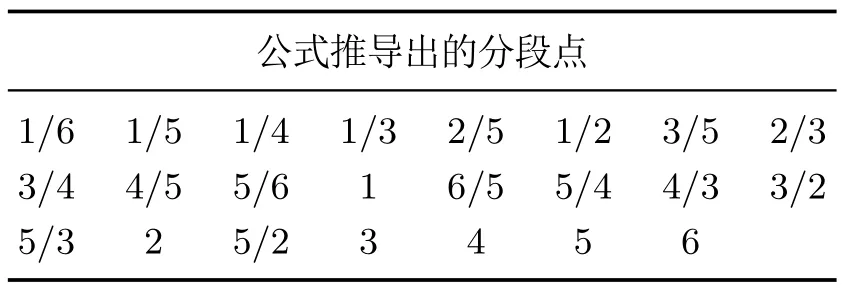
表6 公式推导出的分段点Table 6 Piecewise points derived by formula

仿真结果表明,当缩放因子k>2时,过分减弱对转矩和磁链的控制,导致系统失控.因此,k的取值范围为[0,2].此时,临界点k∗共有18个.

表6中给出的临界点使得总排序结果发生改变的k值.对于模型预测转矩控制仅输出排序结果最小的电压矢量,即如果缩放因子虽然改变排序结果,但没有改变排序结果最小的电压矢量,缩放因子并不改变系统控制性能.因此,实际可影响系统控制性能的临界点仅为所有临界点的一个子集.

表7 不同缩放因子求解电压矢量差异统计Table 7 Difference statistics of voltage vector solved by different scaling factors

由表7可知,k取值于(1/2,3/5)与(3/5,2/3)对输出电压矢量改变的效果相同.因此,实际有效临界点k∗只有10个,如式(18)所示.

因此,可将[0,2]划分成[0,1/6),(1/6,1/5),···,(1,2)这10个区间,k在区间内任意取值,控制效果均相同.当k取值为临界点时,需要优先级判断.当磁链和转矩控制优先时,实际相当于临界点左侧区间,当开关次数优先时,实际相当于临界点右侧区间.以k=2为例,当磁链和转矩控制优先时,实际相当于(1,2),当开关次数控制优先时,实际相当于k>2,此时系统失控.因此,缩放因子的取值范围仅为10个离散区间,缩放因子在区间内任意取值的效果均相同,从而减轻缩放因子的设计和调整难度.

在与上文相同的仿真条件下,缩放因子k在不同区间内取值,电机系统的转矩脉动RMSE、磁链脉动RMSE、评价函数平均值和平均开关频率如表8和图5-8所示.

表8 不同缩放因子控制下的电机系统性能Table 8 Performances of motor system under different scaling factors

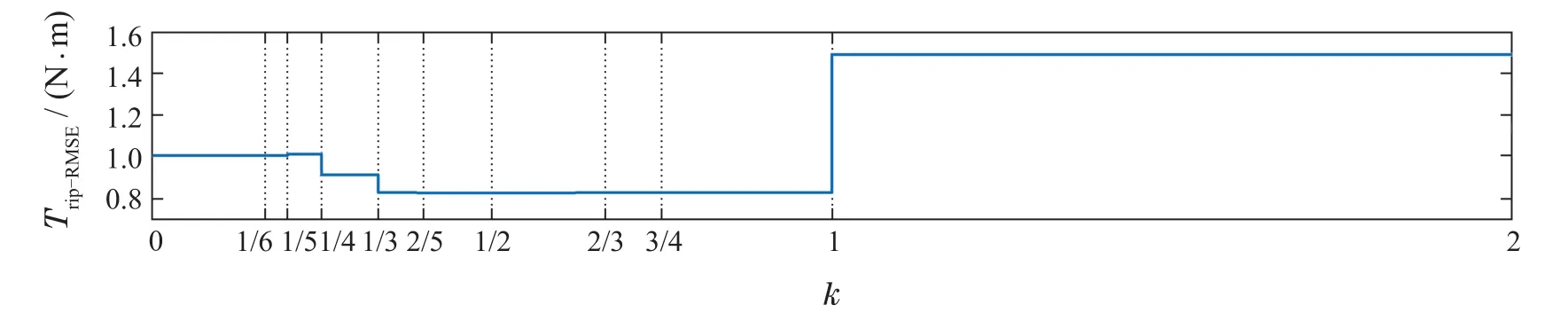
图5 不同缩放因子下的转矩脉动均方根误差Fig.5 RMSE of torque ripple under different scaling factors

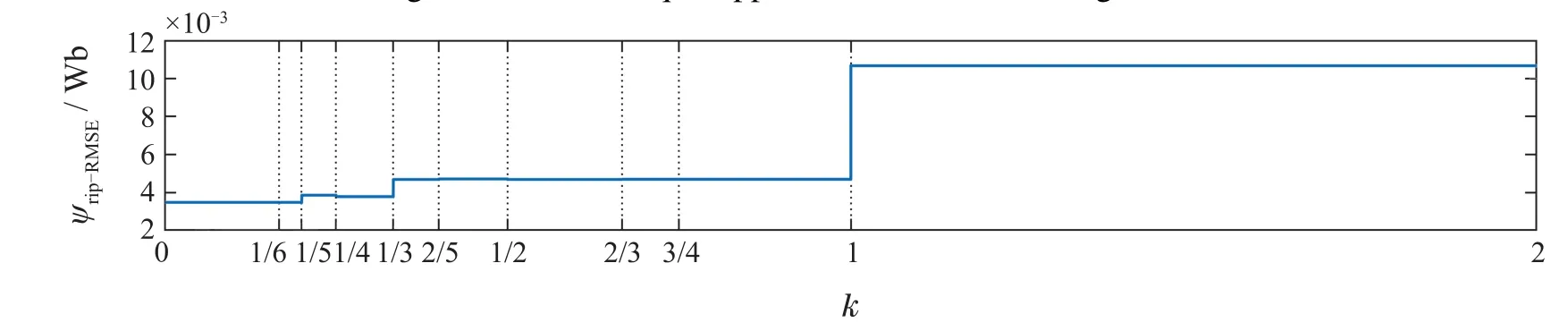
图6 不同缩放因子下的磁链脉动均方根误差Fig.6 RMSE of stator flux ripple under different scaling factors

由仿真结果可知:

1) 随着k的变化,控制效果呈现离散化分段的特点,表明缩放因子取值区间是离散有限的.相较于连续变化的传统权重系数,缩放因子仅有10个离散点,从而简化设计和调整复杂程度.

2) 缩放因子k取值于(3/4,1)区间内的控制效果等同于缩放因子k=1且转矩与磁链控制优先,缩放因子k取值于(1,2)区间内的控制效果等同于缩放因子k=1且开关次数控制优先,验证上文理论分析.

3) 由表8可知,相较于(0,1/6),k取值于(1/6,1/5)改变输出电压矢量的排序情况仅有720 种,占比1.79%;相较于(2/3,3/4),k取值于(3/4,4/5)改变输出电压矢量的排序情况仅有216种,占比0.54%.由于在上文仿真条件下并未出现以上排序情况,表8中k取值于(0,1/6)和取值于(1/6,1/5)及k取值于(2/3,3/4)和取值于(3/4,4/5)的仿真结果完全相同.

4) 由图7-10可知,可将缩放因子取值区间进一步简化划分为[0,1/4),(1/4,1)和(1,2)3段.在每个分段区间内,系统的控制性能基本相当,使得缩放因子的设计和调整更加简单.

图7 不同缩放因子下的评价函数平均值Fig.7 Average evaluation function under different scaling factors

图8 不同缩放因子下的平均开关频率Fig.8 Average switching frequency under different scaling factors

5) 由图7-10可知,随着缩放因子k的增大,平均开关频率减小,磁链脉动RMSE增大,转矩脉动RMSE在(1/4,1)段最小,在(1,2)段最大.

5 基于模糊排序法的模型预测转矩控制

实际运行中,电机系统状态是动态变化的,控制目标的相对重要性也应动态调整.因此,排序法体现控制目标重要性的缩放因子也应动态调整.下文提出基于模糊控制动态缩放因子排序法的模型预测转矩控制策略.模糊控制器使用电机转矩误差绝对值和磁链误差绝对值作为输入变量,缩放因子k作为输出变量.

转矩误差绝对值论域为[0 N·m,2 N·m],分为3个模糊子集{Ts,Tm,Tb},隶属度函数如图9所示.磁链误差绝对值论域为[0 Wb,0.02 Wb],分为3个模糊子集{Ps,Pm,Pb},隶属度函数如图10所示.根据缩放因子的分段特性,模糊控制器输出k值仅在[0,1/4),(1/4,1)和(1,2)这3个区间内选取即可,应避开临界点k∗,避免最优解不唯一现象,省去优先级判断,简化控制算法.因此,缩放因子k的论域为[0,2],分为3个模糊子集{ks,km,kb},隶属度函数如图11所示.

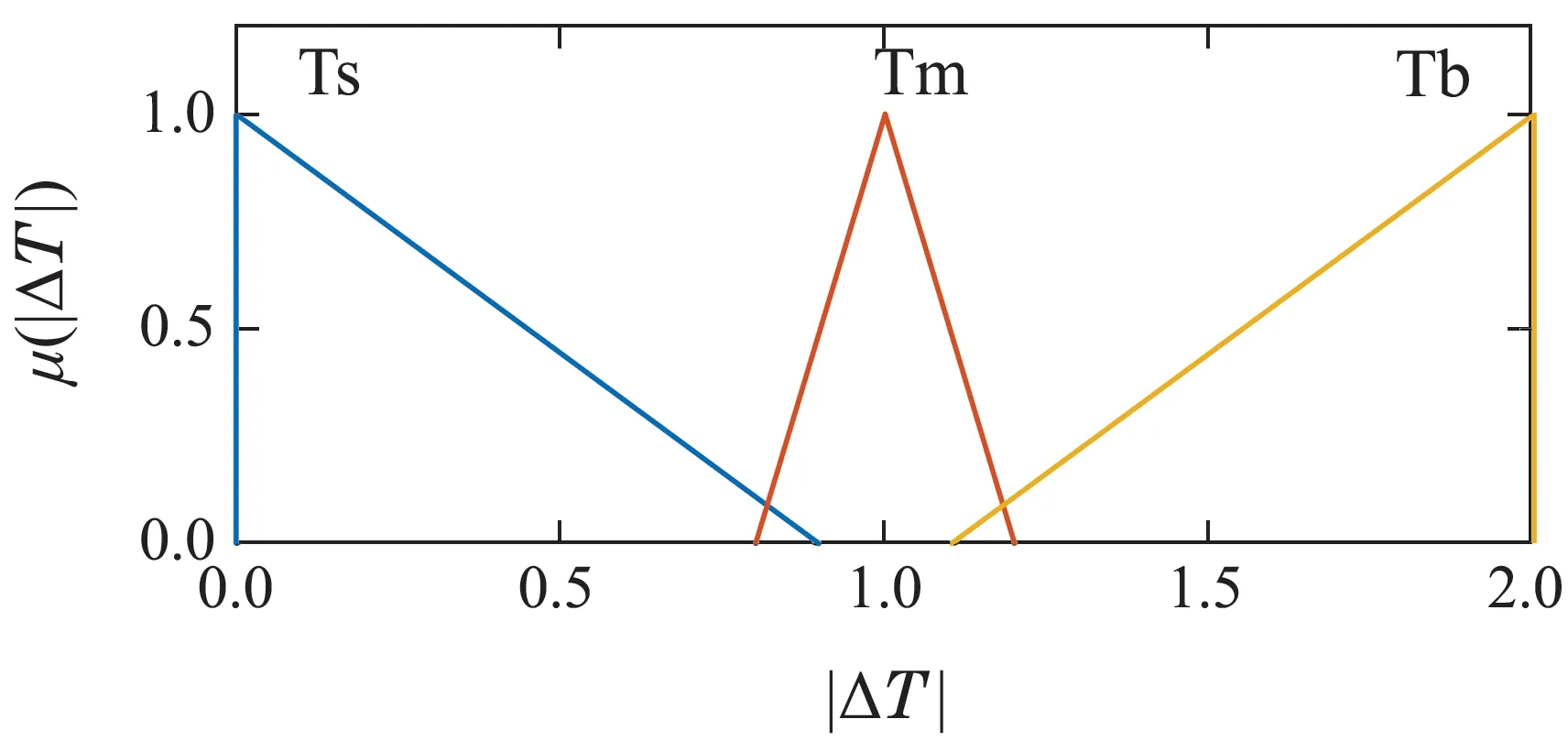
图9 转矩误差绝对值隶属度函数Fig.9 Membership function of torque error

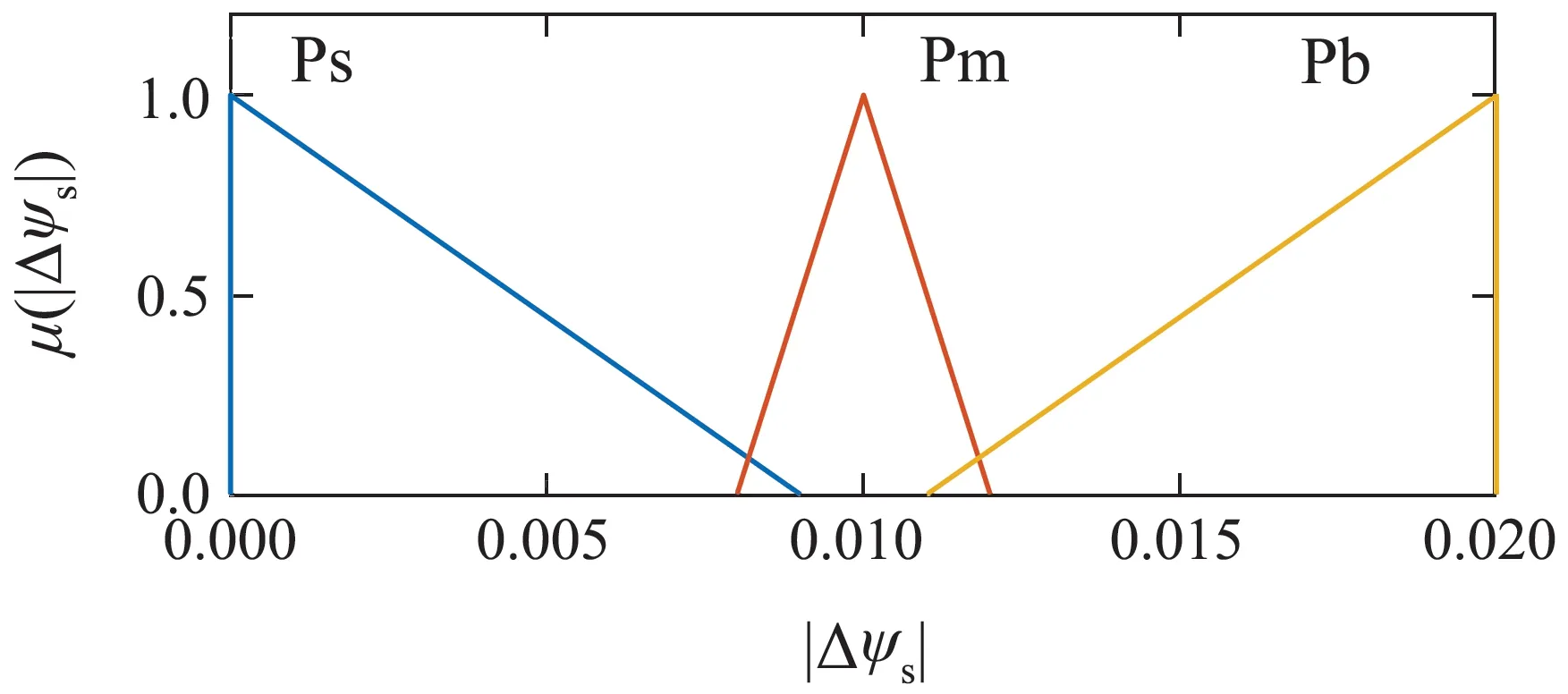
图10 定子磁链幅值误差绝对值隶属度函数Fig.10 Membership function of stator flux error

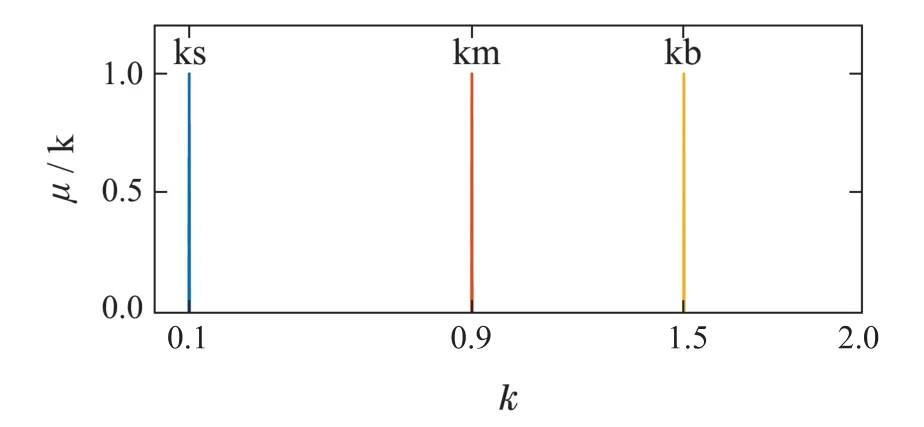
图11 缩放因子隶属度函数Fig.11 Membership function of scaling factor

由上文可知: 随着缩放因子k的增大,平均开关频率减小,磁链脉动RMSE增大,转矩脉动RMSE在(1/4,1)段最小,在(1,2)段最大.因此,当磁链脉动过大时,将缩放因子调整至[0,1/4)内,以降低磁链脉动;当转矩脉动过大时,将缩放因子调整至(1/4,1)内,以降低转矩脉动;当转矩脉动和磁链脉动均得到较好的控制时,可将缩放因子调整至(1,2)内,以降低系统开关频率.

根据上述规律,建立模糊控制规则表,如表9所示.模糊推理采用Mamdani型推理,解模糊采用max-min法,取最大隶属度对应输出为缩放因子k.

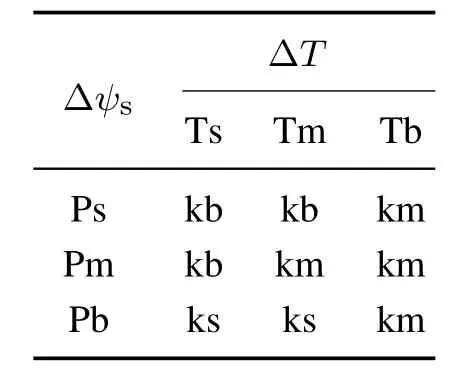
表9 模糊控制规则Table 9 Fuzzy control rules

基于模糊排序法的永磁同步电机模型预测转矩控制系统如图12所示.

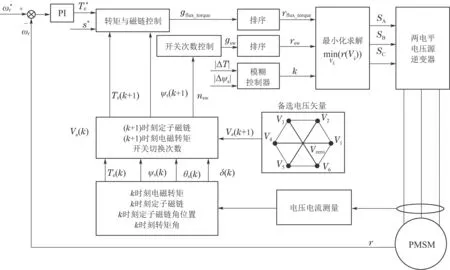
图12 基于模糊排序法的永磁同步电机模型预测转矩控制Fig.12 The PMSM MPTC system based on fuzzy ranking approach

6 仿真验证

建立基于模糊控制排序法的永磁同步电机模型预测转矩控制系统仿真模型,验证控制策略的控制性能,并与传统固定权重系数和模糊权重系数的模型预测转矩控制进行比较,其中传统固定权重系数通过试验搜索法确定[10],模糊权重系数控制器设计如文献[15]所示.仿真验证条件如下: 电机由静止状态启动至转速为400 r·min-1,2s 时转速阶跃至-400 r·min-1.负载转矩初始为20 N·m,1 s时阶跃至-20 N·m,3 s时阶跃至20 N·m,仿真总时长为4 s.

图13-15所示分别为采用传统固定权重系数、模糊权重系数和基于模糊排序法的模型预测转矩控制下的转速、电机转矩和定子磁链幅值.不同控制策略下,电机系统性能如表10所示.

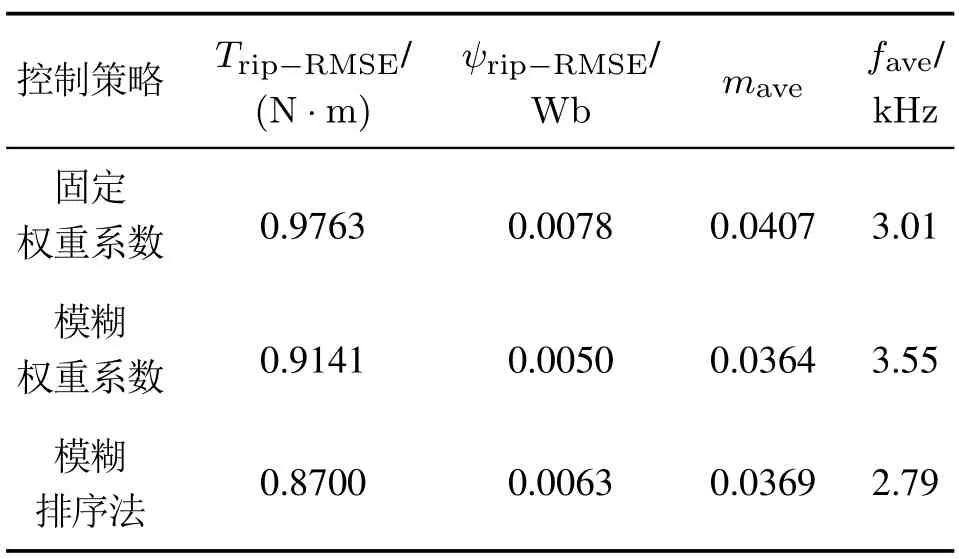
表10 不同控制策略下电机系统性能Table 10 Performances of motor system under different control strategies

图13 采用固定权重系数的仿真波形Fig.13 Simulation waveforms using the fixed weighting factor control

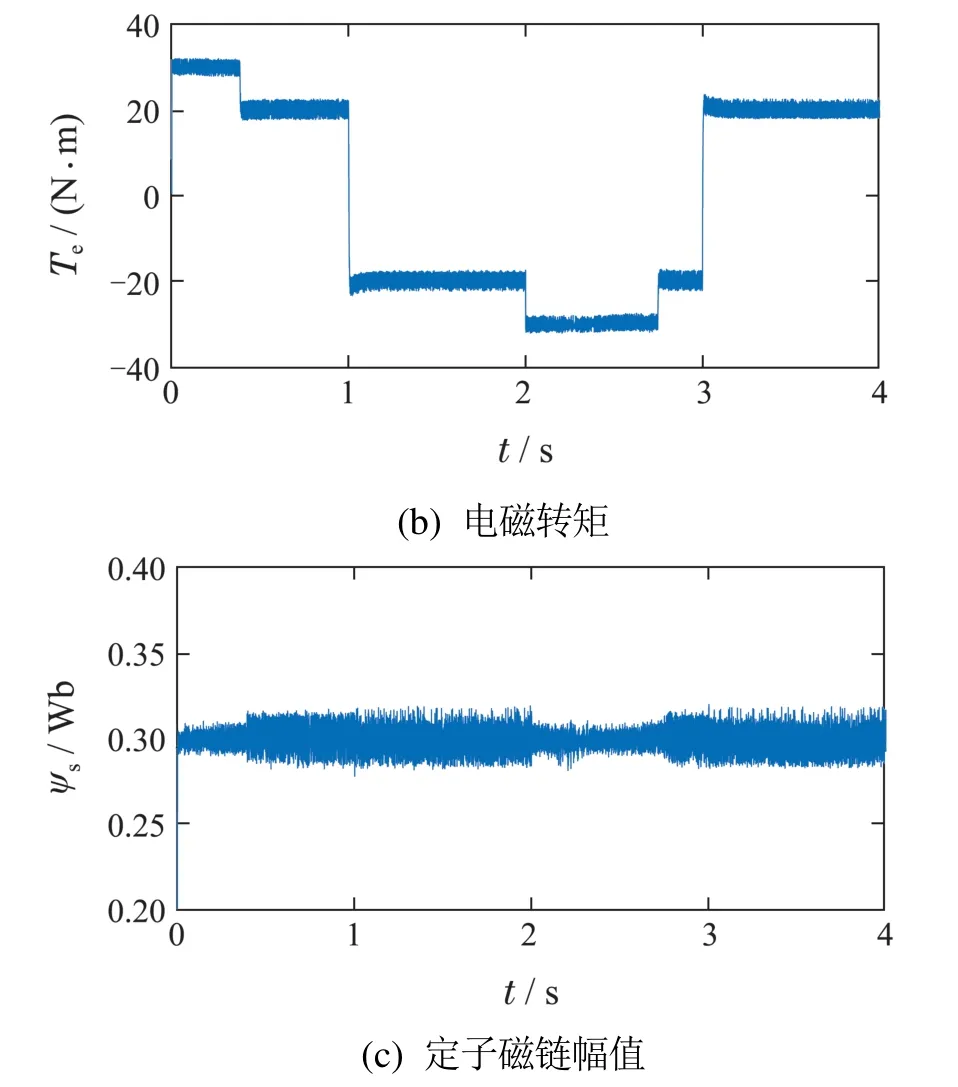
图14 采用模糊权重系数的仿真波形Fig.14 Simulation waveforms using the fuzzy weighting factor control

图15 采用模糊排序法的仿真波形Fig.15 Simulation waveforms using the fuzzy ranking approach control

由仿真结果可知:

1) 基于模糊排序法的永磁同步电机模型预测转矩控制系统运行良好,可实现电机四象限运行.

2) 与固定权重系数的传统模型预测转矩控制相比,模糊排序法控制下平均开关频率更低,转矩与磁链脉动更小,综合控制性能更优越,且可有效抑制动态下的磁链和转矩脉动.但由于模糊排序法动态调节控制目标重要性,兼顾转矩、磁链和开关次数控制,当动态加载时,会牺牲转矩控制性能,导致转速恢复的动态响应要变慢.与模糊控制调节权重系数的模型预测转矩控制相比,模糊排序法控制下平均开关频率更低,转矩脉动有所减小,但磁链脉动略有上升,综合控制性能基本相当.

3) 传统模型预测转矩控制权重系数固定,并不适于实时变化的运行工况.由于权重系数连续变化且变化范围较大,模糊控制调节权重系数的模糊规则设计较为复杂.模糊排序法根据系统状态动态调节缩放因子,在工况变化下电机系统也能有良好的控制性能.由于缩放因子调节区间离散有限,模糊规则设计简单易行.

7 排序法实时性分析

排序法虽然采用无量纲的排序得分解决权重系数设计问题,但也带来额外的排序计算.当备选电压矢量数目较多及控制目标数量较多时,一定程度上会影响模型预测控制的实时性.

传统模型预测转矩控制算法分为预测和寻优两个过程.排序法模型预测转矩控制需要在预测过程之后对预测结果计算排序得分求和,基于排序总得分进行寻优,可分为预测、排序和寻优3个过程.

对于预测过程,传统模型预测转矩控制与排序法模型预测转矩控制均需计算下一时刻的磁链与转矩变化量、开关次数变化量,两者计算量相同.

对于排序过程,传统模型预测控制无需排序,排序法模型预测控制需要进行不同控制目标的成本函数排序得分计算和排序得分求和.这里需要指出,排序法仅关注排序得分,而无需实现排序.因此,下文采用比较赋值排序法计算排序结果得分.具体实现如下: 令各电压矢量初始得分均为0,将电压矢量V0的预测结果分别与之后的6个电压矢量进行比较,每次比较中预测结果较大的电压矢量得分加1,其次将电压矢量V1的预测结果分别与之后的5个电压矢量进行比较.经过6轮的比较,则可得到全部电压矢量的排序得分,如图16所示.与传统冒泡法相比,由于不改变电压矢量位置,无需数据交换,便于多控制目标排序得分求和计算.

图16 比较赋值排序法Fig.16 Ranking approach

以7个备选电压矢量,2个控制目标为例,比较赋值排序法则需要额外进行[2×(6+5+4+3+2+1)]=42次数据比较.因此,如果备选电压矢量数目为m,控制目标数量为n,则排序法需要额外进行次数据比较和1次排序得分求和.

对于寻优过程,传统模型预测转矩控制与基于排序法的模型预测转矩控制的寻优过程计算量基本相同,均需进行(m-1)次数据比较.但由于排序求和得分最小结果可能不唯一,排序法模型预测控制需要额外进行最优电压矢量是否唯一的判断.

基于STM32H743单片机对传统模型预测转矩控制与排序法模型预测转矩控制进行单步仿真验证.为评价排序算法的耗时,仅采用查表方式得出开关切换次数,并没有采用查表形式直接给出分数,依然采用比较赋值法计算得出.单步测试电机控制系统参数与上文仿真系统相同.单步测试初始值如下: 定子磁链幅值为0.3077 Wb,定子磁链角位置为114.8818◦,参考转矩值为20.4694 N·m,转矩值为19.0727 N·m,转矩角为30.8784◦,定子磁链参考值为0.3 Wb,上一时刻施加电压矢量为V4.

传统模型预测转矩控制与排序法模型预测控制的单步执行时间如表11所示,其中时间数据为重复运行10000次单步验证时间的平均值,预测过程时间为计算各控制变量的预测值及控制目标对应的成本函数耗时,排序过程时间为采用比较赋值排序法,依据控制变量的预测结果得到各电压矢量的不同控制目标对应的排序得分,并求和的耗时,寻优过程时间为依据求和结果得到最优电压矢量的耗时,总时间为预测过程、排序过程和寻优过程时间的总和.

表11 模型预测转矩控制单步执行时间Table 11 Algorithm execution times of MPTC

由表11可知,传统模型预测转矩控制与排序法模型预测控制的预测过程时间基本相同,但排序法模型预测控制额外增加排序过程时间,并且由于需要额外增加最优电压矢量是否唯一的判断,寻优过程时间比传统模型预测控制略有增大,从而使得排序法模型预测转矩控制的总时间要大于传统模型预测转矩控制.但以排序法模型预测控制为例,预测过程耗时占比90.47%,排序过程占比8.35%,寻优过程占比1.18%.相较于传统模型预测控制,排序法模型预测控制的计算耗时仅增加8.57%.因此,虽然排序法一定程度上增加系统计算负担,但相较于预测过程,排序法额外增加的计算量较小,不会严重降低模型预测转矩控制的实时性.

8 结论

1) 基于排序法的永磁同步电机模型预测转矩控制将磁链和转矩控制及开关次数控制转换为无量纲的排序结果,从而无需设计权重系数,但存在最优电压矢量不唯一的情况,需要设计优先级,并且不同的优先级设计对控制效果有较大的影响.

2) 排序法将不同控制目标相同对待,虽然省去权重系数设计,但与电机实际系统不符合.缩放因子可调节不同控制目标的重要性,且缩放因子的作用效果具有离散分段特性,从而极大减轻缩放因子的设计和调整难度.

3) 基于缩放因子在不同区间内对转矩、磁链和开关频率的控制效果,采用模糊控制动态调整缩放因子,在电机运行工况变化下,系统始终有良好的控制性能.与固定权重系数的传统模型预测转矩控制相比,平均开关频率更低,转矩与磁链脉动更小,且可有效抑制动态下磁链和转矩脉动.

4) 排序法增加了系统计算负担,但相较于预测过程,排序法额外增加的计算量较小,不会严重降低模型预测转矩控制的实时性.