有色量测噪声下带广义未知扰动的递推上限滤波

秦月梅,周倩倩,杨衍波,梁 彦,潘 泉

(1.西安邮电大学自动化学院,陕西 西安 710121;2.西北工业大学 自动化学院,陕西 西安 710129)

1 引言

离散时间动态系统状态估计问题广泛存在于自动控制[1]、导航制导[2]、目标跟踪[3-5]等军、民用领域[6].针对仅受高斯白噪声扰动的线性系统,卡尔曼滤波给出了最小线性均方误差下的最优估计.然而在诸如非合作目标跟踪的典型应用场景[7-8],高斯白噪声的假设很难成立.例如,由于持续干扰或快速采样等,导致量测值受有色噪声[9-10]的影响.又如,博弈对抗环境下,量测的先验标称模型与实际模型往往失配,使获得的量测数据表征为先验标称模型上施加了缺少先验信息的未知扰动.

一般地,针对有色噪声处理方法有自适应滤波法[11]、状态增广法[12-13]和量测差分法[14].常见的自适应滤波算法[11],利用历史残差序列来估计有色噪声的协方差矩阵实现对有色噪声的拟合和修正,但是增大了滤波算法内存和计算量.状态增广法[13]将有色噪声扩维生成新的状态方程,一方面增加了计算负担;另一方面,重构的系统系数矩阵在滤波过程中可能带来数值不稳定.量测差分法通过相邻历元的观测值线性组合构造出只含有高斯白噪声和一步延迟状态的伪量测模型,有效避免上述两种算法带来的数值问题和病态计算.针对含有色量测噪声的线性系统,文献[14]对量测差分后的伪量测模型进行3 种等效性研究分析,提出了一种更易实现、更易推广到非线性系统的差分法.

实际工业过程中,受目标伪装、欺骗,以及复杂地球磁场干扰影响,量测值获取过程中受有色噪声和未知扰动共存影响.上述算法不具备抵制观测异常和动力学扰动异常影响[15-16].实际非合作目标跟踪过程中,复杂外部环境和系统偏差不仅需要考虑有色噪声,还需要进一步考虑广义未知扰动(generalized unknown disturbance,GUD)的存在.这类扰动无任何先验信息故无法利用噪声进行有效建模.针对特性未知GUD的自适应滤波器[17-19]将系统辨识与滤波有机地结合为一体,对未知参数进行辨识和修正.近年来,针对含GUD的线性系统,文献[4-5,19]通过构造上限滤波器,自适应地最小化状态预测误差、新息协方差和估计误差协方差矩阵上界,有效抑制滤波误差的峰值.

现有针对有色噪声和广义未知扰动下的滤波算法研究,不是将复杂干扰建模为协方差未知的零均值随机噪声就是假设GUD 有确定的系统模型.例如,文献[13]将未知扰动建模为协方差未知的不确定噪声,通过确定噪声协方差的扰动域计算未知参数,提出了一种混合不确定系统鲁棒Kalman滤波器.实际上,广义未知扰动具有间断性且无任何先验信息,实际干扰状态模型难以建立.目前,文献[5]所提的最小上限滤波器针对具有统计约束扰动的离散时间线性随机系统,具有较好的滤波效果,可有效解决广义未知扰动,但无法适用于有色量测噪声下带广义未知扰动的随机动态系统.针对该受干扰系统,一方面有色噪声的存在导致相邻时刻间量测相关,不满足扩展上限滤波要求噪声独立的基础,不再适用于已有的上限滤波框架;另一方面,广义未知扰动的存在导致理论的估计误差协方差很难在线计算,无法利用有色量测噪声下类卡尔曼滤波框架获得高精度在线估计.

基于上述讨论,本文基于上限滤波框架提出一种有色噪声下最小上限递推滤波框架.首先,在有色噪声白化框架下,借助多拍优化参数构造新息协方差上限以表征重构的量测方程中多拍广义未知扰动的影响,以在线计算估计误差协方差的上限代替估计误差协方差,提出具有递推结构的有色噪声下上限滤波(upper-bound filter with colored noises,CUBF);其 次,将估计误差协方差上限最小化转化为在线标量参数优化,通过求解线性矩阵不等式获得最优滤波参数以得到有色噪声下最小上限滤波(minimum CUBF,CMUBF).

符号=:表示定义,(·)表示与相邻公式相同的内容.I和O分别为合适维数的单位阵和零矩阵.对于任意两个(半)正定阵A和B,若A-B为正定阵或半正定阵,则可记为A>B或A≥B.Rn代表n维实向量所构成的空间.

2 问题描述

考虑如下离散时间随机线性系统动态方程:

其中:xk∈Rn和zk∈Rm分别为系统状态向量和量测向量;Fk为系统传递矩阵;Hk为观测矩阵;Ak+1为扰动系数矩阵,且各矩阵具有合适的维数;wk∈Rn为高斯白噪声,其协方差矩阵Qk≥0;vk∈Rm为服从下式(2)的有色噪声,即

其中:Mk为噪声系数矩阵;ek为高斯白噪声,且其协方差矩阵Rk>0.wk和ek互不相关.初始状态x0为均值¯x0,协方差P0的高斯随机向量与wk,vk,ek均不相关.

参考文献[3],GUD统计模型如下所示:

本文拟在有色噪声白化框架下,以在线计算估计误差协方差的上限代替理论估计误差协方差,利用线性矩阵不等式求解最优滤波参数,实现有色噪声下最小上限滤波的递推.拟设计的CMUBF具有如下优点:

1) 以估计误差协方差上限代替理论估计误差协方差来刻画未知扰动对滤波的影响,相比于未知扰动在线辨识更容易实现,放宽了滤波器设计条件;

2) 估计误差协方差上限的构造不需要依赖过多参数,相应滤波器的递推实现具有更强的可设计性和灵活性;

3) 用于求解最优滤波参数的线性矩阵不等式依赖当前量测,既保证滤波充分挖掘有效量测信息,又使得滤波器设计对建模误差有一定鲁棒性.

3 有色量测噪声下递推上限滤波

在有色噪声白化框架下,以在线计算状态估计误差协方差的上限代替理论估计误差协方差.通过构造多拍滤波参数并在线优化,实现有色量测噪声下递推上限滤波.

3.1 有色噪声下递推上限滤波框架设计

利用量测差分将有色噪声白化以构建新量测方程,即

其中残差rk+1中含无先验信息的δk+1和δk,因此无法通过在线计算其协方差来对新息协方差进行在线补偿.文献[4-5,19]仅针对量测模型中含有单一时刻扰动的递推上限滤波问题,并未涉及量测模型中含有多拍广义未知扰动的情况.针对此情况,本文引入双滤波参数以构造状态估计误差协方差上限,实现有色量测噪声下上限滤波设计.考虑到双滤波参数求解的复杂性,拟将双滤波参数求解近似为单一参数凸优化,以简化滤波实现过程.

定义1基于式(5)-(8),定义如下满足式(10)-(13)的有色噪声下上限滤波器,即CUBF:

根据上述分析,可得CUBF滤波框架如下所示:

3.2 有色噪声下递推最小上限滤波器实现

理论上,通过引入双滤波参数构造误差协方差上限,进行参数求解时应同时优化滤波参数ϵk和ϵk+1.然而,这个求解过程较为复杂且需要更多的先验信息.故可将k时刻求解获得的“最优”滤波参数作为已知参数直接代入k+1时刻的参数优化求解中,以简化滤波实现过程.如下定理1讨论了有色噪声下递推最小上限滤波的存在性条件.

定理1若满足

定理1的证明过程见附录.

定理1需同时满足式(19)-(20)所示的初值问题及参数优化问题.这里,初始估计误差协方差往往可以设置较大数值作为误差协方差上限.对参数优化而言,通过求解线性矩阵不等式(24)求得满足的滤波参数ϵk+1,进一步地,结合式(23)-(24)解出使得线性矩阵不等式(21)-(22)成立的最优参数及增益,得到CMUBF的递推实现.

将式(18)代入式(24),结合式(23),滤波参数ϵk+1的求解可简化为下述线性矩阵不等式(26),即

注1为简化上述双参数优化下的线性矩阵不等式(26)的求解,在k+1 时刻,将k时刻已求解获得的滤波参数作为已知值代入式(26),将上述双参数优化的线性矩阵不等式求解简化为单参数优化下的线性矩阵不等式求解,以保证其求解的稳定性以及所设计的CMUBF的递推计算实时性.

注2考虑到诸如非合作目标跟踪等对实时性要求较高的实际应用场景,为进一步保证所设计的CMUBF递推求解的实时性,可通过如下特征值求解近似上述线性矩阵不等式(26)的参数优化,即

注3当Mk-1=O2时,所提CMUBF可退化为广义未知扰动下递推上限滤波方法[5];当ϵk+1=0时,所提CMUBF可退化为有色量测噪声下离散时间动态系统滤波方法[14].当Mk-1=O2,ϵk+1=0时,所提CMUBF可退化为传统卡尔曼滤波方法.事实上,所提CMUBF可同时处理有色量测噪声和广义未知扰动,其递推框架具有更加一般的意义.

为方便理解,表1和图1分别给出了所提CMUBF的算法步骤和递推实现框图.

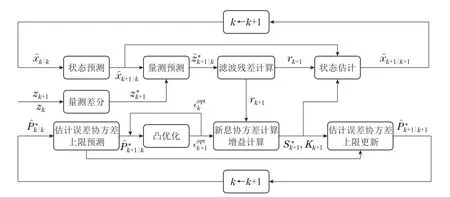
图1 CMUBF递推结构框图Fig.1 The recursive block diagram of CMUBF

表1 CMUBF算法步骤Table 1 The computational procedure of the CMUBF

4 仿真分析

考虑博弈对抗环境下伴随有色量测噪声的非合作目标快速跟踪,目标在o-ξη平面进行匀速直线运动,其初始位置为(100000 150000)Tm、初始速度为(200 150)Tm/s.目标动力学模型如式(1)所示,“⊗”为矩阵Kronecker积运算.Qk=I4.采样步长T=1 s,采样时刻k≤200 s.

该目标被位于坐标原点的高频采样雷达所探测,并获得受有色噪声和未知扰动污染的量测信息.相应量测模型如式(1)所示,且有色量测噪声建模为式(2).Hk=[1 0]⊗I2,Ak+1=I2,Rk=1002×I2,Mk=m×I2,其中“m”为可变的噪声系数矩阵参数,令m=0.7.

当k<50 s 时,GUD 表现为周期为25 s 的梯形波,相应起始值为350 m、峰值为700 m;当50 s ≤k<150 s时,表现为形如600 sin(2πk/50)m的正弦波;当150 s ≤k≤200 s时,GUD 表现为周期为25 s的梯形波,相应起始值为-350 m、峰值为-700 m.

将所提CMUBF与卡尔曼滤波(简记为KF)、有色量测噪声下卡尔曼滤波(简记为CbKF)[14]、广义未知扰动下最小上限滤波(简记为MUBF)[15]进行对比.所有对比算法初始状态估计、初始误差协方差以及未知扰动干扰保持一致,即=(100200 215,150250 170)T,P0=104×diag{5,0.1,5,0.1},且未知扰动干扰如下图2所示.

图2 广义未知扰动示意图Fig.2 The schematic diagram of GUD

图3给出了1000次蒙特卡洛(Monte Carlo)仿真下各方法在ξ方向和η方向的位置和速度估计的均方根误差(root mean square errors,RMSEs)对比.明显地,从图3可以看出,由于既没有考虑有色噪声,又没有考虑GUD,KF算法的RMSEs最大;CbKF和MUBF要么仅考虑有色噪声,要么仅考虑GUD,因此两者RMSEs居中;所提CMUBF同时考虑了有色噪声和GUD,相应的RMSEs在绝大多数时刻明显低于KF,CbKF和MUBF等对比算法的RMSEs.这种现象说明所提CMUBF在这种情况下取得最好的滤波精度,验证了所提CMUBF的有效性.

图3 各对比算法均方根误差Fig.3 RMSEs of compared algorithms

同时,基于1000次Monte Carlo实现,图4给出了对比方法在不同m值(有色噪声的相关性强度不同)下ξ方向和η方向的位置和速度RMSEs对比.在所考虑的有色噪声系数矩阵参数m取值范围内,由于分别考虑了有色噪声或广义未知扰动,CbKF和MUBF的RMSEs均值皆小于KF的RMSEs均值.进一步地,当m较小时,MUBF的RMSEs均值小于Cb-KF的RMSEs均值,表明此时广义未知扰动对滤波性能的影响占主导地位;当m较大时,MUBF的RMSEs均值大于CbKF的RMSEs均值,表明此时有色噪声对滤波性能的影响占主导地位.特别地,由于同时考虑了广义未知扰动和有色噪声,所提CMUBF的RMSEs均值在所考虑的m取值范围内皆小于所有对比算法的RMSEs均值,且其RMSEs均值随m值的增大而基本保持不动.这表明所提CMUBF相比于所对比算法可以有效解决有色量测噪声下带广义未知扰动的随机动态系统滤波问题,且对m的取值具有一定的鲁棒性.

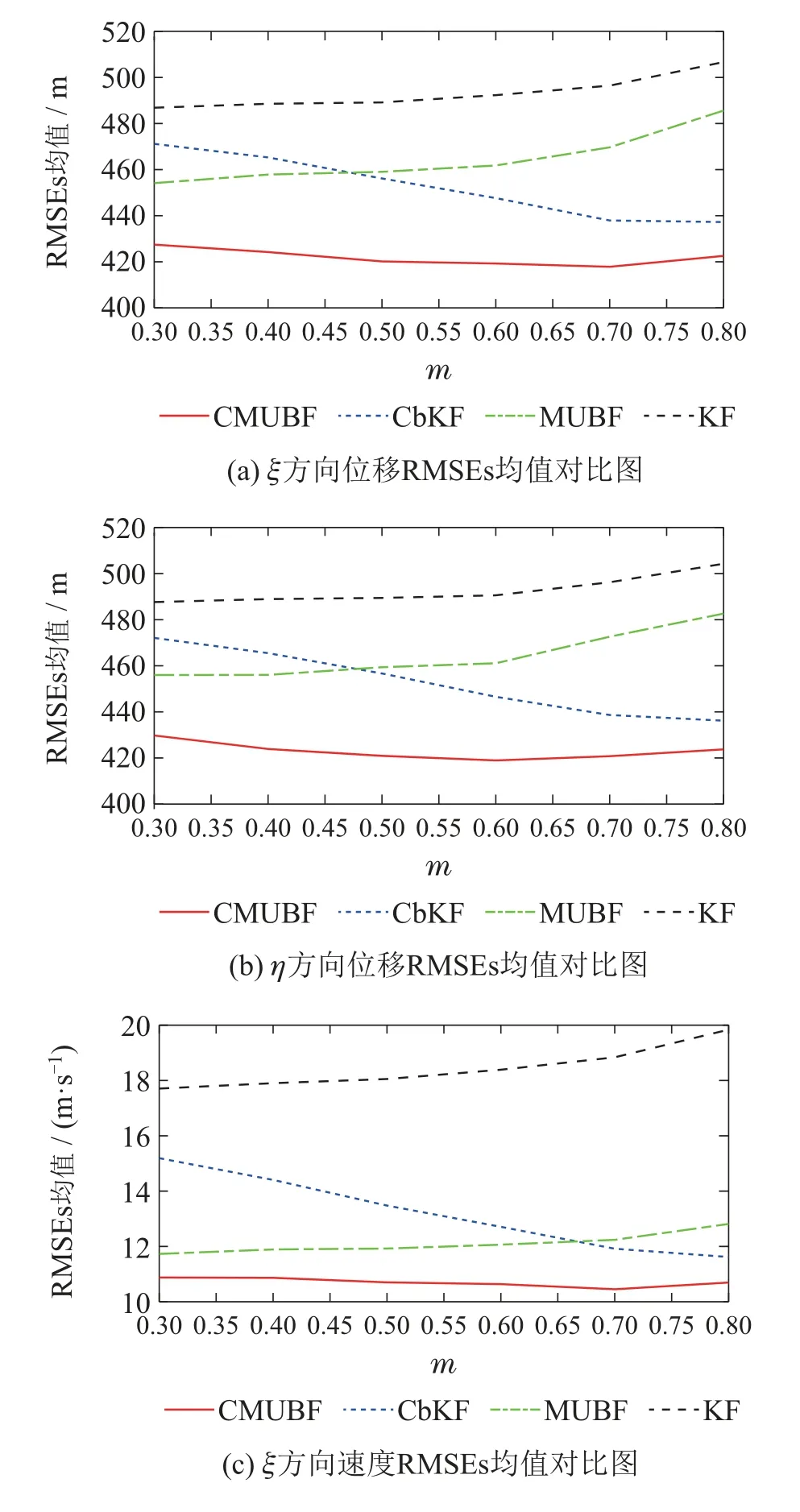
图4 不同m值下各对比算法均方根误差均值Fig.4 Average RMSEs of compared algorithms under different values of m

图5给出了所提CMUBF在不同正定矩阵D(即:D1,D2和D3)下基于1000次Monte Carlo 实现的目标位置估计和速度估计的RMSEs曲线.这里,D1=diag{1,1},D2=diag{100,10},D3=diag{10,100}.不同正定矩阵下所提CMUBF的RMSEs曲线基本一致,表明该算法对于正定矩阵D的取值不敏感.

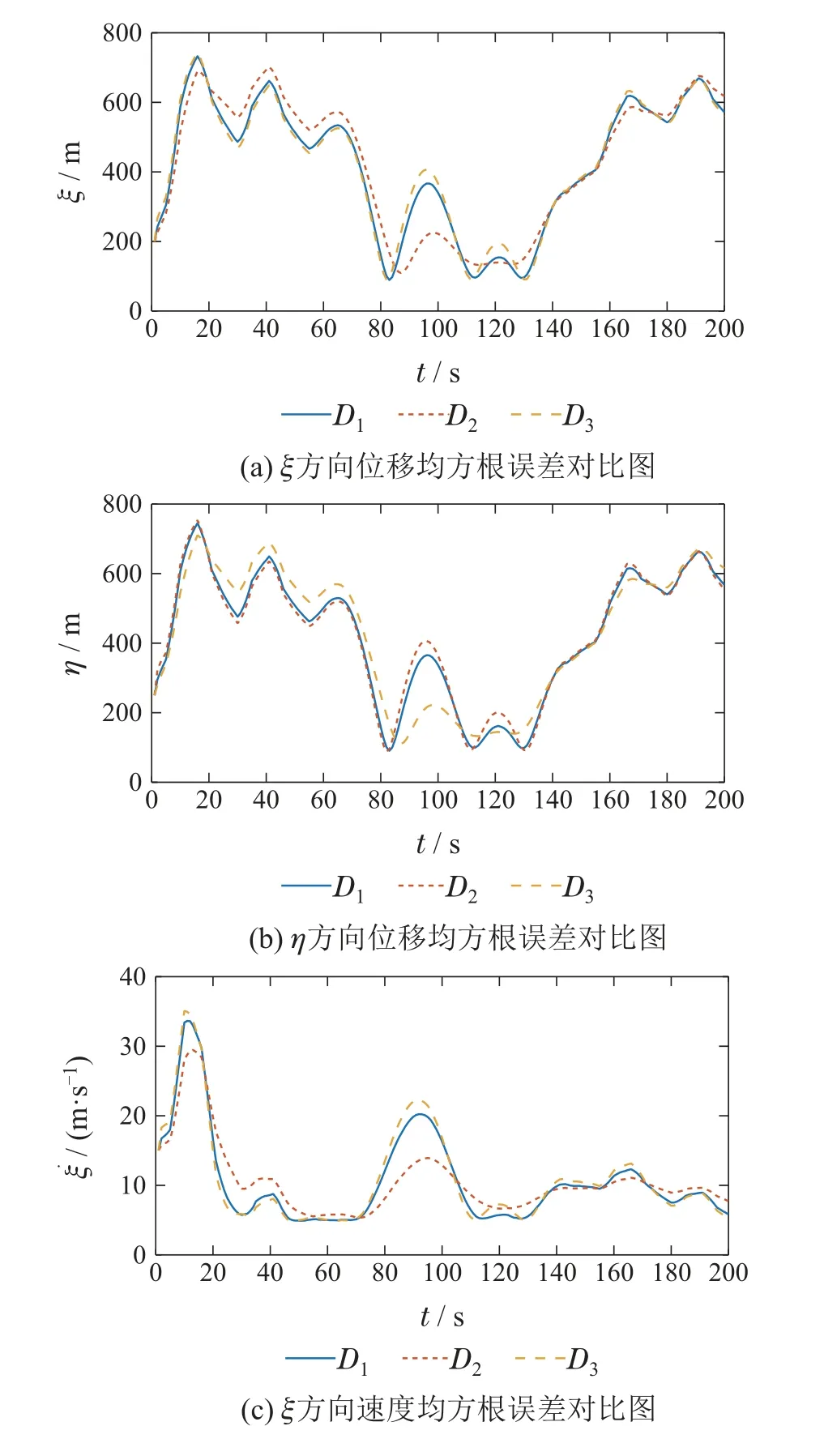
图5 不同D值下CMUBF算法均方根误差Fig.5 RMSEs of CMUBF with different values of D

最后,图6给出了所提CMUBF 在不同初始估计误差协方差矩阵P0(即:P01,P02,P03,P04和P05)下基于1000次Monte Carlo 仿真实现的目标位置估计和速度估计的RMSEs 曲线.P01=103×diag{1,0.02,1,0.02},P02=103× diag{5,0.1,5,0.1},P03=104×diag{5,0.1,5,0.1},P04=105×diag{5,0.1,5,0.1},P05=105×diag{25,0.5,25,0.5}.当系统运行时间较短时,不同初始估计误差协方差P0下所提CMUBF 的RMSEs 波动较大(即P0较大时,速度估计的RMSEs较大;P0较小时,位置估计的RMSEs 较大),这是因为此时初始估计误差协方差矩阵对当前滤波影响较大;当系统运行时间足够长时,不同初始估计误差协方差P0下所提CMUBF 的RMSEs 曲线基本一致,此时,初始估计误差协方差阵对当前滤波的影响几乎可以忽略.该现象表明,在系统短时运行时,所提滤波方法的有效执行依赖初始估计误差协方差矩阵的设定,此时,为获得高精度估计结果,应取较为准确的初始估计误差协方差矩阵(比理论值适当偏大以满足式(19),即≥P0|0);当系统长时间运行时,所提滤波方法的估计精度不依赖于初始估计误差协方差矩阵.因此,从滤波精度角度而言,为获得较高精度的估计结果,在条件允许的前提下,建议初始估计误差协方差矩阵的取值略大于理论初始估计误差协方差矩阵.

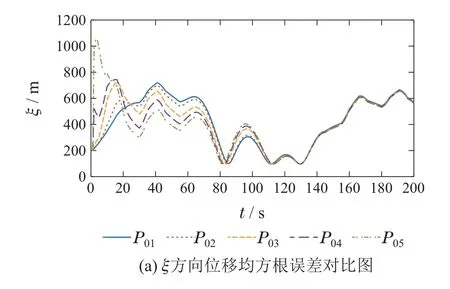
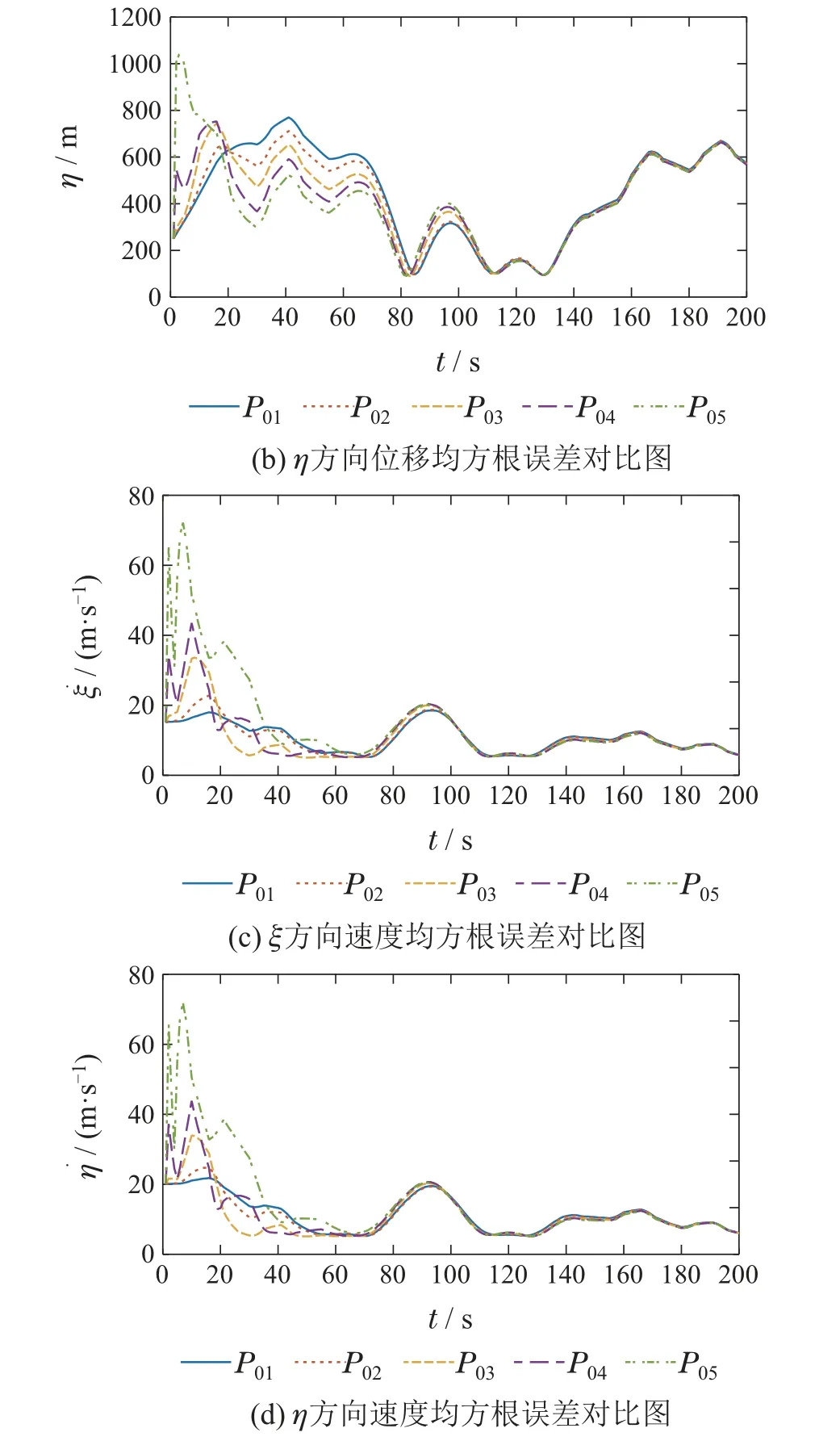
图6 不同P0值下CMUBF算法均方根误差Fig.6 RMSEs of CMUBF with different values of P0

5 结论

针对有色量测噪声下带广义未知扰动的随机动态系统,本文提出了有色噪声下递推最小上限滤波.利用量测差分对有色噪声白化处理,构造了包含相邻两个时刻系统状态和未知扰动的量测方程.在此基础上,定义了递推上限滤波框架,以在线递推估计误差协方差的上限取代理论估计误差协方差的递推,以弥补未知扰动的影响.进一步地,将估计误差协方差上限的计算转化为标量参数的凸优化处理,以获得估计误差协方差最小上限的有效近似,从而实现有色噪声下最小上限滤波递推.后续研究应进一步考虑多拍量测噪声相关性,并利用多参数优化以获取更加准确的估计误差协方差的最小上限.同时,考虑实际系统在诸多场合建模为连续时间随机系统,可类比离散时间卡尔曼滤波和连续时间卡尔曼滤波之间的联系,在重点关注连续时间未知扰动建模的基础上,进一步研究将所提有色噪声下最小上限滤波推广到相应连续系统.

附录 定理1的证明

1)CUBF存在性证明.

因此,式(13)成立.

2)CMUBF存在性证明.

式(21)成立.