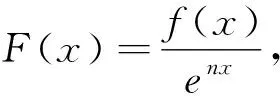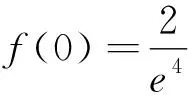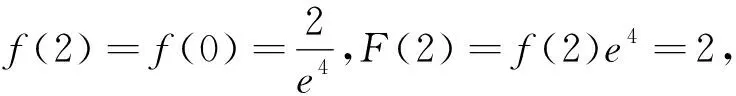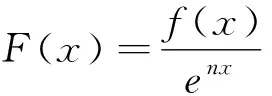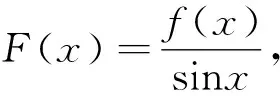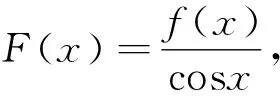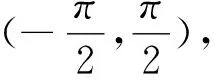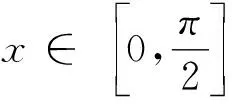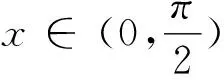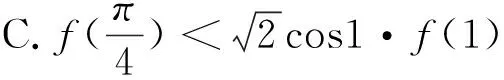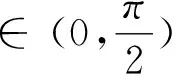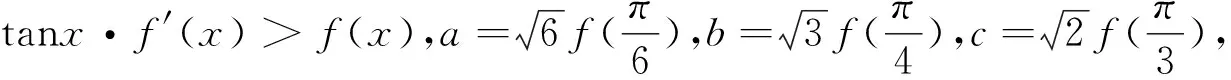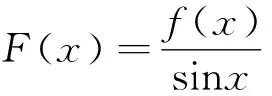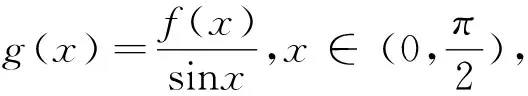数学建模视角下与导数有关的不等式问题妙解路径*

福建省永春县教师进修学校 (362600) 郑坚帜

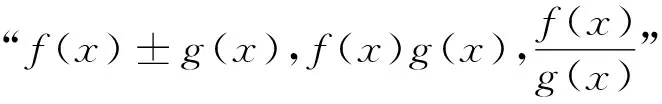
第一类 构造F(x)=xnf(x)(n∈Z,且n≠0)函数模型

(1)若F(x)=xnf(x),则F′(x)=nxn-1f(x)+xnf′(x)=xn-1[nf(x)+xf′(x)]．若题干出现形如nf(x)+xf′(x)的条件,可以构造函数F(x)=xnf(x);

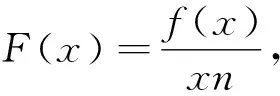
例1 (2021春·赣县区校级月考)已知函数f(x)的定义域为(0,+∞),f′(x)是f(x)的导函数,且满足f(x)>xf′(x),则不等式的解集为f(x2-1)>(x-1)f(x-1)．

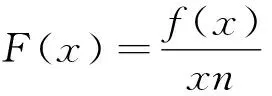
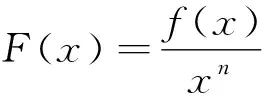
例2 (2022春·邹城市期中)已知奇函数f(x)是定义在R上的可导函数,且f(x)的导函数为f′(x),当x<0时,有2f(x)+xf′(x)<0,则不等式(x+2021)2f(x+2021)+4f(2)<0的解集为．

解析：当x<0时,2f(x)+xf′(x)>0,符合F(x)=xnf(x)模型.构造g(x)=x2f(x),当x<0时,g′(x)=2xf(x)+x2f′(x)<0,∴g(x)在(-∞,0)上单调递减①;∵f(x)是定义在R上的奇函数,∴g(x)=x2f(x)在R上为奇函数②,∴f(0)=0,g(0)=0,由①②得g(x)在R上单调递减,∴(x+2021)2f(x+2021)+4f(2)<0(2)⟺(x+2021)2

评注：抓住2f(x)+xf′(x)结构特点,构造F(x)=xnf(x)型函数模型．构造函数g(x)=x2f(x),求导分析g(x)为单调递减函数,将所求不等式转化为g(x+2021)

第二类 构造F(x)=enxf(x)(n∈Z,且n≠0)函数模型

(1)若F(x)=enxf(x),则F′(x)=n·enxf(x)+enxf′(x)=enx[f′(x)+nf(x)]．若题干出现形如f′(x)+nf(x)的条件,可以构造函数F(x)=enxf(x);

评注：抓住f′(x)+2f(x)结构特点,构造F(x)=enxf(x)型函数模型．构造函数F(x)=f(x)e2x,结合已知导数关系可得F(x)单调递增,然后结合函数图象的平移及对称性可求F(2),将不等式f(x)<2e-2x转化为F(x)

例4 (2022春·遂宁期末)定义域为R的可导函数y=f(x)的导函数为f′(x),满足f(x)>f′(x),且f(0)=3,则不等式f(x)<3ex的解集为．

(1)若F(x)=f(x)sinx,则F′(x)=f′(x)sinx+f(x)cosx．若题干出现形如f′(x)sinx+f(x)cosx或f′(x)tanx+f(x)的条件,可以构造函数F(x)=f(x)sinx;

(3)若F(x)=f(x)cosx,则F′(x)=f′(x)cosx-f(x)sinx．若题干出现形如f′(x)cosx-f(x)sinx或f′(x)-f(x)tanx的条件,可以构造函数F(x)=f(x)cosx;

A．a

C．b

与导数有关的不等式的客观题,通过构造函数法总结的三个模型,不仅加深考生对不等式与导数知识点的认识与理解,又使其在构建模型时更加全面地考虑问题,避免其在以后的解题中走弯路,提高解题的正确性.因此,高中数学教学过程中,应该重视经典例题剖析,从明确问题、合理假设、搭建模型、求解模型、分析检验、模型解释基本步骤渗透数学建模.在教学实践中,不断强化模型应用的条件,把握构建不同数学模型的关键点,解题少走弯路,达到化繁为简,学以致用的目的.