分时时差定位技术对系统定位精度影响分析

张玉喜,佟玉亮,张 夏,姜 琳

(1.中国船舶集团有限公司第八研究院,南京 211153;2.91709部队,吉林 珲春 133300;3.32064部队,浙江 舟山316000)

0 引 言

对于分布式(一主两辅)时差定位系统[1],时差定位技术须要3个侦测站同时截获到目标信号、得到两个主辅时间差,才能进行双曲线交汇时差定位,而实际上机载相控阵雷达受发射功率限制[2],其雷达波束较窄,发射的信号指向性较强,导致目标无法被3个侦测站同时截获,无法满足系统时差定位的基本需求。

针对上述问题,本文提出一种新型时差定位方法,即当定位系统中只有两个侦测站截获到目标信号、得到一个时间差时,通过将不同时刻的双站时间差进行时差匹配,得到一个错位时间差组进行双曲线交汇定位,形成目标的运动轨迹,文中简称“分时定位”。

1 分时时差定位技术原理

传统分布式时差定位系统[3-4]由主基站A(xA,yA,zA)与两个辅基站B(xB,yB,zB)、C(xC,yC,zC)构成。假设目标辐射源坐标P(x,y,z)。

由图1中的简单几何关系可知:

图1 时差定位原理示意图

rA-rB=ΔtAB·v

rA-rC=ΔtAC·v

(1)

式中,ΔtAB=tA-tB、ΔtAC=tA-tC分别为对应基站之间的接收信号到达时间差;rA、rB、rC分别为目标辐射源到基站A、B、C的距离;v为信号的传播速度。

将式(1)改写为

=ΔtAB·v

=ΔtAC·v

(2)

考虑远距离目标,目标高度的影响可忽略不计,转化为二维平面内,则有

z=zA=zB=zC=0

(3)

假设原点处于AB段中点,且x轴与AB线重合,将式(2)中的第1个方程继续转化为

(4)

对式(4)推导变形后得到

(5)

由于式(5)是一个双曲线方程,故式(2)可化为两个双曲线方程,组成一个双曲线方程组,求出其交点即为目标P点的位置。

上述理论为常规时差定位的Chan算法数学模型[5],针对目标信号未被3个侦测站同时截获到而无法得到主辅时间差组(ΔtAB,ΔtCB)时,考虑先将已有的单边时间差ΔtAB存储下来,在时间窗阈值范围内与后续接收的另一个单边时间差ΔtCB进行时差配对,形成新的时差组,完成时差定位。

图2给出了分时定位时差匹配原理。假设C站存在部分信号未接收,原本(A1B1,C1B1)为一组时间差组,但由于C1未收到,拟通过将时间差A1B1存储下来,与时间差C2B2进行配对,错位匹配的时间间隔为T,利用(A1B1，C2B2)时间差组进行目标时差定位。

图2 分时定位时差匹配原理示意图

采取不同时刻的信号到达时间差值进行匹配必然会带来少量的定位位置偏差,故有必要寻求一个合适的错位匹配时间窗阈值范围。本文研究在不同时间窗阈值下,非同时刻双站时间差配对成的时差组对目标定位精度的影响,并考察在该定位模型下目标与站点的距离方位关系,以及目标自身的运动轨迹对系统定位精度[6-7]的影响。

2 技术可行性分析

本技术主要针对机载辐射源目标[8],目前航空器最大飞行速度一般为500 m/s,时差定位系统在秒级范围内进行不同时间段的时差配对。如图3所示,P点为目标的真实位置,由于BC站时间差滞后错位配对,使得BC站对应的时差曲线相应发生偏移,与AB站对应的双曲线相交后得到新的交点P’,故引入了目标定位误差值。考虑结合目标的最大运动速度,该时差定位方法产生的定位偏差值约为几至十几公里,可大致满足目标的定位精度需求。

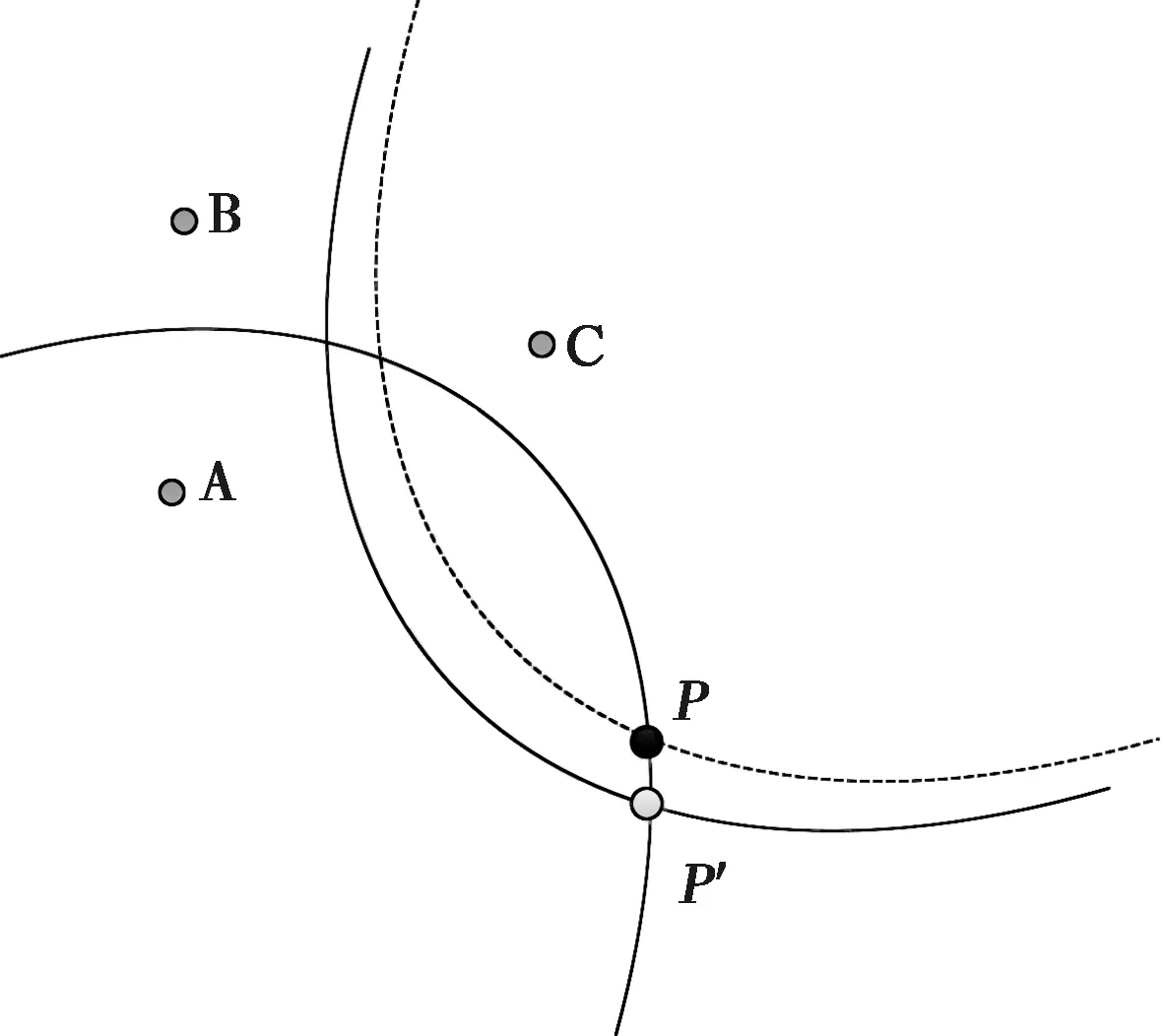
图3 双曲线交汇定位示意图

3 仿真研究

通过Matlab软件开展仿真试验,建立数学模型,一主(B)两辅(A、C)站址分布模式,站间基线长度为28.2 km,基线夹角为90°,具体布站方式如图4所示,目标的最大运动速度为500 m/s,仅考虑目标在系统侦测覆盖区域夹角内运动。

图4 站址分布图

3.1 不同的错位匹配时间条件

研究不同错位匹配时间下对系统定位误差的影响,目标在距离主站约200 km附近沿X轴方向运动,比对真实轨迹与定位轨迹。

当时差错位匹配时间为0.5 s、1 s、2 s、3 s、4 s时,目标定位轨迹与真实轨迹对比结果分别如图5～9所示,其目标定位相对偏差分别为1.18%、2.39%、4.9%、7.55%和10.34%。

图5 系统定位效果图(时差错位匹配时间0.5 s)

图6 系统定位效果图(时差错位匹配时间1 s)

图7 系统定位效果图(时差错位匹配时间2 s)

图8 系统定位效果图(时差错位匹配时间3 s)

图9 系统定位效果图(时差错位匹配时间4 s)

可以看出:时差错位匹配时间越长,系统的定位误差就越大,这与理论分析一致。

由于在该场景下系统无法进行常规分布式时差定位,通过采用该分时定位技术完成对目标的补充定位,保证系统对目标整个跟踪轨迹的完整性。根据仿真结果,当系统的时差错位匹配时间最大值约为2 s时,系统的定位精度误差小于5%,以牺牲部分定位精度为代价达到了对目标连续稳定跟踪的目的。

3.2 目标不同的运动状态

本节的仿真分析参数均假设时差匹配错位时间为2 s,主要从目标与侦测站的位置距离、方位两个方面分析目标不同运动状态下对系统定位精度的影响。

3.2.1 目标距离不同

目标沿X轴方向直线运动,研究目标与主站不同距离下的定位误差关系,仿真结果如图10所示,进而得到各个距离下目标定位的相对误差如表1所示。

表1 目标沿X轴方向直线运动时不同距离下的定位误差

图10 目标沿X轴方向直线运动时系统定位误差与目标距离的关系

目标距主站距离越远,系统定位误差就越大,且定位误差变化为非线性变化,目标距离越远,误差变化率越小,最终定位误差将收敛于一个固定值。

3.2.2 目标处于不同方位

(1)目标沿Y轴方向直线运动

研究目标处于主站不同方位时目标定位误差关系,仿真结果如图11所示,进而得到对应目标定位的相对误差,结果如表2所示。

表2 目标沿Y轴方向直线运动时不同方位下的定位误差

图11 目标沿Y轴方向直线运动时系统定位误差与目标位置的关系

(2)目标保持与主站固定距离做圆周运动

目标处于系统探测区域内目标定位与其所处方位之间的误差关系如图12所示。目标离系统探测区域中轴线越近,系统定位误差越小,定位效果越好。

(a)系统定位误差

由本节两个仿真结果可知,无论目标沿一个方向直线运动或者做曲线圆周运动,目标距系统探测区域中轴线越远,系统定位误差就越大;当目标沿探测区域中轴线方向附近做直线运动时,系统对目标的定位误差几乎可以忽略不计。

3.2.3 目标其他运动方式

(1)目标沿斜向方向作直线运动

得到目标的定位结果如图13所示,目标整体运动轨迹与侦测区域中轴线较远的定位精度小于靠近中轴线的运动轨迹,因此目标所处方位对该系统定位精度的影响权重大于目标与主站的距离所带来的精度影响。目标定位的误差结果如表3所示。

表3 目标沿斜向做直线运动时定位误差

图13 目标沿斜向运动时系统定位误差效果图

(2)目标在探测区域内做圆周运动

以(100,350)为圆心,运动半径为150 km,目标进行一次完整的圆周运动轨迹时得到目标定位结果与真实轨迹对比如图14所示。该系统模型给出的整体定位结果误差约为 2.65%,可满足设备实际运用的指标需求,同时验证了3.2.1节中目标距离越远定位误差越大的结论。

图14 目标圆周运动时系统定位精度效果图

3.3 仿真小结

本章通过在不同错位匹配时间条件下对目标轨迹进行定位跟踪,得出对应的系统定位精度关系,根据工程经验选择了合适的错位匹配时间作为匹配时间阈值。同时在该阈值下,对不同运动状态的目标进行仿真分析,模拟了目标与主站在不同位置距离、方位等情况下系统的定位精度效果,结果表明目标距离侦测站越远,方位越偏离侦测中心区域,系统的定位误差就越大,这也与常规的Chan算法时差定位模型结论一致,进一步验证了该时差定位技术的可行性。

4 结束语

本文提出一种新型时差定位方法,通过在不同错位匹配时间条件下对系统的定位误差进行分析,得出合适的错位匹配时间阈值上限;在此参数基础上,通过对目标处于不同距离、方位等情况进行误差仿真分析,研究了系统对于各种状态下目标的定位精度效果。针对实际工程技术指标,按照其侦测目标位置和定位精度需求,选择合适的错位匹配时间阈值进行分时定位,以便满足系统定位和连续跟踪的任务需求。