基于Netlogo的舆论动力学模型的研究

周艳玲,沈晓轩

(合肥学院 人工智能与大数据学院,安徽 合肥 230041)

0 引言

近年来互联网信息技术高速发展,网络已经成为反映社会舆情的主要载体之一,政府行政问政的渠道更多通过网络上舆情,对网络舆情开展监控工作,可以有效提升政策制定的针对性和准确性[1]。网络舆情是指在互联网上流行的对社会问题不同看法的网络舆论,是社会舆论的一种表现形式,是通过互联网传播的公众对现实生活中某些热点、焦点问题所持的有较强影响力、倾向性的言论和观点。网络舆论则是各种流行网络舆情的多元化集合和新时期社会治理的重要基础数据资源[2]。舆论动力学最近备受关注,在该领域已有大量成果,舆论动力学旨在探讨舆论生成与演变的内外动因,挖掘观点转变与共识形成的普遍规律[3]。同时,新型冠状病毒肺炎大流行的发生极大地促进了网络舆情的研究[4],并且舆论动力学的研究对理解、控制和优化真实系统有着重要的现实意义,也为理解人类的行为模式提供了一个独特的视角[5],研究者常用复杂网络方法研究舆论动力学过程并提出了诸多模型,如F-J模型、D-K模型、Deffuant模型和KH模型等,其中Deffuant模型和KH模型都为有限信任模型,即存在一个置信区间(阈值),只有差距在阈值内个体才会相互影响,但Deffuant模型与KH模型有所区别,Deffuant模型是每个时刻选取一对相邻网络节点进行交互,而KH模型每个时刻选取社交网络的某个个体与满足阈值范围内的所有个体进行交互。因此,本论文选择KH模型建立复杂网络,构建无标度的社交网络,并对阈值提出新的要求,使得传播网络的实现更为贴近现实舆情的传播情况。同时,通过Netlogo仿真环境对网络舆情在无标度网络上的传播进行实时监测,由于环境变化及舆情引导工作的开展,网络舆情传播会出现相应的变化,从而本文将正常舆情传播分为三个阶段:发生期、爆发期和平息期。运用大数据去分析各阶段的数值波动,对监测到的有价值信息进行深度的思考加工和分析研究,更有效地制定出切实符合大众利益的公共政策[6]。

1 舆情监测系统的仿真模型构建

1.1 舆情传播网络概述

新媒体信息革命催生出了强大的网络力量,网络舆情的形成与社会性网络信息的传播密切相关[7]。现实世界的网络大部分都不是随机网络,少数的节点往往拥有大量的连接,而大部分节点却仅有很少的连接,其中社会人际关系网络更为复杂,较为符合复杂网络中无标度网络的情形。无标度网络具有普遍性,但同时也具有严重的异质性,其各节点之间的连接状况具有严重的不均匀分布性:网络中少数称之为Hub的节点的度数大,大多数节点的度数比较小,其中Hub节点在运行中起主导作用。因此本模型网络构建时,选用简洁的无标度网络构建模型,即BA模型。

BA模型遵循两个机制:

增长:每次加入一个新的节点,模拟显示网络不断增大变大。

优先连接:在新节点加入时,优先选择与高度数的节点连接。这模拟现实中新网页一般会连接到知名的网络站点,如新机场会优先考虑建立与大机场之间的航线。i和j节点连接概率算法:

(1)

Ki为i节点的度,分母为所有已有节点的度之和。

但是在BA无标度网络中,每个新节点的度值相同,优先连接概率与原节点的度值呈线性关系,原节点之间无法产生新的连接,且网络聚类特性较差[8]。因此本模型网络对BA无标度网络进行优化衍生,将机制中的优先连接中的概率算法改为欧几里得距离,即所创建的网络是基于节点之间的接近性。欧几里得距离算法公式:

(2)

同时,为了保证原节点的可重用性与网络的聚类特性更贴近舆情传播网络,引入聚类系数,控制整个网络图的平均节点度数。网络节点间的距离调用Netlogo自带的layout-spring方法,使整个网络看起来更加美观。

1.2 舆情监测模型SIRKH模型建立

SIRKH模型是基于舆论动力学模型KH模型和传统流行病传播模型SIR模型而改进的舆情监测模型。传统SIR模型分为三类人群:易感者S、感染者I和康复者R,其中感染者会有概率感染易感者,也有一定概率会变为康复者。KH模型是有限信任模型,即存在一个置信区间(阈值)只有差距在阈值内才会相互影响,每个时刻选择某个节点与所有观点值在阈值范围内的节点交互,以此模拟现实舆情点的传播方式,控制传播概率。

SIRKH模型,将舆情传播网络中的人群分为四类:易受谣言影响者S、媒体谣言传播者O、个人谣言传播者P和免疫谣言者R。媒体和个人谣言传播者有概率传播谣言给易受谣言影响者,该概率即为KH模型制定的置信区间(阈值),为了使阈值更符合舆情传播概率,添加热值参数,热值越高,阈值就越大,就更易传播。

SIRKH模型的仿真模型中黄点代表非媒体影响的个人谣言传播者,红点代表受媒体谣言传播影响人群,蓝点代表易受谣言影响者,灰点代表康复者,热值hot会影响红点与黄点的颜色,相邻节点谣言传播者越多,热值越高,颜色就越深;模型有七个滑块组件:number-of-nodes滑块用于调节舆情传播网络中的节点数,符合BA模型的增长机制;average-node-degree滑块控制平均节点度数,并与number-of-nodes滑块一起改变网络节点连接数;initial-outbreak-size滑块控制初始舆情点数量,媒体舆情点和个人舆情点根据舆情点的初始热值来随机产生;rumors-spread-chance滑块与hot参数一起控制舆情的置信区间;rumors-check-frequency滑块用于调节舆情的检查频率,实现舆情的实时监测;recovery-chance滑块控制谣言传播者转变为易受谣言影响者的概率;gain-resistance-chance滑块控制谣言传播者转变为谣言免疫者的概率。

1.2.1 SIRKH模型符号说明

构建SIRKH数学模型所需的符号如表1所示:

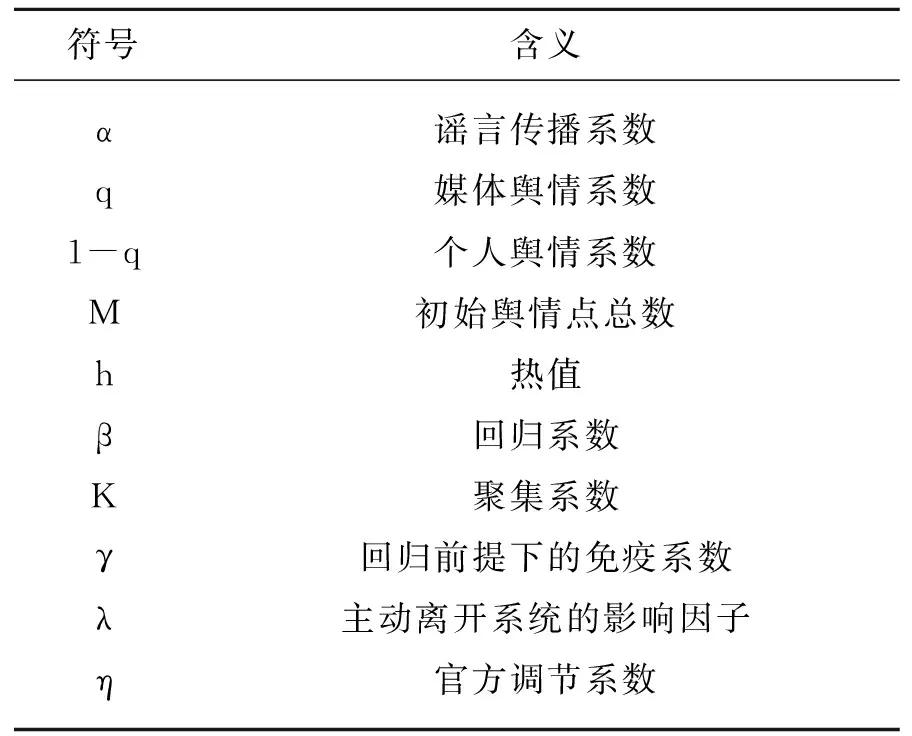
表1 模型符号表

1.2.2 SIRKH数学模型的构建

建立SIRKH中舆情动力学数学模型,即Agent之间的意见交互规则,该规则要求能够体现出意见变化的各种因素。本模型是用0～1之间的连续值代表网络中每个节点的舆论值,Si表示i个节点的舆论值,用ε=α+αh∈(0,1)表示网络中邻接节点的信任条件,若邻接节点的舆论差小于ε,则表示两者相互信任,两者达成共识。反之,如果两者的舆论差大于ε,则表示两者互不信任,由于本模型中|Si(t)-Sj(t)|的值会受外部环境影响因子影响,所以将其设置为0～1的随机值,将每个节点的热值h设置为阈值ε的系数。演化规则如下:

当|Si(t)-Sj(t)|≤ε时,下一时间步按照以下方式改变节点对的意见。

S(t+1)→O(t+1)(若前置agent为O:媒体谣言传播者)

S(t+1)→P(t+1)(若前置agent为P:个人谣言传播者)

S(t+1)表示下个时间步节点的意见状态。图1为SIRKH模型状态图。

图1 SIRKH模型状态图

(2) 代入时间参数t后,对SIR数学模型进行优化改进,引入舆论动力学数学模型,在传统传播谣言模型的基础上,考虑媒体传播和个人传播外部影响因素不同,因此设置影响因子λ和η。构建的SIRKH数学模型的微分方程如公式3-公式7所示:

(3)

(4)

(5)

(6)

S(t)+I(t)+R(t)=1;I(t)=O(t)+P(t)

(7)

本模型描述的是舆情传播过程中每一时刻邻接矩阵节点状态的变化。从节点的初始状态到节点的最终状态,由易受谣言影响者接触到信息在置信区间内转化为传播者,再到传播者受环境影响因子影响会对信息产生质疑从而回归到易受谣言影响者,而当传播者已经确认信息的不实,则会变为免疫谣言者。

2 Netlogo下的SIRKH模型分析与仿真

2.1 SIRKH模型初始化参数

基于复杂网络最基本的三大特点——小世界、无标度、高聚类,本模型中的舆情传播网络就属于复杂网络,为了方便仿真模拟舆情传播过程中主体交互,状态的变化,对模型的参数进行初始化,如表2所示:

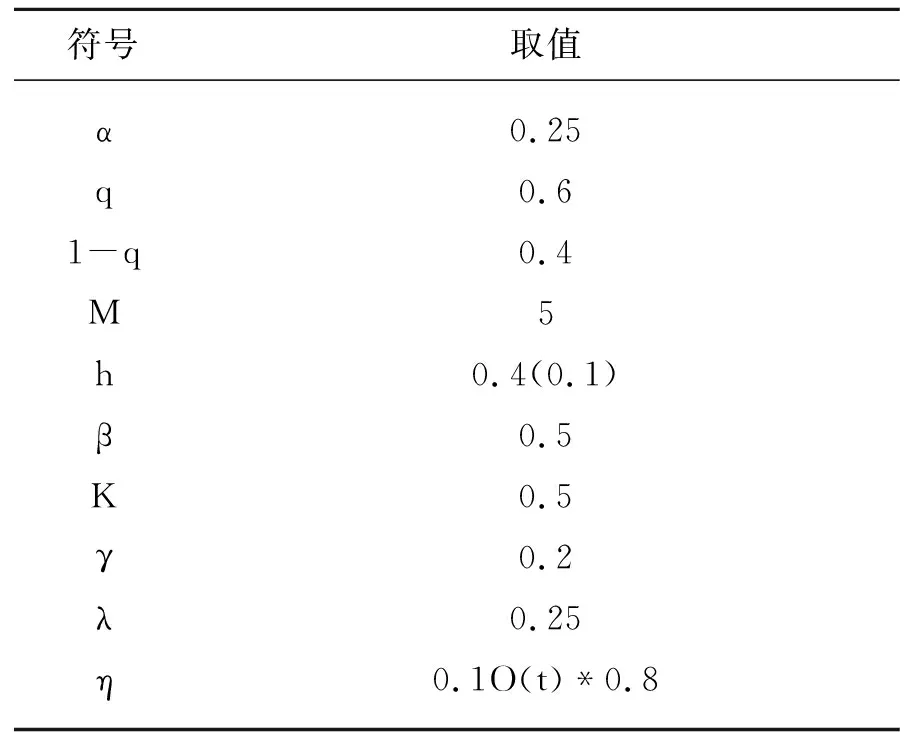
表2 模型参数初始化表

本系统初始时默认不存在免疫谣言者,其中N,M,α,β,γ均可通过Netlogo中的滑块组件进行调节,使数据变化更灵活。同时为了保证数据来源的可靠,随机选取校内150人分别对5个舆情的观点进行的实际问卷调研,根据调研结果对谣言传播系数α、回归系数β、回归前提下的免疫系数γ、主动离开系统的影响因子λ分别设置初始值。为了实验数据的合理性,媒体舆情系数q的初始值应高于个体舆情系数1-q,聚集系数初始值设为0.5是使无标度网络图更为贴近实际社交网络。热值h是Agent的内置参数会受邻接节点的状态影响,因此媒体的热值要比个人热值高,同时媒体传播的热值过高也会被官方介入压低热值。在媒体舆情热度过高时,官方介入,引入官方调节系数η,η是关于时间t的函数,本模型中官方调节系数中的媒体谣言危害度调节为0.8。

2.2 初始状态下的仿真模拟分析

模型场景初始时,舆情传播网络中通过组件分别调节区域主体数为150,平均节点度数为7,聚集系数为0.5,节点连接数为525。舆情初始阶段,只有五个舆情点,其中三个媒体舆情点,两个个人舆情点,为了确保实验的合理性,针对媒体舆情点的选取通过对邻接矩阵遍历,从中选择出三个度数最大的节点,而个人舆情点是通过除媒体舆情点外的节点随机选取。同时,为了保证实时监测,设定舆情传播频率为1ticks,ticks的单位以小时计。传播过程节点的状态变化,根据上述的SIRKH模型状态图以及参数的值来确定。舆情传播结束的标志为视图中没有谣言传播者的存在。

进一步观察Netlogo仿真软件中的视图,发现滑块参数设置与上述描述一致,保证了数据的准确性。在Netlogo的舆情传播网络中可以观测到没有独立的节点,并且可以发现运行结束时,模型中中不存在谣言传播者,即舆情点。综上所述,舆情传播过程符合预期设想。

进一步观察舆情监测系统的网络图,其中的数据均是从Netlogo软件仿真模拟初始化情形下的舆情传播一个周期中的网络图数据中导出到EXCEL表中,再经过数据处理,生成的舆情传播数据图如图2所示。主坐标轴用于反馈S易受谣言影响者和R免疫谣言者的数量,次坐标轴用于描述媒体谣言传播者和个体谣言传播者的人数。

图2 舆情传播数据图-初始状态

由图2可知舆情传播的整个过程持续386个小时,易受谣言影响者的人数总体呈现下降的趋势,但在180个小时后会有所回升,最终数据停在70人,可推知是收到舆情热度下降和谣言传播者自觉脱离系统的影响;免疫谣言者的数据一直呈现上升的趋势,最终达到80人;媒体谣言传播者和个人谣言传播者的数据起伏不断,但总体可将其分为三个阶段:发生期、爆发期、平息期,媒体舆情的发生期在0～100小时,爆发期在100～195小时,在122小时达到峰值42,之后数据呈现下降趋势进入平息期;个人舆情的发生期在0～54小时,爆发期在54～133小时,在70小时达到峰值14,之后进入平息期,由数据可知,两种舆情发展总体都呈现先上升后下降的趋势,媒体舆情周期长于个人舆情,并且影响程度也更大,结果符合实际预期。

2.3 抑制舆情传播方式仿真场景分析

2.3.1 控制舆情传播网络场景

对于不好的言论,须将言论的影响降到最低,传播范围尽量控制到最低,因此本论文先从传播网络入手,减少舆情传播网络中节点的连接,即减少舆论在社交网络之间的传播。现如今的网络工具,微信、QQ等应用软件使舆论传播更加简单,也将很多陌生人联系在一起,扩大了人们的交际网络,使舆论更加难以控制。因此,必须对此加以管制,从而达到通过控制传播网络,减少舆论的传播。若区域内人数不变的情况下,将此策略用Netlogo仿真,即需通过average-node-degree滑块减少平均节点度数或降低聚集系数,本次仿真实验通过减少平均节点度数。

从Netlogo仿真软件中的运行结果可知,在主体个数与聚集系数不变,将average-node-degree滑块减少至6时,将节点总连接数降为450,其余的条件与初始状态保持一致,符合预期设想。

观察舆情监测系统运行时数据的变化,其中的数据均是从Netlogo软件仿真模拟控制传播途径情形下的舆情传播一个周期中的网络图数据中导出到EXCEL表中,再经过数据处理,生成的控制舆情传播网络场景的数据分析图如图3所示。主坐标轴用于反馈S易受谣言影响者和R免疫谣言者的数量,次坐标轴用于描述媒体谣言传播者和个体谣言传播者的人数。

图3 控制舆情传播网络场景的数据分析

从图3可知,舆情传播过程持续了241个小时,相比于初始状态有了明显的下降。易受谣言影响者的人数在57小时左右有一段明显的上升,而此时媒体谣言传播者和个人谣言传播者都处于低谷,可知在部分人对谣言产生了质疑;免疫谣言者人数一直处于上升状态;媒体谣言传播者出现了两次爆发期分别在35小时与81小时左右,最高值分别达到21与25,并在132小时后渐渐平息;个人舆情在16～42处于爆发期,最高值为7。与初始状态相比,无论是媒体舆情还是个人舆情传播周期都缩短了,传播的范围甚至降低了近一半。因此,从数据变化可知,当我们从传播媒介入手,减少舆情传播网络的节点联系后,可以达到抑制舆情传播的效果。结果符合实际预期。

2.3.2 舆论动力学原理抑制舆情仿真场景

本模型是建立在舆情动力学模型KH基础之上,而KH模型为有限信任模型,即Agent之间存在一个置信区间(阈值),主体之间只有在置信区间内才可完成交互,因此想要抑制主体间的舆情传播可通过缩小置信区间,让主体间更难实现交互,从而使舆情不能在主体间传播。置信区间(阈值)与舆情的热值和谣言传播系数相关,因为热值是舆情本身的属性,热值的大小是一个不定值,不容易调控,所以我们可通过舆论知识宣传等相关方式,降低谣言传播系数,从而达到缩小置信区间的效果。

从Netlogo仿真软件中可以观察到,通过rumors-spread-chance滑块将谣言传播系数降到20%,来模拟通过舆论知识宣传等相关方式进行控制置信区间,其余的条件与初始状态相同进行仿真模拟,舆情传播过程顺利,符合预期设想。

对舆论动力学原理抑制舆情仿真场景的传播过程进行数据分析,其中的数据均是从Netlogo软件的网络图数据中导出到EXCEL表中,再进行数据处理,生成的舆论动力学原理抑制舆情场景数据图如图4所示。主坐标轴用于反馈S易受谣言影响者和R免疫谣言者的数量,次坐标轴用于描述媒体谣言传播者和个体谣言传播者的人数。

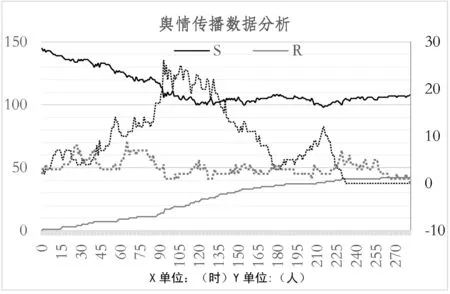
图4 舆论动力学原理抑制舆情场景数据分析

从图4可知,舆情传播过程持续了281个小时,相比于初始状态传播周期明显缩短。易受谣言影响者的人数在总体呈现下降趋势,最终人数稳定在108;媒体谣言传播者爆发期在86～142小时,最高值达到25,比起初始状态下的42人,下降明显,并在143小时后渐渐平息虽然后期有所起伏,但人数并不多;个人舆情在27小时和65小时分别达到波峰,最高值分别为8和9。与初始场景相比,由于降低了舆论动力学原理中的KH模型的置信区间,发现舆情监测系统的周期明显有所缩短,舆情的影响范围也有所降低。因此,本次仿真模拟通过降低谣言传播系数来影响舆论动力学原理中的置信区间,从而实现对主体间交互规则的影响后,成功减少了Agent之间的交互成功率,达到了抑制舆情传播的效果,结果符合实际预期。

3 结果分析

根据上述SIRKH模型在不同场景的舆情传播仿真模拟实验的数据分析,可以分别从舆情潜伏期、发生期和爆发期三个阶段入手,分析上述不同影响因素下的仿真场景结果,从而对舆情采取合理引导与管制措施,以此来提升社会幸福感。根据重要程度排序,每一阶段的问题严重程度和应对策略重要程度基本一致。

首先,在舆情的潜伏期,这个阶段控制不好容易导致初始舆情点增多以及舆情突然爆发。由于舆情具有开放性和引导性,如果区域主体对其缺乏认知,那就容易在舆情出现时,出现大量的盲目性传播,从而使舆情一出现就达到高峰,甚至无法控制。因此需要防患于未然,进行舆论引导,如通过知识宣讲,定期开设舆情事件的宣讲,增加群众的认知或向群众反映即将可能出现的舆情事件事实,使群众可以判断出舆情的真伪。本模型在准备阶段就加入了主体的影响因子,即学历(见识),将主体的见识分为四个等级,等级越高,对舆情的置信度就越低,通过在Netlogo中更改主体的学历(见识)来模拟群众的见识,见识高的主体会主动离开舆情系统。为了贴近现实,上述三个场景,主体的见识都是四个等级随机生成,若都改为更高级,个体舆情传播周期将更短。

在舆情的发生期,这个阶段的舆情已经发酵,想要控制舆情的发展趋势需要从媒介进行管控,舆情传播网络中主体交互的特点就是必须主体之间已经建立起联系,因此若减少主体间的联系,或者减少区域主体的聚集系数就可以对舆情的发展进行管控。本文的控制舆情传播网络场景就是通过减少主体间联系来实现舆情管制,可以发现效果很显著,舆情传播周期与范围都缩小了近一半,而减少聚集系数也就是在减少主体之间的密度,从而减少主体间的联系,因此减少聚集系数也可以达到管制疫情的效果。同样,减少主体之间的交互频率也是一种方式。本文的舆论动力学原理抑制舆情仿真场景就是通过减少置信区间,从而使主体之间的交互频率降低,通过上述数据分析结果可知,此方式可以抑制舆情的发展状况。

在舆情爆发期,舆情对主体的影响较大,若不采取强制管制措施,可能会导致舆情持续发酵,热度居高不下,甚至影响社会的稳定。本文就引入舆情的热值参数,热值会随着周边传播者聚集情况进行改变,当热值过高时,官方会进行紧急公关,在热值预警值调低后,可发现媒体舆情传播周期与影响范围都有所降低,有利于将舆情向积极良性的方向发展。

4 结语

本文主要介绍了一种基于Netlogo的舆情监测系统,通过对传统病毒传播模型SIR进行舆情分析方向上的优化并在其中融入修改后的舆论动力学KH模型,构建舆情监测SIRKH模型。目前,网络舆情监测的方式主要以系统自动方式为主、人工二次筛选为辅。随着大数据时代的到来,如何进一步优化舆情分析系统是研究者普遍需要思考的问题。本文主要内容是采用Netlogo对舆情发展进行仿真分析,在仿真场景中加入影响因子,如舆论动力学的交互规则、主体所在的社交网络、主体的学历等,并通过对舆情发展的各主体状态的实时数据分析,探究从传播网络和舆论动力学原理两个方面如何抑制消极舆情的传播,并通过对仿真结果分析,并将其应用到现实中的舆情监测。