有效反思 助力成长

邓芸芸

［摘  要］ 文章以某区小学数学青年教师学科专业水平测试的情况为例，分析青年教师在知识掌握中存在的一些典型问题：对教材的理解分析不深刻、对课标要求不熟悉、对学科知识体系没有结构化的认知、对数学学科相关知识不精通等。青年教师只有加强对课程标准与教材的深度解读，熟知学科大循环体系，在“高观点”下审视初等数学的知识，并形成结构化的认知，才能有效实施教学，提升学生的核心素养。

［关键词］ 小学数学教师；学科水平；测试分析

有效的教学依赖于教师对数学知识的深刻理解。教育家苏霍姆林斯基曾指出：教师教育素养的第一要素，就是要熟知学科内容并且绰绰有余。的确，学科知识水平在教师的教学水平上起着关键性的作用。因为任何人都无法教给别人他自己都不懂的东西。可以说，培养青年教师的根本，就在于提高他们的专业知识，这应是教学的“内功”。

下面就以某区小学数学青年教师专业知识测试情况为例，谈一谈目前普遍存在的一些问题，并尝试分析原因，寻找对策。

一、背景介绍

这次测试的对象是区内工作3年内的新教师，测试的内容主要包含这几类问题：1. 数学史；2. 小学数学基本知识（包括教材例题，教材知识点，教材思考题，课标题）；3. 教材体系题; 4. 学科素养拓展题。

二、问题呈现

1. 典型问题1

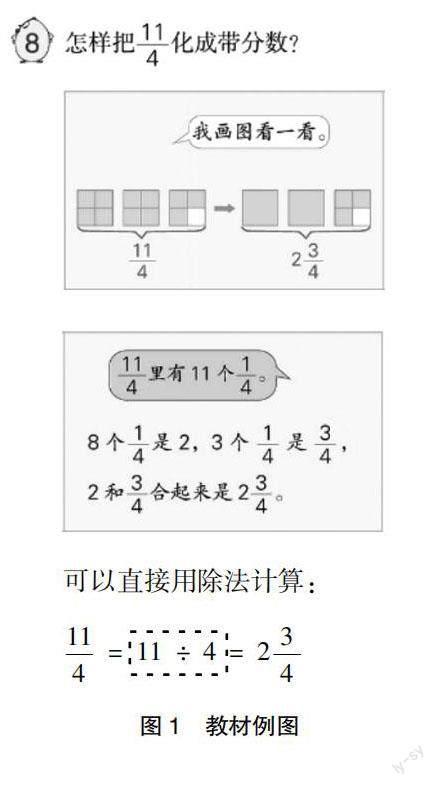
怎樣把11/4化成带分数？你能想出哪几种方法？（至少写出两种）

这是苏教版数学五（下）的一道例题。例题是教材中的重要内容，教师对教材例题的理解水平，直接影响着课堂教学的质量。教材中呈现的方法，第一种是图形表征，第二种是语言表征，第三种是算式表征，前两种可以看作是第三种除法计算的算理。借助多元表征可以帮助学生从不同的角度来理解数学概念，促进数学思考。教师1和教师2体现了不同的表征，思维的发散度也比较高；教师3和教师4可以看作一类，方法单一。在118位教师中，能答出两种以上的占61%，超过1/3的青年教师只能答出两种以内。

2. 典型问题2

李阿姨去商店购物，带了100元。她买了2袋面，每袋30.4元；又买了1块牛肉，用了19.4元；她还想买1条鱼，大一些的鱼每条25.2元，小一些的鱼每条15.8元。请你帮李阿姨估计一下，她带的钱够不够买小鱼？能不能买大鱼？

图7  教师6答题节选

这是课程标准中的原题。教师5（如图6）答得比较好，是根据买大鱼和小鱼，分别选择了“去尾法”往小里估、“进一法”往大里估，体现了方法的灵活性和针对性。非常遗憾的是，竟然有19名教师没有采用估算的方法，比如教师6（如图7），他选择了精确计算。这说明这19位老师一方面不熟悉课标，另一方面估算意识比较薄弱。想一想，如果教师自身的估算意识不强，如何能引导学生主动估算呢？当然跟精确计算相比，估算的确要求更高，既要判断是否适合估算，又要选择合适的方法，并根据估算的结果进行判断，对学生思维的灵活性、发散性以及数感都有较高的要求。正因为如此，教师在平时的教学中，要更多地为学生提供一些可以估算的素材，引导学生主动尝试估算，让估算真正服务于实际问题的解决，体现估算的优势和价值，从而提高学生的估算意识和估算能力。

3. 典型问题3

小学阶段你学习了哪些平面图形的面积公式？请你用图示简单梳理一下这些公式的推导过程。

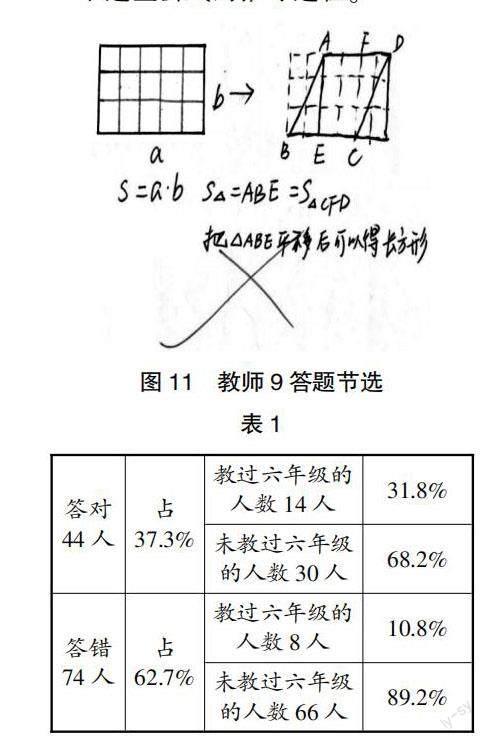
这道题是苏教版六（下）总复习中的内容。答题情况统计（如表1），118人中答对的只有44人，占了37.3%，有问题的占了62.7%，整体情况不佳。答对的人中有教过六年级的，占了31.8%，还有68.2%的教师没有教过六年级，这部分教师不仅熟悉本年级的教材，对其他年级的教材也比较熟悉，对整个平面图形面积计算方法的脉络都了然于心。在答错的人中，有89.2%没有教过六年级，这很好解释，因为没有教过六年级，所以没有答好。但是，作为一名数学教师，是否只是熟悉所教年级的教材就可以了呢？还是应该有更高的站位呢？只有教师心中有全局，知道学生的学习从哪儿来，将要到哪儿去，才能在教学时更准确地把握住教学的重难点，这样才有利于学生后续学习，促进学生的可持续发展。然而10.8%教过六年级的教师出错就实在让人遗憾。

4. 典型问题4

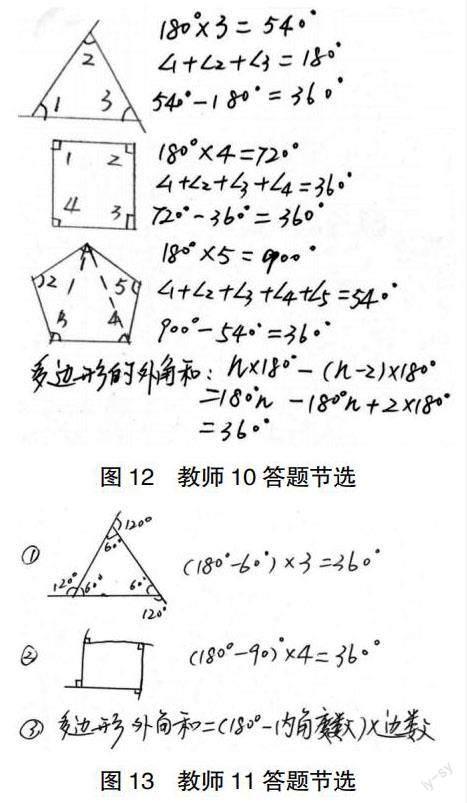
请写出探索多边形外角和计算方法的过程。

图12  教师10答题节选

图13  教师11答题节选

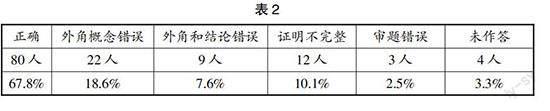
这道题对于小学生来说是拓展题，对于数学学科来说是初中八年级上册的知识点。如表2：其中80人答得比较好，占67.8%；有22名教师把外角的概念理解错误，错误地认为外角与对应的内角的和是360°；有9名教师外角的概念理解正确，但没能找到多边形的外角和；有12名教师没有完整的证明过程，采用了不完全归纳法。推理是重要的数学思想方法，推理包括合情推理、演绎推理。不完全归纳法属于合情推理，根据某几个例子，找到它们的共同特征，并推想这一类事物都具有这样的特征；合情推理主要意义在于发现新的命题，探索未知的规律，得到的结论具有或然性，不能用于证明；演绎推理是由一般到特殊的推理形式，推论前提与结论之间的联系是必然的，是一种确定性的推理。一个数学规律的证明必须经过严密的演绎推理来完成，只有这样这个结论才是公认的、可靠的。对于小学阶段的学生来说，他们只需掌握合情推理这种推理形式，但是教师必须对两种推理方式应有准确的理解和把握。

三、几点启示

根据这次区内教师学科专业水平测试的情况，笔者有以下几点粗浅的想法。

1. 加强对课程标准与教材的分析与解读

课程标准与教材，是教师教学中最重要的依据。课程标准解读与教材分析，应是青年教师的必修课程。对于课程标准和教材的内容，教师应做到谙熟于心。教材分析能力是合格教师必备素养之一，要能从“学什么”“教什么”“怎么学”等问题出发来分析教材，要在数学本质的观照下认真思考教材，明晰知识生发的脉络。如果教师不深入分析教材就开展教学，学生的学习很可能就偏离内容的本质，与数学素养的培养背道而驰。读教材不能仅停留在文本学习的层面，更要解读文本背后蕴含的教学理念与数学思想。日本数学教育家米山国藏提出，学生走出学校后，数学的公式可能会忘记，但数学思想方法会对他们终身有用。数学思想是从哲学的高度对数学的认识和理解，它基于数学知识，但又远远超越数学本身，具有极高的育人价值。青年教师应将教材中蕴含的数学思想方法充分挖掘后，融入教学设计与教学实践中。

2. 在“高观点”下审视初等数学知识，向深处延伸

在教学中，教师还要对所教的内容进行深度挖掘。教材里的一道题如果是给学生做，教师的教学该停留于哪一步？教师不能只局限于会做题，而应再深入“挖一挖”，思维往更深层次走一走。假如教师经常“挖一挖”，不仅可以深化自身的思维，而且还可以提升学生的思维深度。郑毓信教授曾在《数学教师的三项基本功》中提出：“我提倡一题一课，一课多题，一节数学课做一道题目，以一道题为例子讲解、变化、延伸、拓展，通过师生互动、探讨、尝试、修正，最后真正学到的是很多题的知识。”教师不应局限于为学生准备教材中的例题和练习，应结合知识的前后体系，多准备一些变式题、拓展题。这样一方面，能帮助学生疏通知识体系，另一方面，能使教师本身不只停留于所教教材，还着眼于课程，着眼于数学思想方法。教师一方面要熟悉儿童的思维，另一方面不能丢失自己原有的深层思维，要做到在儿童的认知世界与理性的数学世界之间自由行走。这也是防止教师思维被“童化”的有效措施。

3. 要熟知学科大循环体系，形成整体认识

长期在低年级任教的教师，解答高年级的数学题时，常常会感觉思路不畅，常常有“越教越笨”的感觉，感觉自己学科性的主体知识在“退化”。“只有当教师的知识视野比学校教学大纲宽广得无可比拟的时候，教师才能成为教育过程的真正的能手、艺术家和诗人。”如果教师只能应付当天要教的一段教材，学生怎么能对数学产生浓厚兴趣？数学教师应该对全套教材知识的来龙去脉做到了然于心，达成对数学知识的深度体会和整体把握。每一位教师心中一定要有整个小学数学阶段知识的脉络和知识的发展图谱。此外，教师还要熟悉中学的数学知识，了解高等数学的知识和前沿知识。教师要站在整体的角度，包括知识技能層面、思想方法层面乃至理性精神层面，让数学知识联系贯通起来。

4. 要形成结构化的认知，提升数学素养

在学生学习过程中，越是概括化、结构化的内容，越有利于他们进行迁移，越容易转化为他们的能力。只有教师先形成结构化的认知，才可能有效地帮助学生进行结构化认知。因此，教师要探求整个小学阶段数学知识之间的联系，形成认识上的整体概念，将每一节课、每一单元，甚至是每一册碎片化的知识素材加以归纳和整理，穿珠成链，聚零为整，使之条理化、整体化。教师还要注重呈现方法之间本质和内在的关联，打通路径，实现结构化认识。在平时每一天的教学中，要以结构化的形式呈现学习内容，引领学生探寻问题在原有知识结构中的位置，促进学生深度思考、深度建构、深度学习。教师要为学生创设综合运用所学知识、方法、策略的情境，通过综合应用，让知识、方法、策略融合生长，让学生在运用的过程中重新发现与构建，运用各种策略，感受各种数学思想，体会数学的应用价值。

此外，不少年轻教师对课堂教学的理解主要来自书本，多停留在理论层面。教师要在不断实践中对教学做出理性反思，将所学的理论知识与教学实践真正结合起来，才能对今后的课堂教学做出更有针对性的指导，从而切实提升学生的核心素养，为学生后续的发展做好准备。