基于外环速度补偿的封闭机器人确定学习控制

王 敏 林梓欣 王 聪 杨辰光

近年来,机器人在工程应用和日常生活中发挥着越来越重要的作用,被广泛应用于空间探测、焊接、装配、医疗等领域,相关技术也越来越受到科研人员重视[1-3].在机器人控制领域,其控制目标之一就是实现机器人对特定任务轨迹的跟踪.多自由度机器人作为一个高度耦合的非线性多输入多输出系统[4],主要控制难点在于机器人工作环境任务多变,在外界扰动、负载变化、参数测量不精确等因素影响下,机器人系统精确建模难度较大,使得比例积分微分(Proportional-integral-derivative,PID)控制等经典控制算法难以满足机器人控制的精度要求.针对机器人系统存在部分参数不确定或测量不准确的问题,一些学者结合鲁棒控制、滑模控制等思想,提出了许多有效的自适应控制算法[5-7].当机器人系统存在不可建模动态时,一些学者结合神经网络的非线性函数逼近特性,提出了大量的自适应神经网络控制方案,保证了机器人在多变环境下的高性能控制[8-12].

值得注意的是,上述控制方案大多数都是基于力矩进行控制器设计,其方案有效性主要是通过数值系统仿真进行验证,鲜有在实际机器人上进行实验和应用.造成上述现象的原因是,当前市面上大部分工业/商业机器人并不开放力矩接口,而是采用速度/位置控制.这些封闭机器人采用标准的内外环控制结构,其中外环为运动学环,内环为动力学环,内环控制的采样速率一般比外环要快得多,且普遍认为其内环控制使用速度比例积分(Proportional-integral,PI)控制器或位置PID 控制器[13].封闭机器人的这些性质,导致用户一般只能对其进行简单的运动学控制[14],从而使得机器人难以应对多变的个性化产品加工.针对这类具有内外环结构的机器人的控制问题,部分学者提出了解决方案.文献[5,15]在研究具有未知动力学和未知运动学的机械臂控制时,提出了适当的自适应控制器.文献[16]研究了一类具有关节速度反馈内环的机器人任务空间控制问题,提出了一种基于模型的内环关节速度控制器通用结构[17].注意到,上述控制方案中跟踪误差的收敛依赖于内环速度控制器的修改或再设计,并不是常见的速度PI 控制器或位置PID 控制器,对于具有不可修改内环的工业/商业机器人而言,这些控制方案也难以实现应用.进一步,一些学者提出了预校正方案[18],这些预校正方案的有效性验证主要是通过直观解释和实验结果进行的,并没有进行严格理论分析.针对封闭机器人控制存在的上述问题,文献[19]在考虑机器人具有可以线性参数化的未知动力学和运动学且内环控制器参数未知和不可修改的背景下,设计了一类外环自适应速度补偿控制器,保证了机器人系统的稳定性和误差收敛.该方案需要计算动力学和运动学回归矩阵,这两个矩阵随着机械臂关节增多,计算的复杂度呈指数倍增长.此外,实际机器人系统由于受到阻尼以及摩擦力等影响,存在本质的非线性.因此,如何提出简单有效的封闭机器人控制方案,既能实现封闭力矩的补偿控制,又能精确建模未知非线性仍是一个开放性的问题.

众所周知,神经网络是建模未知非线性的有效方法[20].然而,现有的大部分自适应神经网络控制并没有充分利用神经网络的学习能力,即使是处理相同的任务也需要对神经网络进行重复训练,该过程耗时长、计算资源消耗大、暂态阶段的控制性能也较差.因此,如何实现神经网络在控制过程中的学习和经验知识再利用是一个很有意义的课题[21].对此,文献[22]提出确定学习理论,解决了神经网络对未知动态的学习问题.该理论证明了沿着回归轨迹的径向基函数(Radial basis function,RBF)神经网络满足持续激励(Persistent excitation,PE)条件,进一步结合线性时变系统指数稳定性证明了神经网络权值的精确收敛.基于该理论,文献[23]引入动态面技术,解决了自适应神经网络在严格反馈系统中的学习问题.近年来,确定学习理论也已被广泛应用于机器人编队控制[24]、心肌缺血早期诊断[25]、水面无人船控制[26]等领域,在机械臂控制领域也有相关工作[27].然而,现有基于确定学习的控制方案仍是基于力矩进行设计的,无法在封闭的工业/商业机器人上直接进行应用.

综上所述,本文针对未开放力矩接口的一类封闭机器人系统,在考虑机器人受到未知动力学影响且具有未知内环PI 速度控制器的情况下,基于文献[19]的外环补偿框架提出了一种基于外环速度补偿的确定学习控制方案,实现了封闭机器人的关节轨迹跟踪控制.该方案的主要贡献点如下: 1)在文献[19]的工作基础上,引入神经网络处理系统未知动态,取消了封闭机器人未知动力学模型参数线性化假设,并简化了外环补偿控制设计过程;2)采用宽度RBF 神经网络动态增量神经网络节点,降低了网络结构复杂度,改善了系统控制的实时性;3)引入确定学习理论,实现了宽度RBF 神经网络对封闭机器人未知动态的精确学习,并利用经验知识避免了对网络重复训练,降低了计算负担,实现了快稳准的高精度跟踪控制;4)为确定学习理论应用于具有类似结构的封闭机械系统提供了研究思路,拓展了确定学习的应用范围.

1 问题描述及预备知识

1.1 系统说明与控制目标

本文所考虑的由永磁直流电动机驱动的n自由度机器人动力学模型[19]如下

其中,x1∈Rn是机器人关节角位置;M(x1)∈Rn×n是机器人的惯性矩阵;C(x1,)∈Rn×n是机器人的科氏力矩阵;G(x1)∈Rn是机器人的重力向量;K ∈Rn×n是机器人内部的控制增益,为一常值对角正定矩阵;u∈Rn是封闭机器人的内环控制器.

性质 1.机器人动力学方程的惯性矩阵M(x1)是对称并一致正定的,且具有一致的界限,存在正常数λm和λM使得λmI ≤M(x1)≤λMI,其中I为适当定义的单位矩阵.

性质 2.可以通过适当定义机器人动力学方程的科氏力矩阵C(x1,),使得(x1)-2C(x1,)是斜对称矩阵.

在研究的封闭机器人内外环控制方法中,本文考虑内环控制器为PI 速度控制器[19],结构如下

考虑如下光滑有界参考模型,该模型将产生封闭机器人的关节期望轨迹

其中,xd1∈Rn和xd2∈Rn分别是封闭机器人期望的关节角位置和角速度,f(xd1,xd2)是给定的光滑非线性函数,yd=xd1是封闭机器人期望输出.本文假设期望输出yd为周期轨迹.

本文的控制目标是基于外环速度补偿控制思想,在考虑封闭机器人具有不确定动力学和未知参数内环控制器的情况下设计系统(1)的速度控制指令,从而确保: 1)机器人系统的所有信号都是最终一致有界的;2)系统的输出x1能够跟踪给定的期望输出轨迹yd;3)在控制过程中学习机器人内部未知动态,并利用学到的未知动态知识实现封闭机器人高精度跟踪控制.控制方案框图如图1 所示.

图1 封闭机器人控制系统框图Fig.1 Schematic diagram of manipulators with closed architecture control system

1.2 RBF 神经网络

1)RBF 神经网络的万能逼近特性: 为逼近机械臂控制过程中的未知非线性动态,本文使用如下形式的RBF 神经网络

那么向量函数S满足PE 条件,其中I定义为s×s维的单位矩阵.

引理 1[22]. RBF神经网络的局部PE条件: 考虑任意回归/周期轨迹Z,假设Z是从[0,∞)到Rq的连续映射,且Z位于紧集 ΩZ ⊂Rq中.则对于中心置于规则晶格(足够大到覆盖紧集 ΩZ)上的RBF神经网络,只有中心位于回归/周期轨迹Z的小邻域内的神经元才会被激励,由其组成的回归子向量Sζ(Z)将满足PE 条件.

1.3 宽度RBF 神经网络

在传统的RBF 神经网络逼近中,需通过选取合适的神经元节点数、中心和宽度来保证逼近精度,而在实际应用中通常需要设计者根据自己的经验不断试错,采用均匀布点的方式来设计RBF 神经网络的结构,具有很强的主观性.同时,机器人控制系统是一个多输入多输出系统,随着控制连杆数量的增加,RBF 神经网络的输入维数会呈几何倍数增长,在均匀布点的设计方案下,神经元数量也会急剧升高,这将导致神经网络的计算负荷提高,对硬件设备提出了更高的要求,同时也将影响系统控制的实时性.为了解决上述问题,本文将使用文献[29]所提出的宽度RBF 神经网络方法进行网络结构设计.该方法结合宽度神经网络增量节点的思想,可实现在系统控制过程中神经元的自适应调整.

宽度RBF 神经网络在初始化阶段以系统的初始状态为第一个神经元,之后会根据神经网络的实际输入与网络已有神经元中心的距离来判断是否应该新增神经元.新增神经元的增加策略如下:

1)定义新增神经元所需参数

其中,ξn,ηn,Wn分别是新增神经元的中心、宽度和权值,本文新增神经元的宽度设置与已有神经元一致,权值统一初始化为零.

2)判断当前网络输入是否超出现有神经元所构成的紧集域

首先,本文使用欧氏距离来描述当前网络输入与神经元中心点的距离,根据距离选取离当前输入最近的k个点集Cmin={c1,···,ck},则可由下式获得新增神经元的中心

然后,设置判断是否新增神经元的可调阈值ε,当神经网络当前输入Z与神经元集合Cmin的平均中心位置之间距离大于阈值ε时,添加新的神经元,否则保持原有神经元集合不变.

2 外环自适应神经网络速度控制指令设计

本节将针对系统(1),采用反步法进行基于外环补偿的速度控制指令设计.首先将封闭机器人系统的内环速度PI 控制器(2)代入系统(1),将系统(1)转化为如下形式

其中,KP=KKp,KI=KKi,y是机器人系统输出关节角位置,y=x1.

根据传统反步法设计思想,定义如下误差变量

其中,α1是虚拟控制器.考虑系统(8),接下来的反步设计包括两个步骤,将依次设计出虚拟控制器α1和速度控制指令.具体设计过程如下:

步骤 1.考虑系统(8)以及误差定义(9),对z1求导得

根据式(10),虚拟控制器α1可设计为

其中,c1为控制增益,且为正的设计参数.

步骤 2.根据误差定义(9),对z2求导可得

考虑封闭机器人系统具有未知的动力学和内环速度PI 控制器,定义未知系统动态为

其中,c2是速度控制指令q˙c的控制增益,且为正的可设计参数;γ,σ分别是神经网络权值估计值更新率的控制增益和σ修正项,均为正的待设计参数.

注 1.在考虑未知动力学影响的机器人自适应神经网络控制器设计中,现有大部分成果均为力矩控制器,无法应用于本文所考虑的封闭机器人系统.本文在机器人具有未知不可修改内环速度PI 控制器的背景下,设计了与内环相匹配的外环自适应神经网络速度控制指令.该指令与常见力矩控制器的代数方程形式不同,是一个关于qc的一阶微分方程,通过求解该微分方程,可以获得输入机器人系统的速度控制指令q˙c和位置控制指令qc,同时,RBF 神经网络的应用使该速度控制指令具有适应机器人未知动力学影响和未知内环控制器的能力.

注 2.与现有基于反步法的自适应神经网络力矩控制器相比,本文所设计速度控制指令在神经网络输入上将多出一个信号qc.这是因为在控制器设计过程中,为了处理内环速度PI 控制器的未知参数K,Kp,Ki带来的不确定性,本文在定义未知系统动态的时候将考虑在内,从而有助于后续的控制器设计以及未知动态的精确神经网络逼近.

至此,可得封闭机器人的闭环系统动态如下

定理 1.考虑由封闭机器人系统(8)、参考模型(3)、自适应神经网络速度控制指令(16)和神经网络权值估计值更新率(17)所组成的闭环系统,那么对于任意给定的常数µ>0 以及所有满足V(0)≤µ的系统初始状态,则通过选取合适的设计参数c1,c2,γ和σ,可以使得闭环系统中的所有信号是最终一致有界的,并且跟踪误差z1,z2能够收敛到零的小邻域内.

证明.选取如下Lyapunov 函数

结合机器人动力学方程性质2,沿系统(18)所产生的轨迹对所选Lyapunov 函数求导可得

利用Young 不等式对Lyapunov 函数的导数放缩得

其中,λmin(KP)是矩阵KP的最小特征值.

结合式(19)和式(21)可得

至此,只要选择a>b/µ,那么可以保证当V=µ时,≤0,因此V ≤µ是一个不变集,即对于任意满足V(0)≤µ的初始条件,对于任意t>0,有V(t)≤µ.进一步,对式(22)积分可得

从上式可知,通过选取合适的设计参数c1,c2,γ,σ,可使得θ任意小.因此,闭环系统中的所有信号是最终一致有界的.

进一步,从式(19)及式(23)可得

从上述分析可知,选取合适的设计参数可使θ任意小,即ν1,ν2可以任意小,因此跟踪误差z1,z2可以在有限时间T1内收敛到零的小邻域内.

3 基于确定学习的速度补偿控制

在第 2 节,本文针对封闭机器人系统(8)设计了外环自适应神经网络速度控制指令(16)以及神经网络权值估计值更新率(17),并证明了系统在该控制指令的作用下是最终一致有界的,且系统跟踪误差可在有限时间T1内收敛于零的小邻域内.本节将基于确定学习理论[22],进一步验证神经网络对封闭机器人系统(8)未知动态的准确学习,且实现学习后的常值神经网络权值的表达与存储.

其中,ϵ1(Z1)是神经网络对未知系统动态的逼近误差,且‖ϵ1(Z1)‖≤ϵ∗,ϵ∗是一个任意小的正整数,且常值神经网络权值的表达式为

其中,tb >ta >T1,[ta,tb] 是系统达到稳态后的一段时间.

证明.证明分为以下两个部分进行:

1)神经网络输入Z1回归性证明.

定理 3.考虑由封闭机器人系统(8)、参考模型(3)、基于确定学习的速度控制指令(31)所组成的闭环系统,对于任意给定的常数ρ>0 以及所有满足U(0)≤ρ的系统初始状态,则通过选取合适的待设计参数c1,c2可使得闭环系统中的所有信号是最终一致有界的,并且跟踪误差z1能够收敛到零的小邻域内.

该证明与定理1 的证明过程类似,此处略.

注 3.基于自适应神经网络的速度补偿控制方案需要在线自适应调整神经网络估计权值,主要适用于控制任务变化的工作场景.基于确定学习的速度补偿控制方案包括两个工作阶段: 神经网络训练和经验利用.神经网络训练阶段,即自适应调节过程,该阶段适用任务多变的工作场景;经验利用阶段,即利用训练阶段获取的未知动态知识构造神经网络学习控制器,提升系统的暂态控制性能和降低在线计算量,主要适用于与训练阶段控制任务相同或相似的工作场景.

4 实验验证

为验证本文所提方案的有效性,本节将分别在双连杆封闭机器人数值系统和实际UR5 机器人平台上进行实验验证.UR5 机器人作为市面上常见的工业机器人,其力矩控制接口不予开放,一般只可做运动控制,符合本文封闭机器人的研究背景.

4.1 数值仿真

本节将对定理1 所提自适应控制方案以及定理3 所提学习控制方案进行对比实验,以验证RBF神经网络在稳定自适应控制过程中的学习和知识再利用能力,并分别使用均匀布点和宽度RBF 神经网络两种网络构造方式完成上述对比实验,以验证宽度RBF 神经网络的优越性.考虑由(1)和(2)组成的双连杆封闭机器人动力学模型

其中,x1=[x1,1,x1,2]T,x1,1和x1,2分别代表封闭机器人的关节1 角位置和关节2 角位置,且各矩阵为

宽度RBF 神经网络方案下的仿真结果如图2～图5 所示.图2～图4 展示了封闭机器人系统在自适应控制阶段的控制效果,从图2 可以看出机器人的关节输出均很好地跟踪上了给定的期望轨迹,图3表示RBF 神经网络的权值在一段控制时间后实现了收敛,图4 表示RBF 神经网络成功逼近未知动态,验证了网络的学习能力.图5 展示了封闭机器人系统在不同控制方案下的控制效果.由图可知,在仅依靠内环PI 控制的情况下,系统跟踪误差较大,外环补偿控制的引入大幅度提高了系统跟踪精度.进一步,学习控制阶段的控制效果与自适应阶段的控制效果相比,暂态阶段超调量更小,且暂态时间也更短,在7 s 左右跟踪误差就收敛到零附近,比自适应控制减少了约84%.

图2 封闭机器人关节角位置跟踪效果(自适应控制)Fig.2 Angular-position tracking performances of two joints for the manipulator with closed architecture(Adaptive control)

图3 神经网络权值范数Fig.3 The norm of neural network weights

图4 神经网络对未知动态 f (Z1)学习效果(自适应控制)Fig.4 Neural network＇s learning performance of unknown dynamics f (Z1)(Adaptive control)

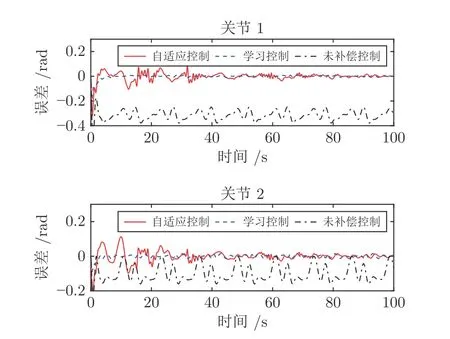
图5 封闭机器人关节角位置跟踪误差(控制方案对比)Fig.5 Angular-position tracking errors of two joints for the manipulator with closed architecture (Comparison of different control methods)

此外,本节在神经网络节点的均匀布点和动态布点下,进行了控制方案的性能对比实验研究.在实验中,均匀布点方案下控制器参数设置如下:c1=0.9,c2=0.8,γ=0.4,σ=0.00012,选取含有6561个神经元的RBF 神经网络.对比实验结果见表1.表1 中,ANC 表示自适应神经网络控制,LC 表示学习控制.从表1 数据可知,宽度RBF 神经网络的使用有效降低了神经元的数量,进而大幅减小神经网络计算负荷,因此使用宽度网络的控制方案在仿真时长上远远小于使用均匀布点的控制方案,从平均绝对误差(Mean absolute error,MAE)可知,宽度网络的使用基本实现了机器人对期望轨迹的有效跟踪,但跟踪效果稍差于均匀布点的控制方案.

表1 仿真结果对比Table 1 Comparison of simulation results

4.2 实物实验

为进一步验证所提方案的有效性,本节将在UR5 机器人上进行实验,取机械臂第2、3 关节为控制对象.UR5 机器人由机器人本体、控制箱、示教器和计算机组成.计算机运行Matlab 程序实时计算速度控制指令,并通过有线网络将指令传输给机器人控制箱以及获取所需机器人状态.实验所选期望轨迹为yd=[0.5 sin(0.5t),0.5 sin(0.5t)]T,系统初始状态为x1=[0,0]T,x˙1=[0,0]T,仿真步长为40 ms.自适应控制阶段时长为400 s,学习控制阶段时长为100 s.控制器参数设置如下: 初始神经元设置为[0,0,0,0,0.5,0.5,0.2,0.2],c1=1.8,c2=0.4,γ=0.12,σ=0.002,ε=0.15,β=0.95,神经元宽度为[0.3,0.3,0.3,0.3,0.3,0.3,0.3,0.3].

图6 展示了UR5 机器人运动过程中不同时间下的运动状态,实验结果如图7～图9 所示.图7、图8 展示了机器人在自适应阶段的控制效果.在图7中,本文根据图6 标定了机器人在对应时刻下的关节角位置.结合图6 和图7 可知,UR5 机器人的关节角很好地跟踪上了给定的期望轨迹,从图8 可知,神经网络权值在有限时间内成功收敛.图9 展示了机械臂在学习控制阶段的控制效果,图9 中结果与数值仿真的结果一致,通过神经网络对知识的再利用,学习控制阶段的跟踪误差更快地收敛,暂态时间更短,暂态误差也更小.

图6 UR5 机器人不同时间运动位置Fig.6 Positions of UR5 at different times

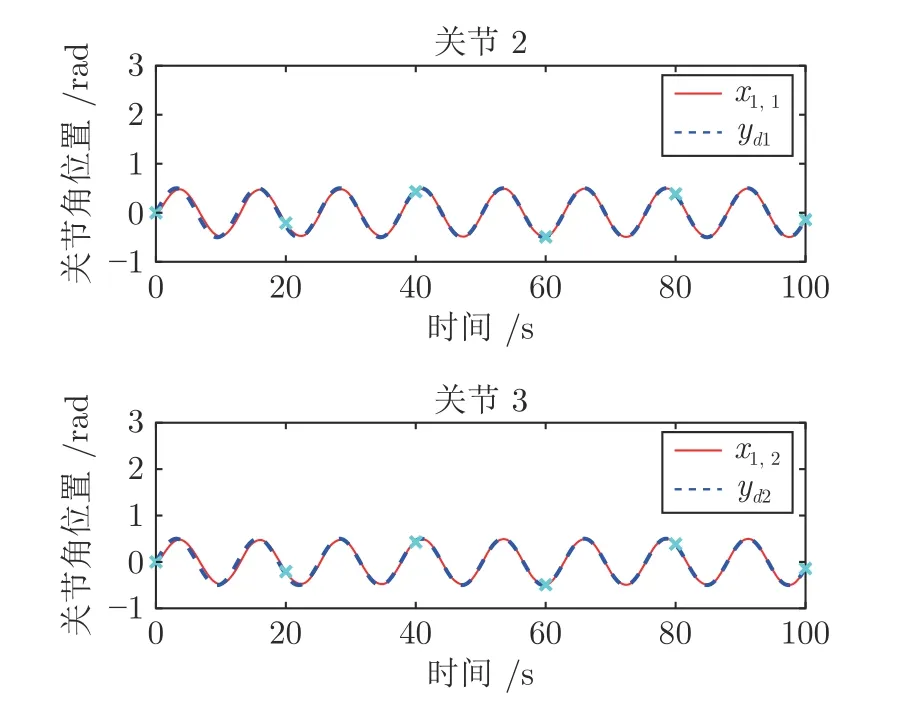
图7 UR5 机器人关节角位置跟踪效果(自适应控制)Fig.7 Angular-position tracking performance of UR5(Adaptive control)

图8 神经网络权值范数Fig.8 The norm of neural network weights

图9 UR5 机器人关节角位置跟踪误差(学习控制对比)Fig.9 Angular-position tracking errors of UR5(Compared to learning control)

5 总结与展望

本文针对未开放力矩控制接口的封闭机器人系统,提出了一种基于外环补偿的自适应神经网络速度控制方案.与现有大部分自适应神经网络控制方案不同的是,本文所提方案的控制输入为关节角速度而不是关节力矩,实现了自适应神经网络控制算法在封闭机器人上的应用,并通过引入确定学习机制,充分发挥神经网络的学习能力,提高了机器人在执行相同或相似任务时的控制性能.此外,利用宽度神经网络的动态网络布点方式,大幅降低了RBF 神经网络结构的复杂度,减小了设备计算负荷,提高了系统控制实时性.本文所提控制方案针对的是机器人关节空间控制,在未来的工作中,将逐步将其拓展到机器人任务空间控制、阻抗控制等,提高该控制方案的工程应用价值.