具有类万有引力的有界置信观点动力学分析与应用

刘青松 习晓苗 柴 利

在过去的几十年中,随着多智能体系统的兴起[1-3],社会网络引起了学者们的广泛关注,涌现了许多研究成果[4].例如,Ghaderi 等[5]研究了具有固执个体的社会网络观点的收敛性,给出了观点收敛时间的上界和下界.Xia 等[6]分析了具有偏见同化的非线性观点动力学模型的稳定性.Liu 等[7]提出一种观点扩散模型,描述了双层连通网络的观点扩散过程,探讨了在所有持有相同观点的耦合主体下,两种观点在三种类型的两层互连网络中的传播.针对强连通的社会网络,Ye 等[8]研究了表达观点和私人观点之间的差异,且给出了网络上保证意见指数快速收敛到极限的一般条件.针对拟强连通社会网络,刘青松等[9]研究了多维观点动力学行为,给出了表达和私人观点收敛的充分条件.Hou 等[10]分析了具有有界置信的表达观点和私人观点动力学行为,给出了最终聚类数主要由封闭个体率决定的结论.

近年来,学者们针对多自主体系统进行研究[11-14],提出了一些经典观点动力学模型,促进了社会网络中观点动力学的深入研究.20 世纪50 年代,社会心理学家French[15]提出基于个体的观点形成模型.1974 年,DeGroot[16]提出基于个体加权平均的观点动力学模型,即后来的DeGroot 模型.通过针对每个个体引入偏差,将DeGroot 模型推广到非线性观点动力学模型[6].另一方面,通过引入个体对自身初始观点的固执,文献[17] 提出Friedkin-Johnsen模型.之后,Parsegov 等[18]将Friedkin-Johnsen 模型推广到了多维观点动力学模型.Tian 等[19]研究了问题序列上的Friedkin-Johnsen 观点动力学模型,给出了问题序列上观点达到一致的充要条件.在考虑每次观点更新过程中,随机选取一对个体进行观点交流,Deffuant 等[20]提出Deffuant-Weisbuch 模型.随后,通过两种不同的方法推广了Deffuant-Weisbuch 模型[21],验证了观点几乎必然达到一致.最近,Dong 等[22]研究了基于领导概念的观点动态共识构建过程,Mei 等[23]提出基于评价网络的学习过程模型.

上述观点动力学模型是线性模型,经典的Hegselmann-Krause 模型[24]是非线性模型,描述了每个个体只与其置信阈值内的邻居进行观点交互.与Deffuant-Weisbuch 模型[20]相比,Hegselmann-Krause模型每次进行观点交流的个体的数量更多,因而交流效率更高,观点能够更快地收敛或者达成一致.在实际应用方面,Hegselmann-Krause 观点动力学模型可应用于机器人平面、空间交会问题[25]和社会心理学中“权威效应”[26]等方面的研究.故研究Hegselmann-Krause 或有界置信观点动力学模型,具有重要应用价值和意义.

近年来,国内外学者针对有界置信模型进行了较为深入的研究[27],例如Canuto 等[28]通过欧拉方法,研究了基于有界置信模型的动态系统的一致性问题.通过考虑噪声环境,Su 等[29]提出了具有噪声的有界置信模型,展示了随机噪声如何显著地影响同步的观点,给出了观点达成拟一致的充分条件.基于改进的有界置信模型,针对初始观点分布,Yang等[30]给出了观点收敛到一个聚类的充分条件.通过正规化交流权重的凸性和Gronwall-Halanay 型不等式,Haskovec[31]研究了具有时滞的有界置信模型的渐近一致性问题.基于离散异构的有界置信模型,Vasca 等[32]提出了一种基于非影响相似度区间的个体置信阈值自适应策略,分析了有限时间的观点动力学行为.

鉴于上述对有界置信观点动力学模型国内外研究现状的分析,目前主要存在以下三个问题: 1)在改进的观点动力学模型中,邻居对个体的影响力与其观点差异值成正比,与实际情景存在一定的差距[28];2)现有文献主要是采用仿真方法研究改进的有界置信模型,缺乏较为完整的理论研究框架[27];3)现有的有界置信模型研究中,较少研究观点动力学模型的应用[32],例如考虑建立的观点动力学模型在社会心理学中的应用.此外,根据社会心理学中的认知理论可知[33],由于不同个体社会背景和认知能力不一样,不同邻居对个体产生的影响就会不一样[33];个体与邻居的观点差异值越大,邻居对其影响应该越小[34].

为了克服上述问题,本文提出具有类万有引力的有界置信模型,并分析了观点的演化问题.本文的主要贡献如下:

1)提出了新的具有类万有引力的有界置信观点动力学模型.解决了Canuto 等[28]模型中个体的影响力与其观点差异值成正比这一不符合实际情景的社会现象,并考虑了个体的权威性;

2)在理论上给出了观点收敛的充分条件且分析了基于衰减置信阈值的观点动力学模型,完善了Chen 等[27]的理论研究内容;

3)应用本文提出的具有类万有引力的有界置信观点动力学模型,研究了社会心理学中的“权威效应”和“非零和效应”[35],填补了Vasca 等[32]缺乏的应用研究;

4)得到了邻居的权威性和正态分布的初始观点都有利于观点达成一致,这一重要结论.

1 问题描述

首先,回顾经典的有界置信观点动力学模型[24]:

式中,i∈V={1,2,···,n},xi(k)表示个体i的观点值.Ni=N(i,x(k))={j ∈V||xj(k)-xi(k)|≤ε}表示个体i所有邻居的集合,|Ni|表示个体i的邻居数目,其中ε为置信度阈值.

式中,社会影响权重wij(k)为:

由于社会影响权重wij(k)中:

是受万有引力表达式的启发[27],故称观点动力学模型(2)为具有类万有引力的有界置信观点动力学模型.

众所周知,万有引力的大小与物体的质量以及两个物体之间的距离有关.物体的质量越大,它们之间的万有引力就越大;物体之间的距离越远,它们之间的万有引力越小.根据社会心理学中的认知理论可知[33],个体权威性或者社会话语权越大,其影响力(权重)越大;个体与邻居的观点差异值越大,邻居对其影响应该越小[34].根据上述关系,将万有引力与影响力对应,物体的质量与个体权威性对应,物体之间的距离与观点差异值对应.另一方面,类似于经典的Hegselmann-Krause 模型,保证权重在[0,1]之间,故引入 tanh(·)函数给予保证.综上所述,便可得到权重式(4).此外,在本文的第4 节中,应用所提出的观点动力学模型研究社会心理学中的“权威效应”和“非零和效应”.从应用结果可进一步地说明权重式(4)的合理性.

事实上,dij描述了个体j与个体i观点值越接近,彼此间的影响也就越大.此外,|Nj|描述了个体i的邻居j的权威性或者社会话语权[27].从而本文提出的模型也很好地描述了,在一个社会中,拥有大量人脉资源的人享有更多的话语权,对他人的社会影响也就更大.注意到,如果dij=1,则具有类万有引力的有界置信观点动力学模型(2)退化成经典Hegselmann-Krause 模型(1).事实上,dij(k)是一个关于个体j邻居的个数N(j,x(k))和个体i与个体j观点值之差xj(k)-xi(k)的函数.易知个体j的邻居数越多,与个体i的观点值相差越小,则其对个体i的差异影响权重越大,其函数关系见图1.

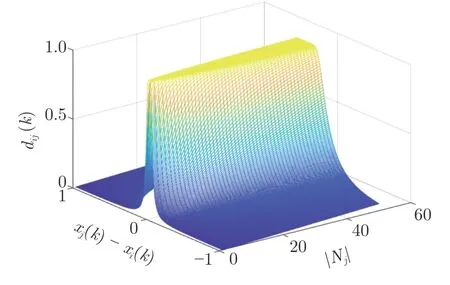
图1 dij(k)关于 |Nj|和 xj(k)-xi(k)的函数图Fig.1 The trajectories of dij(k)with respect to |Nj|and xj(k)-xi(k)

根据本文提出的具有类万有引力的有界置信观点动力学模型(2)可知,个体j对个体i的影响由wij(k)(xj(k)-xi(k))所决定,其函数关系见图2.由图2 可知,当xj(k)-xi(k)一定时,个体j的邻居数N(j,x(k))越多,其对个体i的影响越大.当个体j的邻居数N(j,x(k))一定时,个体j与个体i的观点值之差xj(k)-xi(k)越大,个体i的观点值受到个体j的影响先增大后减小.因此,要想某个体能对指定个体施加更大的影响,需要折中进行考虑.

图2 个体 j 对个体 i 观点的影响Fig.2 The influence of individual j on the opinion of individual i

本文主要研究具有类万有引力的有界置信模型(2)的观点演化问题,给出了观点收敛的充分条件,并将所提出的观点动力学模型应用到社会心理学中的“权威效应”和“非零和效应”.

2 收敛性分析

本节将分析具有类万有引力的有界置信观点动力学模型(2)的收敛性.

定义 1.在观点动力学模型(2)中,对任意个体i ∈V的初始观点值xi(0),如果存在R,使得:

则称模型(2)收敛.特别地,如果存在定常数α∈R,使得:

则称观点达成一致.

定理 1.对于任意观点初值xi(0)∈[0,1],i ∈V,观点动力学模型(2)收敛.

证明.模型(2)可重写为:

模型(5)可进一步写为:

式中,置信矩阵A(k,x(k))的元素aij(k)为:

即A(k,x(k))的对角线元素大于0.

另一方面,当个体j与个体i的观点值之差大于置信阈值时即j∈/Ni,则wij(k)=0.类似地,i∈/Nj,则wji(k)=0.因此,aij(k)=0 当且仅当aji(k)=0,∀i,j ∈V.此外,易知A(k,x(k))中一直存在正元素,即存在δ >0,使得A(k,x(k))的最小正元素大于δ.

综上所述,矩阵A(k,x(k))满足文献[36]给出模型收敛的充分条件,从而模型(6)收敛.故观点动力学模型(2)收敛.

根据定理1,可得下列推论.

推论 1.对于任意观点初值xi(0)∈[0,1],i ∈V,如果观点动力学模型(6)在经过kτ次演化后观点达成一致,则置信矩阵A(k,x(k))=(1/n)1n,k ≥kτ,其中1n=[1,1,···, 1]T.

证明.如果观点经过kτ次演化后达成一致,即|xi(k)-xj(k)|→0,∀i,j ∈V,k ≥kτ且Ni=Nj=n,则:

由式(3)可得:

进一步地,根据式(7)可知,aij=1/n,k ≥kτ.

为了得到进一步的结果,令:

推论 2.考虑观点动力学模型(2),对于任意观点初值xi(0)∈[0,1],i ∈V.如果置信阈值ε=1 且:

证明.由于置信阈值ε=1,则所有个体均可交流,即 |Ni|=n.由观点动力学模型(2)可知:

注意到,邻居j对个体i的影响为wij(k)(xj(k)-xi(k)),类似地,邻居i对个体j的影响为wji(k)(xi(k)-xj(k)),然而,wij(k)=wji(k).易得:(k)(xj(k)-xi(k))+wji(k)(xi(k)-xj(k))=0则式(9)可退化为:

第2 节主要考虑的是置信阈值不变的情况.事实上,观点动力学模型可看作一个谈判的过程模型.一方面,个体期望它的邻居在每一轮谈判中显著地向它的观点靠拢,以便继续谈判,衰减置信阈值可描述这一情景[37];另一方面,具有衰减置信阈值的观点动力学模型可应用于研究图中的社区检测[37]和社会心理学中的“非零和效应”.故第3 节将分析基于衰减置信阈值的观点动力学模型.此外,本文将利用建立的具有衰减置信阈值的Hegselmann-Krause 观点动力学模型研究社会心理学中的“非零和效应” (见第4.2 节).

3 衰减的置信阈值

为了描述个体在谈判的过程中,个体期望它的邻居在每一轮谈判中显著地向它的观点靠拢,以便继续谈判.本节考虑下列具有衰减置信阈值的观点动力学模型:

式中,R>0 和 0<ρ≤1.

定理 2.考虑观点动力学模型(10),对于任意观点初值xi(0)∈[0,1],i ∈V,观点xi(k),i ∈V是收敛的.进一步地,令xi∗表示个体i的最终观点值,对于所有的k∈V,则:

证明.根据式(10),有:

由式(12),可得:

令∀k,τ=0,1,···,则由式(14)可知:

因此:

式中,ρ∈(0,1).易知序列xi(k),k=0,1,···是一个Cauchy 序列,故其收敛.通过令式(15)中的τ→∞,则可得式(13).

类似于观点动力学模型(2),如果置信度阈值ε=1且式(11)退化为式(8).则观点动力学模型(10)具有和推论2 一样的结论.

4 观点动力学模型的应用

4.1 权威效应

本节将利用本文提出的具有类万有引力的有界置信观点动力学模型(2),研究普遍存在的社会心理学现象: 权威效应.所谓权威效应是指一个人要是地位高、有威信、受人敬重,那他所说的话及所做的事就容易引起别人重视,并让他们相信其正确性.权威效应的普遍存在,一方面是由于人们总认为权威人物往往是正确的楷模,服从他们会使自己具备安全感,增加不会出错的保险系数;另一方面,由于人们总认为权威人物的要求往往和社会规范相一致,按照权威人物的要求去做,会得到各方面的赞许和奖励.在现实生活中,有很多利用权威效应的例子,比如做广告时请权威人物赞誉某种产品,在辩论说理时引用权威人物的话作为论据等.在人际交往中,利用权威效应,能够引导或改变对方的观点和行为.

考虑由10 个个体组成的社会网络,设初始观点值为:

置信阈值ε=0.2.根据初始观点值和置信阈值可得初始时刻个体之间的网络结构,如图3 所示(图中自环未画出).易知个体4 具有8 个邻居即|N4|=8,具有最大的权威性或者话语权.

图3 网络拓扑结构 (个体4 为权威个体)Fig.3 Network structure (individual 4 is the authoritative individual)

当观点动力学模型(2)中wij为式(8)时,即不考虑邻居的权威性,其观点演化曲线如图4(a)所示,其中形成两簇的最终观点值分别为 0.51 和 0.21.当观点动力学模型(2)中wij为式(3)时,即考虑邻居的权威性,其观点演化曲线如图4(b)所示,其中形成两簇的最终观点值分别为 0.46 和 0.24.出现这一现象是由于受到了权威者个体4 的影响 (图4 中虚线为个体4 的观点曲线),两簇观点都向个体4 的观点值靠近.

图4 权威效应 (个体4 为权威个体)Fig.4 Authority effect (individual 4 is the authoritative individual)

为了说明初始条件的客观性,可随机选取一个个体为权威个体,不失一般性地,选取个体5 为权威个体,个体初始观点值可设为x(0)=[0.25,0.25,0.32,0.45,0.5,0.7,0.7,0.7,0.7,0.8]T,其网络拓扑图如图5 所示.易知,个体5 具有7 个邻居即 |N5|=7.类似地,其观点演化曲线如图6 所示,可以看出,由于受到权威个体5 的影响 (图6 中虚线为个体5 的观点曲线),两簇观点都向个体5 的观点值靠近.

图5 网络拓扑结构 (个体5 为权威个体)Fig.5 Network structure (individual 5 is the authoritative individual)

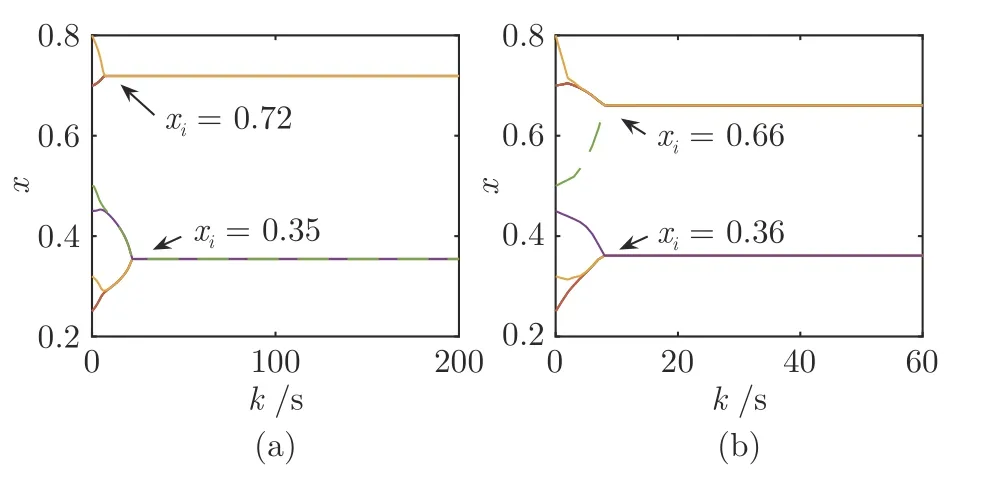
图6 权威效应 (个体5 为权威个体)Fig.6 Authority effect (individual 5 is the authoritative individual)

4.2 非零和效应

本节将利用本文建立的具有衰减置信阈值的观点动力学模型(10),研究社会心理学中“非零和效应”.“非零和效应”是一种合作下的博弈,博弈中做一定的让步,双方的收益或损失的总和不是零,观点达成一致,谈判便可成功[35].另一方面,衰减置信阈值可描述个体期望它的邻居在每一轮谈判中显著地向它的观点靠拢,以便继续谈判.

为了利用本文提出的模型(10)研究社会心理学中“非零和效应”,令R=0.8,ρ=0.7,当个体观点初值xi(0)∈[0,1],i ∈V均匀分布时,观点动力学模型(10)的仿真结果如图7(a)所示,观点达到了一致,说明谈判取得成功,实现了“非零和效应”.当个体观点初值x(0)∈[0,1]n正态分布时,其结果如图7(b)所示,观点达到一致性的速度比个体观点初值均匀分布情况快,说明谈判过程中,当持中立观点的人较多时,谈判取得成功的时间更少.

图7 非零和效应Fig.7 Sum non-zero effect

5 仿真分析

5.1 基于固定置信阈值的模型仿真分析

本节将通过仿真分析本文所得到的理论结果.设群体总个体数n=50,置信度阈值ε=0.3,观点初值xi(0)∈[0,1],i ∈V均匀分布.将改进的Hegselmann-Krause 观点动力学模型[32]与本文提出的观点动力学模型(2)进行对比,其观点演化曲线分别如图8(a)和图8(b)所示,可以看出,在改进的Hegselmann-Krause 模型[32]中,观点形成拟一致.有趣的是在具有类万有引力的有界置信模型(2)中,观点则出现两极分化.这是因为在文献[32]改进的Hegselmann-Krause 模型中,观点相似的个体不再进行交互,而本文提出的具有类万有引力的有界置信模型(2)中,考虑了影响权重的互异性.

图8 初值为均匀分布时的观点演化Fig.8 Opinion evolution when the initial value is uniformly distributed

当在具有类万有引力的有界置信模型(2)中不考虑个体权威性时即 |Nj|=1,其观点演化曲线如图8(c)所示,观点仍然达到两极分化,但其观点形成两极分化的速度比图8(b)的慢,说明权威个体有利观点的演化速度.

为了描述观点演化过程中所有观点的相对变化,定义变量:

其曲线如图8(d)所示.可以看出,在文献[32]改进的Hegselmann-Krause 模型中,观点相对变化较大,而在具有类万有引力的有界置信模型(2)中,观点相对变化较小;另一方面,在不考虑权威个体的模型(2)中,观点相对变化最小,但观点收敛速度最慢.特别地,如果η(k)=0,则群体观点收敛.

在现实生活中,针对一些(如不感兴趣的)话题,大多数人的观点比较趋于中立,而只有少部分人的观点比较极端.为此,设个体观点初值xi(0)∈[0,1],i ∈V为正态分布.将改进的Hegselmann-Krause 模型与本文建立的有界置信模型(2)进行比较,其观点曲线如图9(a)和图9(b)所示.可以看出,基于有界置信模型(2)的观点达到一致,而基于改进的Hegselmann-Krause 模型的观点不收敛,这是因为改进的Hegselmann-Krause 模型中,观点相似的个体不再进行交互.

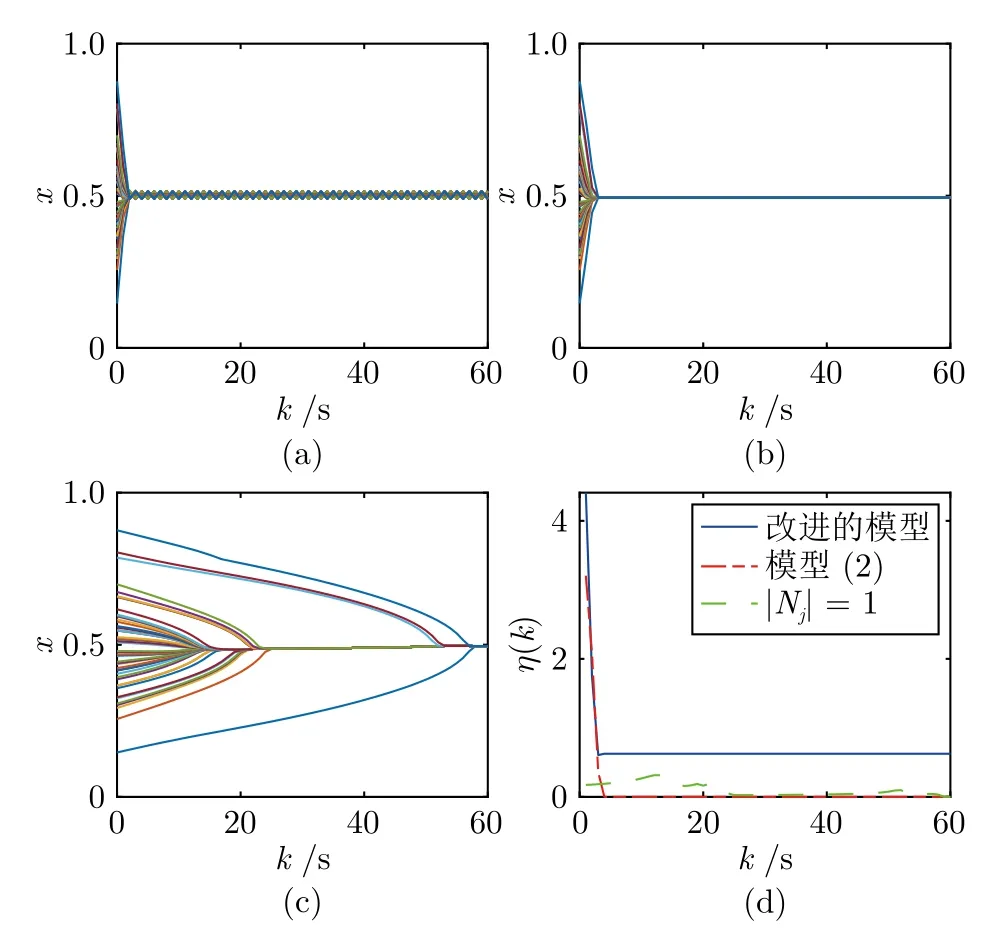
图9 初值为正态分布时的观点演化Fig.9 Opinion evolution when the initial value is normally distributed

当具有类万有引力的有界置信模型(2)不考虑个体权威性时即 |Nj|=1,其观点曲线如图9(c)所示,可以看出,基于观点动力学模型(2)的观点达到一致速度较慢.根据η(k)的定义和图9(d)可知,基于改进的Hegselmann-Krause 模型的观点相对变化最大.

5.2 基于衰减置信阈值的模型仿真分析

本节将对具有衰减置信阈值的观点动力学模型(10)进行仿真分析.设R=0.3,ρ=0.7 和n=50,当观点初值xi(0)∈[0,1],i ∈V均匀分布时,观点动力学模型(10)形成了3 个均匀的观点簇,仿真结果如图10(a)所示.当观点初值x(0)∈[0,1]n正态分布时,其结果如图10(b)所示,形成了4 个观点簇.总之,基于衰减置信阈值的模型(10)的观点都是收敛的.

图10 模型(10)观点演化Fig.10 Opinion evolution of model (10)

设Nc表示群体最终观点簇数,Nm表示群体最大观点簇中的个体数量.在个体数n和观点初值x(0)以及阈值参数R都固定的情况下,随着ρ的增大,群体最终观点簇数量Nc减少,如图10(c)所示.由图10(d)可知,群体最大观点簇中个体数量Nm随着ρ的增大而增大.特别地,当Nc=1 时,则群体观点达到一致性.

6 结束语

本文提出具有类万有引力的有界置信观点动力学模型,描述了不同邻居对个体的观点影响权重不一样,且个体观点的更新与观点之间的差值和邻居的权威性有关.根据置信矩阵的性质证明了观点的收敛性,在不考虑邻居权威性的条件下,给出了最终观点平均值的显式表达式.在衰减置信阈值的条件下,得到了观点收敛速率的显式解.利用本文提出的观点动力学模型,研究了社会心理学中的“权威效应”和“非零和效应”.仿真分析表明,邻居的权威性和正态分布的初始观点都有利于观点达成一致.