基于极值特征神经网络的气缸压力曲线降噪

梁金凤,王希波,马飞燕,杨 硕

(山东交通学院 汽车工程学院,山东 济南 250357)

0 引言

汽车发动机气缸压力作为发动机内燃过程的核心参数之一,对于发动机性能优化、控制和诊断等方面有着重要意义。通过测量发动机气缸压力可以衡量和分析内部燃烧过程[1-2],进而优化燃烧过程和提高燃烧效率。实时监测和处理气缸压力数据可以对发动机各个部件的工作状态进行分析判断,实现更加精确有效的控制输出。将一段时间内的气缸压力采样数据连续描绘形成曲线,可以更加直观地观测气缸压力的变化趋势,对曲线求取高阶导数能进一步分析发动机的工作状态和性能特征,如最大压力点、点火提前角、爆震等,通过分析这些特征点可以了解发动机的工作情况和潜在问题。气缸压力曲线的异常变化可能是发动机故障的信号之一,通过分析高阶导数可以定位异常振动和噪声的来源,进而采取相应的措施解决问题。高阶导数可以揭示气缸压力曲线中的燃烧特征,通过分析燃烧过程的气缸压力高阶导数可以对控制系统进行调整,优化点火时机、燃油喷射策略等控制参数,实现更高的功率密度、更低的排放、更高的燃油经济性等目标。

为了能得到更加平滑精确的曲线拟合结果,有关学者对于曲线拟合进行了深入的研究。在运用数据信号处理算法对曲线进行光顺处理方面上,宋俊芳等人基于端点一阶导矢连续法拟合出光顺曲线[3];王可等人提出基于拉格朗日乘数法的点云数据光顺处理方法,该方法在保持点云平滑性和连续性的同时降低了点云表面的不规则性或噪声[4];杨光等人通过融合多个算法提出了一种消除示功图曲线干扰信号的处理算法,该算法可以有效过滤数据中的高频干扰信号,获得光顺、失真较少的柴油机示功图曲线[5-6]。随着人工智能的发展,神经网络成为一种强大的非线性拟合工具,并被广泛地应用于曲线和曲面拟合问题中,它可以通过学习数据特征进行高精度的函数逼近和拟合。张东晓等人利用循环神经网络根据已有的部分测井曲线生成人工测井曲线[7];侯国鑫等人以神经网络作为工具对轴流泵运转特性进行曲线拟合[8]。

在求取汽车发动机气缸压力关于曲轴转角的高阶导数时,随着导数阶数的增加,可能会使噪声增加和干扰放大,使拟合结果的高阶导数偏离真实的物理趋势,因此需要对采样数据进行有效降噪[9]。本文提出基于极值特征神经网络对汽车发动机气缸压力特征曲线进行降噪拟合,考虑到气缸压力随曲轴转角的变化规律,将曲线形成过程中的极值点数目作为约束引入神经网络的损失函数中。

通过与浅层神经网络和样条拟合方法对比分析验证极值特征神经网络对于气缸压力曲线的降噪性能,并采用极值特征神经网络对另外6种工况的气缸压力数据进行降噪拟合以进一步分析其适用性。

1 极值特征神经网络

发动机气缸压力曲线随曲轴转角的变化具有一定的规律,其导函数的极值点数目相对稳定。通过多个循环平均可以得到满足发动机指示功、热效率计算的气缸压力曲线,但对发动机缸内热力过程进行高阶导数分析时,气缸压力曲线上的不规则噪声会使高阶导数的曲线偏离物理真实[10],采用极值特征神经网络可以对气缸压力曲线进行有效降噪,使得气缸压力高阶导数曲线偏离物理真实的程度降低。

1.1 极值特征神经网络的架构

构建由输入层、单隐藏层、输出层、自动微分层、极值特征层组成的极值特征神经网络,如图1所示。输入层和输出层的节点数目都为1个,单隐藏层的节点数目为9个[11]。自动微分层的作用是计算输出对于输入的高阶导数。极值特征层的主要作用是得出气缸压力曲线极值点数目。损失函数由样本计算误差LossP和极值特征误差LossE两部分加权和组成,样本计算误差LossP是网络进行学习时预测值与真实值之间的差距,极值特征误差LossE是网络计算得到的极值点数目与真实物理过程的极值点数目之差。根据损失函数对神经网络进行迭代训练,直到神经网络的权值和偏置值使得极值特征误差和样本误差满足要求。激活函数选择sigmoid函数。极值特征神经网络的输出表示为式(1):

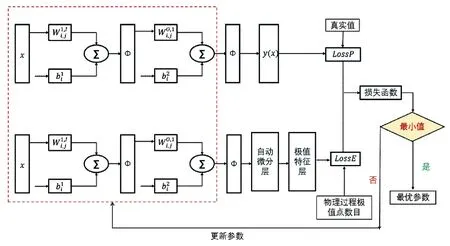
图1 极值特征神经网络结构示意图

(1)

1.2 递归公式

气缸压力曲线的分析模型中压力关于曲轴转角的导数最高阶数为2阶,在对气缸压力曲线的降噪结果进行分析时只需用到4阶导数即可满足要求,因此极值特征神经网络中的导数的最高阶导数取到4阶即可,sigmoid激活函数如式(2)所示,sigmoid激活函数前4阶导数用导数链式法则求得如式(3～6)所示。

(2)

f′(x)=-[f(x)]2+f(x)

(3)

f″(x)=2·[f(x)]3-3[f(x)]2+f(x)

(4)

f(3)(x)=-6·[f(x)]4+12·[f(x)]3-7·[f(x)]2+f(x)

(5)

f(4)(x)=24·[f(x)]5-60·[f(x)]4+50·[f(x)]3-15·[f(x)]2+f(x)

(6)

根据法迪·布鲁诺公式可以得到极值特征神经网络自动微分层输出关于输入的1～4阶导数,如式(7～10)所示:

(7)

(8)

(9)

(10)

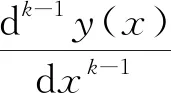
(11)

1.3 损失函数

极值特征神经网络的损失函数由样本计算误差LossP和极值特征误差LossE加权和得到。样本计算误差LossP由网络的输出的预测值和样本真实值的差得到,极值特征误差LossE的计算来源于真实物理过程的认知,以真实物理过程的极值点数目作为参考,与由网络得到的极值点数目进行对比的差值。

样本计算误差LossP如式(12)所示:

(12)

式中,ts是训练样本的真实值,y(x)s是网络的预测值,N是样本的数目,s是第s个样本。

极值特征误差LossE如式(13)所示:

(13)

极值特征神经网络的损失函数Loss如式(14)所示:

Loss=St·LossP+Sn·LossE

(14)

式中,St是样本误差的加权系数,取值为0.8;Sn是极值特征误差的加权系数,取值为0.2。

2 发动机缸压曲线处理

通过采集多个循环的气缸压力进行平均,得到气缸压力原始曲线。采用单输入、单输出、隐藏层9个节点的极值特征神经网络对气缸压力曲线进行降噪,并将其降噪性能与浅层神经网络和传统上处理发动机曲线的样条拟合方法进行对比。图2所示是气缸压力降噪结果。

(a) (b)

图2所示的是采用极值特征神经网络、样条方法和浅层神经网络分别对两组不同工况的气缸压力曲线进行降噪拟合,由(a)图和(b)图可以看出这三种方法的拟合曲线能还原出气缸压力原始曲线。

图3所示的是三种方法降噪结果的1阶导数对比图,图(a)和图(c)是三种方法分别对两组不同工况的气缸压力数据降噪结果的1阶导数的对比图,图(b)是图(a)在-85°～-68°曲轴转角范围内极值特征神经网络和浅层神经网络处理第一组工况的气缸压力数据降噪结果的1阶导数的放大图。

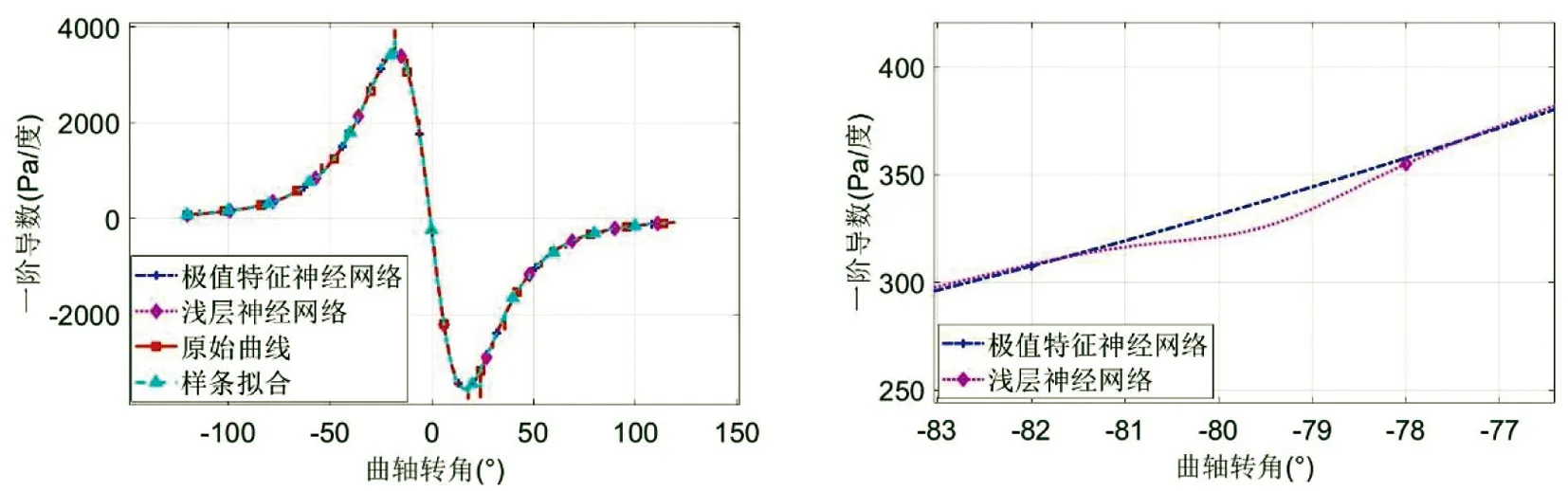
(a) (b)

从图(a)和图(c)中可以明显地看出,两组工况气缸压力数据原始曲线的1阶导数和采用样条拟合方法降噪结果的1阶导数在整个曲轴转角范围内都出现与趋势不一致的小波动,极值特征神经网络对两组工况气缸压力数据降噪结果的1阶导数和浅层神经网络对两组气缸压力数据降噪结果的1阶导数在整个曲轴范围内都比较一致。由图(b)可以看出浅层神经网络对第一组工况气缸压力数据降噪结果的1阶导数在-82°～-78°曲轴转角内出现了小波动。

图4是采用三种方法处理两组工况气缸压力数据降噪结果的2阶导数对比图。

(a) (b)

由图(a)和图(c)可以看出,极值特征神经网络和浅层神经网络对两组工况气缸压力数据降噪结果的2阶导数在整个曲轴转角范围内都比较一致,但浅层神经网络对第二组工况气缸压力数据降噪结果的2阶导数在-30°～-24°和37°～ 43°曲轴转角内出现明显的波动。由图(b)和图(d)可以看出,采用样条拟合方法对两组工况气缸压力数据降噪结果的2阶导数和两条原始曲线的2阶导数出现了大幅度的波动,出现与趋势不一致的极值点,这不符合缸内工作过程的物理特点。

图5是采用三种方法处理两组工况气缸压力数据降噪结果的3阶导数对比图。

(a) (b)

由图(a)和图(c)可以看出,极值特征神经网络对两组工况气缸压力数据降噪结果的3阶导数在整个曲轴转角范围内没有出现与整体趋势不一致的波动,没有出现异常极值点,浅层神经网络对第一组工况气缸压力数据降噪结果的3阶导数在-86°～-74°、-22°～-8°和87°～ 98°曲轴转角内出现大幅度的波动,浅层神经网络对第二组工况气缸压力数据降噪结果的3阶导数在-30°～-24°和35°～ 43°曲轴转角内出现大幅度的波动,出现了与趋势不一致的极值点。由图(b)和图(d)可以看出,采用样条拟合方法对两组工况气缸压力数据降噪结果的3阶导数和原始曲线的3阶导数出现了高频的波动,与缸内实际过程物理特征不符。

图6是采用极值特征神经网络处理6组工况气缸压力数据降噪结果图,其中图(a)是极值特征神经网络对6组工况气缸压力采样数据降噪处理后连续描绘形成的6条曲线,图(b)～图(d)是极值特征神经网络对6组工况气缸压力数据降噪结果的1～3阶导数图。

(a) (b)

由图6可以看出极值特征神经网络对6组工况气缸压力数据降噪处理的结果和对降噪处理结果的1～3阶导数能连续拟合出符合物理趋势的光顺曲线。由图(b)可以看出,6条1阶导数曲线在整个曲轴转角范围内都没有出现与趋势不一致的波动和异常极值点。由图(c)和图(d)可以看出,进气提前角15°工况的气缸压力数据降噪结果的2阶导数在-115° ～-102°曲轴转角内有小波动,进气提前角15°工况的气缸压力数据降噪结果的3阶导数在-117°～-88°曲轴转角内有小波动,进气提前角40°工况的气缸压力数据降噪结果的3阶导数在110°～ 118°曲轴转角内有小波动。

综上可以看出,采用极值特征神经网络、浅层神经网络和样条拟合方法能描绘出与原始气缸压力曲线一致的曲线。在对实测的气缸压力直接求导时,由于其存在的不规则噪声,导致其在1～3阶导数出现不同程度波动,偏离了物理真实。极值特征神经网络与其他两种降噪方法相比,极值特征神经网络具有较高的抗噪声能力,在1～3阶导数中没有出现异常极值点和波动,符合真实的物理趋势,并且通过对另外6组工况气缸压力数据降噪后求高阶导数,能排除结果偶然性的因素,进一步验证出极值特征神经网络在去噪中取得良好效果。

3 结论

通过与浅层神经网络和样条拟合方法对比,证明了极值特征神经网络对不同进气提前角工况的气缸压力数据降噪性能更好,在计算高阶导数时没有出现异常的极值点,更加符合实际的物理过程,确保了结果的可靠性和准确性。通过对另外6组工况数据进行降噪高阶分析,进一步验证了极值特征神经网络能有效抑制气缸压力曲线的噪声,对气缸压力数据降噪处理具有普遍适用性。这为气缸压力数据处理提供了新的方法。

(责任编辑 王 磊)