TM13-nXn(TM=Fe, Co, Ni; X=Si, Ge; n=1-3)团簇的结构和性质研究

刘 潇, 李沉思, 宋 薇

(河南工学院 理学部,河南 新乡 453003)

0 引言

团簇作为物质体系从原子、分子向凝聚相的过渡状态,往往表现出丰富奇异的物理和化学性质,通过探究团簇结构、性质随尺寸、组成等因素的变化,有助于人们理解和认识大块物质的起源以及材料微观结构的演变过程。在过去几十年里,团簇科学领域的科研工作者不懈努力,目的是寻找具有独特性能且高稳定性的团簇,为构建具有特殊性能的新型纳米材料奠定基础。随着研究的深入,科研工作者们发现掺杂不仅可以提高团簇的构型稳定性,还能产生不同寻常的光学、磁学和催化性质,且掺杂团簇的各种性质与团簇的大小和组成成分密切相关。因此,以掺杂团簇作为基元构造新型材料已普遍应用于发光材料、磁性材料和非线性材料等。在三维过渡金属材料中,铁系元素由于其独特的电学、催化、光学和磁学性质,成为催化、光电子、生物物理和医学领域潜在的候选材料。铁系元素包括铁(Fe)、钴(Co)和镍(Ni),其电子结构特点是最外层都有两个4s电子,但3d电子数不同,分别为6、7和8。据报道,由于掺杂铁系团簇的协同效应和可调效应,其催化活性、稳定性和选择性均优于相应的纯金属团簇,并且通过改变掺杂元素的比例,能够在一定程度上改变合金团簇的化学活性。大量研究表明,改变掺杂原子的数量和类型对掺杂团簇的电子、磁性、光学、机械、化学和其他物理性质都有所影响。

到目前为止,已有大量关于原子掺杂铁系团簇的实验和理论报道[1-11]。其中,半导体材料硅(Si)和锗(Ge)是研究者关注的重点,特别是在中小尺寸团簇的研究中[12-27],Si和Ge原子掺杂的团簇由于其独特的磁性、超导性、光电效应、热力学性质而成为研究的热点。例如,Tran等人用密度泛函理论研究了FeGen-/0(n=1—3)团簇低能态的几何和电子结构,报道了FeGen-/0(n=1—3)的基态和低能激发态的结构参数、振动频率和相对能量。他们的计算结果被用来解释FeGe3团簇的光电子能谱[12]。Deng等人利用负离子光电子能谱结合密度泛函理论计算研究了FeGen-/0(n=3—12)团簇的结构、电子和磁性[13]。近年来,我们团队也对单原子掺杂镍团簇(包括NinGe(n=19—29)团簇[25]、Nin-1X(X=C, Si, Ge, Sn, Pb; n=19—23)[26]和Nin-1X(n=19—23;X=Na—Cl)团簇[27])的磁性和电子性质,如结合能、嵌入能、电荷转移、电离势和电子亲和力进行了系统研究。然而,以上研究大多是单原子掺杂,多原子掺杂的铁系团簇至今还没有得到系统的研究。对于团簇尺度的选择上,13个原子的团簇结构一直被认为是幻数团簇,具有极高的稳定性,因此,本文对TM13-nXn(TM=Fe, Co, Ni; X=Si, Ge; n=1—3)团簇的最稳定结构进行研究,以深入了解掺杂原子的数量和类型对结构的影响,系统探讨电子性质、磁矩、结合能和电荷转移等随团簇大小的变化趋势,揭示参杂原子对团簇的结构和性能的影响规律,为合成新型磁性纳米材料提供一定的理论基础。

1 计算方法

对于团簇科学的发展,理论计算发挥了极其重要的作用。在计算分析团簇的电子结构和几何结构时,最常用的工具就是密度泛函理论(Density functional theory,DFT)。DFT在分析结构时,既能考虑电子相关作用,也能避免大体系耗时较多的不足,是一种高效的分子性质计算的方法。DFT是一种不借助任何经验参数的量子力学第一性原理理论,是研究微观体系状态、性质、材料组分、结构性能的基础。

本文采用DFT在VASP(Vienna Ab-initio Simulation Package)软件中进行计算[28-31]。VASP是一个赝势平面波软件包,电子-离子相互作用是通过投影缀加波(Projector Augmented Wave,PAW)方法描述的[32-33],并采用梯度修正函数(Perdew-Burke-Ernzerhof,PBE)的广义梯度近似(Generalized Gradient Approximation GGA)的交换关联泛函[34]。计算总能量时,考虑到计算机计算能力的局限,在比较不同的K点取值后,选取K空间的Γ点进行积分,使用真空层为20Å的简单立方单胞。由于所计算的团簇包含3d过渡金属原子,故要考虑自旋极化(ISPIN=2)。在整个计算过程中,结构和力优化的收敛标准分别是10-5eV和0.02 eV/Å。

团簇的稳定性是本文研究的重点,一般用其能量高低作为判据。结合能(Binding Energy,BE)又称为束缚能,是指团簇的总能与组成团簇的原子在自由状态下能量和之间的差值,它描述体系由自由态到束缚态的能量降低程度。为了比较方便,通常计算的是其对原子总数的平均值,即平均结合能。平均结合能可以用下式来定义:

BE(TM13)=[13E(TM)-Etotal(TM13)]/13

BE(TM13-nXn)=[(13-n)E(TM)+nE(X)-E(TM13-nXn)]/n

其中Etotal(TMn)和Etotal(TM13-nXn)表示TMn和TM13-nXn团簇的总能量。E(TM)和E(X)是自由的TM和X原子的能量。根据这个定义,BE的值越大,团簇的稳定性越强。

2 结果与讨论

2.1 TM13-nXn (TM=Fe, Co, Ni; X=Si, Ge; n=1—3) 团簇的最稳定结构

TM13(TM=Fe, Co, Ni)团簇的基态结构是一个二十面体,两个平行的五边形环以1-5-1-5-1顺序堆叠,其中一个原子位于二十面体的正中心,12个相同的过渡金属原子对称地分布在团簇的表面上,整个团簇具有Ih对称性。正是由于其特殊的结构,TM13团簇是幻数团簇,具有高度的对称性和热力学稳定性,因此对其掺杂的研究更具代表性。在选择TM13-nXn(TM=Fe, Co, Ni; X=Si, Ge; n=1—3)团簇初始结构的过程中,考虑在TM13团簇的所有可能的位置上取代1—3个TM原子获得的掺杂结构。

团簇的基态结构即全局最低能量结构,是研究团簇问题和理解团簇各种性质的关键和基础。通过DFT计算得到的TM13-nXn(TM=Fe, Co, Ni; X=Si, Ge; n=1—3)团簇的最稳定结构如图1所示。从图1中可以看出,Fe12Si团簇的最稳定结构是由一个Si原子取代Fe13团簇中心位置的Fe原子得到的,而Fe12Ge团簇的最稳定结构是由一个Ge原子取代Fe13团簇表面位置的一个Fe原子得到的。当双原子掺杂时,Fe11Ge2和Fe11Si2团簇的最稳定结构可以看成是由两个Si或Ge原子分别取代Fe13团簇顶位和下层五元环上的一个Fe原子得到的。类似的,当三原子取代时,则可以看成是在Fe11Ge2和Fe11Si2团簇的基础上继续取代下层五元环上的一个Fe原子得到了最稳定的Fe10Ge3和Fe10Si3团簇结构。

图1 在DFT-PBE水平下计算得到的Fe13-nXn(X=Si, Ge, n=1—3)团簇的最稳定结构

图2所示为Co13-nXn团簇的最稳定结构。对于Si和Ge原子掺杂Co13团簇而言,最稳定的Co12Si和Co12Ge团簇是由一个Si或Ge原子取代Co13团簇表面上的一个Co原子得到的。双原子Si和Ge掺杂Co13的最稳定结构与掺杂Fe13团簇类似,掺杂位分别是团簇表面上的顶位和下层五元环的底位。同样的,Co10Si3团簇的最稳定结构也是在Co11Si2结构的基础上再取代下层五元环间位上的一个Si原子得到的;而Co10Ge3团簇的最稳定结构则发生了变化,三个Ge原子成三角形任意取代Co13团簇表面上的三个Co原子得到的。

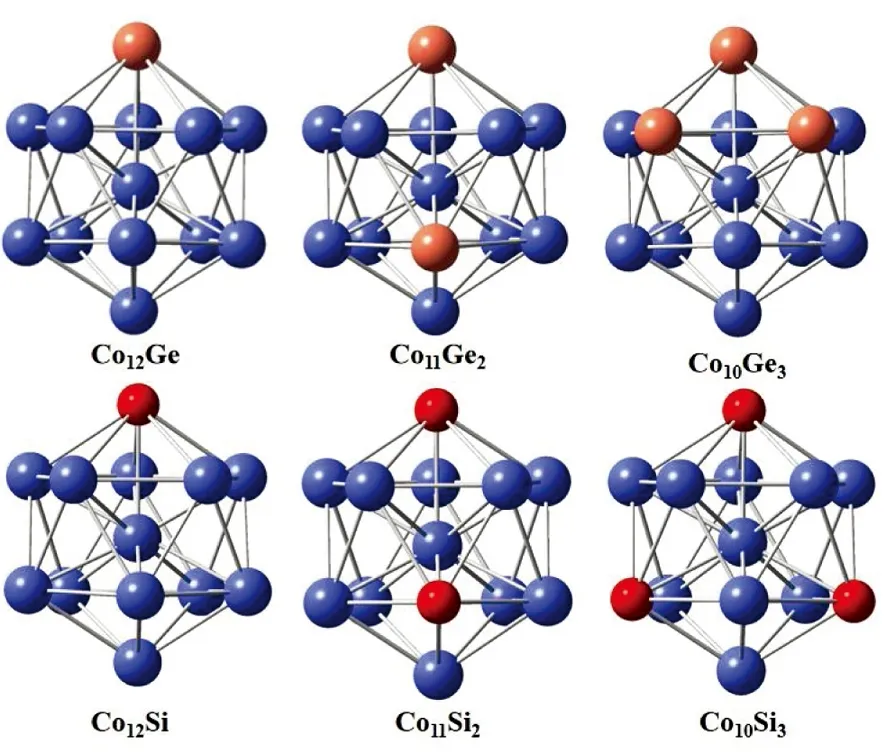
图2 在DFT-PBE水平下计算得到的Co13-nXn(X=Si, Ge; n=1—3)团簇的最稳定结构

图3所示为Si和Ge原子掺杂Ni13团簇的最稳定结构。从图中可以看出,Ni12Si和Ni12Ge的最稳定结构是由Si和Ge原子分别取代Ni13团簇表面和中心位置的一个Ni原子得到的。Ni11Si2和Ni11Ge2团簇的最稳定结构可以通过两个Si和Ge原子取代Ni13团簇表面上下两端对称的两个Ni原子获得,这两个Ni原子分别位于Ni13团簇的顶部和底部。Ni10Ge3团簇的最稳定结构与Fe10Ge3的最稳定结构相似,都是由Ge原子取代顶部以及下层五元环的间隔位的两个Ni原子构成的。而Ni10Si3团簇的最稳定结构最为特殊,三个Si原子贯穿这个二十面体结构的顶部、中心和底部构成。

图3 在DFT-PBE水平下计算得到的Ni13-nXn(X=Si, Ge, n=1-3)团簇的最稳定结构

由以上的讨论可知,单原子和三原子掺杂时,掺杂位有可能是中心位,而双原子掺杂时,掺杂位均在团簇的表面上。

2.2 相对稳定性

在团簇科学中,平均结合能是判断团簇稳定性大小的直接依据之一,平均结合能越大,热力学稳定性越好,团簇的结构就越稳定。

通过计算TM13-nXn(TM=Fe, Co, Ni; X=Si, Ge; n=0—3)团簇的平均结合能,可以分析团簇的相对稳定性,计算结果如图4所示。从图中可以看出,Si和Ge原子掺杂的团簇比相应的TMn团簇具有更高的平均结合能,这表明Si和Ge原子掺杂后增强了团簇与掺杂原子之间的相互作用,进一步提高了掺杂团簇的稳定性。随着掺杂原子数的增加,平均结合能单调增加,由此可以反映出团簇的掺杂率越高,团簇的稳定性越强。这主要是因为Si和Ge是ⅣA族元素,其最外层有四个电子,具有很高的化学稳定性,因此掺杂Si和Ge原子可以有效的提高过渡金属团簇的稳定性。对比图4(a)、(b)和(c)可以明显的观察到:TM13-nSin团簇的平均结合能增长程度高于TM13-nGen团簇,说明掺杂Si原子更有利于增强掺杂团簇的稳定性;而对比图4(d)和(e)可以看到,对于相同原子掺杂(Si或Ge),平均结合能的强弱顺序满足Fe13-nXn> Ni13-nXn> Co13-nXn团簇。即掺杂后Fe13-nXn团簇的稳定性最强,而Co13-nXn团簇的稳定性最弱。由以上的计算结果分析可知,Si原子掺杂Fe13团簇更有助于提高掺杂团簇的稳定性。

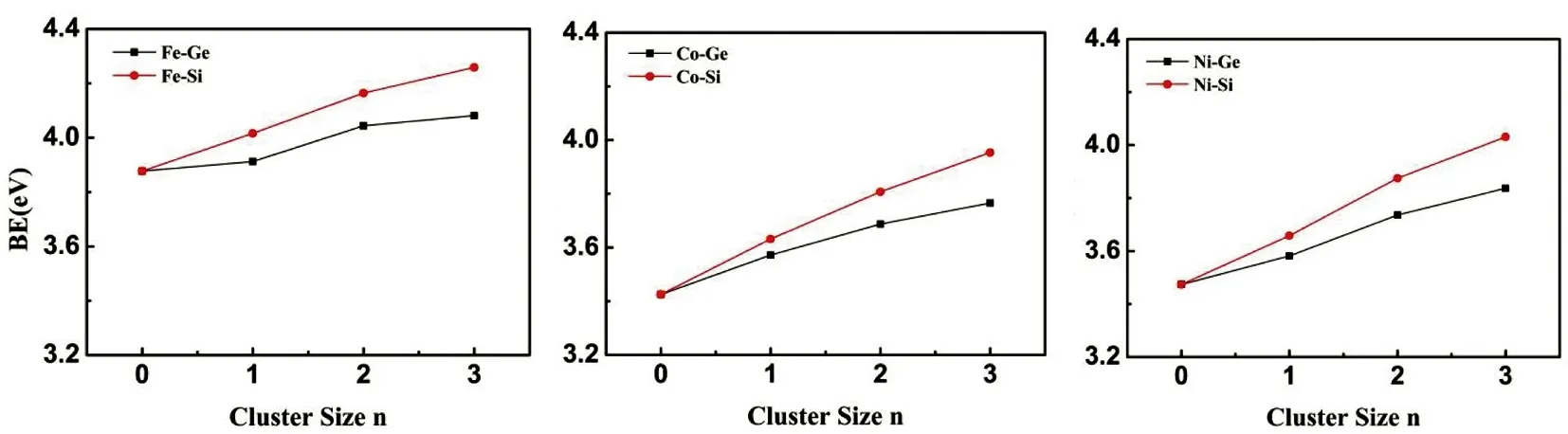
(a) (b) (c)

2.3 磁性

因在理论上和实验上应用的重要性,过渡金属团簇的磁性质一直是人们重点关注的内容。金属元素之中,Fe、Co、Ni三种金属具有铁磁性,也是应用最为广泛的磁性元素,而磁矩则是产生磁性的必要条件。团簇磁矩的大小不仅受到体系组成成分的影响,而且与体系聚集大小程度密切相关。在团簇形式下,铁系团簇的每个原子磁矩都比相应的体结构的磁矩大。Fe、Co和Ni原子的电子构型分别为3d64s2、3d74s2和3d84s2,磁矩主要是由未填充的自旋电子引起的。单个原子的磁矩是由轨道磁矩、自旋磁矩和核磁矩组成。但是核磁矩很小,通常可忽略,因此对团簇的磁化没有显著影响。但是原子磁矩并不是轨道磁矩和自旋磁矩的简单叠加,它是库仑相互作用和泡利不相容原理的共同作用的效应。最近的实验研究发现,轨道磁矩大概是自旋磁矩的10%到30%[17]。因此,本文在综合考虑计算量和精确度的情况下只考虑自旋磁矩,忽略轨道磁矩的影响。表1所示为计算得到的TM13-nXn团簇的磁矩值。从表中可以得到三条重要信息:首先,除Fe12Si团簇外,所有掺杂团簇相对于TM团簇的磁矩均减小。这是由于掺杂Si和Ge原子之后,TM原子内部轨道间存在电荷转移,使得TM团簇3d轨道的磁矩有一部分淬灭,从而导致掺杂团簇的磁矩减少。其次,除Fe11Ge2团簇外,随着掺杂原子数的增加,磁矩减小的程度更为明显,稍后我们也将通过态密度(DOS)揭开Fe12Si和Fe11Ge2两个团簇磁矩表现异常的原因;最后,掺杂Si原子的磁矩比掺杂Ge原子的磁矩减小得多。团簇掺杂后的磁矩变化范围分别为25—32μB(Fe13-nXn)、15—22μB(Co13-nXn)和2—10μB(Ni13-nXn),这表明带有可调控磁性质的团簇在磁性分子存储设备中有着潜在的应用前景。从以上分析可以总结出,改变掺杂元素的种类和比例可以有效的改变掺杂团簇的磁性。这些结论能为未来探索高选择性、高稳定性的磁性材料开辟一条新的途径。

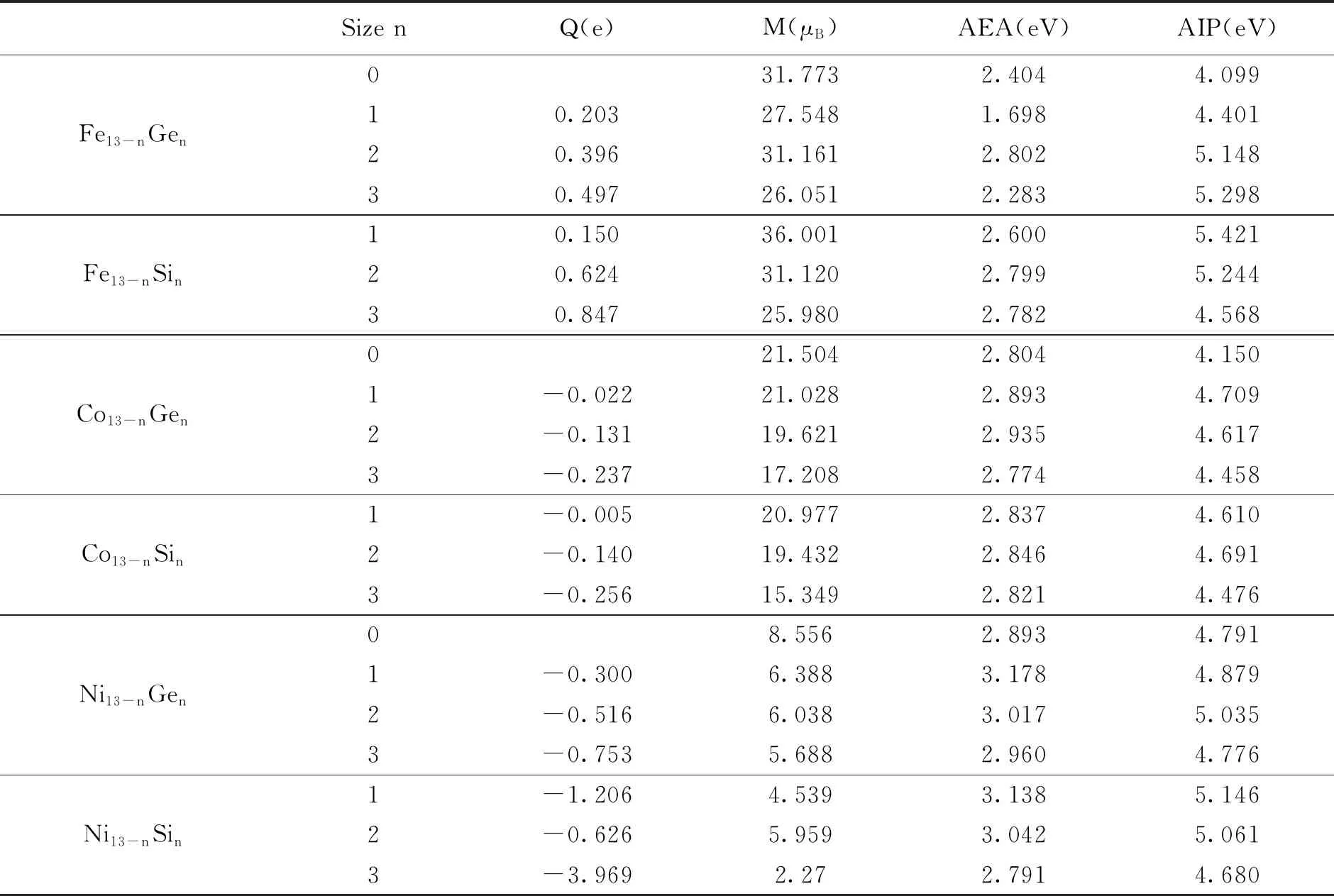
表1 DFT-PBE水平下计算得到的TM13-nXn (TM=Fe, Co, Ni; X=Si, Ge; n=1—3)团簇的电荷转移数Q(e),

2.4 电荷转移

理论计算研究中,往往通过原子的带电量来判断电子的得失数目及转移方向,然而电荷并不是一个通过测量即可得到的量,因此当选取电荷的研究方法不同时,所得到的结果也不尽相同。在掺杂团簇中,由于处在不等价空间位置的原子受到不同的势场,一部分原子将失去电荷,另一部分原子将得到电荷,从而出现电荷转移现象。Bader电荷分析表明,对于Si和Ge原子掺杂Fe13团簇而言,电荷从Fe13团簇转移到Si和Ge原子上。相反,对于Si和Ge原子掺杂Co13和Ni13团簇而言,电荷从Si和Ge原子转移到Ni13和Co13团簇上,其原因可以通过电负性来解释。电负性是元素的原子在化合物中吸引电子的能力标度,元素的电负性越大,表示其原子在化合物中吸引电子的能力越强。Fe、Co、Ni、Si和Ge元素的电负性分别是1.83、1.88、1.91、1.90和2.01。其中Fe原子的电负性最小,因此电荷从Fe13团簇转移到Si和Ge原子上。而Co和Ni原子的电负性与Si原子接近,比Ge原子的略小,但由于团簇的原子个数较多,结合力较强,故电荷也从Si和Ge原子转移到Co13和Ni13团簇上。此外从电荷转移量上看,对比Si和Ge原子的电荷转移情况可知Si原子的电荷转移量更多;对比转移到Co13和Ni13团簇的情况可知,转移到Ni13团簇上的电荷量更多。同时也可以观察到掺杂原子数与电子转移数成正比,即掺杂原子数越多,电荷转移量也越多。

2.5 态密度(DOS)

团簇结构确定后,可以通过电荷密度图分析团簇之间的成键性质以及电子云的轨道性质。在固体物理及凝聚态物理中,态密度描述了在单位能量间隔内系统电子可以占据的状态数,系统的态密度分布一般是连续取值。态密度高的地方说明可占据的状态数多,态密度为零则说明该能级处没有允许电子存在的态。因此态密度图能反映出电子在各个轨道的分布情况,也能够反映出原子与原子之间的相互作用情况,并且还可以揭示化学键的信息。

从之前磁矩的分析可知,掺杂后Fe11Ge2和Fe12Si团簇的磁矩不降反增,因此要通过计算Fe13、Fe11Ge2以及Fe12Si团簇的分波态密度图(PDOS)分析其原因。如图5所示,中间垂直的虚线代表费米能级的位置,自旋向上和向下的态分别呈现在图的上半部分和下半部分。从图中可以看出,在费米能级以下,图中所有团簇自旋向上态的积分面积明显大于自旋向下电子态的积分面积,对称性不均匀,表明团簇中存在大量未成对电子,而未成对电子的自旋又产生磁矩,因此Fe13、Fe11Ge2以及Fe12Si团簇表现出强磁性,磁矩值分别是31.773μB、31.161μB和36.001μB。

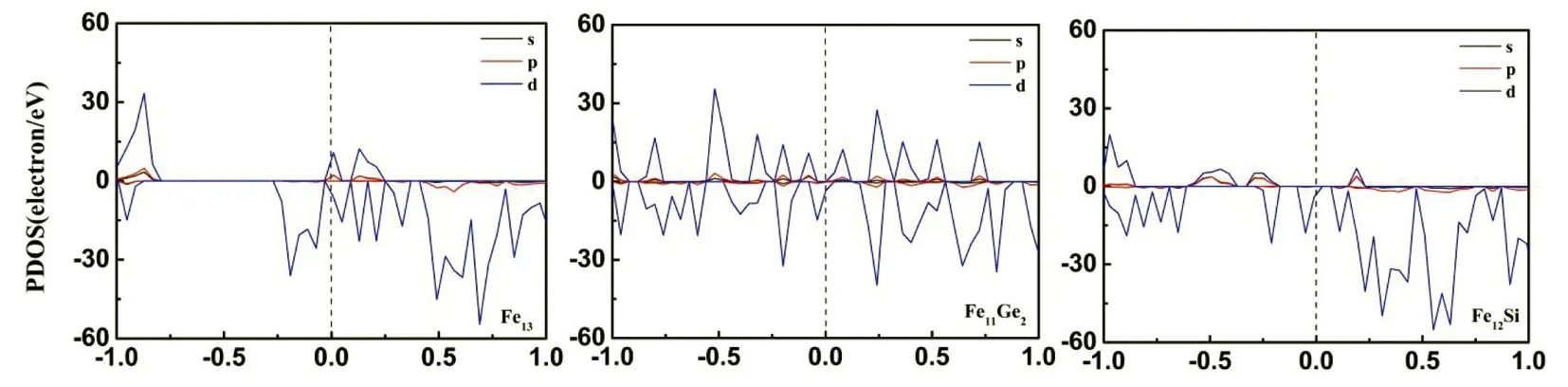
(a) (b) (c)

图6所示为局域态密度图(LDOS),从图中可以更好地了解轨道杂化对磁性的影响。对比Fe13团簇的PDOS结果(图5(a))可知,Fe11Ge2和Fe12Si团簇的LDOS中Fe的d轨道与Ge的p轨道(图6(a))或Si的p轨道(图6(b))之间发生了强杂化作用,因此出现了明显的杂化峰。由于Fe-Ge和Fe-Si之间的杂化作用,Ge和Si原子的自旋极化增强了。此外从图中也可以观察到,电子的态密度主要由d电子壳层决定,s和p电子对净自旋的贡献很小。因此,掺杂原子的类型和数量对团簇的磁性有一定的影响。

(a)

2.6 电离势和电子亲和势

绝热电子亲和势(AEA)表示团簇从阳离子状态到相应中性基态所引起的能量变化。绝热电子亲和势反映了元素原子得电子的能力,亲和能越大,团簇越容易得到电子,团簇的非金属性也愈强。相反绝热电离能(AIP)是基态的气态原子失去电子变为气态阳离子,必须克服核电荷对电子的引力而所需要的能量,因此电离能越低,团簇越容易失去电子。AIP和AEA是中性团簇和离子团簇的总能量差,其定义如下:

式中,ET为DFT-PBE计算的TM13-nXn(TM=Fe, Co, Ni; X=Si, Ge; n=1—3)团簇的总能量。

从表1中可以看出,当TMn团簇掺杂了Si和Ge原子之后,大部分团簇的电子亲和势值增加了,说明掺杂团簇的非金属性增强,得电子能力有所提高。同时电离能值也增加,进一步说明了掺杂团簇的失电子能力减弱了。由此可见,掺杂Si和Ge有助提高掺杂团簇的非金属性质,增强团簇的稳定性。

3 结论

本文采用DFT方法,系统研究了TM13-nXn(TM=Fe, Co, Ni; X=Si, Ge; n=1—3)团簇的几何结构,电子结构、相对稳定性、电子性质以及磁性。结果表明,掺杂Si和Ge原子后的TM13-nXn团簇的稳定性均有所增强,除Fe12Si团簇外,掺杂团簇的磁性都有不同程度减弱;由于电负性的不同,对于Fe团簇而言,电荷转移从Fe团簇到掺杂原子上,相反对于Co和Ni团簇而言,电荷从掺杂原子转移到Co和Ni团簇上;根据绝热电子亲和势和绝热电离势的结果可知,掺杂团簇的非金属性提高,吸电子能力增强。本工作不仅有利于人们从理论上深入认识掺杂原子的数量和种类对团簇的结构以及性质的影响,而且对于合成一些新型磁性纳米材料具有一定的参考意义。

(责任编辑 吕春红)