基于实时交通信息的PHEV模型预测控制策略研究*
张冰战 朱昊 康谷峰 李开放 朱茂飞
(1.合肥工业大学,合肥 230009;2.汽车技术与装备国家地方联合工程研究中心,合肥 230009;3.合肥学院,合肥 230601)
主题词:插电式混合动力汽车 实时交通信息 车速预测 能量管理策略 模型预测控制
1 前言
插电式混合动力汽车(Plug-in Hybrid Electric Vehicle,PHEV)能量管理策略通过实现发动机和电机功率或转矩的合理分配,提高整车的燃油经济性,同时满足其动力需求[1]。在当前对控制策略的研究中,基于规则的能量管理策略最常使用,但其过于依赖工程师的开发经验,且对工况的实时适应性不足,无法达到经济性最优[2]。基于优化的管理策略分为全局最优和局部最优2 种:局部最优策略可以实现瞬时的最佳经济性,但无法保证完整行程内经济性最优[3];全局优化策略需要提前确定整个行驶工况,要求比较严苛[4]。
近年来,学者们将研究重点从实现全局最优向预测时域内滚动优化的预测控制策略转变,实现该策略的控制效果需要对未来车速进行准确预测。杨亚联等[5]根据工况数据建立了高阶马尔可夫车速预测模型,相比一阶马尔可夫预测模型,预测精度有所提高,但仍存在模型建立较复杂、实用性差等不足。谢浩等[6]采用遗传算法和粒子群算法对反向传播(Back Propagation,BP)神经网络预测模型进行优化,单个模型预测精度得到提高,但基于预测结果仍难以获得理想的车速拟合结果。Baker 等[7]对未来车速进行预测时,以历史车速信息和经度作为输入,预测精度有所提高。连静等[8]充分考虑了驾驶员对未来车速变化趋势的影响,预测精度有所提高,并将预测模型嵌入模型预测控制策略。
本文针对动态规划需先确定行程工况的缺点,提出一种结合实时交通数据进行车速预测的方法,以采集到的车速信息和交通流密度信息作为输入,选择均方根误差最小作为目标,得到未来一段时间内的车速,应用动态规划(Dynamic Programing,DP)方法求出阶段性的最优解并向后循环推进,进而使用基于模型预测控制(Model Predictive Control,MPC)的方法完成能量管理策略的搭建。
2 整车模型
2.1 车辆架构及参数
通过对PHEV各种架构的分析,选用插电式并联混合动力汽车,驱动系统架构如图1所示。该驱动系统由发动机、电机、动力电池、转矩耦合器、变速器、主减速器等部件组成。
2.2 关键动力部件模型
在ADVISOR/Simulink软件环境下,将试验数据融入理论建模方法,分别建立发动机、电机、电池和整车纵向动力学模型。这种建模方法在提高模型准确性的同时可以简化建模过程,为后续能量管理策略研究奠定基础[9]。
2.2.1 发动机模型
本文利用试验获得的发动机燃油消耗率等数据建立发动机模型。发动机燃油消耗率be取决于发动机的即时扭矩和转速:
式中,Te为发动机输出扭矩;ne为发动机转速。
根据三者间关系得到的发动机燃油消耗率MAP图如图2所示。
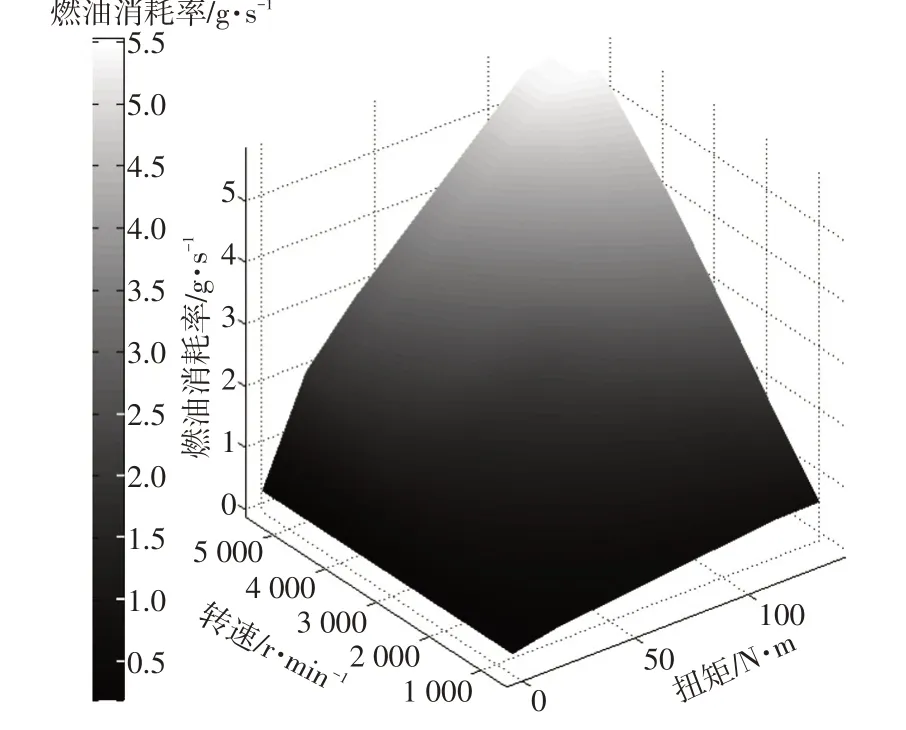
图2 发动机燃油消耗率MAP图
发动机效率为:
式中,b(Te,ne)为发动机瞬时燃油消耗率;Hu为燃油热值。
发动机效率曲线如图3所示。
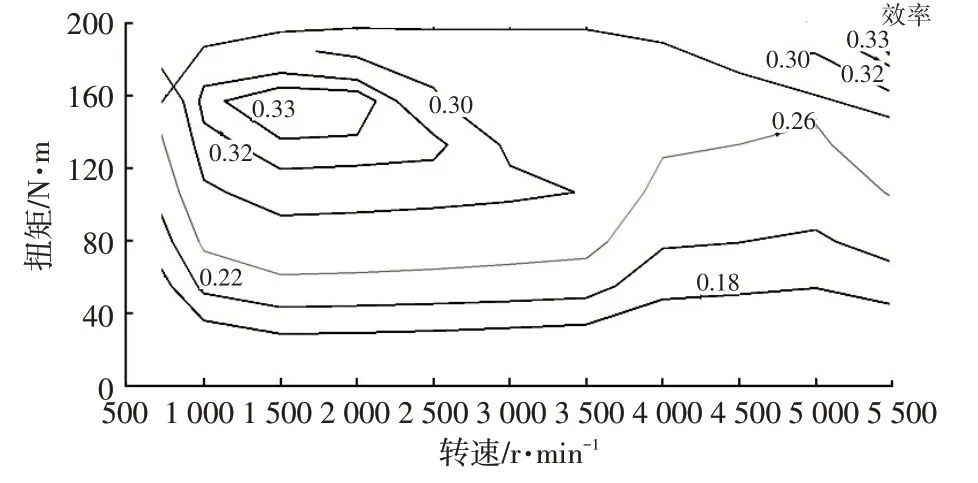
图3 发动机效率曲线
2.2.2 电机模型
在插电式并联混合动力汽车中,电机不仅提供驱动力,而且在汽车下长坡、紧急制动等减速工况下可进行能量回收。电机的充放电效率可根据电机输入和输出功率间的关系获得:
式中,nm为电机转速;Tm为电机转矩;Im为电机内部电流;Um为电机内部电压。
Tm>0 时,电机作为电动机使用,由式(3)可得电机的驱动效率,Tm<0 时,电机作为发电机使用,由式(3)可得电机的制动效率,且驱动效率和制动效率关于转矩为0的直线对称。电机效率曲线如图4所示。

图4 电机效率曲线
2.2.3 动力电池模型
本文对电池组的关注重点在于其输入输出特性,因此在仿真软件中建立简单的内阻模型即可。其等效电路如图5所示。

图5 电池等效电路示意
电池荷电状态(State of Charge,SOC)变化的传递公式为:
式中,ISOC,0为电池组荷电状态初始值;C为电池容量;ηba为电池充放电效率;Iba为电池内部电流。
2.2.4 整车纵向动力学模型
本文针对PHEV 能量管理策略的研究仅关注汽车的动力性与燃油经济性,不需要考虑汽车的复杂受力状况,只考虑汽车的纵向受力情况,如图6所示。

图6 整车纵向受力示意
汽车的行驶动力学方程为:
式中,Ft=Tw/r为驱动力;Fw=CDAv2/21.15 为空气阻力;Ff=mgfcosα为滚动阻力;Fj=δm·dv/dt为加速阻力;Fi=mgsinα为坡度阻力;Tw为车轮转矩;r为车轮滚动半径;CD为空气阻力系数;A为汽车迎风面积;v为车速;m为汽车满载质量;g为重力加速度;f为滚动阻力系数;α为道路坡度角;δ为旋转质量换算系数。
可得汽车行驶过程中的车轮转矩为:
车轮转速为:
3 基于实时交通信息的车速预测方法
高精度的车速预测可实现短期预测时域内的全局最优控制,对制定高效的PHEV 能量管理策略至关重要[10]。由于只考虑历史车速信息作为输入时预测精度较低,本文在复杂道路工况基础上,通过交通流建模的方式获取车速、交通流量等实时交通信息,将历史车速和实时交通信息结合进行未来车速的预测[11]。
3.1 基于VISSIM的交通流建模
交通路网作为交通运行的必要场景,其复杂度直接影响到车辆与周围交通环境的相对关系。本文采用VISSIM 实现交通流模型构建,模拟车辆在所建立的交通环境下的行驶状态,获取实时交通信息,为后续车速预测提供数据来源[12]。以合肥工业大学屯溪路校区到翡翠湖校区之间的实时环境作为对象,建立城市道路交通网络。
考虑到该环境下多为高架道路行驶,模型中设定行人不参与交通行为,简化建模和数据采集的流程。道路总长约为14 km,其中包括了城市道路、高架道路、十字路口等道路元素,根据实际考察设定了车流量、期望速度、期望加速度、信号灯切换原则等,具体建模流程图7所示。
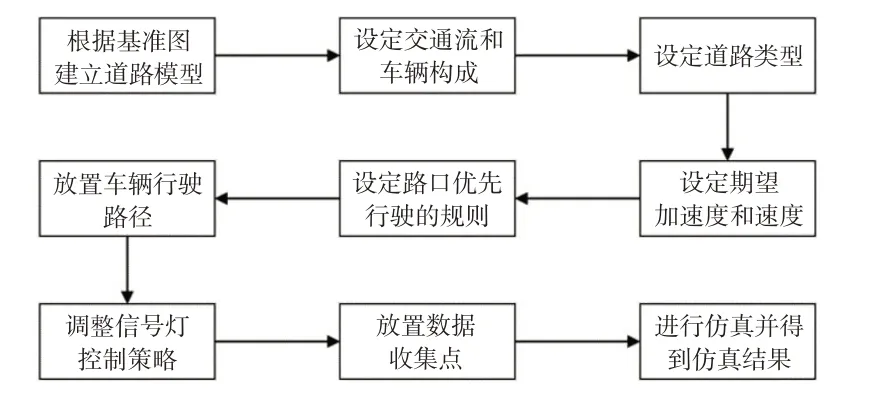
图7 交通流模型建立流程
考虑到行驶过程中支路车辆会向主干道行驶,根据考察结果确定主干道不同地点处的支路情况以及支路车流量信息,以此为根据设定道路车流量信息,确保模型贴合真实交通情况,最终建立的路网模型如图8 所示,箭头所包括范围为同一类型道路。其中,城市道路存在交叉路口和道路交汇处,直线段后半部分为高架道路,弧线部分由前半部的高架道路和后半部的城市道路组成,高架道路存在多个出口,城市道路较为复杂,存在多个交叉路口,影响交通流量。
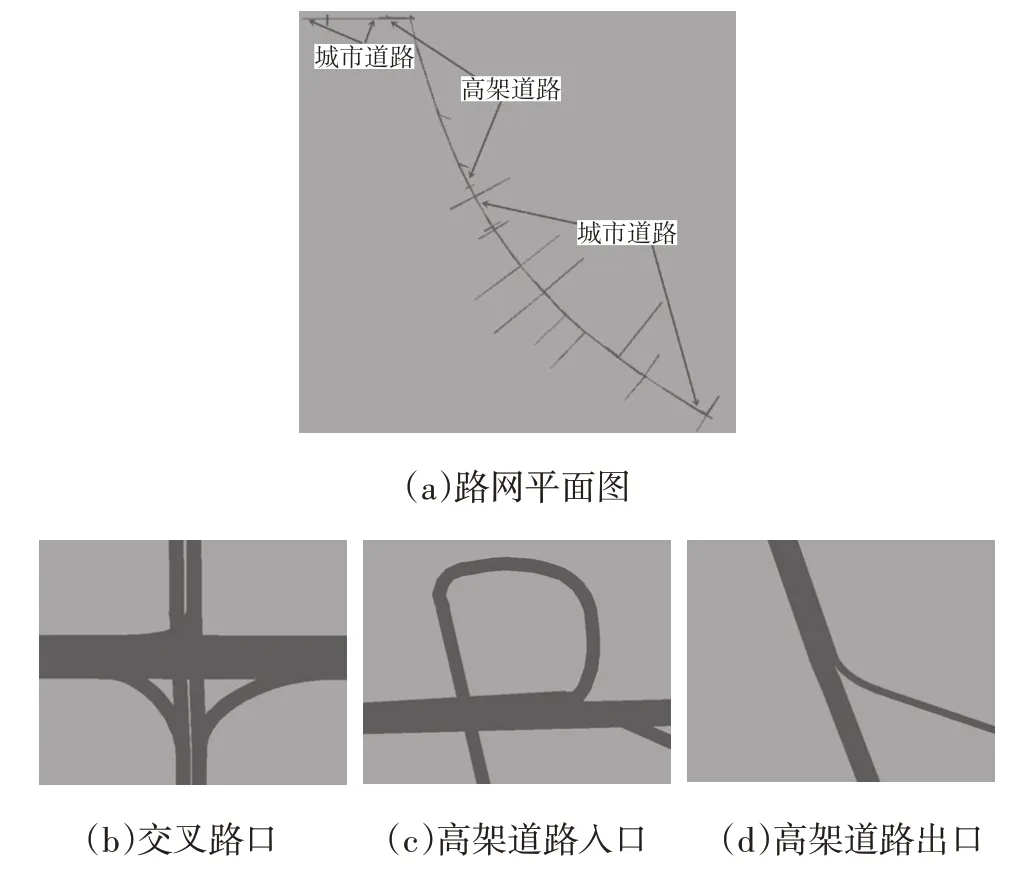
图8 路网平面图及部分三维图
在模型中设立监测点来采集不同时刻的车流密度、车辆平均速度和车辆平均加速度等信息。由于将车流密度定义为100 m范围内的车辆数量,且要考虑到车道数以及不同道路情况的影响,将车流密度进行规则化,以-1表示道路畅通,0表示道路车流量正常,1表示道路拥堵。由于设置路况较为复杂,收集到的数据需要进行相应处理,得到最终交通信息数据集。根据采集到的数据以及数据处理结果,得到仿真结果如图9、图10所示。

图10 交通流模型车流密度分布
3.2 径向基函数神经网络建模
在径向基函数(Radial Basis Function,RBF)神经网络中,在网络结构的输入层存放输入信号数据的节点。隐含层的节点数量根据具体需解决的问题动态改变,输出层一般为简单的线性函数,对输入模式作出响应,RBF隐含层神经元模型如图11所示。
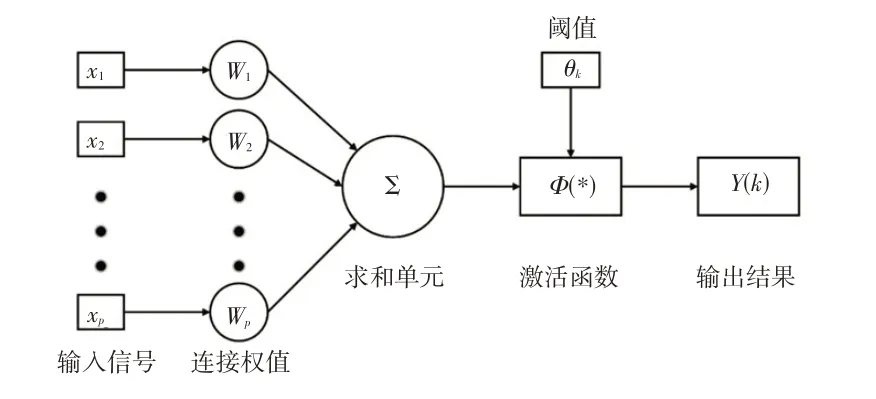
图11 RBF隐含层神经元模型
首先确定输入和输出,选用当前时刻的交通流量和车速信息、历史车速信息作为输入,以预测的车速作为输出,预测复杂道路情况下的车速情况,再将交通流模型数据中70%的数据作为样本进行模型训练。最后建立RBF 神经网络模型,通过对实时交通信息样本的学习训练,建立基于实时交通信息和预测车速之间的非线性映射关系,即车速预测模型:
式中,Fnet为生成的径向基神经网络模型;Fnewrbe为构建径向基神经网络函数;xtrain为输入的实时交通信息向量;ytrain为输出的未来预测车速向量;sspr为径向基函数的扩展速度,缺省值为1。
RBF神经网络车速预测模型如图12所示。
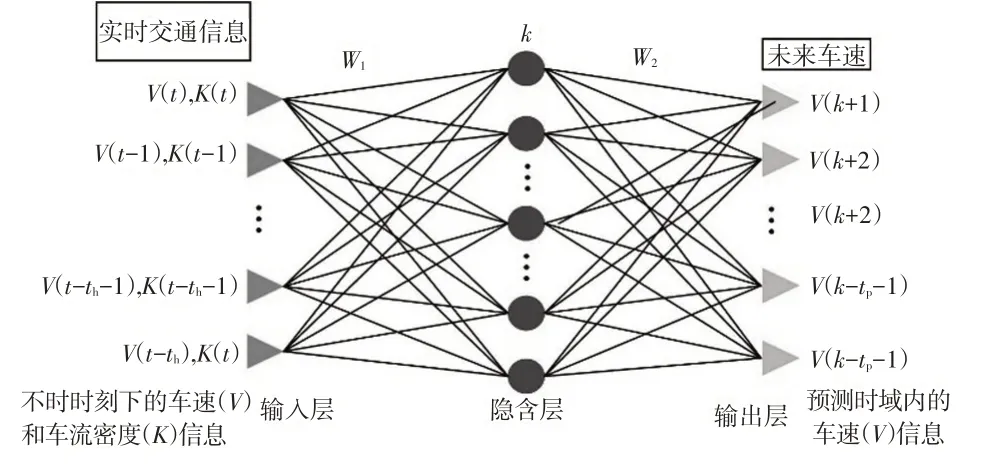
图12 RBF神经网络车速预测模型示意
3.3 车速预测和结果分析
在RBF 神经网络车速预测模型建立过程中,发现影响预测结果的是所选择的交通信息时间长度和sspr,故针对这2 个影响因素对多步预测进行研究。选定一定时间长度范围的历史车速和实时交通流密度,求出不同时间长度下所对应的sspr,通过训练得到适应性强的预测模型。其误差和方差计算公式为:
式中,e、eRMSE分别为任意时刻预测时域和整体预测过程的均方根误差;th、tp分别为预测模型的输入历史时长和预测时域时长;vi,p为i时刻下的预测车速;vi,r为i时刻下的实际车速;N为预测工况的循环长度;ej为j时刻下的预测误差。
综合分析车速的多步预测过程,考虑到预测时域越长,预测精度越低,经过仿真分析,选取历史时长为10 s,预测时域为3 s进行仿真。为了验证该预测方法的准确性,本文对仅基于历史车速的传统车速预测方法和基于实时交通信息的车速预测方法进行对比验证。由于输入的不同,sspr有所变化,根据不同的输入,得到其最优值进行预测,其结果如图13所示。
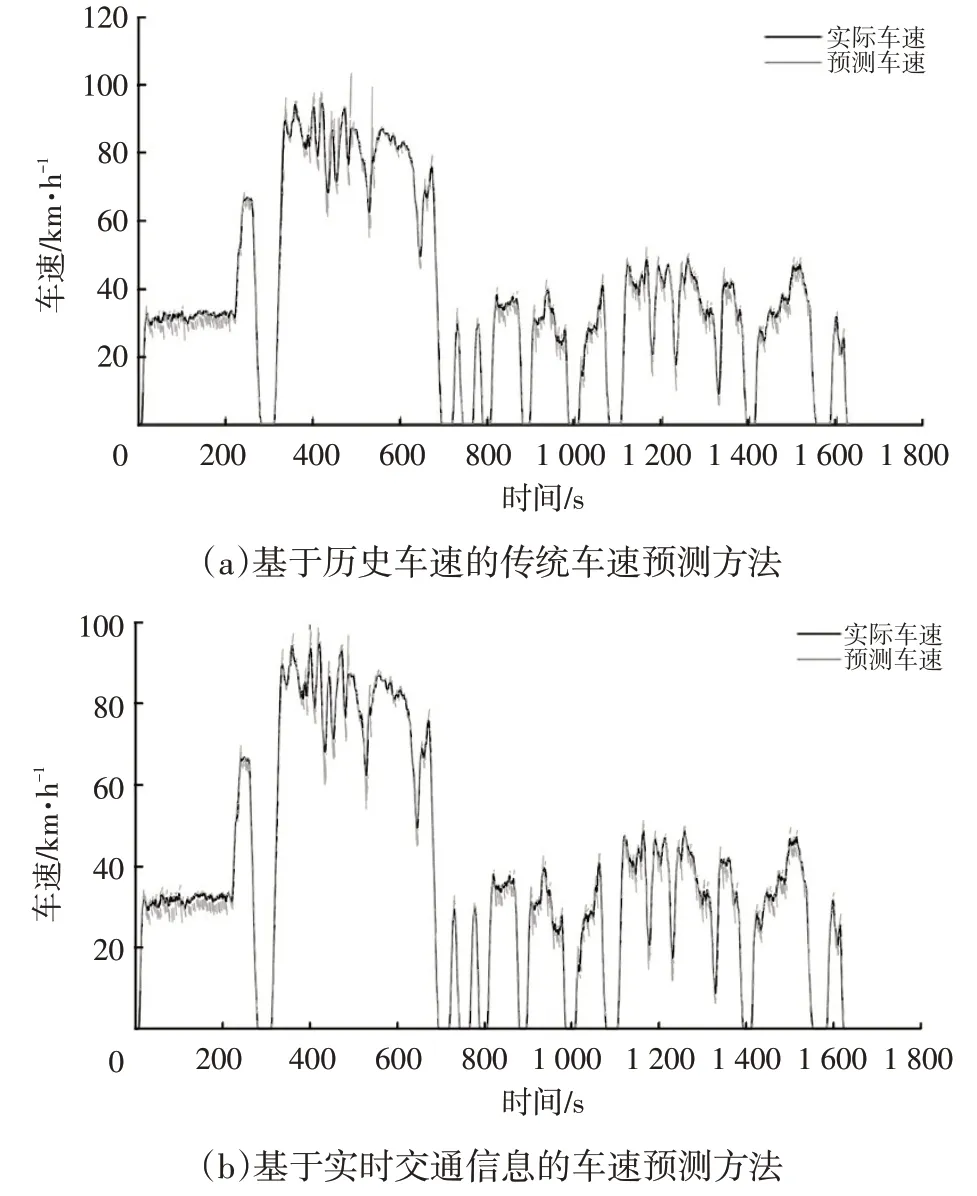
图13 车速预测结果对比
由图13可以看出,在未考虑车辆密度的情况下,仅依赖历史的实际车速进行预测,在车流密度突然变化的情况下,预测误差较大。在第350~650 s 区间内路段车流密度变化,导致车辆加减速时,结合车流密度的输入,基于实时交通信息的车速预测方法预测更为准确。为对预测结果进行更加合理的评价,采用均方根误差作为指标进行评价,结果如表1所示,由表1可以看出,相较于仅考虑历史车速的车速预测方法,结合车流密度的实时交通信息的预测方法预测精度大幅提升,达到了13.5%。
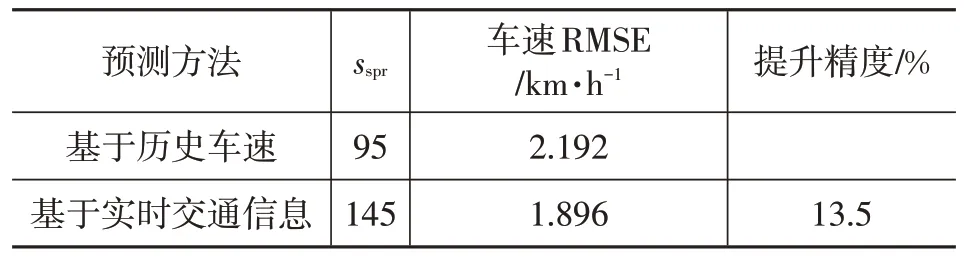
表1 车速预测指标
4 基于车速预测的能量管理策略
将径向基神经网络车速预测模型嵌入模型预测控制中,制定基于实时交通信息的模型预测控制(Model Predictive Control based on Traffic,MPCT)能量管理策略,根据得到的车速预测模型预测未来短期内的车速信息,利用整车纵向动力学模型求解整车需求转矩,采用动态规划算法在一定的约束条件下求解该时域内最优电机转矩序列和最优挡位传动比序列;把计算得到的最优控制序列的第1个值施加给车辆,更新汽车的行驶状态,计算出下一时刻的SOC;进入下一时刻,再次获取当前实时交通信息,预测未来短期的车速信息,校正上一时刻的预测值,进行车速预测、滚动优化和反馈校正,直至行程终止。其求解流程如图14所示。

图14 基于实时交通信息的MPC能量管理策略求解流程
4.1 基于实时交通信息的MPC能量管理策略
混合动力汽车的能量管理问题是在多种约束条件下对汽车行驶过程中的功率进行合理分配,达到燃油消耗量最小的典型多阶段决策问题[13]。本文采用动态规划方法对汽车的能量管理问题进行优化求解,实现全局最优。选择动力电池SOC 作为该动态规划方法的状态变量,第k阶段的状态变量表达式为:
式中,ISOC,k为k阶段动力电池的荷电状态。
PHEV 能量管理策略的目标是合理分配发动机和电机的转矩,转矩的不同分配情况导致消耗的电量不同[14]。本文选取电机转矩Tm和变速器挡位Y作为控制变量:
式中,uk为第k阶段的控制变量;Tm,k为第k阶段电机输出转矩;Yk为第k阶段变速器挡位。
本文选取每一阶段的燃油消耗量作为代价函数,行程中总的燃油消耗量为动态规划的目标函数:
式中,Qk为第k阶段发动机的燃油消耗量。
在整个过程的任一阶段,将控制变量作用于整车能量管理系统,电池SOC将会转变为下一个阶段的对应状态,将控制变量和状态变量代入即可求得动态规划方法的状态转移方程:
式中,Δt为系统在离散过程中选择的时间的离散度。
相比较于传统MPC 策略,考虑交通信息的MPC 策略的目标在于利用交通信息改善车速预测精确度,根据可靠的未来车速信息计算整车的需求转矩,在发动机和电机之间进行合理功率分配,既能够满足行驶需求,也能让发动机始终工作在最优工作区域内。首先将历史车速和交通流密度作为车速预测模型的输入,得到预测时域内的车速信息,计算预测时域内的整车需求转矩,然后根据当前SOC和整车需求转矩,采用动态规划方法求解最优的电机转矩和传动比序列,以此为基础更新车辆的行驶信息并计算下一时刻的SOC,最后进入下一时刻,重复该过程,直到结束。
4.2 动态规划方法
预测时域内汽车的优化控制是一个非线性有约束的全局优化问题,选择SOC 为状态变量,电机输出转矩和变速器传动比为控制变量,发动机燃油消耗量作为目标函数,在预测时域[k,k+tp]内建立优化求解模型:
整车驱动系统各部件都有可行的工作范围,出于对这些部件的保护以及部件本身参数的限制,需要为其增加一些限制条件:
式中,Tmmin、Tmmax分别为电机的最小、最大转矩;nmmin、nmmax分别为电机的最小、最大转速;Temin、Temax分别为发动机的最小、最大转矩;nemin、nemax分别为发动机的最小、最大转速;ISOC,min、ISOC,max分别为动力电池SOC的最小、最大值;nm,k为第k阶段电机转速;Te,k、ne,k分别为第k阶段发动机转矩、转速;。
预测时域内的状态转移方程为式(15)。对于模型预测控制系统的第k阶段,在预测时域[k,k+tp]内,以采用动态规划算法求解电机最优转矩序列为例说明模型预测控制的具体求解过程[15],如图15所示。在预测时域内的每一时刻遍历求出所有状态变量和控制变量的可行解并记录保存,再根据初始条件求出该时域内的最优控制序列并施加于汽车。
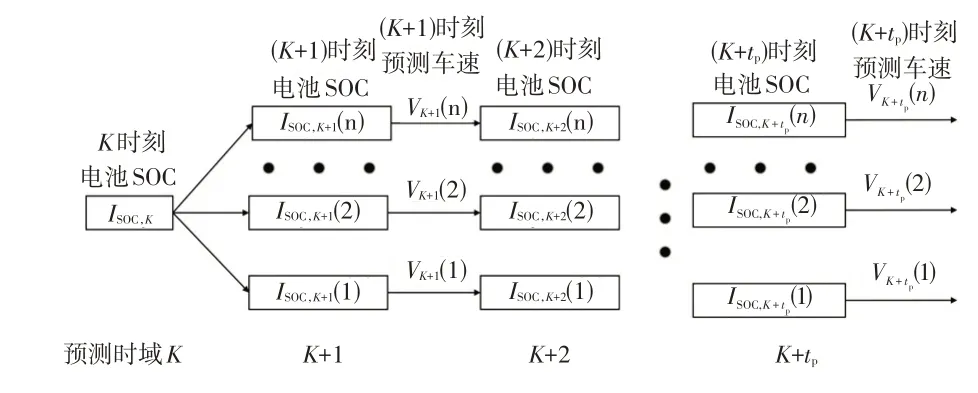
图15 预测时域内的求解过程
4.3 仿真结果分析
为验证本文所提出的能量管理策略的有效性,利用MALTAB/Advisor 平台进行仿真分析。车辆主要参数如表2所示。

表2 车辆主要参数
设定初始SOC为0.7,终止SOC为0.45,输入的历史交通信息时长为10 s,预测时域为3 s,仿真工况为所采集到的实际道路工况,将所设计的MPCT能量管理策略与基于电量保持-电量消耗(Charge Depletion-Charge Sustaining,CS-CD)的规则策略、基于动态规划的优化能量管理策略和基于MPC的能量管理策略进行对比,4种策略的仿真结果如图16~图18所示。
由图16 可以看出,实际的车速与目标车速基本保持一致,跟随的车速误差值在2 km/h 范围内,表明所提出的能量管理策略能够很好地实现整车控制功能。
由图17可以看出:实际工况前期车辆速度较低,且伴随着相应的减速制动情况,基于DP和基于MPC的能量管理策略可有效实现制动能量回收,基于CD-CS 的策略在制动能量回收方面效果不理想;随着工况中期处于高速路段,SOC下降速度变快,基于CD-CS策略对电量利用率不高,SOC 下降缓慢,其余3 种策略的发动机输出转矩很大,电机转矩为负,处于发电机模式,为动力电池充电,电池的SOC 出现轻微上升,MPCT 策略的能量回收效率更高;工况后期道路情况复杂,CD-CS 策略完全依赖于发动机工作,相比于MPC 策略,MPCT 的策略更多依赖于电动机实现驱动;在整个实时工况中,DP算法的SOC 终值最低,相比于MPC 策略,MPCT 的策略在电量利用上有所提升,满足动力要求的同时减少了燃油消耗量,可看出MPCT策略的优异性。
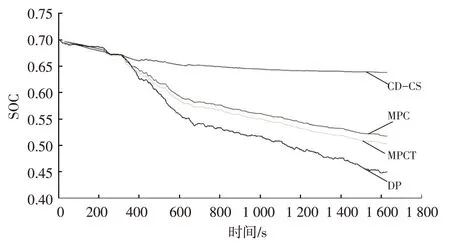
图17 不同策略下的SOC变化曲线
由图18可以看出,CD-CS策略的燃油消耗量最高,且随着道路交通复杂程度变化,其燃油消耗量增加也越多,通过曲线态势可以看出,MPCT 策略比MPC 策略更优异,与DP 策略相接近,前期处于高速道路时,燃油消耗量基本持平,当进入市区道路后,MPCT 策略的燃油消耗量曲线位于MPC策略曲线下方,可见MPCT策略在复杂道路工况下的能量分配更为优异,对燃油的消耗更少,验证了其有效性。
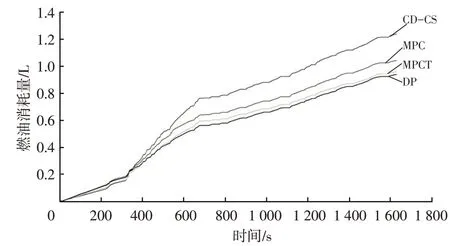
图18 不同策略下的燃油消耗曲线
考虑混合动力汽车的特性,采用等效燃油消耗方法将电量消耗转换为燃油消耗量,以此作为对比不同策略下的PHEV 的百公里燃油消耗量的评价指标。本文选用燃油等效因子进行等效燃油消耗量计算[16],考虑工况、发动机和发电机效率等因素,选取燃油等效因子为3,即1 L燃油消耗量约对应3 kW·h耗电量,根据SOC和电池总容量进行耗电量与燃油消耗量的转换,计算百公里燃油消耗量,如表3所示。由表3可以看出,对于道路实际工况,CD-CS 策略的百公里等效燃油消耗量最高,DP策略的百公里等效燃油消耗量最低。

表3 不同策略下的燃油消耗量对比
5 结束语
本文针对插电式混合动力汽车建立了一种基于实时交通信息的MPC 能量管理策略,首先基于VISSIM 软件搭建了道路交通模型,采集实时道路交通信息,建立基于RBF 神经网络的车速预测模型,根据均方根误差最小原则选取网络参数,通过实时交通信息与车速数据的融合,得到更加精确的车速预测结果,与基于历史车速信息的车速预测结果进行对比分析,验证了该预测模型的有效性,同时验证本文能量管理策略的有效性,在实时道路工况下,整车燃油经济性相比较于MPC 策略提高了9.5%。

