基于随机动态规划的PHEV队列分层优化控制策略研究

朱兰馨 周长登 崔佳伦

（1.昆明理工大学，昆明 650500；2.中国船舶重工集团公司第705研究所昆明分部，昆明 650101）

主题词：分层优化 径向基神经网络 随机动态规划 马尔可夫链

1 前言

智能网联汽车队列控制在确保安全行驶的前提下，可以有效保持队列车辆间的距离，减少不必要的速度变化，从而增强道路通行能力、提高交通安全性、缓解环境污染[1]。近年来，大量学者针对汽车队列控制问题展开了研究。李鹏飞等[2]搭建了模糊神经网络跟车控制器，使车速和车距控制更平滑。随着研究的深入，在实现车速规划的同时提升经济性成为研究重点，Ma等[3]、孙涛等[4]基于模型预测控制（Model Predictive Control，MPC）实现了队列车辆安全距离、加速度、燃油经济性的多目标优化。然而，上述研究对象均为单一能源车辆，针对混合动力车辆队列，如何在确保速度规划的同时设计合理的能量管理系统（Energy Management System，EMS），是学术界的研究难题，分层控制框架独特的分层架构可以实现ACC与EMS之间信息的单向传递[5]，有效解决了这一问题。HomChaudhuri 等[6]采用等效燃油消耗最小策略（Equivalent Consumption Minimization Strategy，ECMS）搭建下层EMS 控制器，基于上层提供的车速、需求功率实时调整发动机及电机功率。为提升分层策略控制效果，需开发合适的EMS 下层控制器。

目前，EMS 可分为2 种类型：基于规则的方法[7]和基于优化的方法[8]。基于规则的方法过于依赖工程经验[9]，然而汽车实际行驶工况多变，仅依赖专家工程经验来设定混合动力车辆的能量分配规则，很难确保车辆达到最优的经济性。基于优化的策略可以分为2个类别，即瞬时优化[10]和全局优化[11]。瞬时优化的典型算法为ECMS、MPC[12]，仅能保证车辆能耗局部最优[13]。全局优化可实现全局最优，典型的算法为动态规划（Dynamic Programming，DP），DP 需提前获取工况信息，才能利用全局最优化理论分配不同能源间的输出功率[14]。随机动态规划（Stochastic Dynamic Programming，SDP）在DP的基础上结合了马尔可夫决策过程，确保算法具备求解随机过程问题的能力[15]，因而SDP 更适用于PHEV 的EMS开发。

针对上述研究现状，本文采用基于SDP的多能源功率分配方法搭建下层EMS 控制器，利用马尔可夫决策过程提高其最优性和实时性，上层设计基于RBFNN 与MPC 结合的速度优化控制器，确保速度和距离跟踪的及时性和平稳性。下层EMS控制器根据上层控制器传递的车速、需求功率、荷电状态等信息，利用SDP算法实现PHEV 的发动机与动力电池之间的最优能量分配。最后，仿真验证所提出算法的有效性。

2 插电式混合动力汽车动力系统建模

2.1 车辆模型

本文的研究对象为基于双电机与发动机3 个动力源的混合动力汽车。车辆动力系统结构如图1所示，驱动模式包括纯电动驱动、发动机驱动、串并联驱动及能量回收模式。整车具体参数如表1所示。

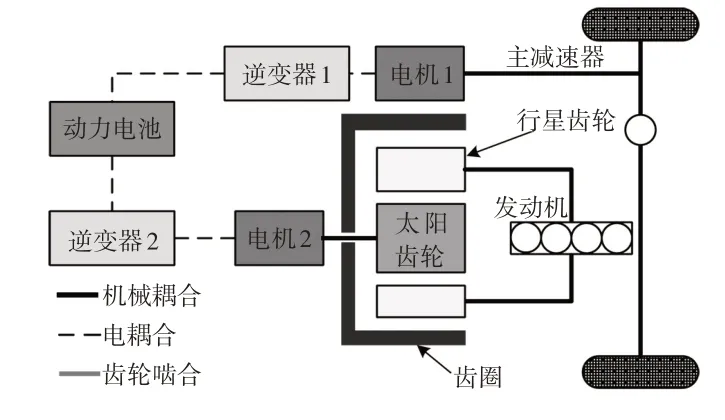
图1 动力系统结构

2.2 电机模型

基于电机转速和转矩，电机效率表示为：

式中，w(m)、Te(m)分别为第m个电机的转速、转矩；η(m)为第m个电机的运行效率；Te(m)max、Te(m)min分别为第m个电机输出的最大、最小转矩。

电机的效率MAP如图2所示。

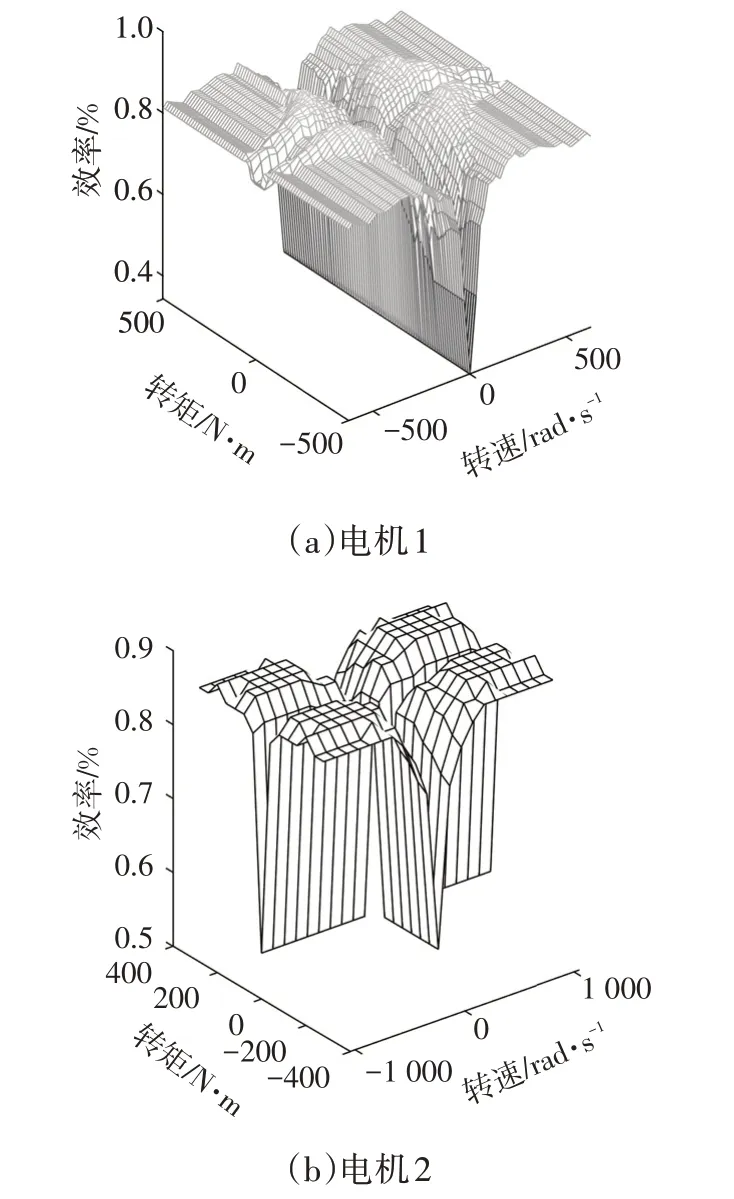
图2 电机效率MAP

2.3 发动机模型

发动机瞬时燃油消耗率mfuel可由发动机扭矩Teng和转速weng表示：

燃油消耗率MAP如图3所示，发动机最优工作曲线如图4所示，由图4可知，weng与发动机功率Peng存在对应关系，Peng=g(weng)。故根据式（2），在已知weng的条件下，利用Teng与燃油消耗率MAP即可确定车辆燃油消耗率。

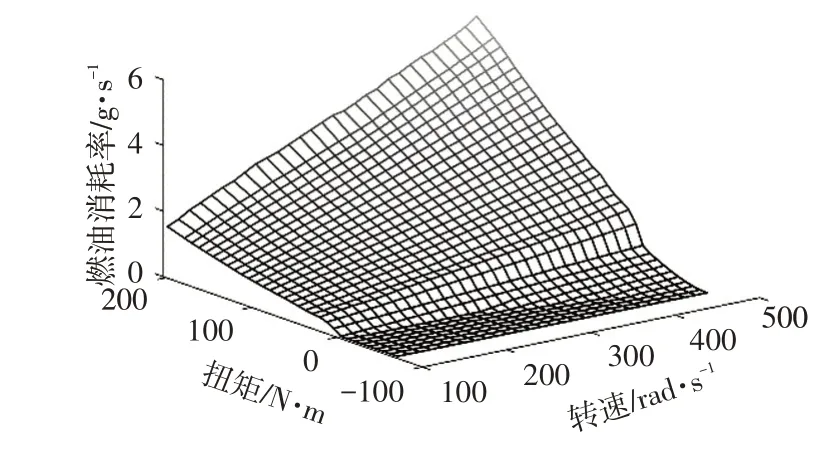
图3 燃油消耗率MAP

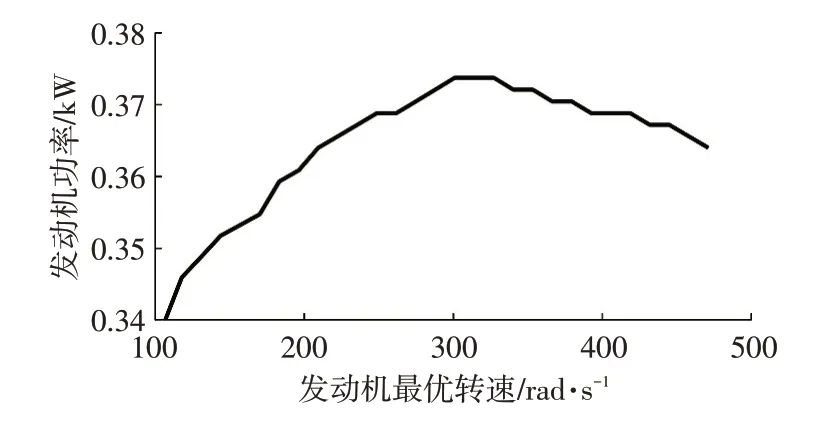
图4 最优工作曲线

2.4 电池模型

电池组采用一阶RC等效电路模型模拟。电流ib和t时刻荷电状态（State of Charge，SOC）S(t)可表示为：

式中，Pb为电池功率；Sinit为初始SOC；U为开路电压；Rb为内阻；Qb为电池容量。

利用电池放电试验可获取单体电池U和Rb随SOC的变化关系如图5所示，基于t时刻的SOC，通过插值算法可得到t时刻的U和Rb。

图5 单体电池U、Rb随SOC的变化曲线

3 速度控制器建模

3.1 队列模型

研究对象为3 辆参数相同的PHEV，其行驶场景为5辆车组成的队列，研究对象位于队列中心。行驶工况为坡度及附着系数均动态变化的高速工况。队列模型如图6 所示，道路累计坡度如图7 所示。图6 中，队列领先车辆0 在给定高速公路燃油经济性试验（Highway Fuel Economy Test，HWFET）工况的基础上加入了速度干扰，车辆4 提高行驶速度，从而缩短整个队列的间距。利用MPC 原理，基于前车的速度及整个队列的长度，以车辆间距离误差、速度误差为成本函数，实时获取车辆1～车辆3的速度，确保队列的安全行驶。

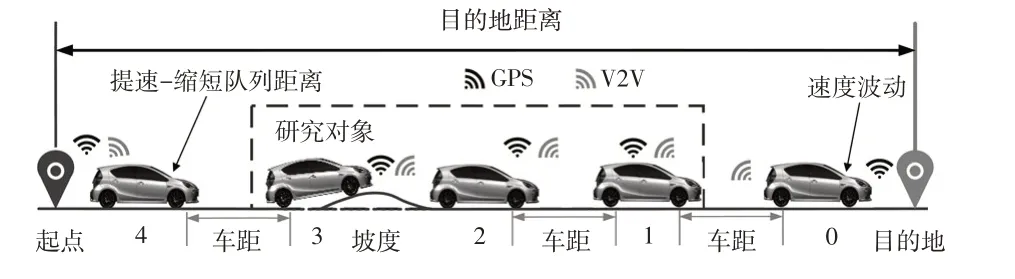
图6 队列示意

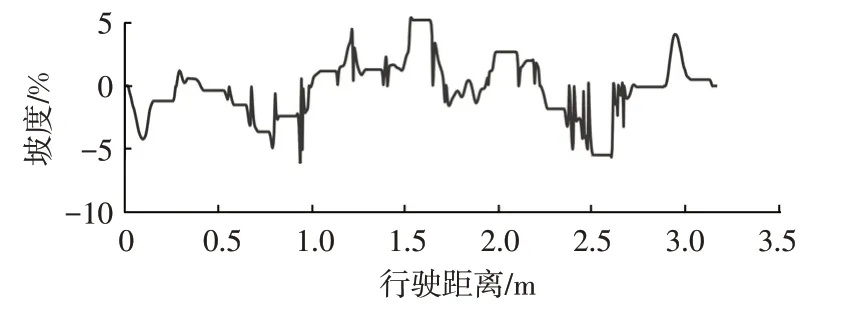
图7 道路累计坡度

假设车辆行驶于混凝土路面，考虑到路面存在泥泞或碎石等情况，该路面滚动阻力系数φ的范围为0.005～0.025[16]。设初始滚动阻力系数为0.015，其改变量Δφ的定义规则为：

式中，mod为取余函数。

车辆0在t时刻的速度为：

式中，λ为0.8～1.2 范围内的随机数；vHWFET为标准高速工况车速。

编号为n的目标车辆与其前车间动态车距ddes(n)为：

式中，d0为默认的安全距离，通常设置为5～15 m；vego(n)为队列中相邻车辆间后车n的车速，即目标车辆的车速；Thead为时间常数；dcut为后车加速行驶所缩短的队列距离：

式中，v(4)为车辆4的车速。

队列的状态变量可以表示为：

式中，d(n)为车辆n与其前车间的距离；aego(n)为车辆n的加速度。

使用t时刻车辆n的状态x(n)(t)来预测(t+1)时刻的状态x(n)(t+1)：

由当前车辆的状态x(n)(t)预测(t+k)时刻的状态x(n)(t+k)为：

对于队列里相邻车辆，可根据状态变量中的运动学参数设计MPC目标函数。t时刻编号为n车辆的目标函数J(n)(t)包括车辆间距和车速，计算公式为：

式中，Δd(n)(t)、Δv(n)(t)分别为t时刻编号为n的车辆与其前车间的距离误差、速度误差，系统需保证当Δd(t)趋近于0 时，Δv(t)和后车加速度为0；d(n)(t)为第n辆车在0～t时刻的行驶距离；ddes(n)(t)为t时刻编号为n的车辆与其前车间动态车距；v(n)(t)为t时刻编号为n的车辆速度；qd、qv分别为距离误差、车速误差的权重。

队列在运行时还应满足如下限制：

式中，Δdmax、Δdmin分别为相邻车辆间距离误差的上限和下限；Δvmax、Δvmin分别为速度误差的上限和下限；amax、amin分别为加速度的上限和下限；Δamax、Δamin分别为加速度变化的上限和下限；a(n)(t)为t时刻编号为n的车辆加速度。

3.2 径向基神经网络

RBFNN 是一种具有单隐层的3 层前向网络，分别为输入层、隐层和输出层。其学习方法与反向传播神经网络（Back Propagation Neural Network，BPNN）类似，但其隐层的激活函数与传统的神经网络层不同，可实现输入向量的线性化转换。通过合理调节权重，确保RBFNN 可以任意精度逼近非线性函数，从根本上解决了BPNN局部最优问题。

本文所设定工况中车辆0 的速度、队列距离、附着系数及坡度会实时改变，此时MPC 频繁运行调整后车加速度，确保队列安全运行，该做法会导致后车加速度波动较大。考虑到基于MPC所搭建的速度控制器是一个复杂的变参数非线性系统，而RBFNN 具有在无法获取准确数学模型的非线性系统中实现最优控制的特性，为了减少波动，提高驾驶员的驾驶体验，以车辆加速度为控制对象，建立了基于RBFNN 的速度控制器模型。首先选定目标车辆车速vego、目标车辆与其前车间速度误差Δv、目标车辆与其前车间距离差Δd作为RBFNN输入，目标车辆加速度aego作为RBFNN输出。然后基于MPC 原理，利用式（5），经过N次MPC 算法迭代，获取1～N次迭代后的[vego{1,2,…，N}Δv{1,2,…,N}Δd{1,2,…,N}]数据集和[aego{1,2,…,N}]数据集，为获取充足的训练数据集，每次迭代过程车速会调整为标准工况的0.8～1.2倍。最后通过训练输入、输出数据集，从而生成RBFNN 速度跟踪控制器应用于队列中，确保车辆以更平稳的加速度运行。RBFNN结构如图8所示。该网络含有3个隐层，并分别具有10 个神经元。图中p为输入数量，p=3；e为神经元数量；z为隐层数量；qe为第e个神经元的权重。

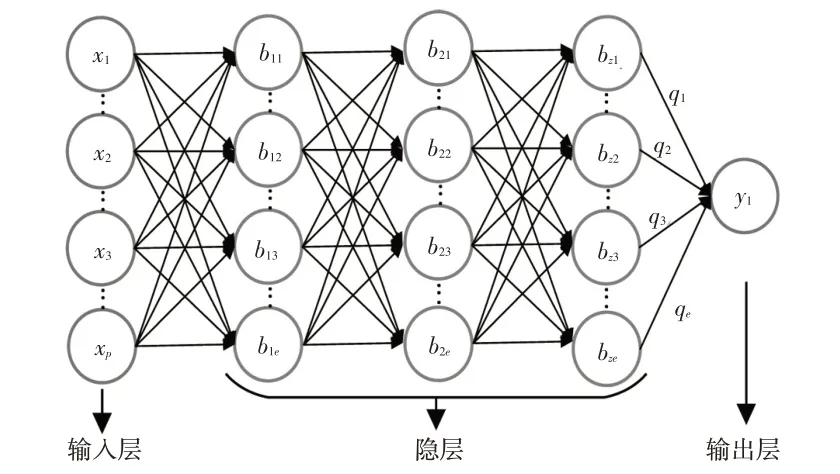
图8 RBFNN速度控制器结构

4 基于随机动态规划的能量管理策略

4.1 马尔可夫链

马尔可夫过程表示为：假设研究对象在ta时状态为Sa，在tb时处于状态Sb的可能性仅与ta时所处的状态Sa有关，即

在该过程中，研究对象从Sa至Sb的状态转移矩阵Pa,b为：

式中，D为状态数量。

所选定工况速度及车辆需求功率如图9所示。

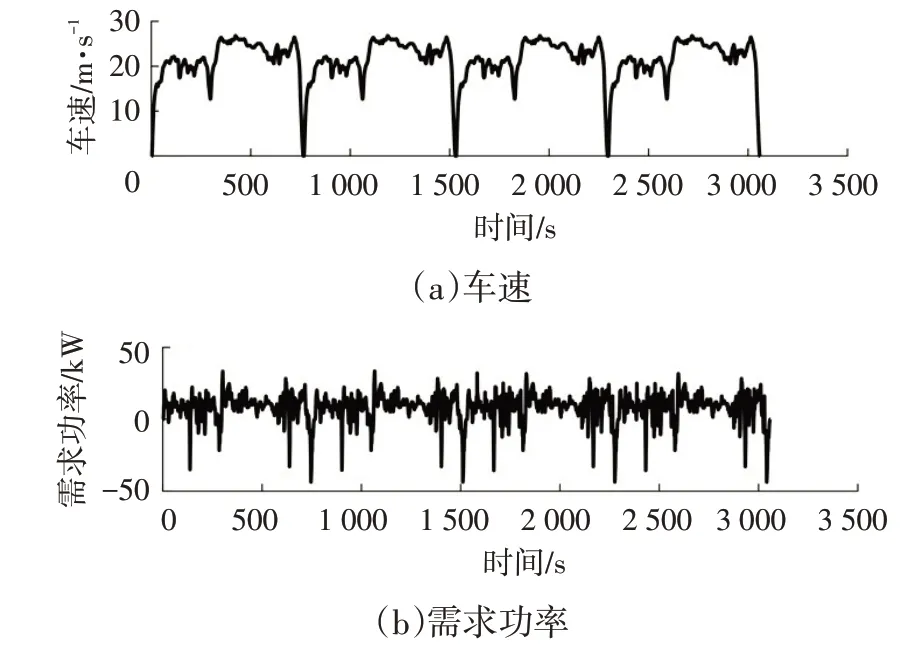
图9 工况车速及需求功率

将车速、需求功率离散化，可表示为：

式中，Nv、Nr分别为速度和需求功率离散的数量；preq为离散化的需求功率集合；v为离散化的车速集合。

基于最邻近算法和最大似然估计可得车辆以某一速度vm行驶时需求功率从Sa至Sb的概率Pa,b(vm)为：

式中，Na,b(vm)为以vm行驶时preq从preq(a)转换为preq(b)的次数；Na(vm)为以vm行驶时preq为preq(a)的次数。

以vm=25 km/h 为例，状态转移概率分布如图10 所示，由图10可得，状态转移主要发生在邻近状态间。

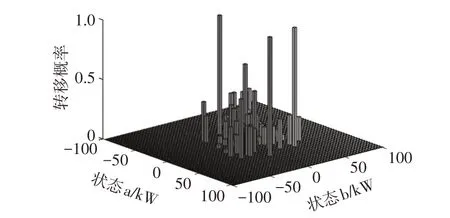
图10 状态转移概率

4.2 基于随机动态规划的能量管理策略

基于随机动态规划所搭建的能量管理策略的控制变量为电池功率pbat，状态变量为荷电状态S、车速v、需求功率preq，成本函数为油耗，即

式中，Ttotal为工况总时长。

求解SDP 问题时，若状态由a转为b，基于Bellman原理，此时状态转移的值函数（代价）为：

式中，Zk(b)为k次迭代时，状态b的值函数；β∈(0,1)为保证成本函数收敛的收敛因子；μ表示所采取的动作；Ja,b(μ)为基于动作μ，状态由a转为b时的成本函数。

从第k次到第(k+1)次迭代过程中Bellman误差为：

为了确保策略最优，Bellman误差ε须满足：

式中，∂为最大允许误差。

假设当前迭代策略为Ck，此时需基于状态-行动[(S,v,preq),(pbat)]计算Q函数值：

基于Ck时所得Q值QCk更新策略Ck+1：

由式（20）可以得到每个状态下的最优值函数，利用各状态下的最优值函数，基于贪婪策略，将其组合为全局最优策略，即

基于随机动态规划所搭建的能量管理策略具体流程如表2所示。

表2 策略迭代流程

4.3 基于规则的能量管理策略

将基于规则的能量管理策略作为对比量，该策略根据发动机的稳态效率特性确定逻辑门限参数阈值，将车辆驱动模式划分为纯电动模式、发动机模式、联合驱动模式。具体模式切换如图11所示。当发动机需求转速和需求转矩较低时，发动机效率低，此时采用纯电动工作模式，已达到节能目的。当需求转速和需求转矩提升，且处于发动机最优效率曲线内，采用发动机工作模式。当车速且需求转矩均较大时，为了确保动力，采用联合驱动工作模式。

图11 车辆驱动模式切换

4.4 分层控制策略总体框架

基于SDP 与RBFNN 结合的插电式混合动力汽车队列的分层优化控制策略总体控制框架如图12 所示。

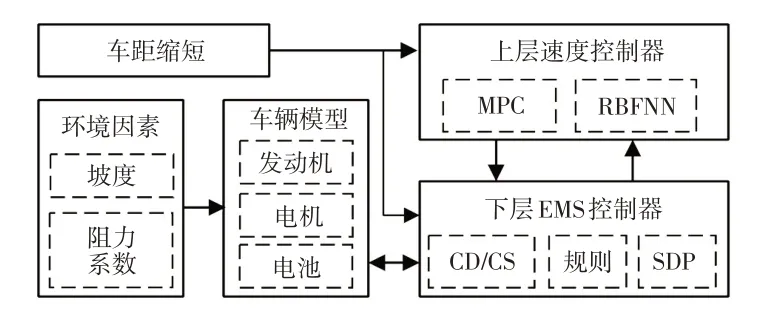
图12 总体控制框架

5 仿真结果与分析

5.1 上层速度控制器结果分析

为了验证基于RBFNN所搭建的上层速度控制器的工况适应性，队列领先车辆0 在给定参考HWFET 工况的基础上加入速度干扰，并完全遵循干扰后的HWFET驾驶循环的速度曲线行驶。车辆1～车辆4 将使用上层速度控制策略跟踪车辆0，确保队列安全行驶，车辆4在行驶时会提升车速，压缩队列距离。图13a显示了标准HWFET工况下车辆速度和加入速度干扰后车辆0的速度。以车辆2为例，运行时由于坡度和滚动阻力系数变化导致其加速度的改变量如图13c所示。

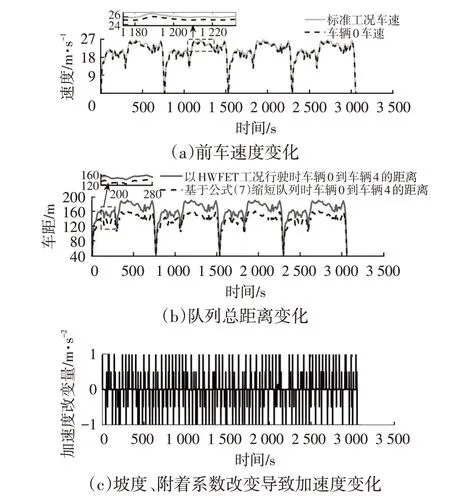
图13 队列干扰

图14a显示了车辆队列的跟随性能，当前车加速或减速时，跟随车辆表现出优异的跟踪能力，速度波动小。由图14b 可知，在指定工况场景中，车辆并未发生碰撞，且上层控制器可以通过及时调节车辆加速度，确保车辆间距的实时更改。

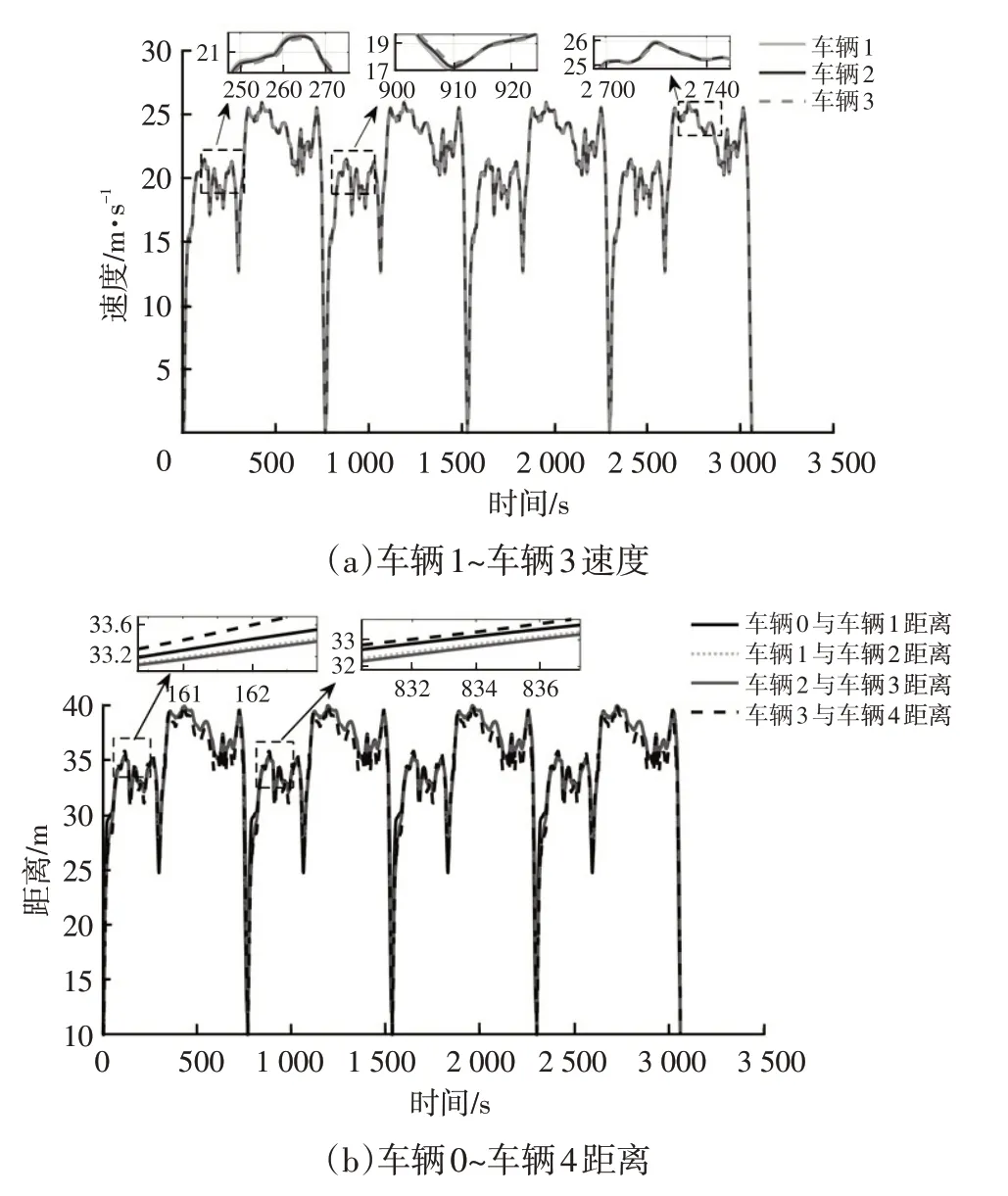
图14 车速和距离对比

由于车距、坡度、附着系数不断变化，速度控制器会频繁工作来改变车辆1～车辆3 的加速度，导致车辆1～车辆3的跟踪速度及加速度的波动较大，此时乘坐体验不佳。故利用RBFNN 优化基于MPC 所搭建的速度控制器，平滑加速度曲线。以车辆2 为例，优化后车辆间距如图15 所示，由图15 可得，相较于MPC 搭建的上层控制器，RBFNN-MPC 策略在确保车辆安全距离的同时，所得到的车辆加速度波动小，间距曲线平稳，即此时车辆不会频繁加减速，乘坐体验得到提升。

图15 神经网络训练结果对比

5.2 下层能量管理控制器结果分析

上层速度控制器在确保车辆间安全距离的同时，将车辆速度、加速度信息传递至前文动力系统模型中，从而获取不同时刻车辆SOC和preq。基于SDP的能量管理策略将获取的SOC、v、preq作为状态变量，以油耗作为成本函数，基于表2 中策略迭代步骤实时控制电池功率pbat。车辆基于SDP 训练所得策略运行时单步运行时间经计算为0.029 316 77 s，满足实时性的要求。

将基于电量消耗-电量维持（Charge Depleting/Charge Sustaining，CD/CS）策略、规则控制策略作为对比策略，基于3种策略的SOC对比结果如图16所示。由图16可知，基于CD/CS 策略，车辆均先依靠电池放电为车辆提供动能，当电池SOC 达到30%后，发动机起动并消耗燃油为电池充电。该过程相较于基于规则的控制策略、SDP策略，SOC下降速度最快，由此导致车辆后期运行时会消耗大量燃油。规则控制策略与SDP策略相比，SOC下降速度在工况前中期大体一致，但由于SDP的本质为全局最优问题求解，故其SOC下降速度最慢。

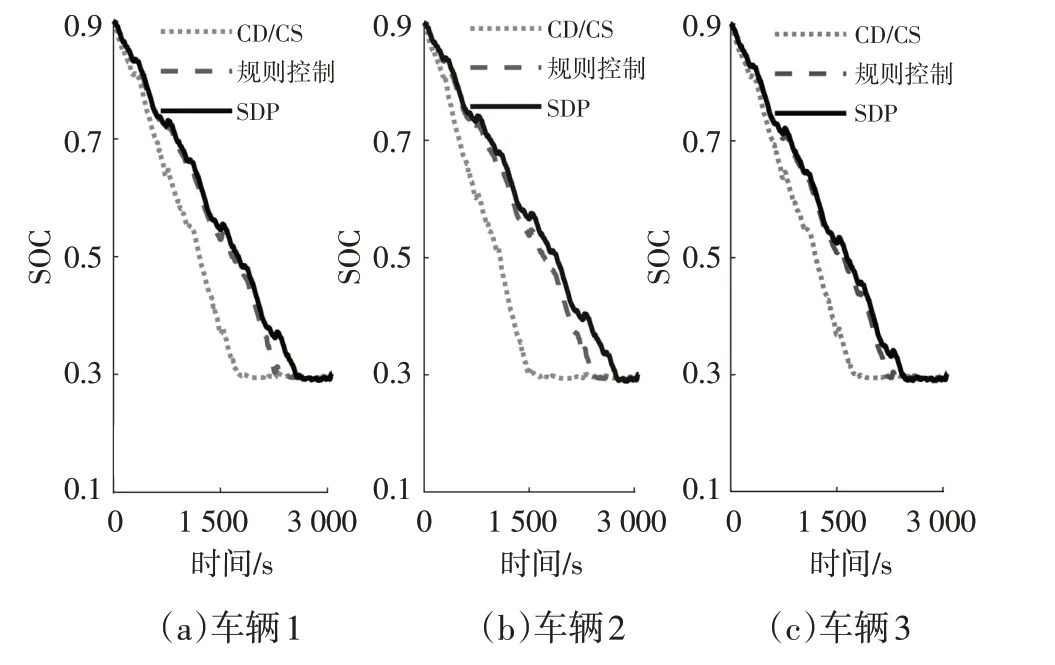
图16 基于3种策略的SOC对比结果

3 种不同策略的油耗和SOC 消耗对比结果如表3所示。发动机工作率的对比结果如图17 所示，由图17 可得，基于规则控制策略的发动机工作率略高于CD/CS 策略，SDP 策略最低。这是因为设定工况为高速工况，发动机的需求转矩、需求转速相较于城区工况更大，鉴于规则策略的原理，此时车辆处于发动机模式及联合驱动模式的次数会增加。CD/CS 策略中SOC 低于30%后，发动机会频繁起停为电池充电，从而驱动车辆行驶。故整体而言，SDP 策略发动机工作率最低。

表3 3种策略能耗对比

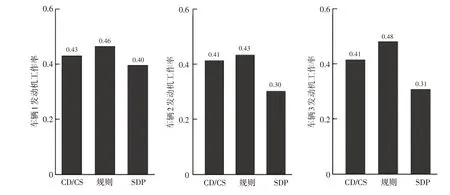
图17 发动机工作率对比

图18 所示为3 辆车基于不同策略时发动机工作点对比结果，由图18可得，车辆以CD/CS策略运行时发动机工作点大部分处于25%以下的低效率区域，此时发动机常以低转速、低转矩状态运行。当车辆以规则控制策略和SDP 策略运行时，发动机大部分工作于25%～30%的效率区域。SDP策略相较于规则控制策略，发动机的工作点更靠近高效率区。

6 结束语

本文以插电式混合动力汽车队列模型为研究对象，提出了一种分层优化控制策略。该策略上层搭建了基于RBFNN 的速度控制器，下层提出了基于SDP 的能量管理策略。仿真结果表明，在高速工况下，所提出的上层速度控制策略相较于MPC控制，加速度变化更平缓，乘坐舒适性好。下层提出的SDP 策略与CD/CS 策略及规则控制策略相比，队列中车辆油耗及发动机工作率均有所降低。综上所述，所提出的基于RBFNN 与SDP 结合的插电式混合汽车队列的分层优化控制策略具有一定的有效性和可行性，可为后续研究提供参考。