基于规则约束的深度强化学习智能车辆高速路场景下行驶决策*

王新凯 王树凤 王世皓

（1.山东科技大学，青岛 266590；2.山东五征集团有限公司，日照 262306）

主题词：深度强化学习 行驶决策 智能车辆 规则约束 改进DQN算法

1 前言

行驶决策是智能驾驶的核心技术，也是目前的研究热点之一。行驶决策算法主要分为基于规则的算法和基于机器学习的算法[1-2]。

基于规则的行驶决策算法模型主要有有限状态机[3]、模糊逻辑模型[4]等，规则类算法的可解释性好，但无法处理较为复杂和随机的动态道路场景，每添加一条规则，都需要考虑与规则库中的其他规则是否存在冲突。

基于机器学习的换道决策算法模型主要有决策树模型[5]、深度学习模型[6]、强化学习模型[7-9]等。随着深度学习与强化学习的迅速发展，基于机器学习的算法在行驶决策算法中所占比重不断增加。

文献[5]使用随机森林和决策树对数据集进行分析，并输出决策结果，但算法对数据集的依赖性强，数据中的噪声会直接影响算法的准确性。文献[6]设计了基于长短时记忆（Long Short-Term Memory，LSTM）神经网络的端到端决策算法，但算法缺少探索能力且存在“黑箱”问题，可解释性差。强化学习克服了决策树模型和深度学习模型依赖人工标注数据的问题，通过与环境的交互学习最优策略，为复杂交通环境下的决策提供了新的解决思路。文献[7]使用DQN 完成高速公路场景下的端到端自动驾驶决策，并在部分路段达到了人类驾驶员水准。文献[8]使用深度确定策略梯度（Deep Deterministic Policy Gradient，DDPG）算法建立了连续型动作输出的端到端驾驶决策，在开放式赛车模拟器（The Open Racing Car Simulator，TORCS）平台上进行验证。文献[9]使用NGSIM（Next Generation Simulation）数据集搭建高速路场景，并采用竞争网络（Dueling Network）、优先经验回放等方式对DQN 网络进行了改进。但DQN 算法存在随机性强、收敛速度慢等不可避免的缺陷。

为更好地解决强化学习算法下智能车辆训练过程中的动作选择随机性强、训练效率低等问题，本文提出一种基于规则约束的DQN 智能车辆行驶决策模型。DQN 算法输出智能车辆的行驶决策，基于最小安全距离与可变车头时距的动作检测模块实现对DQN动作的硬约束，将规则引入奖励函数实现对智能车辆的软约束，同时结合对算法结构的改进，实现智能车辆安全高效的驾驶行为。

2 强化学习原理

2.1 DQN算法

DQN 是在Q-Learning 算法的基础上演变而来，利用深度卷积神经网络代替Q-Learning的表格解决“维度灾难”问题，实现了连续状态空间下强化学习的应用。

首先，DQN算法基于ε-贪心（ε-greedy）的探索策略与环境进行交互。Q 估计网络对Q值（从某个动作出发，到最终状态时获得奖励总和的奖励期望）进行估计，并选择Q值最大的动作输出，在更新一定次数后，再将评估网络参数的权重复制给Q目标网络，Q目标网络负责目标值yt的计算。通过最小化损失函数L(θ)来更新Q估计网络。算法的整体框架如图1所示。

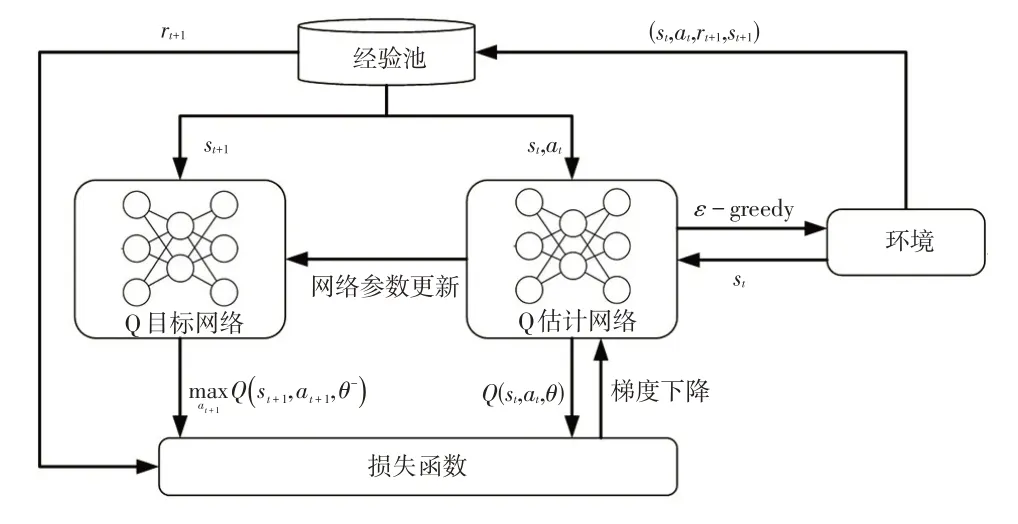
图1 DQN整体框架

DQN目标值的计算公式为：

式中，yt为t时刻目标值；rt+1为(t+1)时刻获得的瞬时奖励；γ为折扣系数，可调节未来奖励对当前动作的影响；Q(st+1,at+1,θ-)为Q目标网络对状态st+1所有下一步动作at+1的Q值估计；θ-为Q目标网络的参数。

DQN的损失函数为：

式中，Q(st,at,θ)为Q估计网络对状态st和动作at的Q值估计；θ为Q估计网络的参数；E为求期望操作。

2.2 DQN算法的改进

DQN 算法在实际应用中存在着过估计、更新效率低、Q值估计不准确等问题，针对以上问题，本文分别采用双重深度Q 网络（Double DQN）、竞争深度Q 网络（Dueling DQN）、N 步深度Q 网络（N-Step DQN）对原始的DQN 算法进行改进。将结合竞争网络和双重网络（Double Network）的DQN 变体称为D3QN，将引入NStep学习的D3QN称为ND3QN。

2.2.1 双重深度Q网络

DQN 算法对Q值的估计和最大Q值动作的选择均在Q 估计网络中完成，存在过度估计的问题，使得估计值大于真实值，可能导致次优动作的Q值大于最优动作的Q值，算法收敛到局部最优。

Double DQN[10]针对DQN 过度估计的问题，将动作的选择和评估过程进行了解耦。Q估计网络选择动作，Q目标网络拟合当前动作的Q值。

Double DQN目标值的计算公式为：

2.2.2 竞争深度Q网络

DQN算法不同动作对应的Q值需要单独学习，无法更新相同状态下的其他动作。同时在Highway-env环境的某些状态下，Q值的大小与当前状态有着直接的联系。

Dueling DQN[11]对网络的结构进行了改进，将其分为2个部分，将信息先分流到2个支路中：一路代表状态值函数V(s)，表示环境状态本身具有的价值；另一路代表当前状态下的动作优势函数A(s,a)，表示选择某个动作额外带来的价值。最后将这2 个支路聚合得到Q值。同时，Dueling DQN 中限制同一状态下动作优势函数A(a)的平均值为0，这意味着当前状态的某个动作对应的Q值更新时，其他动作的Q值也会进行更新，将大幅提高算法的训练效率。

竞争网络结构目标值的计算公式为：

式中，β为状态值函数独有部分的网络参数；α为动作优势函数独有部分的网络参数；为所有可能采取的动作；A为动作空间的维数。

2.2.3 N步深度Q网络原始DQN 采用了单步时序差分方法，需要后一步的单个即时收益和状态对当前状态进行更新。蒙特卡洛方法（Monte Carlo Method）则必须采样到终止状态才能更新对应状态价值，只有走完完整的仿真步长才能更新Q值。N-step DQN[12]则是这2 种方法的折中，向后采样的时间步长n灵活可变，在训练前期对目标价值可以估计得更准确，从而加快训练速度。

步长n截断后目标值的计算公式为：

3 基于规则约束的DQN

为了减少智能车辆训练过程中无意义的碰撞，将规则引入深度强化学习算法，在保证智能车辆合理探索区间的前提下，减少训练过程中的危险动作。将引入的规则分为与换道相关的硬约束和与车道保持相关的软约束，分别通过动作检测模块与奖励函数实现。

3.1 基于规则约束的DQN整体构架

基于规则约束的DQN整体构架如图2所示，所用仿真环境是Highway-env平台中的高速路场景。

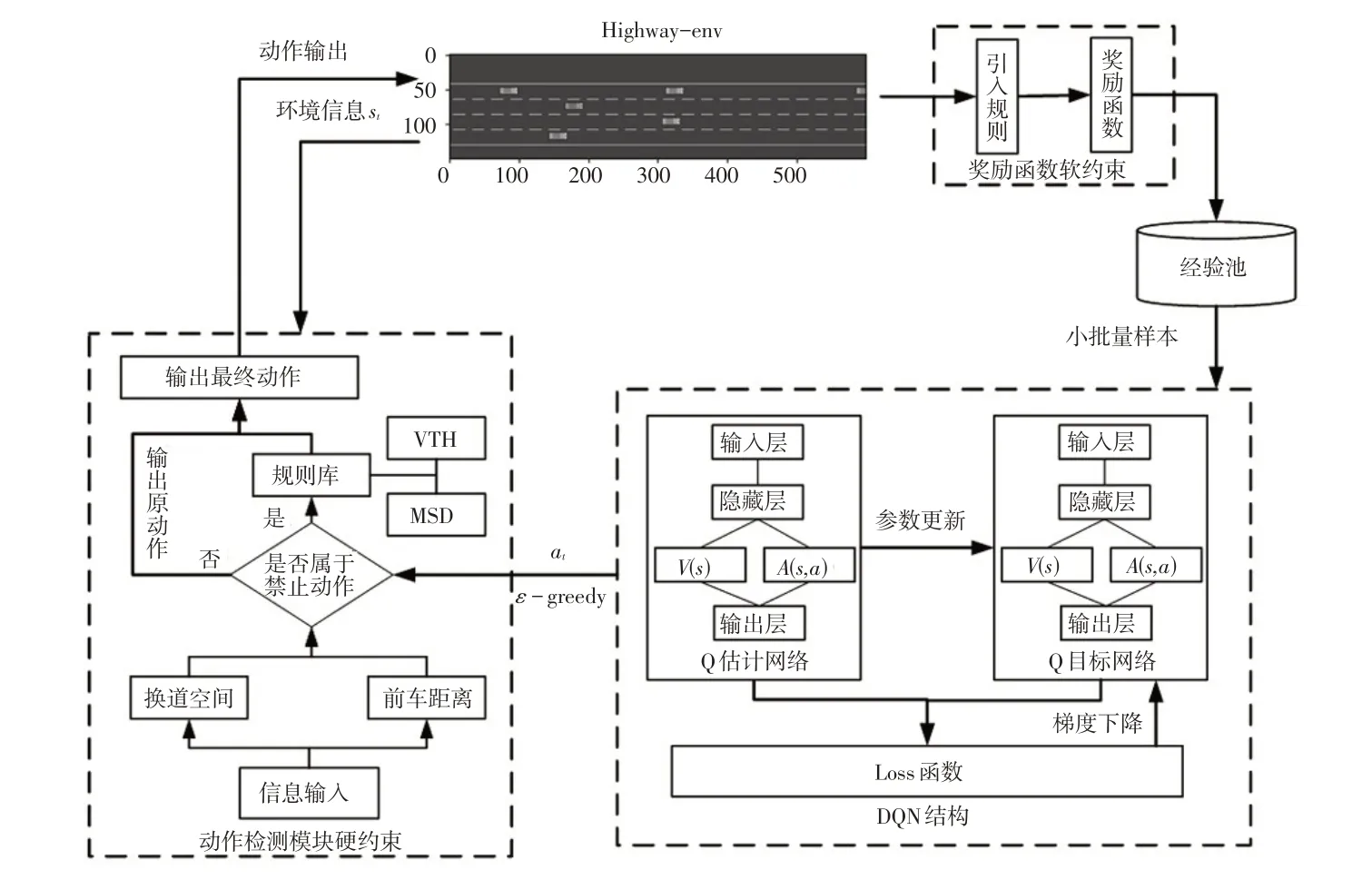
图2 基于规则约束的DQN整体构架

与DQN 普通构架相比，基于规则约束的DQN 构架主要增加了动作检测模型，并将规则分为硬约束和软约束分别加入动作检测模型和奖励函数中。

在行驶过程中，智能车辆首先获取自身和周围车辆的参数信息作为当前时刻的状态值，同时将动作值、奖励值、下一时刻的状态值作为一个元组存储到经验池，从中抽取样本，并将状态值分别输入到Q 估计网络和Q 目标网络中。算法输出动作at，动作检测模块获得输出动作at和环境反馈的状态空间信息st后，对属于规则库中的危险动作进行剔除并重新输出动作决策。深度强化学习通过动作与环境的交互获得即时奖励并对损失函数进行计算，进而更新网络参数，直到算法完成迭代。

3.2 动作检测模块

基于规则库建立的规则算法可以实现智能车辆的自动驾驶，但是其设计和验证难度随着场景复杂度的提高不断增加。在遵守交通法规和符合日常驾驶习惯的基础上，可通过一系列简单的规则建立动作检测模块，以改善DQN 驾驶决策的性能，提升智能车辆在高速路场景下的行驶安全性和通行效率。

动作检测模块主要由换道最小安全距离（Minimum Safety Distance，MSD）理论[13]和可变车头时距（Variable Time Headway，VTH）模型[14]建立。换道最小安全距离即保证换道安全而两车之间必须保持的最小行车间距。最小安全间距策略具有计算速度快、结构简单的优点。可变车头时距模型可以根据自车车速、相对车速等因素对跟车间距进行调整，可实现对可行性、安全性、灵活性的综合考虑。

换道最小安全距离模型应用场景如图3所示，其中Lo为当前车道的前车，Ld为相邻车道的前车，Fo为相邻车道的后车，M 为换道车辆，而车辆M 的车速大于当前车道后车的车速，所以忽略当前车道后车。

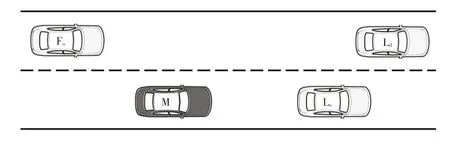
图3 基于最小安全距离的换道场景

换道最小安全距离为：

式中，W为车辆宽度；Gmin为换道结束后两车的车头间距；φ为换道中换道车辆与车道线所成的夹角；Di为换道过程中车辆i的纵向位移。

可变车头时距安全距离为：

式中，v为智能车辆自车速度；d0为最小车间距，指自车停车时车辆前端与前车末端的间距；Th为可变车头时距参数。

可变车头时距参数Th的计算公式为：

式中，Th_max、Th_min分别为可变车头时距参数设置的最大、最小值；kr为相对车速的系数；vr为自车与前车的相对车速；t0为自车与前车的车头时距。

动作检测模块对当前状态空间信息st进行处理得到前车车距与换道空间信息，根据最小安全距离和可变车头时距对DQN 算法输出的动作at进行检测，禁止导致碰撞的危险动作，并输出当前环境下的最优或次优动作，所遵循的规则如表1所示。

表1 主要来源于对日常驾驶习惯的总结及动作检测模块所需要完成任务的理解。在高速路场景中，智能车辆主要面临换道与跟驰这2种决策任务，因此分别在动作检测中引入换道最小安全距离和可变车头时距这2 种对应规则模型，对智能车辆输出的动作进行筛选。同时，车辆驾驶可以解耦为纵向和侧向2 个方向，可变车头时距的约束范围为纵向，换道最小安全距离的约束范围为纵向和横向。纵向约束上采用与前车的车距作为指标，而在与前车接近的过程中，智能车首先受到可变车头时距模型作用，然后受到换道最小安全距离模型影响。侧向约束只受换道最小安全距离模型的影响。

表1 中的前2 条主要对智能车辆的无意义换道（即智能车辆执行换道指令必然导致碰撞）进行约束，避免由换道引发的碰撞。第3条、第4条主要对智能车辆的跟随与换道决策进行判断，当前车已经小于跟随距离但还存在换道空间时，车辆继续直行保持车速或加速的行为是明显错误的，需要换道。第5条只是对智能车辆在训练过程的随机行为进行屏蔽，即使碰撞不可避免，但加速行为依然是明显错误的。需要说明的是，规则表并不是为了完全避免碰撞，而是通过简单明了的规则约束来减少智能车辆在训练中的无效输出与探索。

3.3 奖励函数的设置

深度强化学习通过智能车辆与环境的不断交互产生数据，通过迭代学习到相应环境下的最佳策略。奖励函数的设置对深度强化学习有至关重要的影响，智能车辆通过累计奖励（Reward）达到最大来判断当前的策略是否为最佳策略。仿真平台中的高速路场景中默认奖励函数考虑的因素较少，不利于算法的训练。

3.3.1 原奖励函数分析

原环境中奖励函数主要由以下2个部分组成：

a.车速奖励。鼓励智能车辆以较高车速行驶，车速奖励函数为：

式中，vmin为智能车辆的最小速度；vmax为车道限制的最大速度。

b.碰撞惩罚。对智能车辆与其他车辆发生碰撞的情况进行惩罚，其数值为：

原环境中奖励函数公式为：

式中，wv、wc为各项权重系数，原奖励函数的各权重设置为0.4、1；Normal为归一化函数，将奖励函数输出范围线性变换至[0,1]。

在实际应用中发现，该奖励函数在探索中对碰撞不敏感，输出减速动作的频率低，更倾向于追求高车速而导致碰撞发生。因为奖励归一化的原因，智能车辆以最低速度行驶在车道上就将得到较高的单步奖励，在个别情况下智能车辆将学到以最低车速坚持到整个回合结束的极端保守行为决策。

3.3.2 修改后的奖励函数分析

针对原奖励函数存在的问题，将相对车速与相对距离等因素加入奖励函数，提高碰撞时的扣分值，并取消奖励的归一化操作，提高智能车辆对前车车距的敏感性，加快智能车辆训练进程：

a.车距惩罚。通过VTH、MSD、相对车速对智能车辆与前车的车距给出反馈，其奖励函数为：

其中，Df为车距系数：

式中，vf为前车车速；d为智能车辆与前车的车距。

b.车道奖励。鼓励智能车辆行驶在与前车碰撞时间（Time to Collision，TTC）最大的车道上，当所在车道为智能车辆与前车的TTC 最大的车道时，其奖励函数为：

c.换道惩罚。车辆行驶过程中应避免频繁变速换道，以保证乘员乘坐舒适性，换道惩罚项为：

综上，修改后的综合奖励函数为：

式中，wv、wc、wT、wlc、wd为各项权重系数。

4 仿真分析

4.1 仿真参数与环境设置

为了验证基于规则约束的DQN 算法的有效性，选取Highway-env 中的高速路场景搭建仿真环境，将基于规则约束的DQN 算法应用于智能车辆驾驶行为决策，验证算法在典型交通场景中的有效性和收敛速度，并与原始DQN算法进行对比。

仿真环境如下：CPU 为Inter Core i5-10400，内存为16 GB，GPU为NVIDIA GTX 2080，深度强化学习编译框架为Pytorch。根据车辆决策的适用场景和需求，设置Highway-env 的环境为单向4 车道场景，各车道从左到右的编号分别为0、1、2、3，场景中的其他车辆的数量为30 辆，其他车辆由最小化变道引起的总制动（Minimizing Overall Braking Induced By Lane Change，MOBIL）和智能驾驶员模型（Intelligent Driver Model，IDM）进行横、纵向控制，高速路环境的各参数如表2所示。

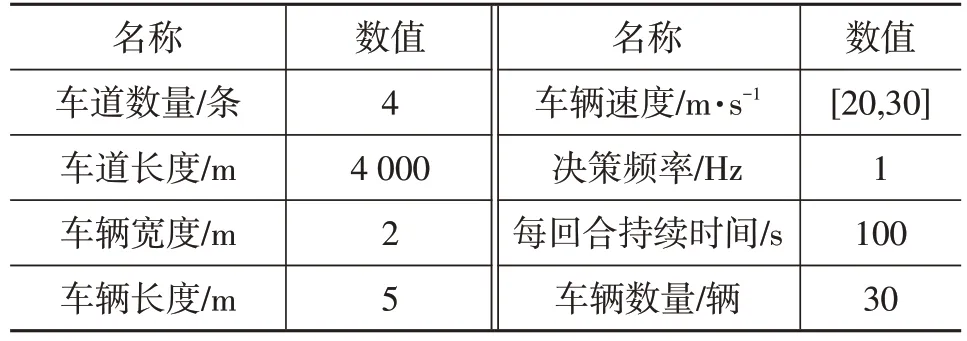
表2 高速路环境的各参数

智能车辆在高速环境中的动作有5种，分别为左转向、保持、右转向、加速、减速，对应动作空间为[a0,a1,a2,a3,a4]。

DQN算法各超参数设置如表3所示。

表3 DQN算法超参数设置

4.2 奖励函数分析设置

在原奖励函数的基础上，修改后的新奖励函数经多次仿真验证后，各权重取值为0.4、5.0、1.0、1.0、1.0。统一用DQN 算法在不同奖励函数下训练12 000 回合，结果如表4所示。

表4 不同奖励函数测试结果

从表4中可以看出：DQN在采用原奖励函数时的表现不佳，即使通过12 000回合训练，成功率仅为3.53%；修改奖励函数后，再次训练DQN 的成功率达到了33.16%，碰撞次数下降了30.71%，在新奖励函数车距惩罚的影响下，智能车辆跟驰行为所占的时间增加，车速有所下降。以上结果表明，奖励函数的设置对深度强化学习表现有着直接的影响，修改后的奖励函数大幅提高了智能车辆与前车保持车距的能力。

4.3 对仿真结果的对比分析

将测试中所有深度强化学习算法训练到完全收敛并达到最佳水平，所花时间很长，以原奖励函数下的DQN为例，算法在训练27 400回合后，成功率曲线依然有缓慢上升的趋势，时间成本较高。因此受时间成本影响，在仿真分析时，统一训练12 000回合。同时，深度强化学习输出数据具有波动性，为使输出结果更加直观，对深度强化学习输出的速度、位移、回报值等数据均使用Python内置库中的Savitzky-Golay滤波器进行平滑处理。Savitzky-Golay 滤波器能够在不改变信号趋势的情况下进行数据的平滑处理。

4.3.1 原奖励函数下不同算法对比分析

原奖励函数下，不同算法的成功率、单回合平均车速、单回合平均行驶距离、单回合累计回报值，如图4～图7所示。

图4 不同算法在原奖励函数下的成功率

图6 不同算法在原奖励函数下的单回合平均行驶距离

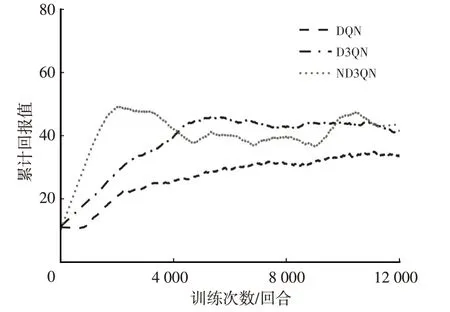
图7 不同算法在原奖励函数下的单回合累计回报值

不同算法在环境原奖励函数下的各项测试结果如表5所示。

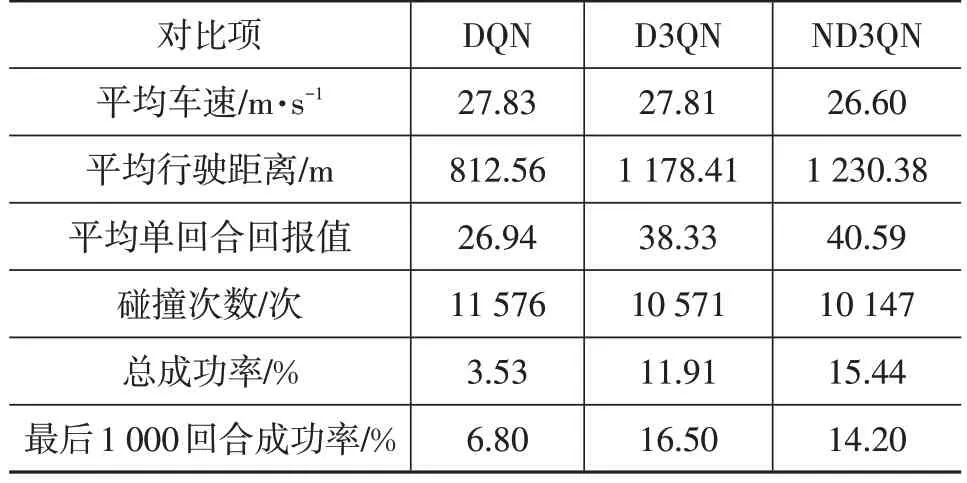
表5 不同算法在原奖励函数下测试结果

由表5 可以看出，即使未改动奖励函数，得益于网络结构的改进，D3QN 算法也表现出更高的学习效率，成功率达到了11.91%。ND3QN算法在引入多步学习能力后，通过对Q值的更精准估计，在前2 000 回合的表现即超过了D3QN 算法12 000 回合训练的效果，但在4 000 回合后成功率出现了一定下降，虽然在总成功率上超过了D3QN 算法，但在最后1 000 回合成功率低于D3QN算法。

深度强化学习的目标是获得最大累计奖励，进一步结合各对比图可以看出，ND3QN 算法的平均车速在4 000 回合附近出现了大幅提高，但单回合的累计回报值下降并不剧烈，之后随着平均车速的小幅提升，回报值出现波动。综上，可以得出ND3QN 算法成功率出现下滑的原因是，算法采用累计回报值作为学习目标而不是成功率，ND3QN算法优先稳定车速，通过增大平均行驶距离来提升累计回报值，平均行驶距离达到稳定后，提高平均车速来增加自己的单步奖励。提高车速后，原低速状态下的车间距在高车速下将不再安全，ND3QN算法的碰撞次数增加，成功率出现下滑。ND3QN 算法训练过程成功率的下滑也再次从侧面证明了原奖励函数的不合理之处。

4.3.2 动作检测模块与新奖励函数影响分析

在使用原始DQN 算法的情况下，分别引入动作检测模块与新奖励函数，将引入动作检测模块的DQN 算法称为动作检测深度Q 学习（Action Detection Module DQN，ADQN），新奖励函数下的DQN函数记为R+DQN，完全引入规则约束的DQN算法记为规则约束深度Q学习（Rule Constrained DQN，RCDQN）。引入不同修改项后算法的成功率、单回合平均车速等信息如图8 和表6所示。

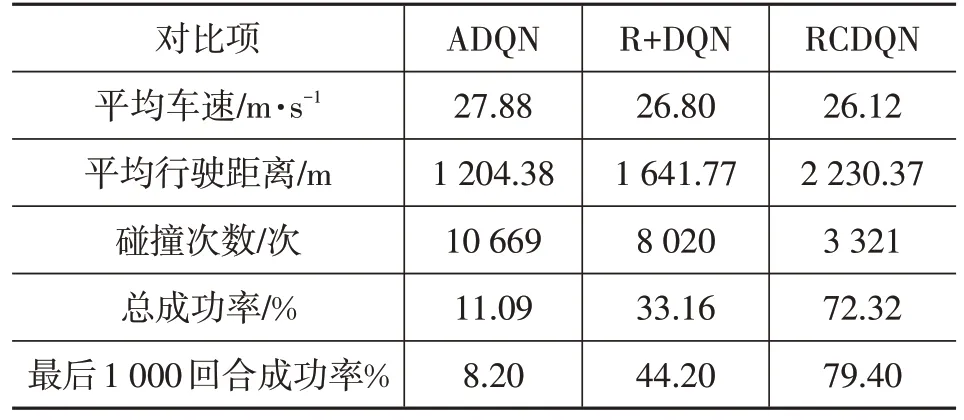
表6 DQN算法引入动作检测模块与新奖励函数测试结果

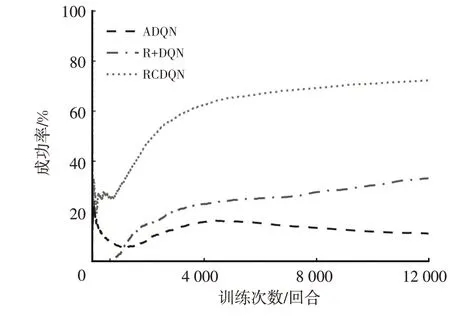
图8 DQN算法添加不同修改项后的成功率

由图8 可知：动作检测模块在训练的初期（即平均车速处于低速区段时）能够减少智能车辆的碰撞；训练1 000回合后，引入新奖励函数的DQN算法的成功率超过了ADQN，与前车保持车距的能力则成为了智能车辆成功的关键；将动作检测模块和修改后的奖励函数结合后，智能车辆在训练中成功率得到了大幅提升，成功率达到了72.32%。

4.3.3 引入规则约束框架后各算法对比分析

在统一使用动作检测与新奖励函数的规则约束框架（Rule Constrained）情况下，分别对DQN、D3QN、ND3QN 算法表现进行分析，规则约束框架下各算法的成功率、单回合平均车速等信息如图9和表7所示。

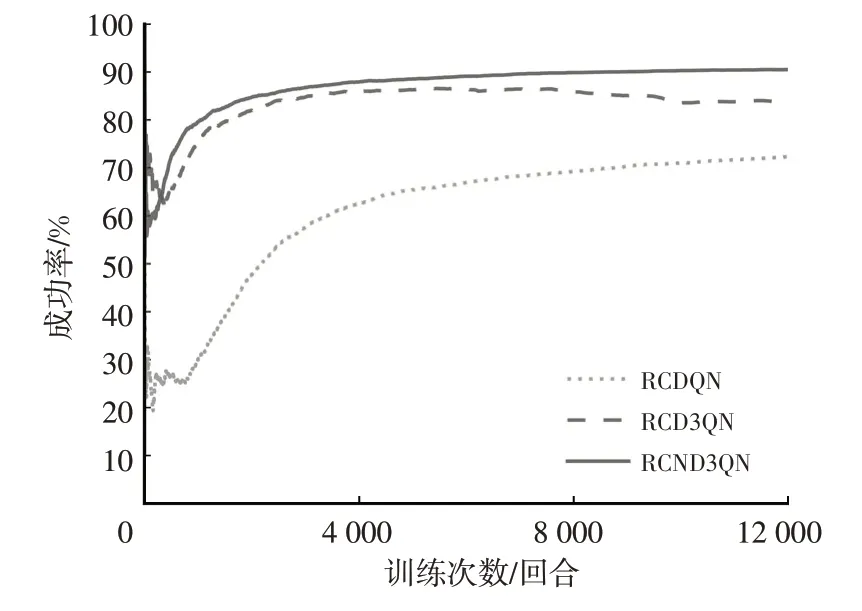
图9 规则约束框架下各算法成功率

结合图9 和表7 可得，引入规则约束框架的各算法的平均车速随着算法改进程度的提高而依次降低，成功率随着算法改进程度的提高而增大，RCND3QN 算法总成功率达到了90.51%，比RCDQN 算法提高出了18.19百分点，表明在算法的改进将进一步提高智能车辆性能的上限，而规则约束框架的引入提高了智能车辆性能的下限。

4.3.4 智能车辆行驶过程分析

以RCND3QN算法为例，对算法在10 000回合时的部分关键帧进行分析，关键帧如图10所示。

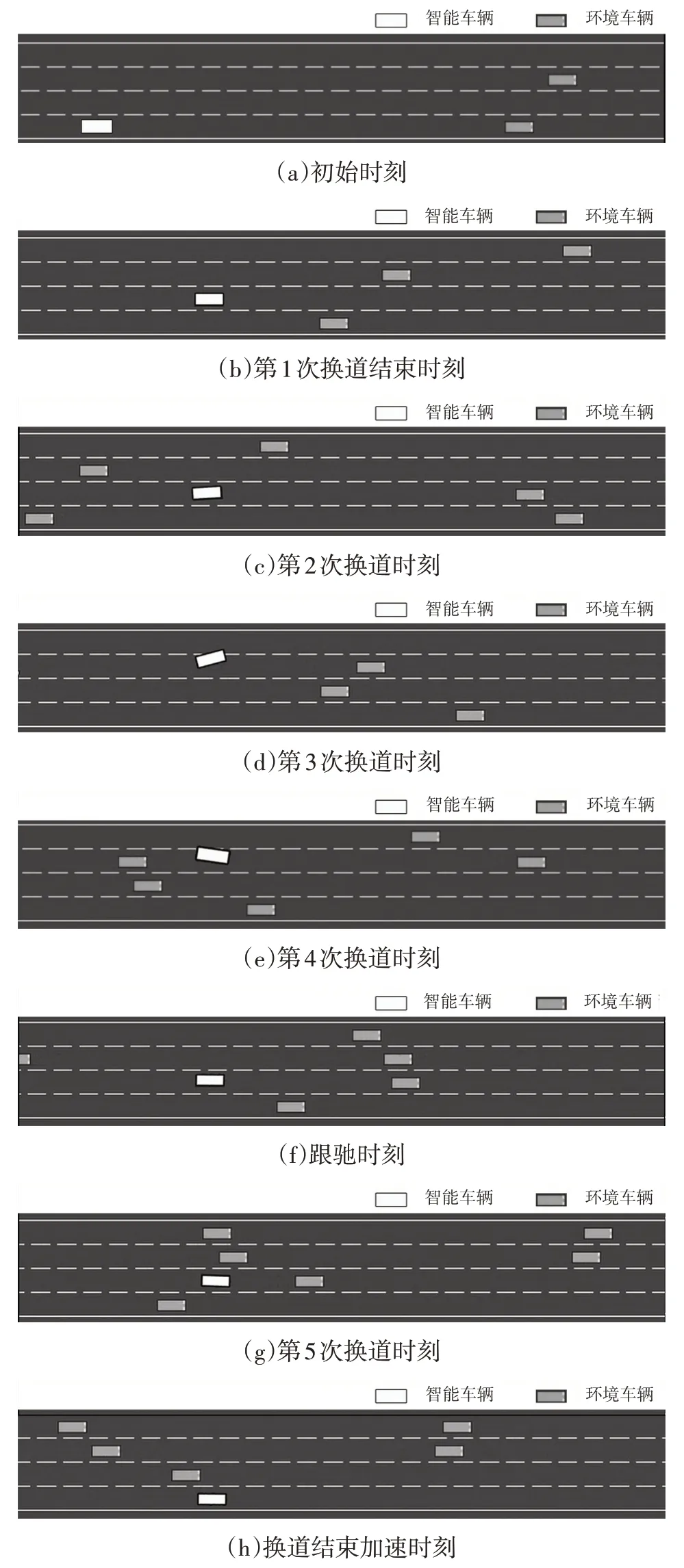
图10 规则约束框架下ND3QN算法行为决策

由图10可知：初始时刻，智能车辆车速为25 m/s，由所在第4 车道转向空旷的第3 车道；第1 次换道结束时刻，智能车辆在第3 车道由25 m/s 加速至27.5 m/s；第2次换道时刻，智能车辆预见到在第3 车道的障碍车后，由第3车道转至第2车道；第3次换道时刻，智能车辆减速至25 m/s并由所在第2车道转向空旷的第1车道；第4次换道时刻，智能车辆在行驶中逐渐左转进入第2 车道；跟驰时刻，智能车辆减速至22.5 m/s 与前车保持车距，等待时机；第5次换道时刻，智能车辆判断第3车道的车间距满足换道条件，准备由第3车道转向第4车道；换道结束加速时刻，智能车辆转移至第4 车道，开始重新加速，由22.5 m/s加速至30 m/s。

5 结束语

针对智能车辆决策问题，本文在保证智能车辆合理探索区间的前提下，使用规则对DQN 算法的输出进行约束，并对算法结构进行了改进，仿真结果表明：

a.在引入Dueling-DQN、Double DQN、N-step DQN对算法进行改进后，更改结构后算法的表现优于原始DQN。

b.算法分别通过动作检测模块与修改奖励函数来实现规则约束，仅引入单一改进项时修改奖励函数的提升大于动作检测模块，但引入完整规则约束框架后智能车辆在训练中成功率远超两者单独作用的线性相加之和。

c.算法的改进将进一步提高智能车辆决策性能的上限，而规则约束框架的引入提高了智能车辆决策性能的下限。

同时研究也存在以下不足：

a.规则框架中的硬约束对DQN 算法干预比较粗糙，仅仅是初步的引入，没有将规则与算法进行深入融合。

b.受限于时间成本，算法参数并没有调整至最佳，仅根据经验进行了粗略的调整，算法成功率与实际应用的要求差距较大，仍有继续上升的空间。