基于响应面模型的汽车气动特性优化*
查银龙 张扬 刘学龙 刘海 王刚
(1.河北工业大学,天津 300401;2.中汽研(天津)汽车工程研究院有限公司,天津 300300)
主题词:气动特性 风洞试验 响应面模型 遗传算法
1 前言
汽车气动阻力影响燃油经济性,气动升力影响操纵稳定性[1],侧风工况下产生的气动侧向力易导致侧滑、横摆甚至侧翻等危险情况发生。汽车高速行驶状态下,受外界风的干扰更为敏感,改善气动特性可提高汽车的综合性能。一般通过汽车改型来优化气动特性,需要经历建模、网格划分、仿真计算等过程,耗费资源多、周期长,并且很难控制3个气动力系数同时达到最优[2]。如何提高汽车气动特性优化的效率,平衡所有气动力系数的优化效果成为一大难题。
为此,很多研究人员以单个或多个气动力系数为目标,集成汽车外形优化设计所需的多项技术,来改善气动特性。李壮[3]以降低气动阻力为目标,借助Isight优化软件,优化了某SUV的12个造型参数,获得了很好的减阻效果。张英朝等[4]结合参数化软件与计算流体力学(Computational Fluid Dynamics,CFD)软件,确定了某载货汽车的8 个优化设计变量,使气动阻力系数降低10.4%。张勇等[5]通过封闭前部底盘,增加附加装置并进行优化,使升力系数降低36.4%。陆润明等[6]结合多岛遗传算法,通过优化侧围、侧窗及门槛等,降低了气动侧力系数。然而,上述研究主要是对单个气动力系数的优化,未实现汽车气动特性的综合改善,因此,还需进行多个气动力系数的优化研究。刘欢等[7]基于modeFRONTIER优化平台,利用智能算法使Ahmed模型的气动阻力及升力系数同时得到优化。亓昌等[2]考虑了气动阻力系数和侧力系数,对MIRA标准模型进行多目标优化,获得最优解集并确定了3种典型优化方案。但以上优化过程未同时考虑3个气动力系数,可能出现一个气动力系数改善,其他气动力系数恶化的情况。
本文综合考虑气动力系数的优化效果,在风洞试验验证仿真模型的基础上,探究不同侧风工况下气动力系数的变化规律,以某侧风工况为基准进行气动特性优化设计。对汽车进行参数化建模,以造型参数作为输入,在参数取值范围内使用均匀拉丁超立方抽取样本点,进行流场计算,输出气动力系数,建立近似输入与输出关系的响应面模型,利用多目标遗传算法进行全局寻优,获得Pareto前沿最优解集。
2 模型构建与试验证验
2.1 无侧风工况的仿真模型构建
为使用数值模拟法研究侧风角对汽车气动特性的影响,首先建立汽车无侧风工况的数值仿真模型,借助试验,验证模型的可靠性。汽车车速较低,周围流场压强变化小,故外流场可视为不可压缩流场[8],其连续性方程和动量守恒方程分别为:
式中,xi为i方向的位移;ui为i方向速度分量;t为时间;ρ为气体密度;P为静压力;Tij为应力张量;Si为i方向广义源项。
按照1∶1的比例对某车型进行几何建模,该车型长4.3 m、宽1.765 m、高1.585 m,清理汽车表面,封闭格栅,保留汽车底盘、机舱等细节,如图1所示。

图1 汽车几何表面
建立长52 m、宽20 m、高12 m 的计算域,如图2 所示。汽车几何的正投影面积为2.370 3 m2,计算域入口面积约为240 m2,阻塞比约为0.988%,小于5%,满足阻塞比要求[9]。
图2 仿真模型的计算域
计算域的边界条件设置如表1所示。
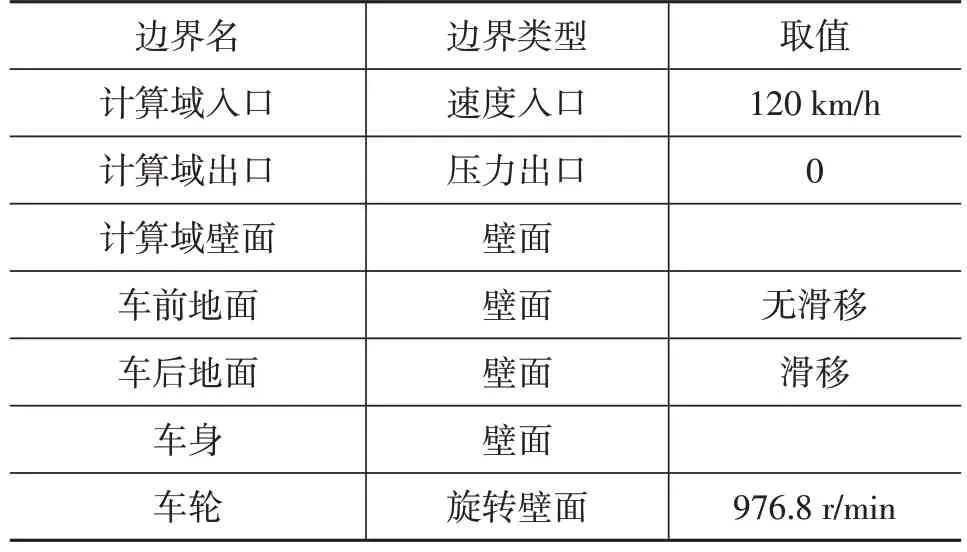
表1 边界条件
为提高车身周围的计算精度,设置2 个加密层,网格截面如图3所示。
图3 汽车对称面网格截面
利用相关参数计算雷诺数,结果为:
式中,ρ=1.184 15 kg/m3;l=2.6 m 为轴距;ν∞=33.33 m/s 为相对速度;μ=1.855 08×10-5N·s/m2为动力黏度系数。
雷诺数远大于4 000,属于湍流问题[10],采用间接数值模拟雷诺时均法,应用布辛涅司克(Boussinesq)假设使方程封闭。为使仿真计算获得更好的精度,选择带旋流修正的Realizablek-ε模型[11],湍流动能k及耗散率ε方程分别为:
式中,μt为湍流黏度;C1=max[0.43,η/(η+5)]、η=Sk/ε为系数;C2、C1ε、C3ε为常量;v为动力黏度;为表面张力系数;Sij=(∂uj/∂xi+∂ui/∂xj)/2为平均张量旋率;Pb为浮力产生的湍流动能;Pk为层流速度梯度产生的湍流动能;σε、σk为湍流普朗特数(Prandtl)数;Sε、Sk为用户自定义的源项。
通过STAR-CCM+监测仿真模型的气动力,并计算气动阻力系数Cd,以便与试验结果对比:
式中,Fd为气动阻力;A为正投影面积。
2.2 仿真结果
图4、图5 所示分别为汽车对称位置的速度截面以及表面压力分布情况[12],可以看出:
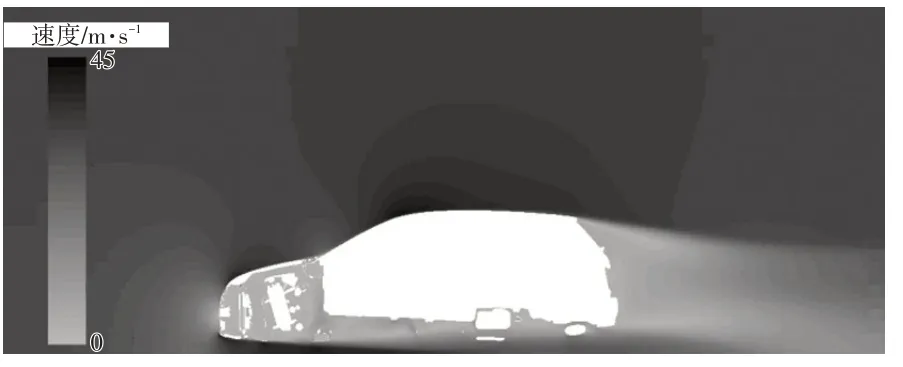
图4 汽车速度截面

图5 汽车表面压力
a.由于格栅封闭,气流撞击汽车前部形成低速区,进而产生高压。汽车机舱流入空气极少,速度极低,可以忽略,外部气流会产生分离,分别向汽车上方、底部以及车身两侧流动。
b.汽车前格栅周围、A 柱、后视镜、D 柱、后扰流板以及后尾灯等均为负压区。
c.汽车整体表面压力基本对称,车头与后端存在明显压力差,阻碍汽车行驶,两侧压力相同,无侧向力。
在无侧风工况下行驶,汽车主要受气动阻力影响,通过仿真模拟,得到汽车气动阻力系数Cd=0.326 3。
2.3 风洞试验方案
2.3.1 试验设备
通过风洞试验与上述数值模拟结果进行对比,如图6 所示,以试验作为补充,验证模型的可靠性。试验在中汽研(天津)汽车工程研究院有限公司气动-声学风洞实验室进行,此风洞为回流式、3/4 开放式风洞,喷口面积28 m2,最大风速250 km/h,温度控制在23~25 ℃,实验室满足测试条件。

图6 汽车风洞试验
2.3.2 仿真模型的试验验证
调节配重改变车身姿态,调整试验车位置,开启试验设备进行检查,确保无异常状态。为观察车速、格栅开闭以及路面模拟对气动阻力系数的影响,进行6种工况的风洞试验。其中,第6 种工况与上述仿真条件一致。利用测力天平获得气动力,扫描测量车辆正投影面积,通过式(6)计算气动力阻力系数,试验结果如表2所示。与第6种工况的试验结果对比,数值模拟的误差为5.26%,小于10%,验证了仿真模型的可靠性,证明可通过此仿真模型进行汽车气动特性研究。
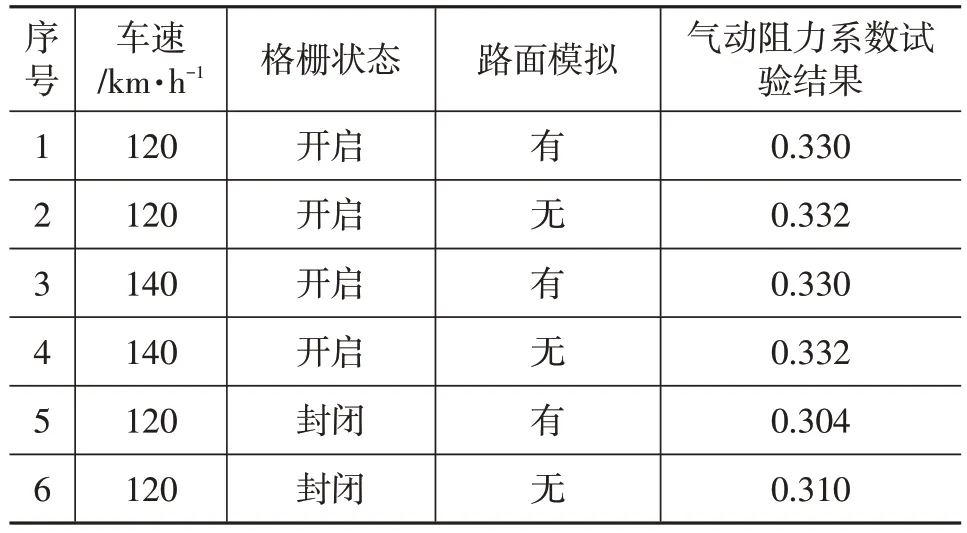
表2 试验结果
3 侧风工况下的汽车气动特性
3.1 侧风边界加载
在验证仿真模型可靠性的基础上,通过数值仿真探究不同横摆角对汽车气动特性的影响。由于上述仿真模型格栅封闭,内流场影响极小,可忽略不计,故去除机舱、平铺底盘,简化原始汽车几何,以节约计算资源,如图7所示。
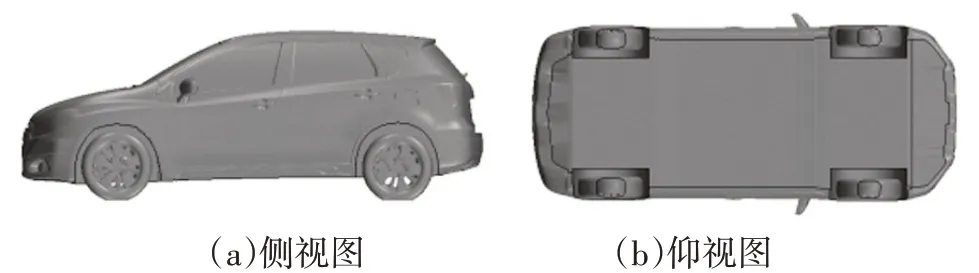
图7 简化的汽车几何表面
由于横摆角不为0°,为避免计算域过小干扰流场,将计算域的左侧边界与汽车的距离加长至15 倍车宽,并将速度入口设在左侧,右侧设为压力出口,其他条件均保持不变,利用合成速度法进行侧风加载。横摆角从-6°到15°,每隔3°设置一种工况,具体如表3所示。
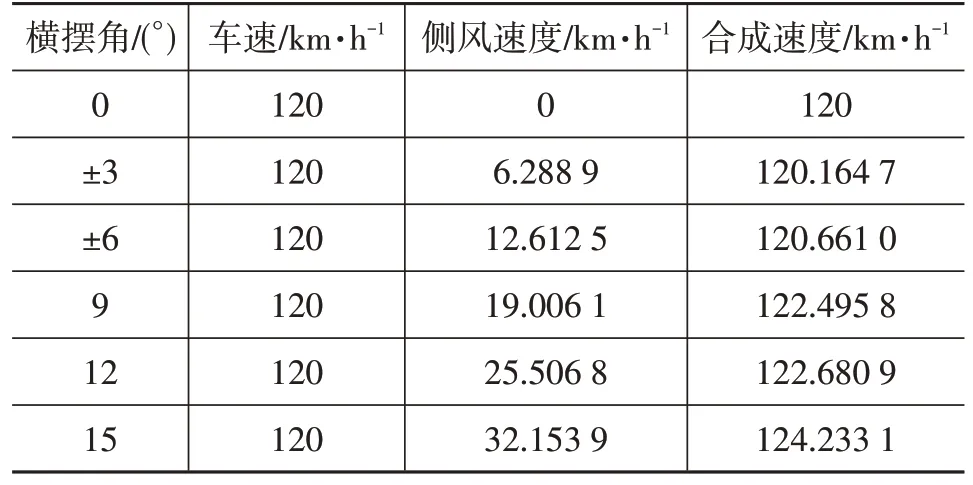
表3 侧风工况
3.2 汽车表面压力分析
通过仿真模拟,得到不同工况下的汽车迎风侧表面压力如图8所示,可以看出:


图8 侧风工况汽车压力表面
a.横摆角为0°时,正压区主要分布在车辆的正前部,汽车表面压力对称,两侧基本不存在压力差;横摆角±3°与±6°工况下,正压区域偏移方向相反。
b.在横摆角非0°的工况下,汽车迎风侧的负压区减小,背风侧的负压区增大,两侧压差增大,正压区域较大且出现偏移,横摆角越大,正压区偏移越明显,气动侧向力越大。
c.横摆角越大,压力峰值越大,汽车前端正压区域越大,气动阻力增加;随横摆角的增大,车顶表面压力也逐渐趋于负压力,汽车升力有增大的趋势。
可见在侧风工况下,流场失去对称性,随横摆角的增大,汽车的气动侧力增幅尤为明显,影响驾驶安全性。综合考虑气动力系数,对汽车外形进行优化,可改善汽车气动特性。
3.3 汽车气动力系数分析
不同工况下的气动力系数结果及变化趋势如图9所示,可以看出:横摆角为0°时,存在气动阻力,而侧力系数接近于0,随着横摆角的增大,除升力系数稍有波动外,气动力系数基本呈上升趋势;横摆角3°与-3°的工况(±6°工况类似),气动阻力系数、升力系数基本一致,气动侧力系数的数值大小接近,方向相反;横摆角从0°到15°的工况,气动侧力系数较阻力系数及升力系数的增幅均更大。
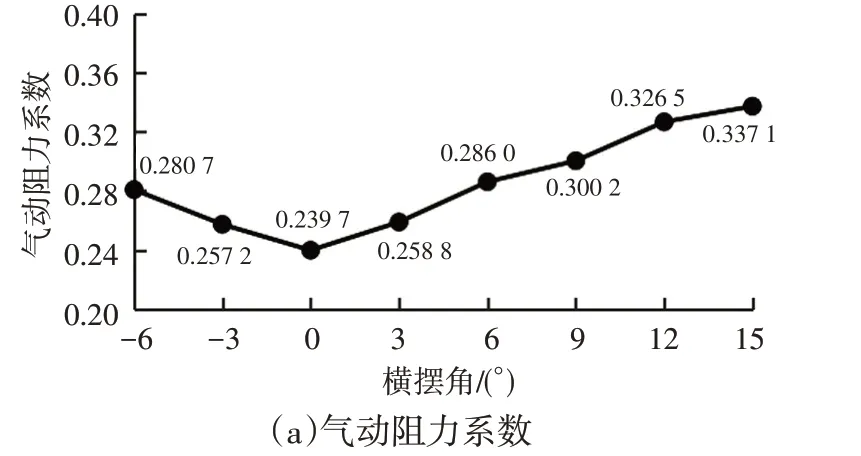
图9 不同工况下的气动力系数
因汽车两侧并非绝对对称,横摆角相反的工况下,气动力系数存在较小差别。横摆角增大,会导致汽车的气动力系数恶化,其中对气动侧力系数的影响最大。气动阻力系数增加,影响燃油经济性;升力系数的增加会降低汽车轮胎的附着力;气动侧力的增大影响汽车的行驶稳定性。故选择存在横摆角的工况,对气动力系数进行优化,降低气动力对汽车行驶的影响。
4 多目标优化设计
4.1 汽车气动特性优化
研究发现,横摆角增大,会导致气动力系数增大,进而降低汽车的综合性能,故基于某侧风工况进行汽车气动特性优化。以横摆角12°工况为例,综合考虑气动阻力系数、侧力系数、升力系数,平衡气动力系数的优化效果,对后扰流板、D柱以及后尾灯等部位进行优化,改善汽车的气动特性。
为实现高效的汽车外形优化,借助软件mode-FRONTIER 优化平台,以所选造型参数作为输入变量,通过改变输入值控制汽车几何表面变形,使用均匀拉丁超立方抽取样本点,进行仿真计算可获得输出目标。响应面模型近似输入与输出的关系,可用有限数量的样本点较准确地预测响应变量,提高优化效率。在保证响应面模型精度的基础上,选择遗传算法全局寻优,生成Pareto前沿解集。具体操作过程如图10所示。
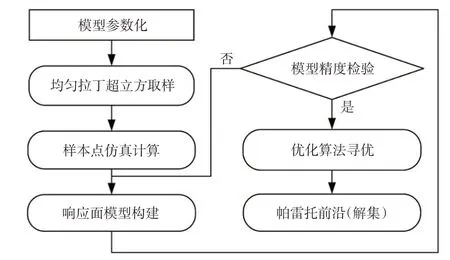
图10 优化操作流程
4.2 参数化与试验设计
为方便汽车改型,首先对车辆进行参数化建模,选取后扰流板z方向和x方向的长度变量X1、X2,D 柱的延伸量X3,以及后尾灯突出部分的长度变量X4为设计变量。定义模型原始位置参数为0,借助控制点,改变参数的大小即可改变汽车几何的外形。设计变量的取值范围如表4所示,位置及方向如图11所示。
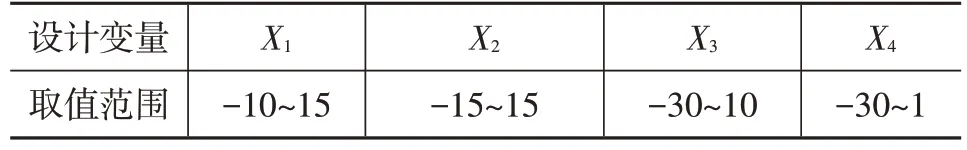
表4 设计变量取值范围 mm
使用均匀拉丁超立方法[13],抽取30组试验设计样本点。通过Java 脚本文件,调用STAR-CCM+对所选样本点进行流场计算,以计算得到的气动力系数作为输出。以横摆角12°的气动力参数为约束上限,使气动阻力系数、侧力系数最小化,升力系数也得到一定程度的减小。
4.3 参数分析与响应面模型
基于样本点的计算结果,生成如图12 所示的输入变量与输出变量的相关系数矩阵。通过该矩阵进行参数敏感性分析,可判断各输入变量对输出量的影响程度,为构建响应面模型提供参考。

图12 参数敏感性分析
由图12可以看出:后尾灯与侧力系数Cs呈负相关、与阻力系数Cd及升力系数Cl呈正相关;D 柱、后扰流板与阻力系数及升力系数呈负相关,与侧力系数呈正相关;侧力系数与阻力系数、升力系数呈负相关,升力系数与阻力系数呈正相关。
通过回归系数R2进行精度检验,最终选择精度较好的各向异性克里金(Anisotropic Kriging)法对气动阻力系数进行响应面模型构建,回归曲线如图13 所示,回归系数R2=0.944。使用径向基函数(Radial Basis Function,RBF)对气动侧力系数、升力系数进行响应面模型构建,回归曲线如图14、图15 所示,回归系数R2分别为0.906、0.996,均在0.9以上,精度满足要求。
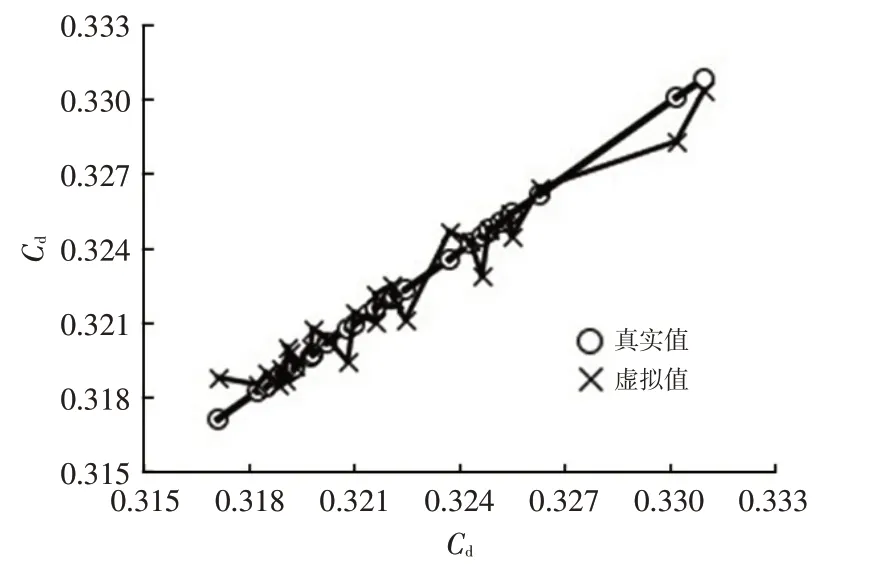
图13 阻力系数各向异性克里金回归曲线
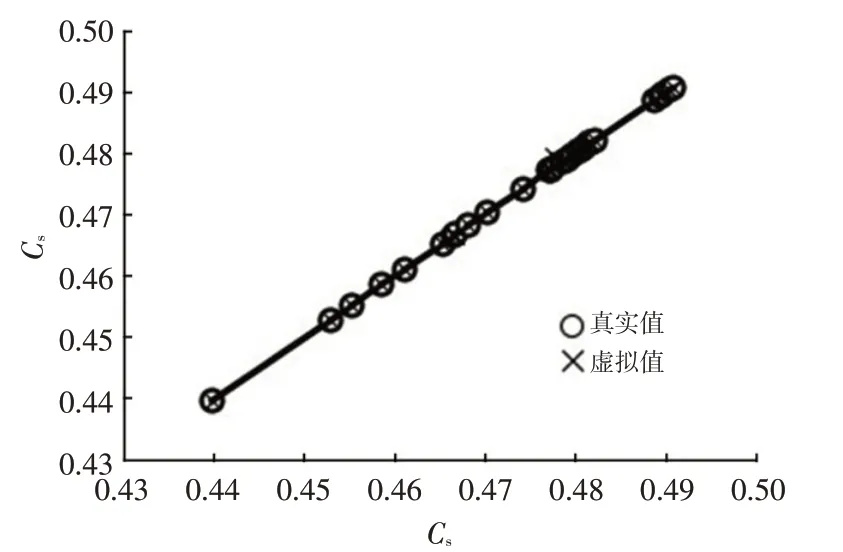
图14 侧力系数RBF回归曲线
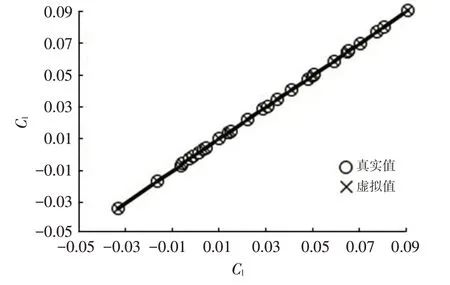
图15 升力系数RBF回归曲线
4.4 优化结果分析
基于建立的响应面模型,选用非支配排序的多目标遗传算法[14]进行全局寻优,以样本点的计算结果作为初始种群,迭代4 000次后,得到如图16所示的Pareto前沿解集。图16a 中阻力系数Cd与升力系数Cl结点分布大体呈正相关;由图16b、图16c 可以看出,侧力系数Cs与气动阻力系数、升力系数矛盾,Cs得到改善,会导致Cd、Cl变差,优化目标不协同,与参数分析结果一致。
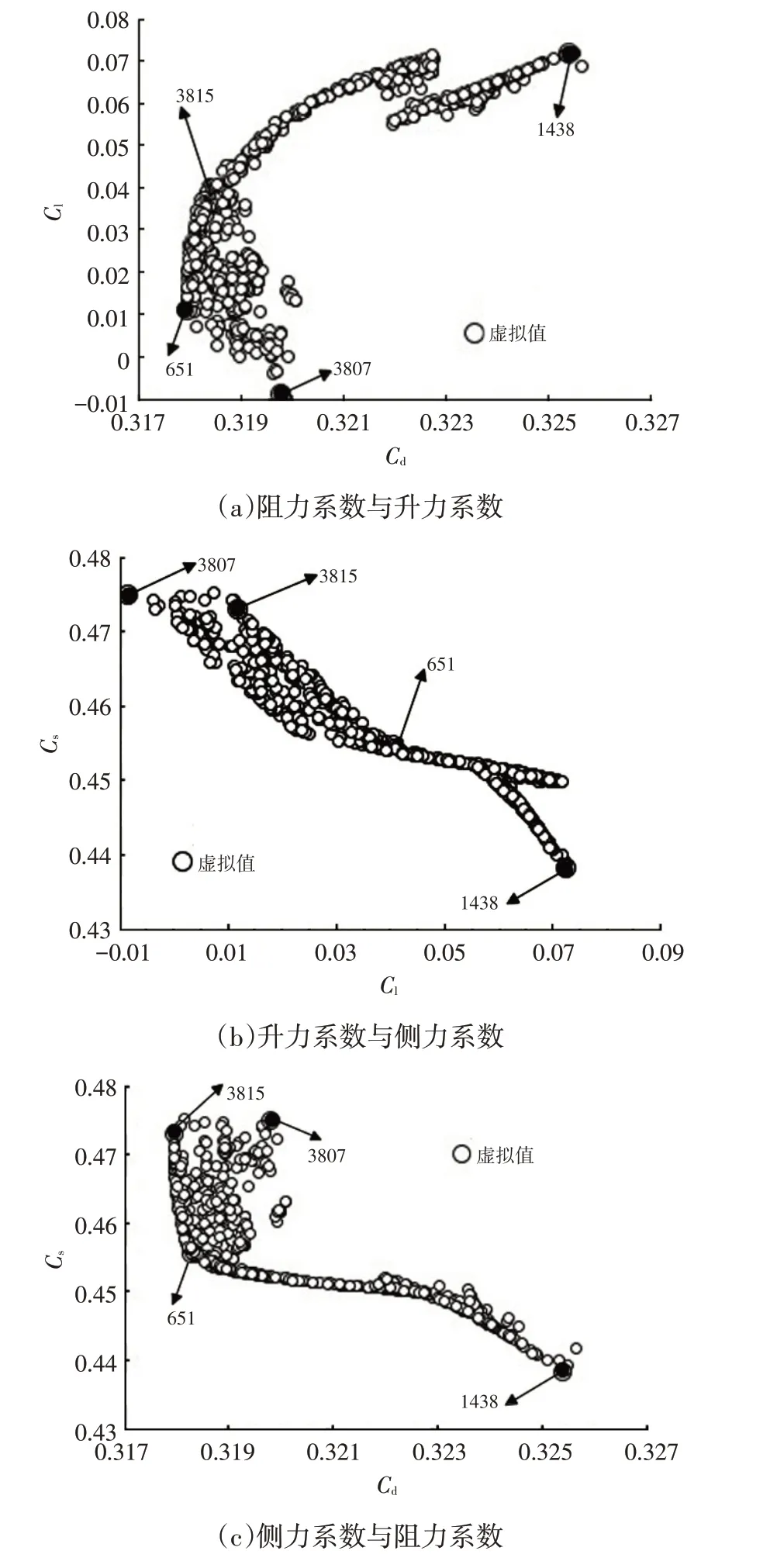
图16 Pareto前沿解集
参考基准横摆角12°工况下的气动力系数Cd=0.326 5,Cs=0.469 1,Cl=0.058 0。在最优解集中,结点气动力系数比参考基准小,则可认定为有效优化。在图16中选取最优解进行标号,确定了4种较好的优化方案。
优化方案1:标号3185,Cd=0.317 9,Cs=0.473 0,Cl=0.011 5。该方案升力系数大幅改善,侧力系数与基准相比稍差,气动阻力系数降低最多约2.63%,可改善汽车的燃油经济性[1]。
优化方案2:标号3807,Cd=0.319 7,Cs=0.475 0,Cl=-0.008 5。气动阻力系数降低约2.1%,气动侧力系数最差,升力系数减小为负值,但接近于0,升力系数的适当降低,提高了操纵稳定性[5]。
优化方案3:标号1438,Cd=0.325 3,Cs=0.438 4,Cl=0.072 0。气动阻力基本与基准一致,气动升力系数最差,侧力系数降低最多达6.54%,改善了气动稳定性[4]。
优化方案4:标号651,Cd=0.318 2,Cs=0.455 6,Cl=0.037 1。各项气动力系数均低于基准,Cd降低2.54%,Cs降低2.87%,Cl也有所降低,但均未达到最大程度的减小,此方案属于折衷解。
以上优化方案所对应的设计变量取值如表5所示,可根据实际工程要求以及设计规范,以Pareto前沿解集为参考,选取汽车外形的设计方案。
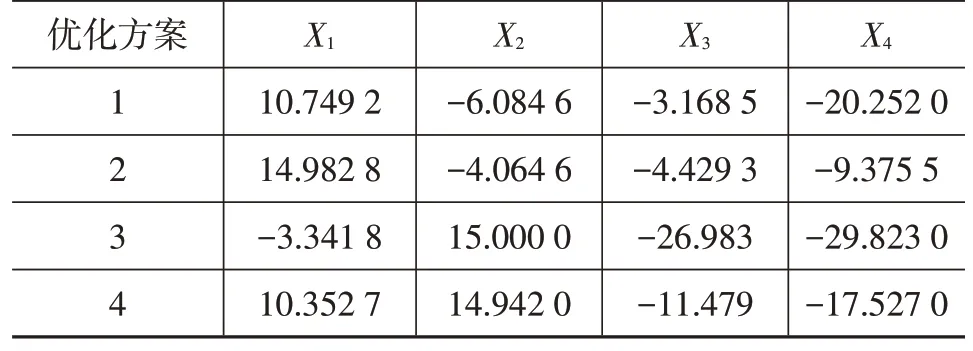
表5 优化方案设计变量 mm
5 结束语
本文以某车型为研究对象,在验证仿真模型精度及可靠性的基础上,利用简化模型探究了不同横摆角下气动力系数的变化规律,以3个气动力系数为目标进行汽车外形优化,改善汽车的气动特性,研究结果如下:
a.应用Realizablek-ε模型进行数值仿真模拟,与试验结果的误差为5.26%,验证了仿真模型的精度及可靠性。
b.不同侧风工况下,横摆角越大,汽车表面正压区越大,压力偏移越明显,两侧的压力差增大,汽车气动阻力系数、侧力系数、升力系数增大,气动特性变差。
c.气动阻力系数与升力系数的优化基本协同,呈正相关;气动阻力系数、升力系数与侧力系数的优化不协同,侧力系数的改善可能引起其他2个目标的恶化。
d.综合考虑汽车气动阻力系数、侧力系数、升力系数进行的多目标优化,最终确定了4种优化方案。

