Bifurcation control of solid angle car-following model through a time-delay feedback method

Qun JI, Hao LYU, Hang YANG, Qi WEI, Rongjun CHENG

Research Article

Bifurcation control of solid angle car-following model through a time-delay feedback method

1Faculty of Maritime and Transportation, Ningbo University, Ningbo 315211, China2Ningbo University of Finance & Economics, Ningbo 315175, China

In order to alleviate unstable factor-caused bifurcation and reduce oscillations in traffic flow, a feedback control with consideration of time delay is designed for the solid angle model (SAM). The stability and bifurcation condition of the new SAM is derived through linear analysis and bifurcation analysis, and then accurate range of stable region is obtained. In order to explore the mechanism of the influence of multiple parameter combinations on the stability of controlled systems, a definite integral stabilization method is provided to determine the stable interval of time delay and feedback gain. Numerical simulations are explored to verify the feasibility and effectiveness of the proposed model, which also demonstrate that feedback gain and delay are two key factors to alleviate traffic congestion in the SAM.

Solid angle model (SAM); Time-delay; Hopf bifurcation; Feedback control; Parameter calibration

1 Introduction

With the continuous development of urbanization, traffic accidents and congestion have increasingly become obstacles to urban development. To cope with the increasing traffic demand, improve traffic efficiency, and suppress traffic congestion, scholars have conducted research on these three types of traffic flows and have proposed many traffic flow models that can describe the characteristics of real traffic flows. These models include hydrodynamic models (Ge et al., 2014), queuing models (Geroliminis et al., 2009), gas kinetic models (Helbing and Treiber, 1998), car-following models (Sun et al., 2018), and cellular automata models (Kong et al., 2021). Among them, the car-following model is the most extensively studied in micro traffic flow. It employs a dynamic approach to investigating the appropriate behavior of the following car resulting from changes in the motion state of the preceding vehicle. Currently, the most widely used research on car-following models is the optimal velocity (OV) model proposed by Bando et al. (1995), which uses acceleration changes to describe car-following behavior. For the practical deceleration situation, Helbing and Tilch (1998) established a generalized force model (GFM) to resolve these questions. Jiang et al. (2001) proposed a full velocity difference (FVD) model to further improve the acceleration and deceleration of the vehicle by considering the influence of both negative and positive speed differences on the acceleration of the rear vehicle. Based on the velocity difference model, Yu et al. (2013) proposed the full velocity difference and acceleration model (FVDAM) by considering the distance from the preceding vehicle, and the differences in velocity and acceleration from it. Cheng et al. (2017) established a newly continuous macroscopic model on the basis of FVDM, which successfully solved problems of small perturbations that previous models ignored.

With the continuous development and wide application of psychological research, scholars have gradually tried to put aside the vehicle factor and to use the human factor to describe car-following behavior by proposing a psycho-physiological model, which is based on the perception and response characteristics of the driver. This idea was first put forward by Michaels and Cozan (1963). The idea was that the driver's psycho-physiological characteristics had a certain promotion effect on the driver's safe driving, which was embodied in the driver's visual range or size of the previous car. Meanwhile, Wiedemann (1974) also discovered how psycho-physiological characteristics affect car-following behavior, and proposed a basic model of car-following, which became a core model for the well-known microscopic simulation software Vissim. The ideas of Michaels and Cozan (1963) and Wiedemann (1974) had important implications for the study of the influence of driver's psycho-physiological characteristics on driving behavior, but they also slowed down the speed of research on this topic because they were not represented by more specific models and factors. van Winsum (1999)'s research results made up for this deficiency. He developed a basic car-following model when integrating the research results of many psychologists on car-following behavior. Andersen and Sauer (2007) further improved the basic model and proposed the driving by visual angle (DVA) model. In addition, based on the full velocity difference (FVD) model of Jiang et al. (2001), Jin et al. (2011) improved the physiological car-following model, and proposed the visual angle model (VAM). Considering the characteristics of the driver's perspective, scholars believe that driver's perspective will influence safe driving during the processes of car-following and lane-changing. For this reason, Zhang et al. (2023) proposed a bi-directional visual angle model (BDVAM) that considered the collision sensitivity coefficient, rearview perspective ratio, and multiple vehicles. Furthermore, Jiang et al. (2021) considered the actual scene of a two-way road without isolation belt, and believed that the change of vehicle types in adjacent lanes would affect the driver's decision-making in car-following. Therefore, an extended VAM based on the FVD model was established to verify this feature and the results of the analysis proved it. Considering that the vehicle height will also affect the driver's perspective to a certain extent, Ma et al. (2020) proposed adding a stereo perspective to the original basic car-following model. The specific model's expression and perspective view (Fig. 1) are as follows:

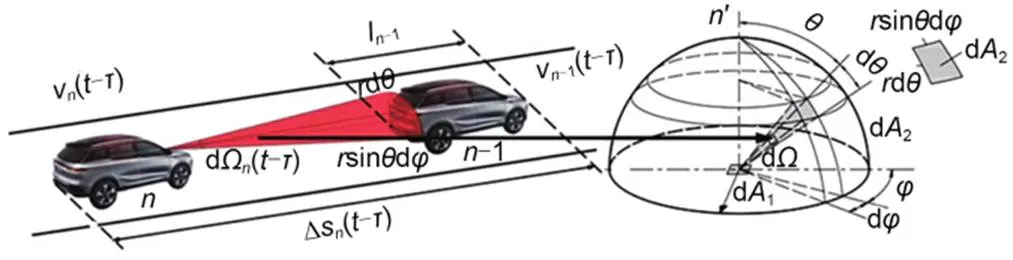
Fig. 1 Schematic diagram of solid angle

In the car-following model, the follower is affected by many factors. The main ones are the actual road design, the mechanical performance of the vehicle, and the individual characteristics of the driver (including psychological quality, driving experience, and driving age). The driver's individual characteristics are mainly reflected in the response time lag in the model. For the study of time delay, Herman et al. (1959) assumed that the driver's response came from the stimulus of the relative speed change signal, and considered the fact that there is a certain delay in the driver's response to the stimulus. They established the first time-delay car-following model. Bando et al. (1998) introduced the reaction time delay into the optimal speed model and proposed a time-delay optimization speed model. The results showed that the stability of the fleet depends not only on the size of the driver's reaction time delay, but also on the number of vehicles in the fleet. To this end, Treiber et al. (2006) incorporated the driver's response time delay into the intelligent driving model and pointed out that the negative impact of the driver's reaction time lag can be compensated by considering the behavior of multiple vehicles ahead. To further explore the influence of time delay on the system, the time delay parameters that are most conducive to the stability of the system are studied. Konishi et al. (1999) added a time-delay feedback control term based on the OV to improve traffic flow stability while suppressing traffic congestion. Das and Maurya (2022) proposed a neural network car-following model with instantaneous response delay, and the results showed that its trajectory reproduction accuracy was better than the classical model.

In addition, the time-delay control strategy was first proposed by Konishi et al. (1998), and from their conclusions we can find that time delays are important to traffic flow. On the one hand, delay can degrade control performance and even lead to system instability. On the other hand, a well-designed time-delay control system can improve the stability of traffic flow (Konishi et al., 1998). For example, Konishi et al. (2000) added a time-delay feedback control term on the basis of optimizing the speed model to improve the stability of uniform traffic flow and achieved the purpose of restraining traffic congestion. Zhao and Gao (2006) designed a new feedback controller with hysteresis based on the coupled map-following model, which effectively suppressed traffic congestion in the bottleneck section. Fang et al. (2015) designed static and dynamic feedback controllers for suppressing traffic congestion after considering the effect of continuous vehicle speed difference on traffic flow stability. In addition, bifurcation research (Jin and Xu, 2016; Zhang et al., 2019) is also highly regarded as a theoretical research method for feedback control. Ngoduy et al. (2021) established a general bifurcation structure for a car-following model with multiple time delays, and found that multiple time delays offset each other's impact on traffic instability. Guan et al. (2022) proposed a car-following model based on VAM that considers the driver's perspective and expected time.

This study establishes a controlled solid angle model (SAM) with feedback gain and response time delay, and obtains stable intervals through linear analysis and bifurcation analysis. The control effect of the feedback delay control strategy under multiple parameter combinations is simulated. Finally, the parameters of the controlled SAM are calibrated and the effectiveness of the control system is verified through simulation.

2 Controlled solid angle model

When faced with unstable situations such as traffic congestion, SAM has certain limitations. The main objective of this research is to reduce those limitations.

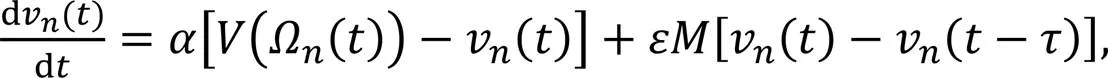
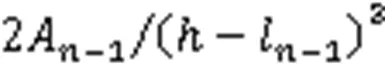
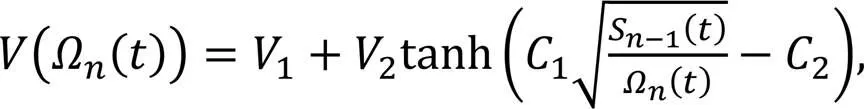
whereS-1() represents the headway of the front vehicle at timewithout considering the delay time.

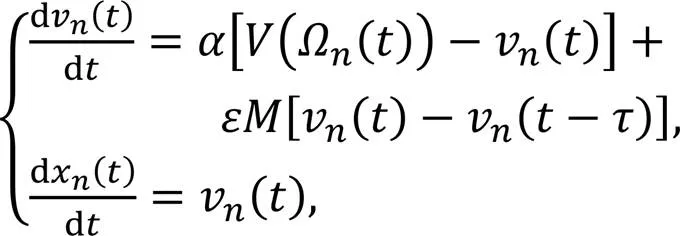
3 Linear analysis of the controlled SAM

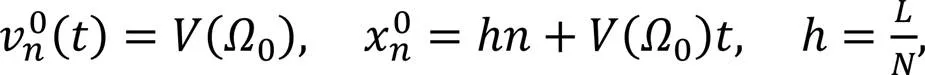
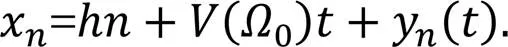
Linearizing the equation as follows:

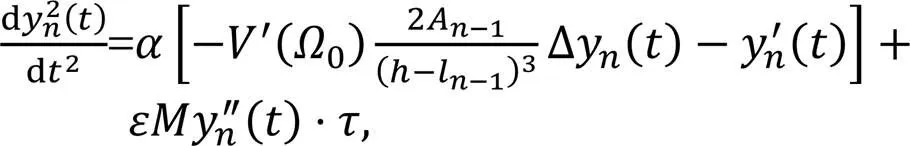
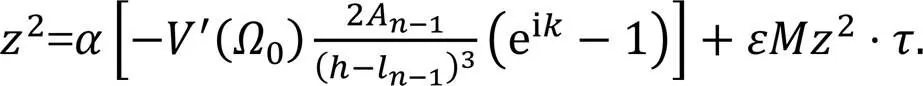
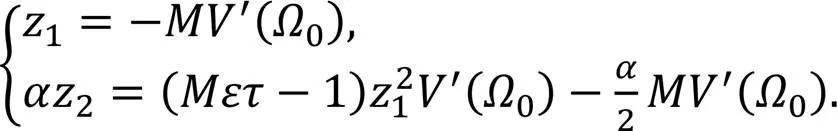
Substituting into we can obtain the expression of the neutral stability curve of the time-delay feedback control model as follows:

4 Bifurcation analysis of the controlled SAM

In this section, a bifurcation analysis is performed on a single-delay feedback-controlled SAM to study its bifurcation properties. Suppose vehicles are traveling on an adequate long single-lane circular road without overtaking. A small derivation is added for uniform flow:

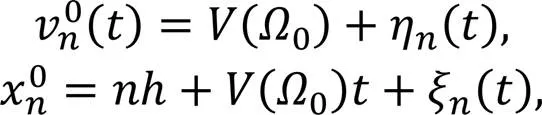
Substituting Eq. (11) into Eq. (4), we can obtain:

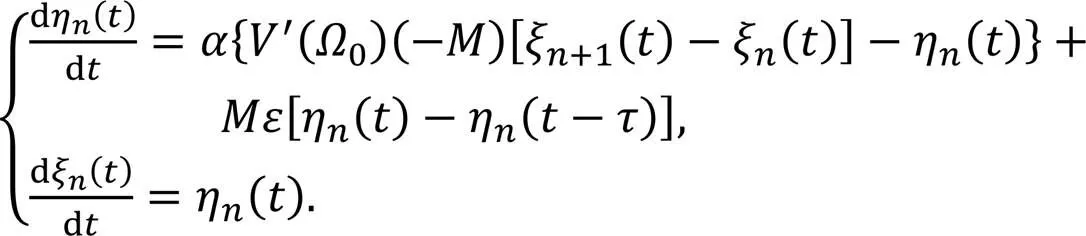
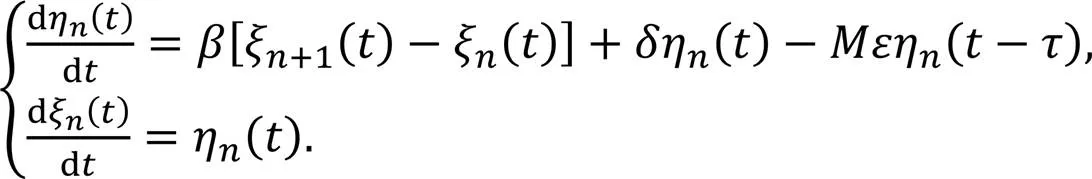
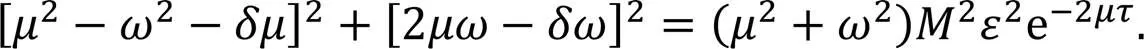
Fig. ‍3 ‍Absolute value distribution curve of SAM and controlled SAM (=1 and=7): (a) uncontrolled SAM,=0; (b) controlled SAM,=0.65 s-1, and=0.35 s

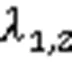
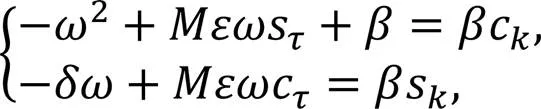
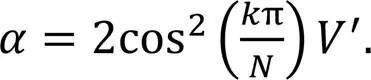
5 Design of time-delay feedback control

This section focuses on obtaining the optimal set of feedback control parameters. Among them, Jin and Xu (2016) put forward the following control principles:

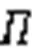
According to the control method in Section S2, the effects of multi-parameter combination for controlled system stability are explored. Some parameters are shown below:

To demonstrate the feasibility of the reaction-delay feedback control strategy, the unstable state of the SAM is compared. In Fig. 4, and the first delay interval for the controlled SAM will be predicated by plotting for different , , and . The estimate of will be obtained by the point at which the jump of occurs. The first stable reaction time interval corresponding to =0 is easily found from Fig. 4. In Figs. 4a and 4b, the feedback gains are chosen as and s-1, and the results show that the first stabilization delay regions of Figs. 4a and 4b are found to be respectively [] and []. In addition, there are second and third stable intervals [, ] and [] in Fig. 4a. By comparison, the stabilization delay interval of negative feedback (i.e. =-‍ s-1) is found to be significantly smaller than that of positive feedback (i.e. = s-1). When = s-1, and ==, the performance of positive feedback is superior to negative feedback. From Figs. 4c and 4d, the first stabilization delay interval is shown as [ ] and [ ] for fixed = s-1 and - s-1, respectively. That is, for a fixed = s-1, the controlled SAM is stable, and when the system is unstable, the traffic congestion can be alleviated by selecting the response delay in interval [ ].

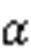
Fig. ‍5 ‍Time-varying curve of the velocity () of the first vehicle under different(where=2): (a)=0.5 s-1; (b)=-0.5 s-1

6 Case studies

6.1 Parameter calibration

This section uses 558 datasets of the 59th vehicle in the next generation simulation (NGSIM) database to calibrate the optimal parameters, which include the required data such as speed, acceleration, and distance. Because the modified dataset involves non-following vehicle trajectory data and there is changing lane behavior, the following is used as the filtering condition to satisfy the following behavior condition:

(1) The chosen vehicles should be in the same lane, and this study chooses data located in lane 1.

(2) Preceding and following vehicles are not 0.

(3) The distance between the vehicles in front and rear cannot be too large so as to ensure that vehicles are always following. Thus, this study selects 160 feet as equal to 48.768 m, which means that the Space_Headway in the dataset is no larger than 160.

After filtering through the above conditions, 558 datasets of single-lane car-following data can be acquired. The segment data of the 59th vehicle is shown in Table 1.

The least squares method is used to optimize the calibration parameters non-linearly. This method is a parametric calibration of parameters based on the minimum error between model simulation data and similar observation data. In addition, parameter combinations optimized by genetic algorithms with an error range of 5% or less were selected for analysis in both models. The normalization process is then performed for each parameter, and the results of the optimization process for each parameter are clustered systematically.

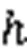
6.2 Numerical simulation

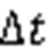
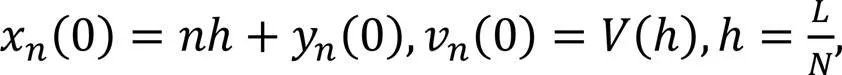
Table 1 Fragment data of the 59th vehicle following

Table 2 Calibration parameters

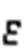
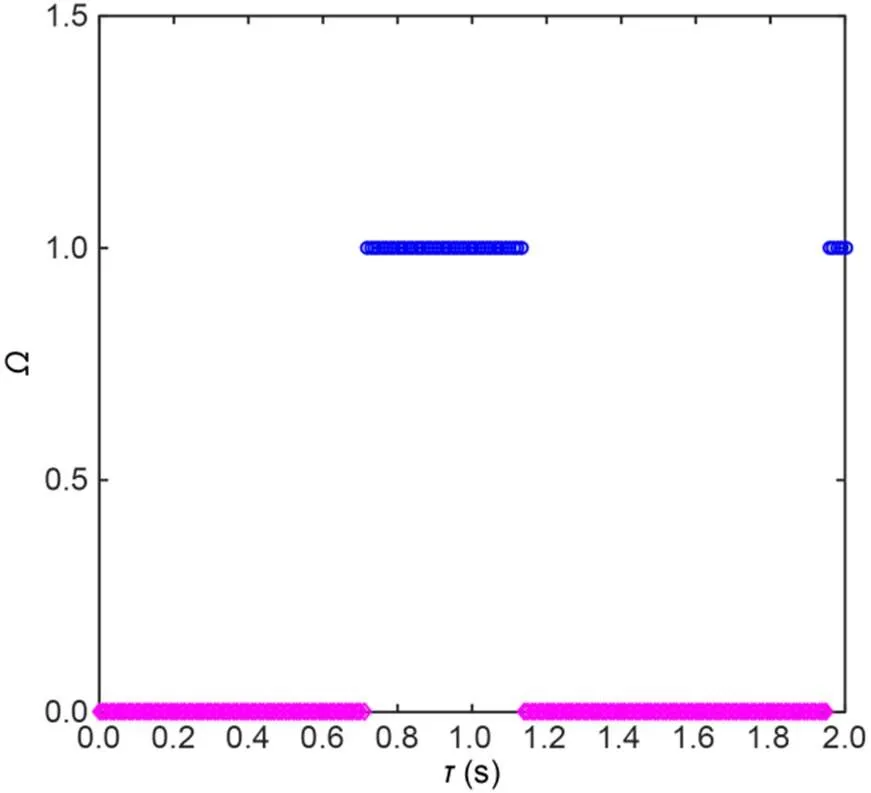
Fig. 6 Unstable root number Ω(τ) of controlled SAM (ε=0.3 s-1 and α=2.0 s-1)

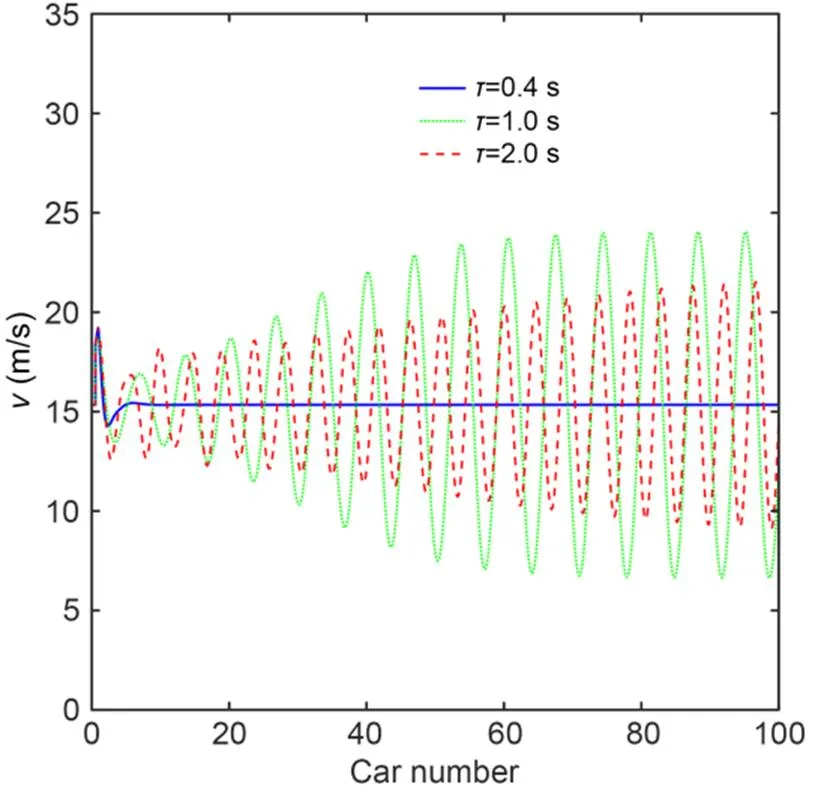
Fig. 7 Variation curve of velocity and number of vehicles under different τ (ε=0.3 s-1 and α=1.0 s-1)

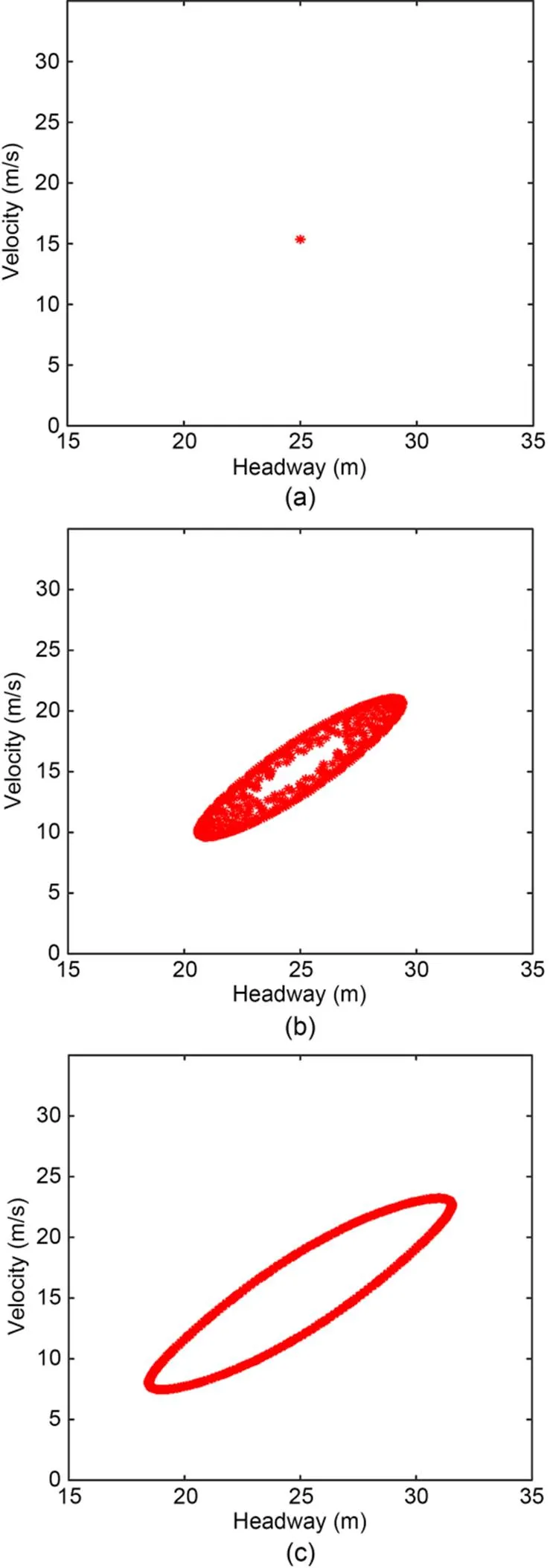
Fig. 8 Hysteresis loop of controlled SAM under different τ: (a) ε=0.3 s-1, τ=0.4 s; (b) ε=0.3 s-1, τ=1.0 s; (c) ε=0.3 s-1, τ=2.0 s

To better demonstrate the control impact of the parameter set=0.3 s-1and=0.4 s, Fig. 9 shows the density waveforms of controlled and uncontrolled SAMs, and Fig. 10 shows its 2D graph. Obviously, the irregular walking wave in Fig. 9b disappears under the control of parameter settings, which is a further proof of the effectiveness of the prediction and proposed control strategy.

7 Conclusions

In this study, a feedback control considering time delay is devised for SAM to prevent unstable factor-caused bifurcation, which will reduce oscillations in traffic flow. Precise range of stable zone is derived by contrasting the results of the linear analysis and bifurcation analysis. As the foundation for time-delay feedback control design, we provide a definite integral method, which will exploring the mechanism of the influence of multiple parameter combinations on the stability of controlled systems. More cars were employed to confirm the system's viability, and numerical simulations demonstrate that using suitable feedback gain and delay settings can really significantly increase the stability of traffic flow. Additionally highlighting the accuracy of the result, the ideal feedback gain and time delay parameters acquired by calibration are in the control system's stable zone.

However, more in-depth studies are worth conducting in the future because:

(1) This paper only applies the delayed feedback control strategy to control VAM and SAM. The control strategy can be applied to other models, such as intelligent driver model (IDM) (Xie et al. 2019) and cooperative adaptive cruise control model (Milanés and Shladover, 2014), which plays an important role in promoting the development of traffic flow theory.

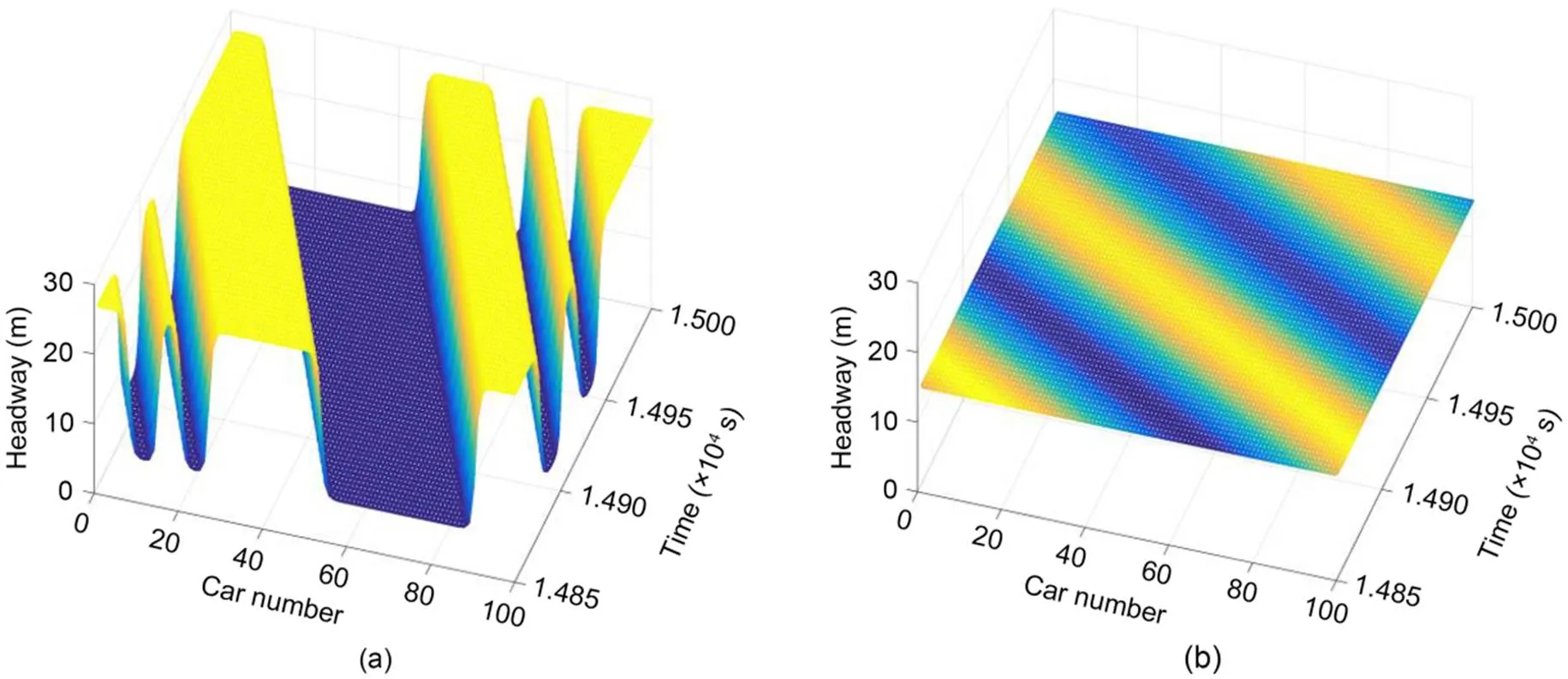
Fig. 9 Comparison between the uncontrolled SAM (ε=0) (a) and the controlled SAM (ε=0.3 s-1 and τ=0.4 s) (b)

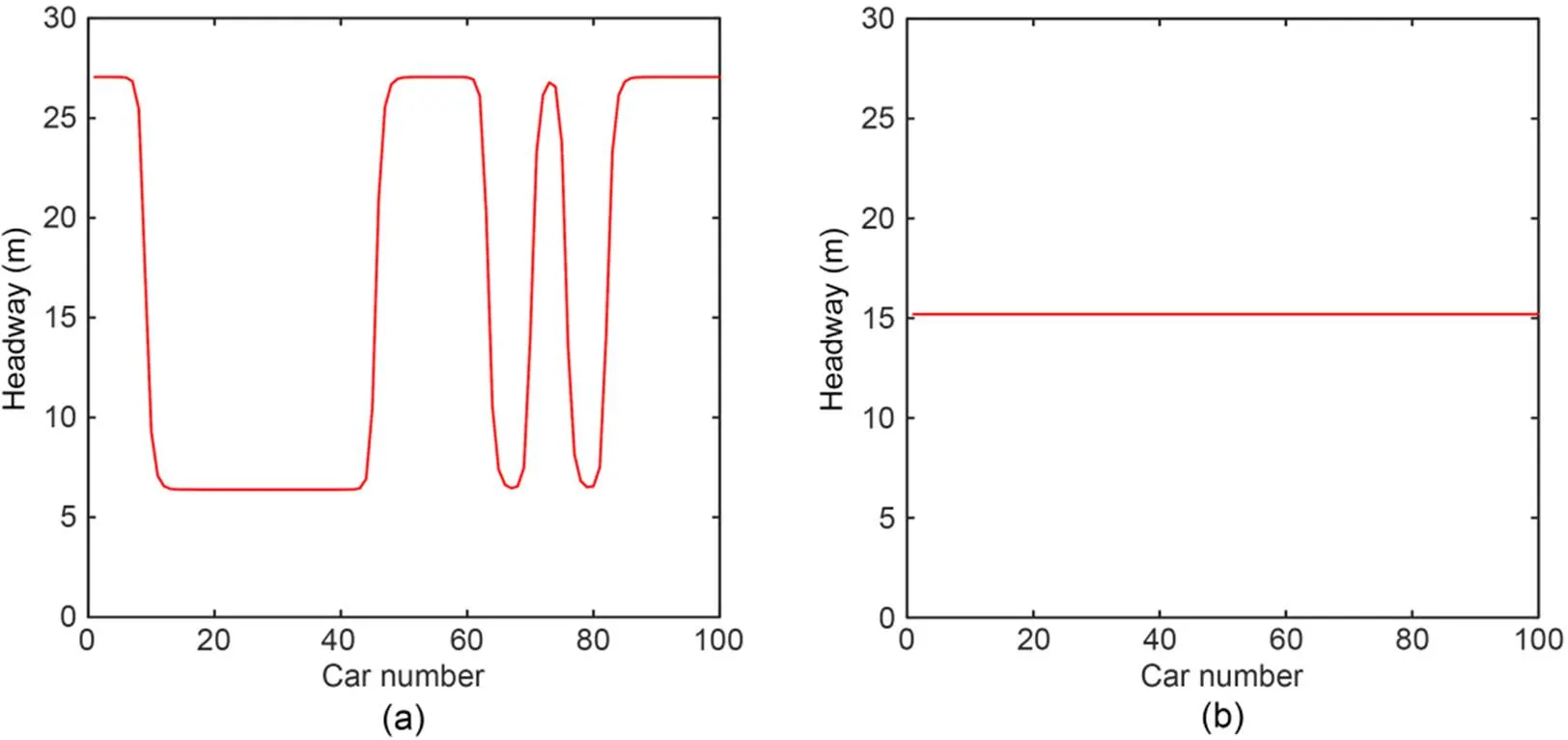
Fig. 10 Snapshots of headway for all vehicles at t=1.5×104 s corresponding to Fig. 9: (a) ε=0; (b) ε=0.3 s-1 and τ=0.4 s

(2) In the actual traffic environment, in addition to having a certain delay in responding to driving factors, drivers will also make certain predictions on driving factors based on their experience in driving scenarios. Feedback control with multiple delays and expected time helps to better control the bifurcation phenomenon of the traffic flow.

Acknowledgments

This work is supported by the National Key Research and Development Program of China (No. 2017YFE9134700), the Natural Science Foundation of Zhejiang Province, China (No. LY22G010001), the Program of Humanities and Social Science of Education Ministry of China (No. 20YJA630008), the Ningbo Natural Science Foundation of China (Nos. 2021J235 and 2021J111), the Fund of Healthy & Intelligent Kitchen Engineering Research Center of Zhejiang Province, and the K.C. Wong Magna Fund in Ningbo University, China.

Author contributions

Rongjun CHENG designed the research. Hao LYU and Hang YANG processed the corresponding data. Qun JI wrote the first draft of the manuscript. Hao LYU helped to organize the manuscript. Hang YANG revised and edited the final version. Qi WEI is responsible for numerical simulation and language polishing.

Conflict of interest

Qun JI, Hao LYU, Hang YANG, Qi WEI, and Rongjun CHENG declare that they have no conflict of interest.

Andersen GJ, Sauer CW, 2007. Optical information for car following: the driving by Visual Angle (DVA) model., 49(5):878-896. https://doi.org/10.1518/001872007X230235

Bando M, Hasebe K, Nakayama A, et al., 1995. Dynamical model of traffic congestion and numerical simulation., 51(2):1035-1042. https://doi.org/10.1103/PhysRevE.51.1035

Bando M, Hasebe K, Nakanishi K, et al., 1998. Analysis of optimal velocity model with explicit delay., 58(5):5429-5435. https://doi.org/10.1103/PhysRevE.58.5429

Cheng RJ, Liu FX, Ge HX, 2017. A new continuum model based on full velocity difference model considering traffic jerk effect., 89(1):639-649. https://doi.org/10.1007/s11071-017-3477-2

Das S, Maurya AK, 2022. A car-following model considering driver’s instantaneous reaction delay in nonlane-based traffic environments., 148(8):1-13.https://doi.org/10.1061/JTEPBS.0000709

Fang YL, Shi ZK, Cao JL, 2015. Congestion phenomenon analysis and delayed-feedback control in a modified coupled map traffic flow model containing the velocity difference., 23(1-3):175-184. https://doi.org/10.1016/j.cnsns.2014.11.007

Ge HX, Zheng PJ, Lo SM, et al., 2014. TDGL equation in lattice hydrodynamic model considering driver’s physical delay., 76(1):441-445. https://doi.org/10.1007/s11071-013-1137-8

Geroliminis N, Karlaftis MG, Skabardonis A, 2009. A spatial queuing model for the emergency vehicle districting and location problem., 43(7):798-811. https://doi.org/10.1016/j.trb.2009.01.006

Guan XY, Cheng RJ, Ge HX, 2022. Bifurcation analysis of visual angle model with anticipated time and stabilizing driving behavior., 31:070507. https://doi.org/10.1088/1674-1056/ac5606

Helbing D, Treiber M, 1998. Gas-kinetic-based traffic model explaining observed hysteretic phase transition., 81(14):3042-3045. https://doi.org/10.1103/PhysRevLett.81.3042

Helbing D, Tilch B, 1998. Generalized force model of traffic dynamics., 58(1):133-138. https://doi.org/10.1103/PhysRevE.58.133

Herman R, Montroll EW, Potts RB, et al., 1959. Traffic dynamics: analysis of stability in car following., 7(1):86-106. https://doi.org/10.1287/opre.7.1.86

Jiang N, Yu B, Cao F, et al., 2021. An extended visual angle car-following model considering the vehicle types in the adjacent lane., 566:125665. https://doi.org/10.1016/j.physa.2020.125665

Jiang R, Wu QS, Zhu ZJ, 2001. Full velocity difference model for a car-following theory., 64(1):017101. https://doi.org/10.1103/PhysRevE.64.017101

Jin S, Wang DH, Huang ZY, et al., 2011. Visual angle model for car-following theory., 390(11):1931-1940. https://doi.org/10.1016/j.physa.2011.01.012

Jin YF, Xu M, 2016. Stability analysis in a car-following model with reaction-time delay and delayed feedback control., 459:107-116. https://doi.org/10.1016/j.physa.2016.04.038

Kong DW, Sun LS, Li J, et al., 2021. Modeling cars and trucks in the heterogeneous traffic based on car-truck combination effect using cellular automata., 562:125329. https://doi.org/10.1016/j.physa.2020.125329

Konishi K, Hirai M, Kokame H, 1998. Decentralized delayed-feedback control of a coupled map model for open flow., 58(3):3055-3059. https://doi.org/10.1103/PHYSREVE.58.3055

Konishi K, Kokame H, Hirata K, 1999. Coupled map car-following model and its delayed-feedback control., 60(4):4000-4007. https://doi.org/10.1103/PhysRevE.60.4000

Konishi K, Kokame H, Hirata K, 2000. Decentralized delayed-feedback control of an optimal velocity traffic model., 15(4):715-722. https://doi.org/10.1007/s100510051176

Ma DF, Han YY, Jin S, 2020. Solid angle car following model., 29(6):060504. https://doi.org/10.1088/1674-1056/ab862c

Michaels RM, Cozan LW, 1963. Perceptual and field factors causing lateral displacement., 25:1-13.

Milanés V, Shladover SE, 2014. Modeling cooperative and autonomous adaptive cruise control dynamic responses using experimental data., 48:285-300. https://doi.org/10.1016/j.trc.2014.09.001

Ngoduy D, Li TL, 2021. Hopf bifurcation structure of a generic car-following model with multiple time delays., 17(4):878-896. https://doi.org/10.1080/23249935.2020.1818002

Ossen S, Hoogendoorn SP, Gorte BGH, 2006. Interdriver differences in car-following: a vehicle trajectory-based study., 1965(1):121-129. https://doi.org/10.1177/0361198106196500113

Sun J, Zheng ZD, Sun J, 2018. Stability analysis methods and their applicability to car-following models in conventional and connected environments., 109:212-237. https://doi.org/10.1016/j.trb.2018.01.013

Treiber M, Kesting A, Helbing D, 2006. Delays, inaccuracies and anticipation in microscopic traffic models., 360(1):71-88. https://doi.org/10.1016/j.physa.2005.05.001

van Winsum W, 1999. The human element in car following models., 2(4):207-211. https://doi.org/10.1016/S1369-8478(00)00008-5

Wiedemann R, 1974. Simulation of Road Traffic in Traffic Flow. University of Karlsruhe, Karlsruhe, Germany.

Xie DF, Zhao XM, He ZB, 2019. Heterogeneous traffic mixing regular and connected vehicles: modeling and stabilization., 20(6):2060-2071. https://doi.org/10.1109/TITS.2018.2857465

Yu SW, Liu QL, Li XH, 2013. Full velocity difference and acceleration model for a car-following theory., 18(5):1229-1234. https://doi.org/10.1016/j.cnsns.2012.09.014

Zhang XZ, Shi ZK, Chen JZ, et al., 2023. A bi-directional visual angle car-following model considering collision sensitivity., 609:128326. https://doi.org/10.1016/j.physa.2022.128326

Zhang YC, Xue Y, Zhang P, et al., 2019. Bifurcation analysis of traffic flow through an improved car-following model considering the time-delayed velocity difference., 514:133-140. https://doi.org/10.1016/j.physa.2018.09.012

Zhao XM, Gao ZY, 2006. A control method for congested traffic induced by bottlenecks in the coupled map car-following model., 366:513-522. https://doi.org/10.1016/j.physa.2005.11.004

Sections S1‍ and S2, Eqs. (S1)‒(S13)

https://doi.org/10.1631/jzus.A2300026

Revision accepted Mar. 2, 2023;

Crosschecked July 28, 2023

© Zhejiang University Press 2023

Jan. 12, 2023;