Finite-time path following control of a sailboat with actuator failure and unknown sideslip angle

Yujin WU, Kangjian SHAO, Ning WANG, Zhongchao DENG

Research Article

Finite-time path following control of a sailboat with actuator failure and unknown sideslip angle

1Science and Technology on Underwater Vehicle Laboratory, Harbin Engineering University, Harbin 150001, China2School of Marine Engineering, Dalian Maritime University, Dalian 116026, China

Suffering from actuator failure and complex sideslip angle, the motion control of a sailboat becomes challenging. In this paper, an improved double finite-time observer-based line-of-sight guidance and finite-time control (IDFLOS-FC) scheme is presented for path following of sailboats. The salient features of the proposed IDFLOS-FC scheme are as follows: (1) Considering the problem of actuator failure, an actuator failure model is introduced into the dynamics model of a sailboat. (2) The time-varying sideslip angle of the sailboat is accurately observed by the double finite-time sideslip observers (DFSOs), which reduces the error in line-of-sight (LOS) guidance. (3) A radial basis function (RBF) neural network is used to fit the uncertainty of the model, and the upper bound of the sum of fault effects and external disturbances is estimated based on adaptive theory, so that the controller has accurate tracking and interference suppression. (4) According to the Lyapunov method, the system is finite-time stable. Finally, simulation was used to validate the effectiveness of the method.

Sailboat; Sideslip angle; Sideslip angle observer; Finite-time control (FC); Path following

1 Introduction

Over recent decades, unmanned surface vehicles (USVs) have contributed greatly to marine military and commercial fields with their outstanding independent capabilities and excellent comprehensive performance (Manley, 2008; Liu et al., 2016; Wang et al., 2022). However, due to limitations, a traditional USV is not suitable for performing prolonged and complex tasks. An unmanned sailboat is assisted by wind, which reduces energy consumption and has significant advantages in performing large-scale and long-term tasks (Wang et al., 2019; Hong et al., 2020). Therefore, research on unmanned sailboats for marine exploration and improving maritime safety has great potential value.

An unmanned sailboat needs to be equipped with navigation and control systems to complete its autonomous navigation tasks. At present, research is carried out mainly around the platform body, navigation system, and control system of unmanned sailboats, which are interrelated and inseparable. The platform ontology provides the basic conditions for the autonomous navigation of unmanned sailboats, and the navigation system and control system play important roles in their autonomous missions.

In navigation, the conventional line-of-sight (LOS) guidance strategy is an effective navigation algorithm that has been widely used in USVs. Pettersen and Lefeber (2001) applied LOS to way-point tracking control. Liu et al. (2017) proposed an improved LOS guidance algorithm that can adjust adaptively according to the path tracking error. Li et al. (2023) integrated LOS guidance into the formation strategy under the leader-follower scheme and achieved good results. In actual navigation, unmanned sailboats are prone to sideslip, which is irregular and difficult to measure, and this adversely affects the accuracy of LOS guidance. Xia et al. (2019) proposed an LOS guidance law with large sideslip angle compensation to obtain the command heading angle signal for the control system. Liu (2022) designed an improved extended state observer-based LOS (ELOS) for estimating complex sideslip angle. A finite-time observer-based LOS was designed by Wang et al. (2018), in which the sideslip angle was accurately observed at short notice.

In terms of control, path following technology is crucial for the implementation of various key tasks, which determines the technical level and comprehensive performance of unmanned sailboats. For the convenience of calculation, most scholars ignored the roll motion of USVs (Wille et al., 2016; Viel et al., 2018; Dos Santos and Goncalves, 2019). However, due to the existence of sails, the roll response of unmanned sailboats needs to be considered. Xiao and Jouffroy (2014) proposed a four-degree-of-freedom (DOF) mathematical model of a keel-sailboat that took roll moment into consideration, but did not consider the influence of external disturbance. To ensure the accuracy of path following, the influence of external disturbance should be considered. Cui et al. (2016) summarized the external disturbance and model uncertainty as aggregate uncertainties and observed them using an adaptive disturbance observer with good results. Ma et al. (2021) presented an event-based switched USV control system to account for the simultaneous presence of communication delays, disturbance, faults, and denial-of-service (DoS) jamming attacks. Xu et al. (2020) used a radial basis function (RBF) neural network to estimate the external disturbance of a USV. In the control domain, accurate tracking of the desired path is a prerequisite and key for USVs to accomplish various tasks. For the trajectory tracking problem of marine aerial-surface heterogeneous (MASH) system, Wang and Ahn (2021) proposed a coordinated trajectory-tracking control (CTTC) scheme and obtained better tracking results. To solve the trajectory tracking problem of an asymmetric underactuated surface vehicle, Wang and Su (2021) designed a finite-time unknown observer-based interactive trajectory tracking control (FUO-ITTC) scheme, and the experimental results showed that the scheme has a good performance in both transient and steady state tracking. Wang et al. (2021) developed a novel reinforcement learning-based optimal tracking control (RLOTC) scheme for a USV in the presence of complex unknowns, including dead-zone input nonlinearities, system dynamics, and disturbances. Simulation results showed that the scheme has significant effectiveness and superiority.

An unmanned sailboat with solar power generation equipment can perform long-term operations at sea and can complete an information collection task well under the normal operation of the system. However, long-term work has led to the failure of some equipment. The presence of sails has caused great disturbance at sea. In particular, the rudder control actuator has to be adjusted according to the external environment, which increases the wear of the actuator. Therefore, it is necessary to study the fault-tolerant control of unmanned sailboats. At present, fault control of surface ships can be solved by robust control. An actuator robust fault-tolerant control method for a USV with unknown model and disturbance was proposed by Chen et al. (2016). Considering the failure of the USV's propulsion device, the actuator fault-tolerant controller was proposed in combination with the actuator configuration matrix and the change of the actuator configuration matrix caused by the rotatable propulsion device. Wang and Deng (2020) designed a finite-time fault estimation method using a finite-time observer and solved the USV trajectory tracking problem under an unknown actuator fault, input saturation, and uncertainty, and proved that the system error is finite-time convergent. Wan et al. (2022) designed a fixed-time observer to solve the unknown actuator failure problem, and a nonlinear fast fixed-time terminal sliding mode to improve the speed of system convergence. The system error showed fixed-time convergence. Qin et al. (2020) designed fault-tolerant control laws through tan-shaped Lyapunov functions to limit errors and improve the robustness of the system after actuator failure. Emami and Banazadeh (2020) studied the problem of USV trajectory tracking under sensor failure and designed a closed-loop system with fault-tolerant capability based on model predictive control. Fu et al. (2018) designed a time-varying sliding mode controller with neural network estimation for yaw angle and yaw speed oscillation caused by thruster faults and disturbances. Zhou et al. (2019) designed a network-based fault estimation scheme, which estimates the state and fault of a USV simultaneously in the network environment, and proposed a fault-tolerant controller based on a fault observer. For sailboats, the existing fault-tolerant controllers are gradually stable. In practice, the limited time stability can make sailboats quickly recover to a normal state in the case of actuator failure.

Inspired by the above academic results, this paper combines observer and LOS guidance to enhance the guidance accuracy, and designs the control law based on finite-time theory to realize the accurate tracking of the sailboat on the desired path. The main contributions of this paper are as follows:

(1) The designed double finite-time sideslip observer (DFSO) compensates the time-varying sideslip angle in real time, thus improving the accuracy of LOS guidance.

(2) Finite-time filter is designed so as to avoid repeated derivation of the virtual control law.

(3) The fault model of the unmanned sailboat is considered, and a non-singular terminal sliding mode with adaptive parameter adjustment is designed to enhance the robustness of the system and prevent the system from leaving the equilibrium state when the actuator suddenly fails.

(4) Considering the problem of model uncertainty, the minimum parameter estimation method is used to estimate the uncertain part of the unmanned sailboat model, and a fault-tolerant control method for an unmanned sailboat based on an adaptive parameter adjustment sliding mode is designed. The error of the heading control system is proved to have finite-time convergence.

2 Problem formulations

Fig. 1 Sailboat in different coordinates. Reprinted from (Shao et al., 2023), Copyright 2023, with permission from Springer Nature

The kinematic and dynamic model of a 4-DOF unmanned sailboat can be expressed as follows (Xiao and Jouffroy, 2014):

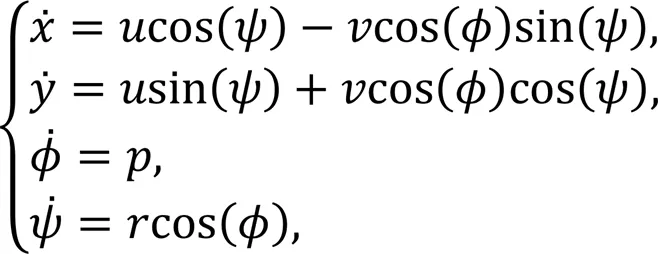
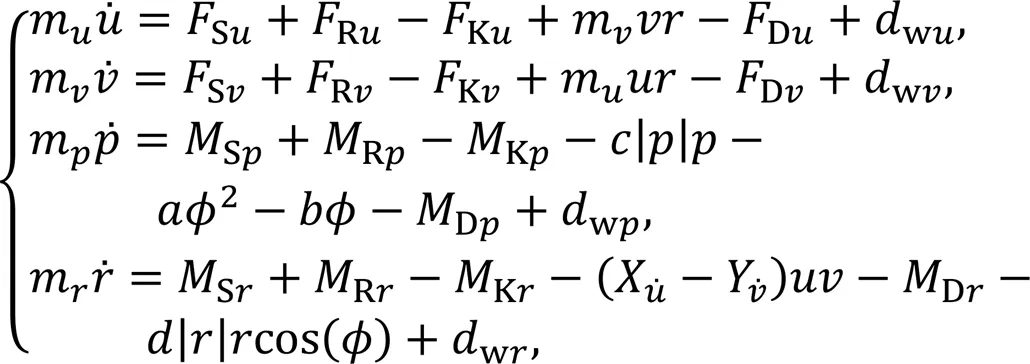
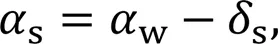
The lift and drag forces of the sailsandsare

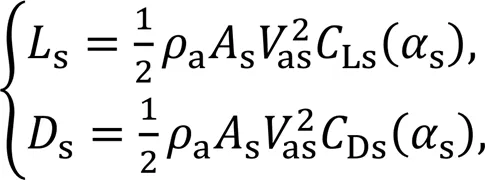
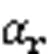
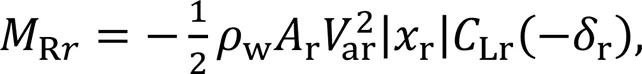
3 Sideslip angle observation and LOS guidance

In order to observe the time-varying sideslip angle to improve the LOS guidance accuracy, double finite-time sideslip angle observers are designed in this section.

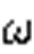
Fig. ‍2 ‍Path following control geometry of a sailboat. Reprinted from (Shao et al., 2023), Copyright 2023, with permission from Springer Nature

The time derivative of Eq. (6) is

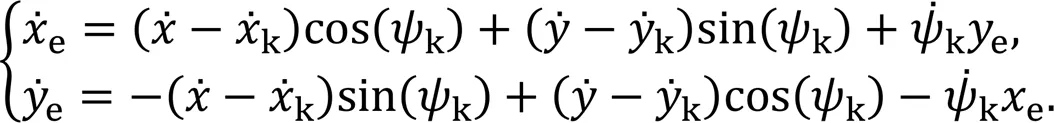
Substituting Eq. (1) into Eq. (7), we have

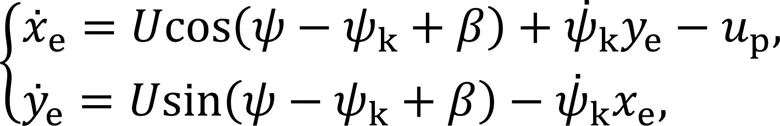
Design the double finite-time sideslip angle observers as

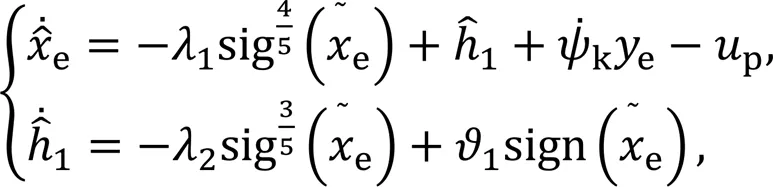
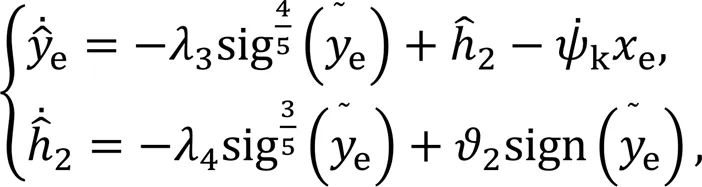
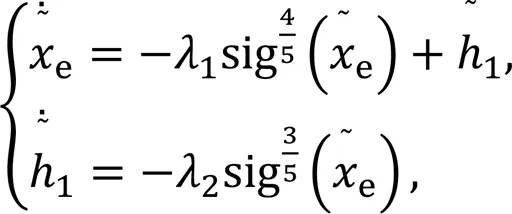
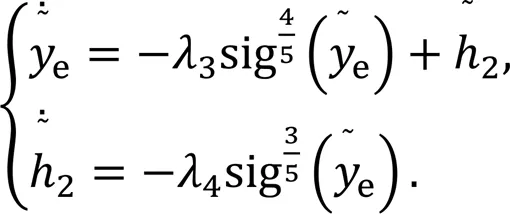
The estimated value of the sideslip angle is

Then the error of sideslip angle is expressed as

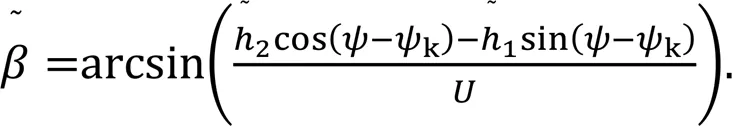
The LOS method tracking angle is expressed as

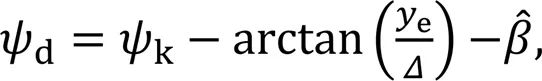
Substituting Eqs. (9) and (16) into Eq. (8), it can be obtained as

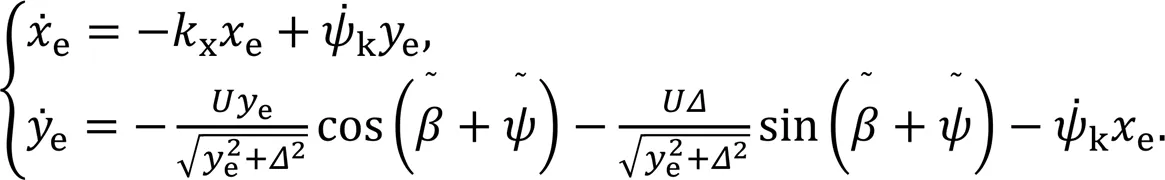
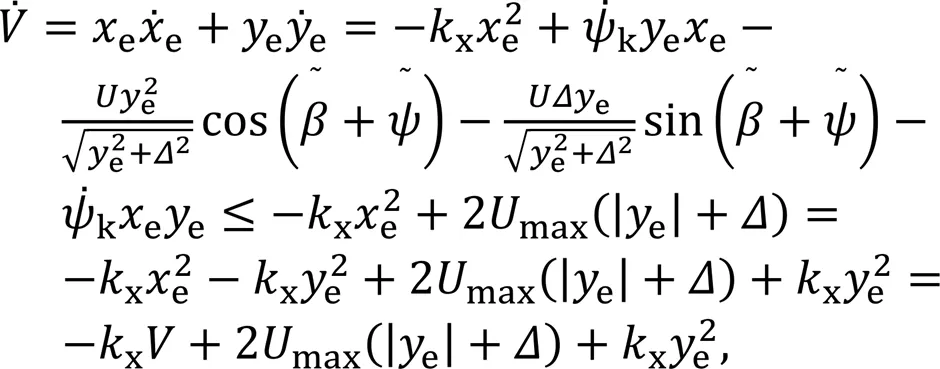
4 Heading control

4.1 Controller design

Considering heading control, Eqs. (1) and (2) can be simplified as

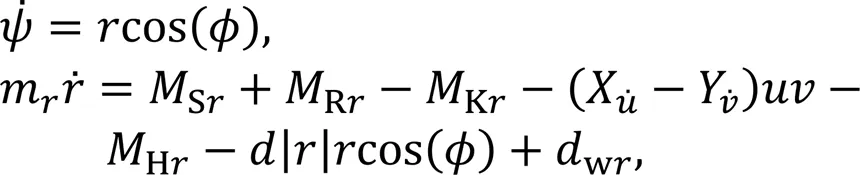
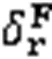
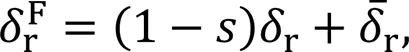
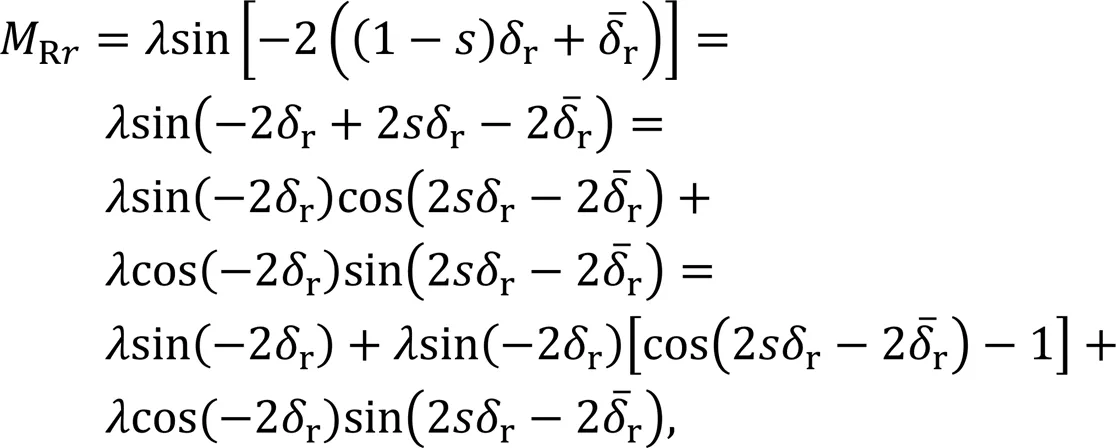
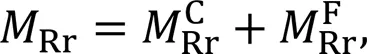
Considering the actual situation of the cruise, the following assumptions were made.

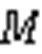
Bringing Eq. (22) into Eq. (19), the dynamics model of the heading motion of the unmanned sailboat can be written as

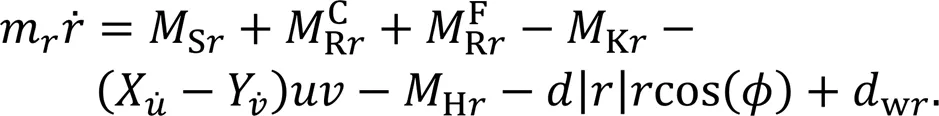
Define the heading tracking error as follows:

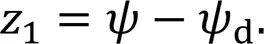
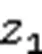
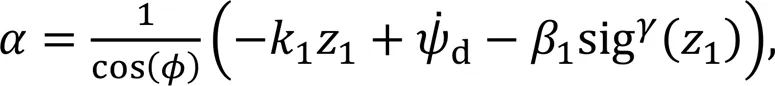
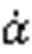
The filter output error is defined as

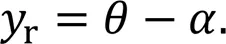
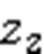
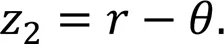
The Lyapunov candidate function is selected according to the heading tracking error as

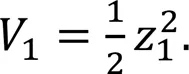
The derivative of the Lyapunov candidate function with respect to time yields

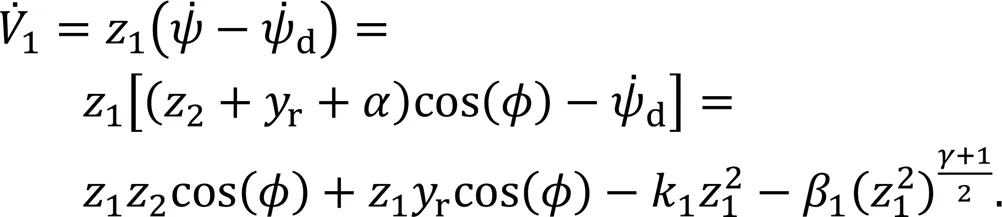
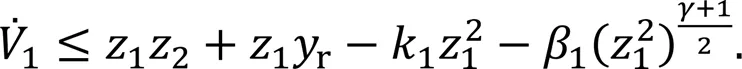
According to Young's inequality, the following inequality holds:

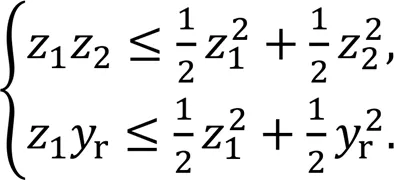
Then Eq. (31) can be expressed as

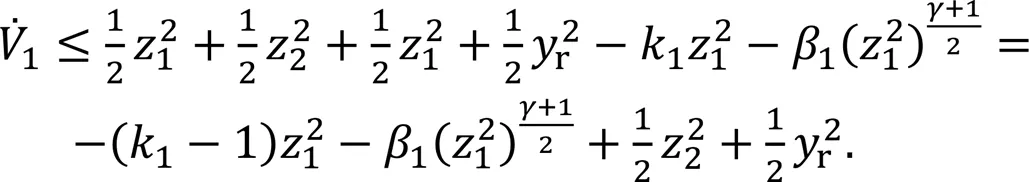
Considering the large tracking error generated after the failure of the sailboat actuator, a robust sliding mode controller with adaptive regulation parameters was designed by simplifying some of the regulation parameters and adding an integral term according to Guo et al. (2021). The adaptive regulation parameters were designed to make faster convergence to the sliding mode surface, and the fault-tolerant controller was designed using adaptive parameters.

The sliding surface was designed as

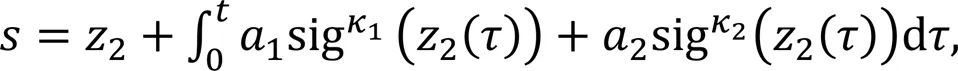
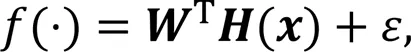
The uncertainty term is expressed as

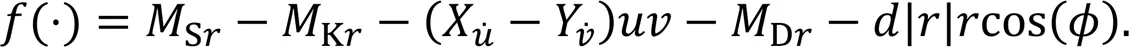
Directly using the RBF neural network to approximate the uncertainty term, the weight matrix needs to be learned online in real time, and the computation is large. To solve the problem of the large computation of the neural network, the minimum parameter method is used instead of a neural network algorithm, as follows:

Define the one-parameter adaptive law as

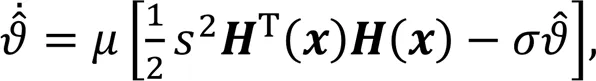
whereandare positive constants.

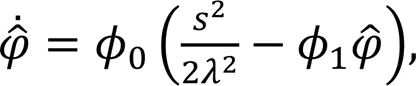
In summary, the rudder angle control law for the design of an unmanned sailboat is

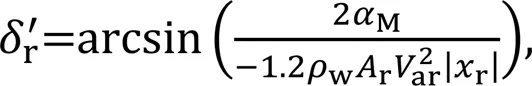
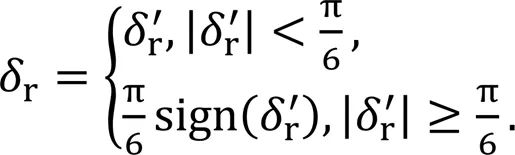
4.2 Stability analysis

Design the Lyapunov candidate function as follows:

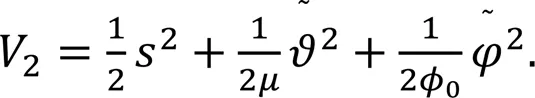
The derivative of the Lyapunov candidate function with respect to time yields

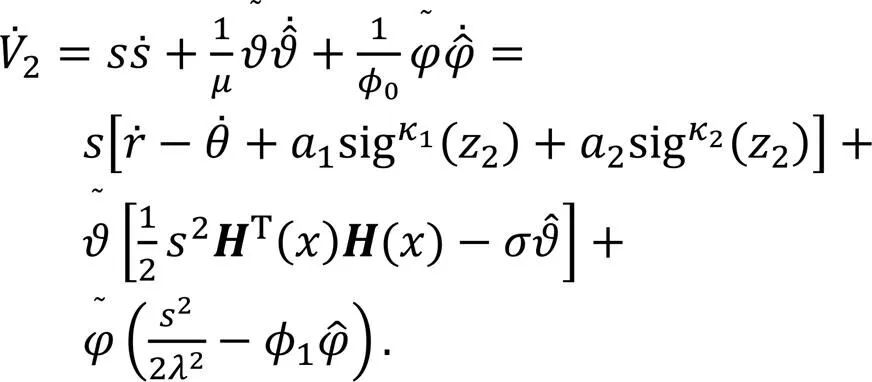
Bringing in the heading control law, the following inequality is obtained:

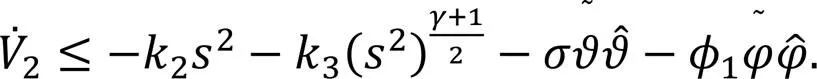
According to Young's inequality, the following equations hold:

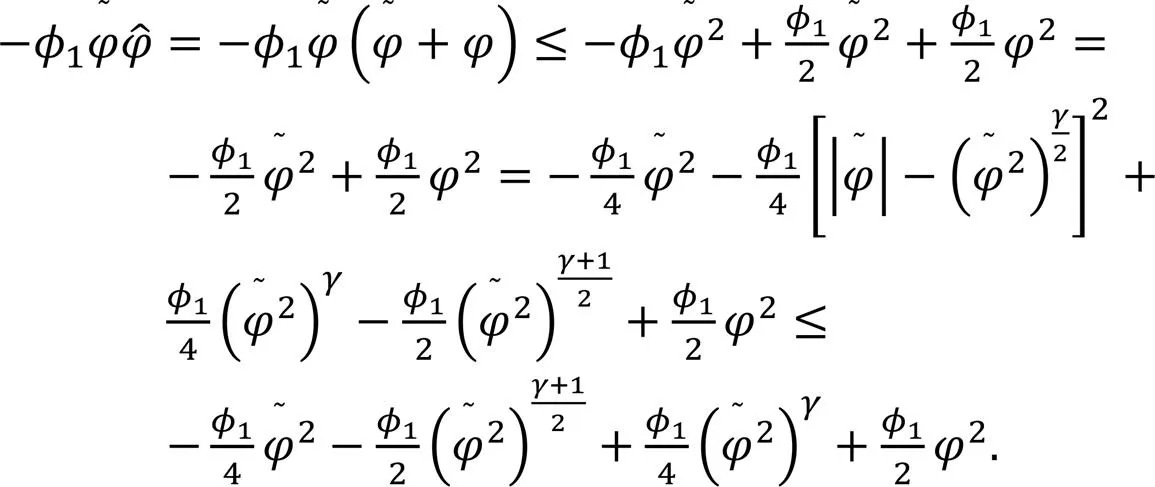
In summary, it can be obtained that

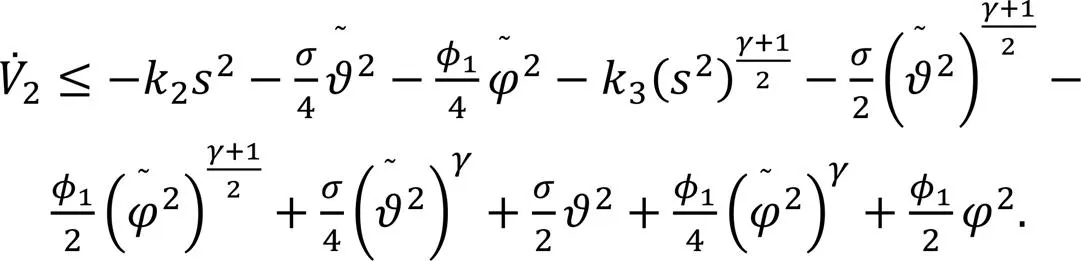
Design the Lyapunov function as

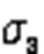
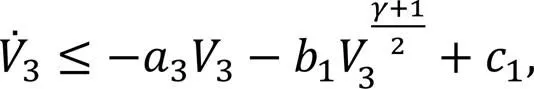
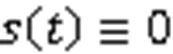
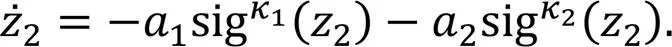
Therefore, the convergence of the system is discussed when the error is stabilized to the sliding mode surface. The Lyapunov candidate function is defined as

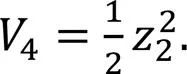
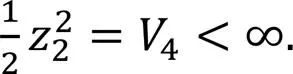
In addition, the following inequalities are given by

We have

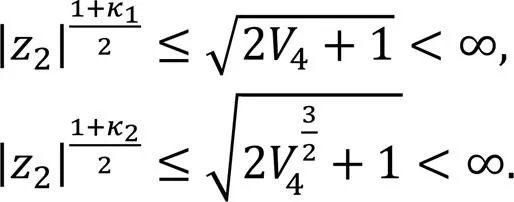
From Eq. (53), we can obtain:

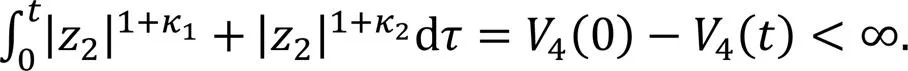
Therefore, combining Eqs. (56) and (57), from Barbalat's theorem, we have

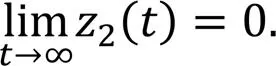
The control algorithm in this study is shown in Fig. 3. When the unmanned sailboat is subject to external interference caused by wind and waves, and the rudder actuator has a failure that will reduce its performance, the controller respectively designs the adaptive adjustment parameter sliding mode and fault-tolerant adaptive items to compensate for the actuator failure and external disturbance. This improves the robustness of the actuator in case of its failure, and achieves a more accurate path following control.

5 Simulation studies

To demonstrate the feasibility and effectiveness of the proposed improved double finite-time observer-based line-of-sight guidance and finite-time control (IDFLOS-FC) scheme, simulation study is conducted on the sailboat. To reflect more realistic working conditions, we have added wind and wave disturbance forces (Fossen, 2011). The wind speed was set to 5 m/s and the wind angle was set to 5°. The height of the meaningful wave was set to 0.7 m, and the desired path is designed as

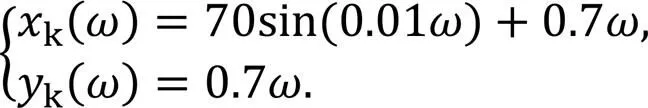
The hydrodynamic parameters were chosen as follows: m= = =, =, and =-. The initial position of the unmanned sailboat in the simulation was (-25 m, 0 m), the initial longitudinal velocity was 1 m/s, and the initial values of the remaining states were set to zero. The control parameters were set to: =, =, =, =, =, =, =, =,=, =, = , = , = , = , = , =, =, =, =, =, =, =, =, =, and =.

Next, to verify the control effect of the controller designed in this study under the condition of actuator failure, we designed two test schemes as follows:

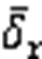
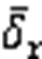
5.1 Simulation results of Scheme 1

The simulation results are shown in Figs. 4‍–‍10. The simulation effect of path following is shown in Fig. 4, which shows that the designed IDFLOS-FC scheme quickly converged to the desired path in about 20 s, and had high path following accuracy. Fig. 5 shows the control performance of the unmanned sailboat after the effect of the actuator rudder failure. Both the lateral and longitudinal errors of IDFLOS-FC are stabilized in a short time. Fig. 6 shows that the designed DFSO has good observation of the time-varying sideslip angle. Fig. 7 shows the heading tracking error converged to 0 at about 10 s. Fig. 8 shows the curve of the rudder angle over time and Fig. 9 shows the curve of the sail angle over time. Fig. 10 shows the change of roll angle with time. The maximum roll angle of the sailboat did not exceed 30°, which is in line with the actual navigation.

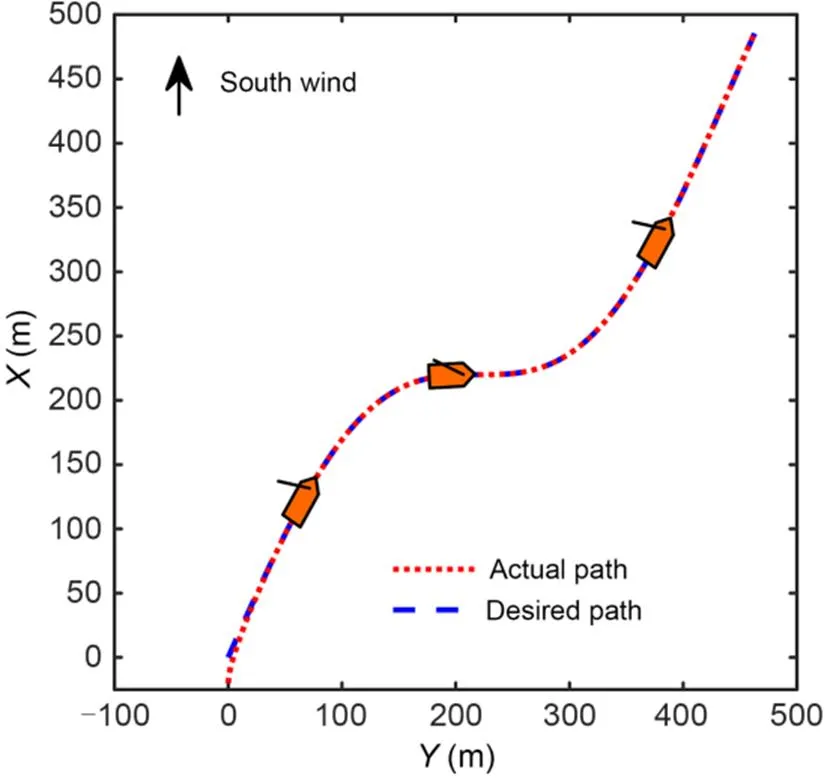
Fig. 4 Path following performance of the sailboat

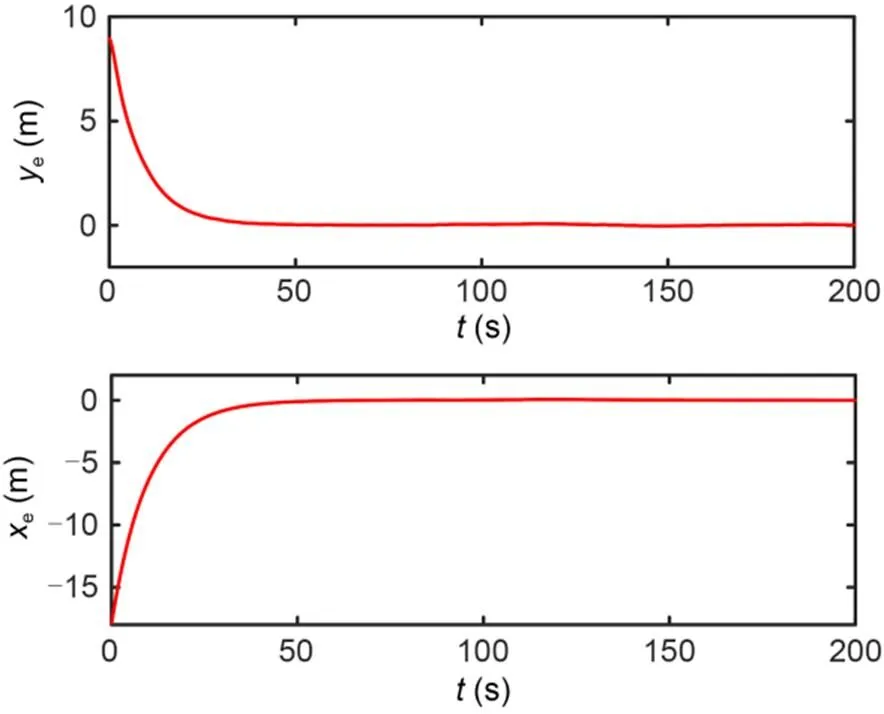
Fig. 5 Path tracking error (xe, ye)

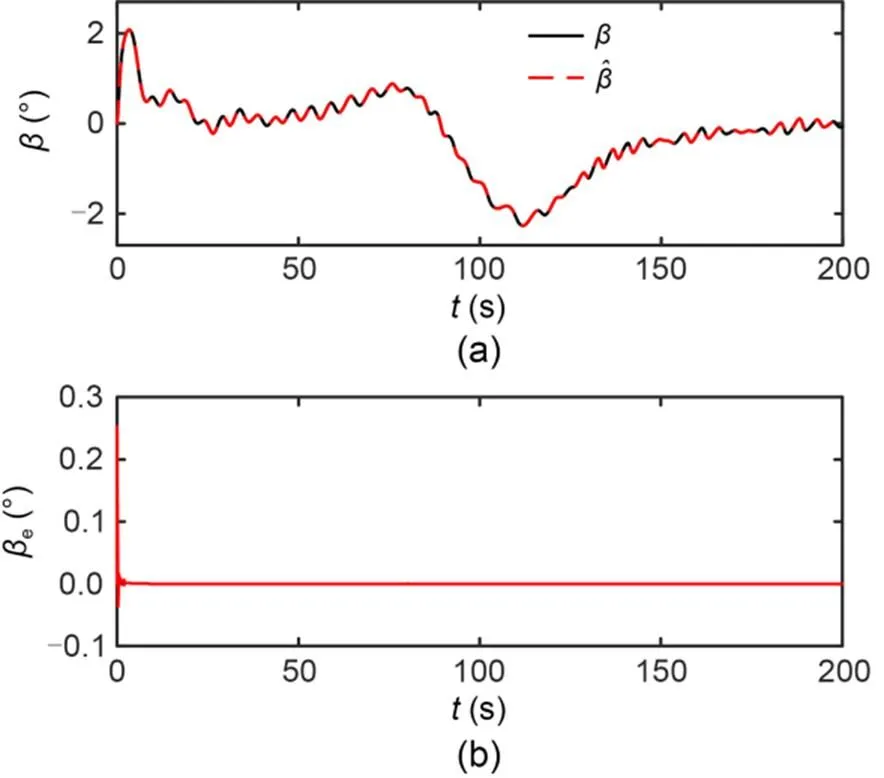
Fig. 6 Estimation (a) and error (b) of the sideslip angle

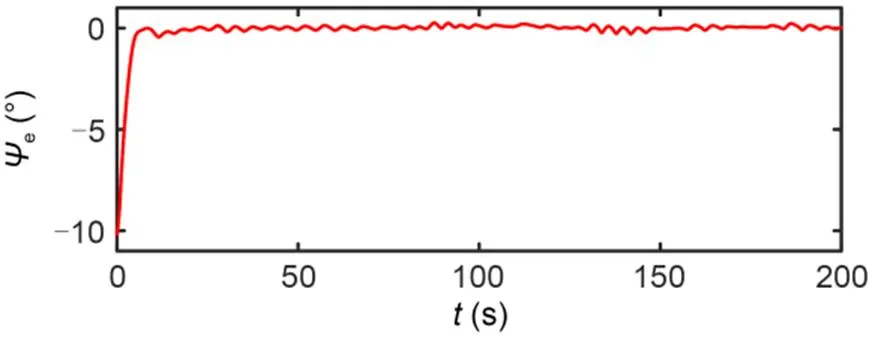
Fig. 7 Heading angle tracking error

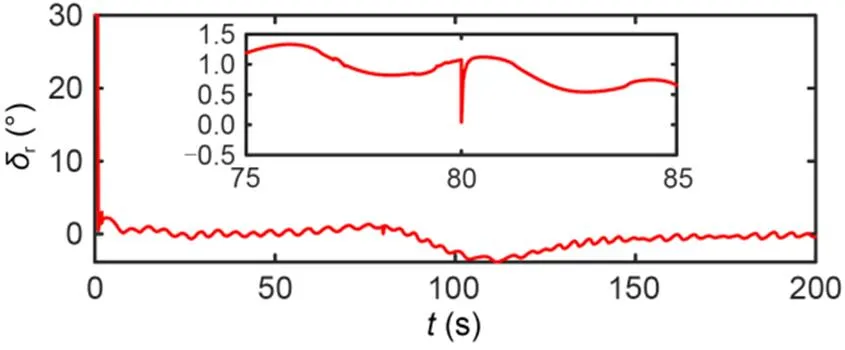
Fig. 8 Control input

Fig. 9 Control input

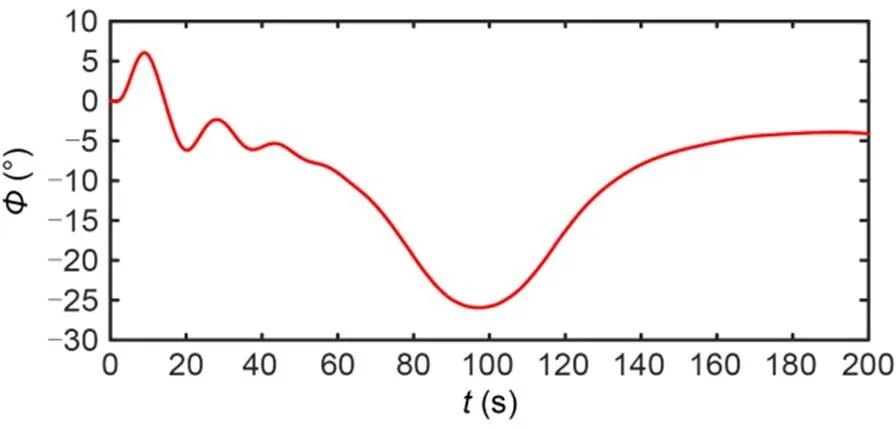
Fig. 10 Variation of sailboat roll angle

5.2 Simulation results of Scheme 2

The simulation results are shown in Figs. 11‍–‍17. Fig. 11 shows that the designed IDFLOS-FC scheme can accurately track the desired path even if a fault is added. Fig. 12 shows that the lateral and longitudinal errors of the designed IDFLOS-FC scheme converged to zero in about 50 s. Fig. 13 shows that the designed DFSO accurately observed the sideslip angle even when the fault was increased. The heading tracking error converged to 0 in about 10 s (Fig. 14). After increasing the fault, the heading tracking deviated, but still maintained good tracking ability under the control law. Fig. 15 and Fig. 16 show the curves of the rudder angle and sail angle over time, respectively. Fig. 17 shows the change of roll angle with time, which was in line with the actual navigation.

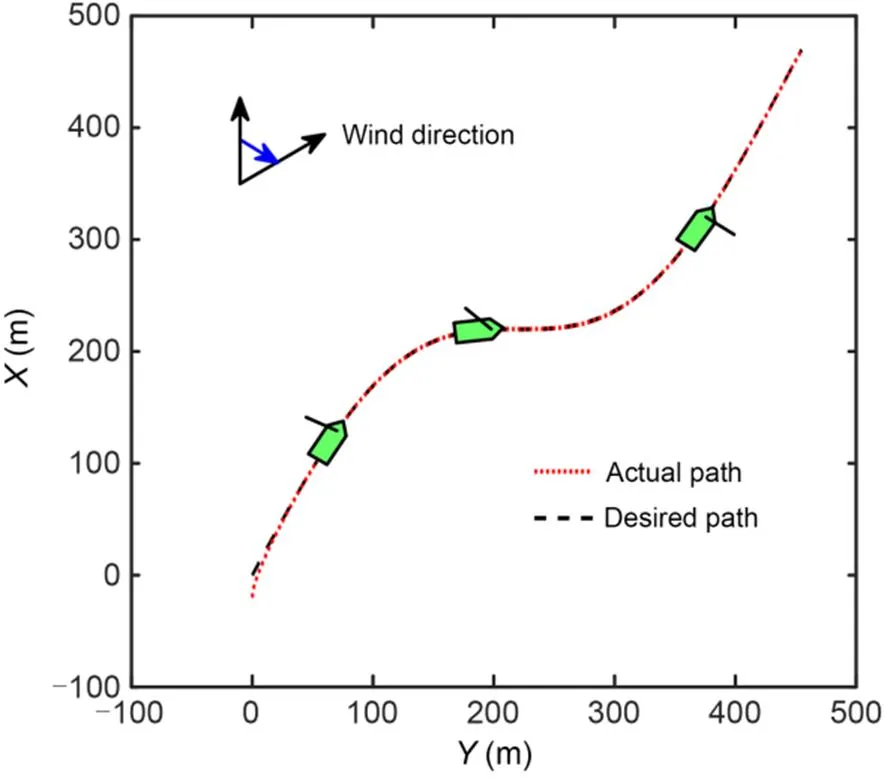
Fig. ‍11 ‍Path following performance of the sailboat of Scheme 2

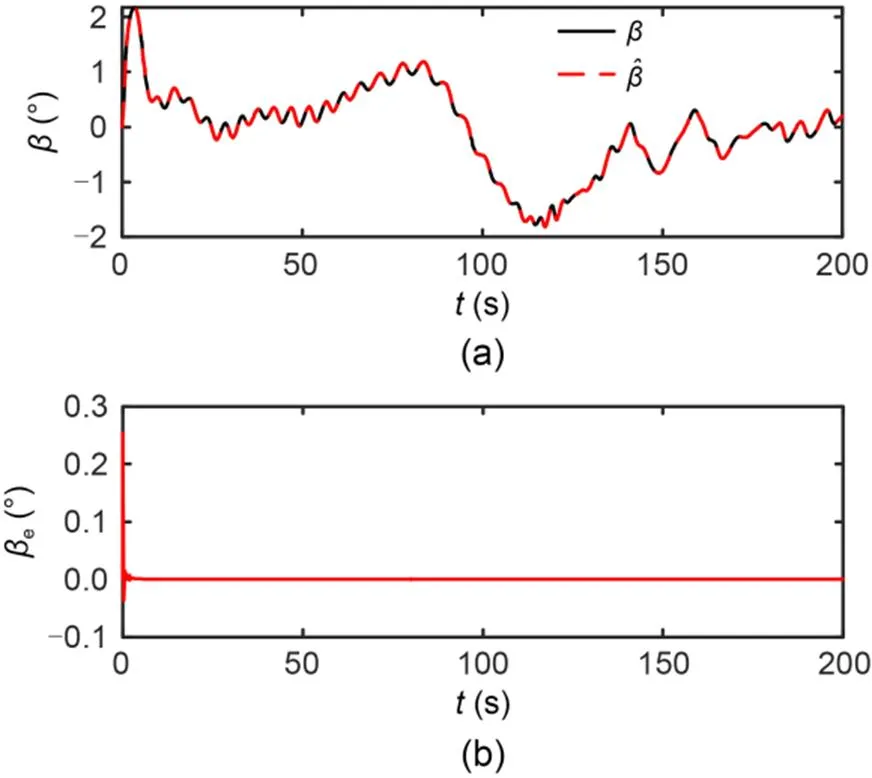
Fig. 13 Estimation (a) and error (b) of the sideslip angle of Scheme 2

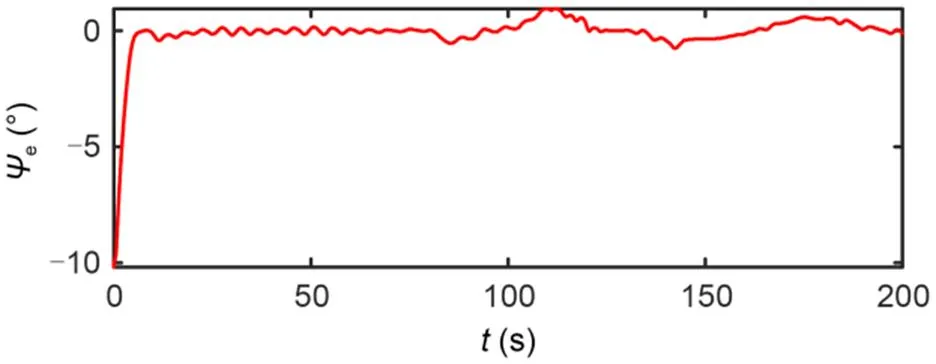
Fig. 14 Heading angle tracking error of Scheme 2

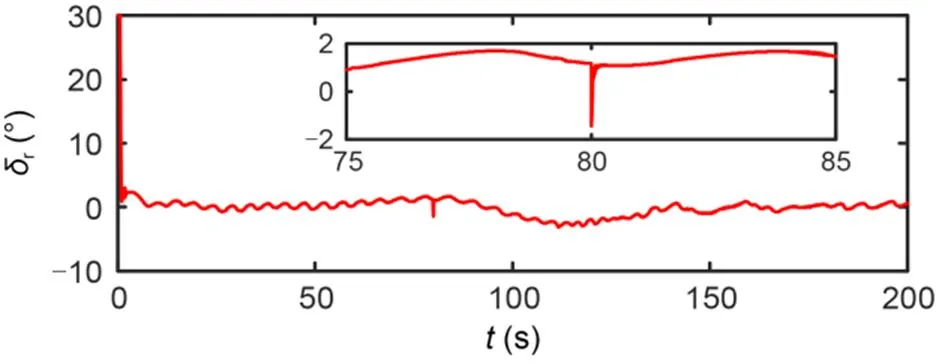
Fig. 15 . Control input of Scheme 2

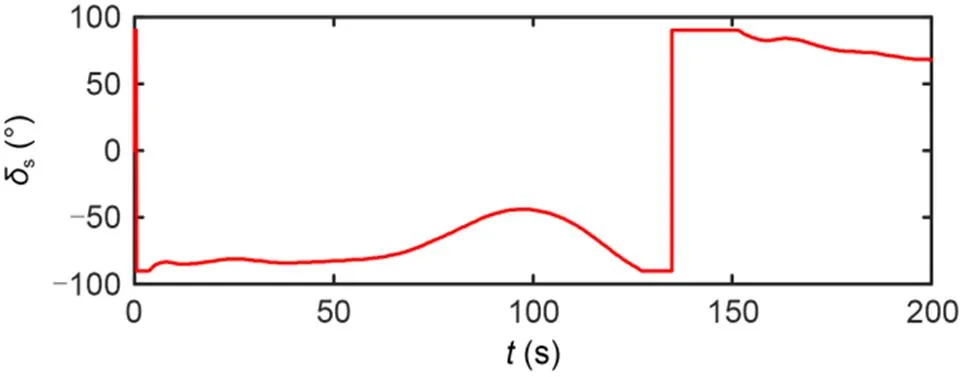
Fig. 16 Control input of Scheme 2

Fig. 17 Variation of sailboat roll angle of Scheme 2

In summary, the overall IDFLOS-FC scheme can achieve exact path following together with accurate sideslip angle observation in the presence of actuator failure, time-varying sideslip angle, and unknown external disturbances.

6 Conclusions

In this study, an IDFLOS-FC scheme was designed to solve the problem of controlling the path following of a USV in the case of actuator failure and under the influence of a time-varying sideslip angle and unknown external disturbance. With the help of DFSO, the time-varying sideslip angle is accurately observed. A sliding model with adaptive parameter adjustment was designed. The sum of fault torque and disturbance force is estimated by an adaptive method, and the uncertain part of the model is estimated by a minimum parameter estimation method. Combining the backstepping method with finite-time theory, a finite-time controller based on DFLOS was established to stabilize the path following error and heading following error in finite-time. Simulation results show that the proposed IDFLOS-FC scheme can achieve accurate path following of an unmanned sailboat under the condition of actuator failure, time-varying sideslip angle, and unknown external disturbance, and can accurately track the desired path when adding faults. These results demonstrate the reliability and superiority of the IDFLOS-FC scheme.

Acknowledgments

This work is supported by the National Natural Science Foundation of China (Nos. 52271306, 52025111, and 51939003), the Central Guidance on Local Science and Technology Development Fund (No. 2023JH6/100100010), and the Fundamental Research Funds for the Central Universities (No. 3132023501), China.

Author contributions

Yujin WU designed the research. Yujin WU and Kangjian SHAO processed the corresponding data. Yujin WU wrote the first draft of the manuscript. Ning WANG and Zhongchao DENG helped to organize the manuscript. Yujin WU and Ning WANG revised and edited the final version.

Conflict of interest

Yujin WU, Kangjian SHAO, Ning WANG, and Zhongchao DENG declare that they have no conflict of interest.

Chen M, Jiang B, Cui RX, 2016. Actuator fault-tolerant control of ocean surface vessels with input saturation., 26(3):542-564. https://doi.org/10.1002/rnc.3324

Cui RX, Zhang X, Cui D, 2016. Adaptive sliding-mode attitude control for autonomous underwater vehicles with input nonlinearities., 123:45-54. https://doi.org/10.1016/j.oceaneng.2016.06.041

Deng YJ, Zhang XK, Zhang GQ, 2020. Line-of-sight-based guidance and adaptive neural path-following control for sailboats., 45(4):1177-1189. https://doi.org/10.1109/JOE.2019.2923502

Dos Santos DH, Goncalves LMG, 2019. A gain-scheduling control strategy and short-term path optimization with genetic algorithm for autonomous navigation of a sailboat robot., 16(1):172988141882183. https://doi.org/10.1177/1729881418821830

Emami SA, Banazadeh A, 2020. Fault-tolerant predictive trajectory tracking of an air vehicle based on acceleration control., 14(5):750-762. https://doi.org/10.1049/iet-cta.2019.0596

Fossen TI, 2011. Handbook of Marine Craft Hydrodynamics and Motion Control. John Wiley & Sons Ltd., Chichester, UK.

Fu MY, Li MY, Xie WB, 2018. Finite-time trajectory tracking fault-tolerant control for surface vessel based on time-varying sliding mode., 6:2425-2433. https://doi.org/10.1109/ACCESS.2017.2783319

Guo B, Chen Y, Zhou AJ, 2021. Event trigger-based adaptive sliding mode fault-tolerant control for dynamic systems., 64(6):169205. https://doi.org/10.1007/s11432-019-2681-1

Hong SM, Ha KN, Kim JY, 2020. Dynamics modeling and motion simulation of USV/UUV with linked underwater cable., 8(5):318. https://doi.org/10.3390/jmse8050318

Li Y, Li XW, Wei XW, 2023. Sim-real joint experimental verification for an unmanned surface vehicle formation strategy based on multi-agent deterministic policy gradient and line of sight guidance., 270:113661. https://doi.org/10.1016/j.oceaneng.2023.113661

Liu T, Dong ZP, Du HW, 2017. Path following control of the underactuated USV based on the improved line-of-sight guidance algorithm., 24(1):3-11. https://doi.org/10.1515/pomr-2017-0001

Liu ZQ, 2022. Improved ELOS based path following control for underactuated surface vessels with roll constraint., 245:110348. https://doi.org/10.1016/j.oceaneng.2021.110348

Liu ZX, Zhang YM, Yu X, et al., 2016. Unmanned surface vehicles: an overview of developments and challenges., 41:71-93. https://doi.org/10.1016/j.arcontrol.2016.04.018

Ma Y, Nie ZQ, Hu SL, et al., 2021. Fault detection filter and controller co-design for unmanned surface vehicles under DoS attacks., 22(3):1422-1434. https://doi.org/10.1109/TITS.2020.2970472

Manley JE, 2008. Unmanned surface vehicles, 15 years of development. OCEANS 2008, p.1-4. https://doi.org/10.1109/OCEANS.2008.5289429

Pettersen KY, Lefeber E, 2001. Way-point tracking control of ships. Proceedings of the 40th IEEE Conference on Decision and Control, p.940-945. https://doi.org/10.1109/CDC.2001.980230

Qin HD, Li CP, Sun YC, 2020. Adaptive neural network-based fault-tolerant trajectory-tracking control of unmanned surface vessels with input saturation and error constraints., 14(5):356-363. https://doi.org/10.1049/iet-its.2019.0221

Shao KJ, Wu YJ, Wang N, et al., 2023. Sailboat path following control based on LOS with sideslip angle observation and finite-time backstepping. S-Cube 2022: Sensor Systems and Software, p.63-78.

Viel C, Vautier U, Wan J, et al., 2018. Position keeping control of an autonomous sailboat., 51(29):14-19. https://doi.org/10.1016/j.ifacol.2018.09.462

Wan L, Cao Y, Sun YC, et al., 2022. Fault-tolerant trajectory tracking control for unmanned surface vehicle with actuator faults based on a fast fixed-time system., 130:79-91. https://doi.org/10.1016/j.isatra.2022.04.013

Wang N, Deng ZC, 2020. Finite-time fault estimator based fault-tolerance control for a surface vehicle with input saturations., 16(2):1172-1181. https://doi.org/10.1109/TII.2019.2930471

Wang N, Ahn CK, 2021. Coordinated trajectory-tracking control of a marine aerial-surface heterogeneous system., 26(6):3198-3210. https://doi.org/10.1109/TMECH.2021.3055450

Wang N, Su SF, 2021. Finite-time unknown observer-based interactive trajectory tracking control of asymmetric underactuated surface vehicles., 29(2):794-803. https://doi.org/10.1109/TCST.2019.2955657

Wang N, Sun Z, Yin JC, et al., 2018. Finite-time observer based guidance and control of underactuated surface vehicles with unknown sideslip angles and disturbances., 6:14059-14070. https://doi.org/10.1109/ACCESS.2018.2797084

Wang N, Gao Y, Zhao H, et al., 2021. Reinforcement learning-based optimal tracking control of an unknown unmanned surface vehicle., 32(7):3034-3045. https://doi.org/10.1109/TNNLS.2020.3009214

Wang N, Zhang YH, Ahn CK, et al., 2022. Autonomous pilot of unmanned surface vehicles: bridging path planning and tracking., 71(3):2358-2374. https://doi.org/10.1109/TVT.2021.3136670

Wang XM, Song XM, Du LH, 2019. Review and application of unmanned surface vehicle in China. The 5th International Conference on Transportation Information and Safety, p.1476-1481. https://doi.org/10.1109/ICTIS.2019.8883835

Wille KL, Hassani V, Sprenger F, 2016. Modeling and course control of sailboats., 49(23):532-539. https://doi.org/10.1016/j.ifacol.2016.10.490

Xia GQ, Wang XW, Zhao B, et al., 2019. LOS guidance law for path following of USV based on sideslip observer., p.1312-1316. https://doi.org/10.1109/CAC48633.2019.8996308

Xiao L, Jouffroy J, 2014. Modeling and nonlinear heading control of sailing yachts., 39(2):256-268. https://doi.org/10.1109/JOE.2013.2247276

Xu MCX, Wang YT, Han ZQ, et al., 2020. Unmanned surface vehicle path following based on path parameter description. Global Oceans: Singapore–U.S. Gulf Coast, p.1-6. https://doi.org/10.1109/IEEECONF38699.2020.9389063

Zhou ZT, Zhong MY, Wang YQ, 2019. Fault diagnosis observer and fault-tolerant control design for unmanned surface vehicles in network environments., 7:173694-173702. https://doi.org/10.1109/ACCESS.2019.2954352

Lemmas S1‍–‍S3

https://doi.org/10.1631/jzus.A2300184

Revision accepted July 8, 2023;

Crosschecked Aug. 28, 2023

© Zhejiang University Press 2023

Apr. 8, 2023;