基于Autoformer 的电力负荷预测与分析研究

唐利涛, 张智勇, 陈 俊, 许林娜, 钟佳晨, 袁培森

（1. 南方电网广西电网有限责任公司计量中心, 南宁 530024;2. 南京农业大学 人工智能学院, 南京 210031）

0 引 言

“双碳”目标的提出, 对智能电网 (smart grid) 的业务智能化提出了新的要求[1]. 新一代智能电网基于现代信息技术与通信技术相结合, 它整合了现代能源技术的高效、智能、安全的电力系统. 此外,该电网架构还能够通过强大的数据分析和实时监控, 有效提升电力数据分析预测的准确性和可靠性[2].

在电力数据预测分析工作中, 负荷预测是其中的关键内容. 负荷预测[3]是指根据电力系统本身的供电决策、天气因素、运行机制等诸多因素, 在满足一定精度要求的条件下, 推算出未来某特定时间点的负荷值, 具有很强的时序特点. 合理预测电力负荷, 一方面可以帮助用户合理用电, 另一方面可以帮助供电方规避效益风险.

目前对于电力负荷的预测研究已初具规模. 杨书强等[4]提出了一种将负荷数据图像化, 并应用长短期记忆 (long short-term memory, LSTM) 人工神经网络进行短期电力负荷预测的方法. 王峰[5]应用改进粒子群优化算法建立了短期电力负荷预测模型. 通过水平方向和垂直方向的平滑修正, 对历史数据的异常负荷点进行识别并修正. 此类研究所遇到的瓶颈问题, 在于两个方面: 一是因为模型适用性不强, 随机森林[6]、支持向量机[7]等算法对于短期数据的周期性拟合较好, 但数据的累积效应[8]会使模型效果变差; 二是由于数据集的精度不够, 大多模拟测试数据集仅对数据进行了惯性增长[9], 与实际生活中用电数据存在偏差, 导致预测结果不能作为精准指标供分配调度.

为克服上述传统预测模型中的问题, 越来越多的学者考虑在时序数据预测中使用基于注意力机制的算法, 主要包括Transformer[10]和Informer[11]. 但由于这些模型直接使用了自注意力机制, 难以从复杂的时间序列模式中找到可靠的时间依赖, 并且由于自注意力机制特有的二次复杂度问题[12], 会限制模型的稀疏度要求, 影响信息利用率. 针对这些问题, 业内提出了Autoformer 模型[13], 它是时序预测在延长预测时效方面的一大突破. 张涛[14]将Autoformer 和非稳态Transformer 引入了电碳因子序列长时预测领域中, 提出了基于多层级潮流追踪的区域动态电碳因子计算框架. 李烈[15]使用Autoformer 方法, 对水位进行了长期预测, 以探索其可行性. 研究证明, Autoformer 可以提高预测精度及效率, 理论上也可运用到具有时序特征的电力负荷数据中, 用以弥补实际电力负荷数据预测工作中的不足.

因此, 本文基于Autoformer 模型, 提出一种电力负荷时序数据预测方法. 该方法对负荷数据进行特性分析后, 在Autoformer 架构上进行改进, 实现负荷预测, 提升电力负荷预测的精确性. 在模型优化过程中, 本文以深度分解架构为整体框架, 能够实现负荷时序数据的深度分解. 同时, 引入自相关机制以增强特征信息的提取能力, 利用网格搜索法进行最佳参数组的寻找, 最终使模型发挥出最好的性能.

1 基于Autoformer 模型的负荷预测框架

1.1 预测整体框架

本文在Autoformer 模型的基础上进行改进, 具体的电力负荷时序数据预测分析框架结构如图1所示, 该框架主要分为5 个部分, 即输入层、特征提取层、编码层、解码层和逻辑回归层.

图1 改进Autoformer 的电力负荷数据预测处理框架Fig. 1 Improving Autoformer’s framework structure for power load data processing and analysis

在图1 中, 输入层将历史电力负荷数据输入到模型中, 负荷序列在经过数据预处理后以集合的形式表示. 在输入层数据进入编码器-解码器部分之前, 序列信息特征要在训练神经网络部分进行充分学习[16].

在特征提取层中, 对负荷数据进行有针对性的特征提取. 具体是利用编码器对负荷序列进行编码,得到序列特征; 同时对负荷序列的周期性信息进行提取和卷积操作, 得到趋势特征[17].

编码层中, 对输入的负荷数据结合提取到的序列特征和趋势进行渐进式序列分解, 寻找更可靠的周期依赖, 将负荷时序数据分解成季节项和趋势项, 作为解码层的输入.

在解码层中进行季节项的渐进式序列分解[18]和周期依赖的寻找, 最后结合编码层输出的趋势项得到未来负荷值的变化趋势, 从而得到解码层的输出.

逻辑回归层由判断结构组成. 当解码层将数据解码后, 判断解码层数是否与设定一致, 若小于则会继续进入下一层解码层进行新的序列分解和预测, 直到解码层数满足要求, 将解码器的输出作为预测结果并重新映射为下一时刻用电负荷的预测概率[19].

1.2 Autoformer 架构

Autoformer 是一个编码器-解码器框架的模型. 编码器和解码器两部分通过序列分解的输入与输出进行相关性连接, 自相关机制和序列分解作为两个独立的模块嵌入到编码器和解码器中. 其模型架构如图2 所示.

图2 基于Autoformer 模型的负荷预测架构Fig. 2 Load forecasting architecture based on the Autoformer model

如图2, 模型分为编码器和解码器两部分. 编码器主要关注负荷周期项, 它的输入是前I时间步,即输入的负荷时间序列. 在自相关机制的控制下, 经过编码器的初步序列分解, 初始输入的时间序列被分解为负荷趋势项和负荷周期项送入解码器. 所以解码器的输入有两部分, 即负荷趋势项和负荷周期项 (在本文场景下, 也可使用负荷季节项), 分别反映长期趋势和周期性, 具体计算公式如式(1)—(2)所示.

式(1)中:χ代表输入时间序列, 对其进行滑动平均 ( A vgPool )[20]处理得到趋势项χt, P adding 操作[21]用来保持序列长度不变.

式(2)中: 输入的原时间序列减去经式(1)处理得到的趋势项之后就得到周期项χs.

送入解码器的负荷季节项和负荷趋势项经过自相关机制的控制进行进一步的序列分解. 解码器分为多个解码层, 每个解码层取时序数据的一段完整数据而不是离散的数据点进行层层序列分解, 实现渐进式的预测, 使预测更可靠也更准确.

解码器包括两个部分, 一个是对编码器输出的趋势项使用累加操作, 逐步从预测的隐变量中提取趋势信息; 另一个是对编码器输出的季节项使用堆叠自相关机制, 进行依赖挖掘并聚合相似子过程.以第1 个解码层χlde为例, 假设有M个解码层, 由于解码层中主要对输入时间序列和编码层输出进行操作, 因此将第一层解码层表示为χlde=Decoder(χld-e1,χNen) . Decoder 表示该表达式为解码层操作, 内部细节如下:

式(3)中: AC 代表自相关机制处理; SD 代表序列分解操作;代表第一次解码的输入时间序列;则是在解码层中解码出来的趋势信息.

Autoformer 基于序列周期性的自相关机制 (Auto-Correlation), 即对输入向量的每个位置的局部区域进行卷积操作, 按照选定的时延对一段时间内的数据选取相似的子过程, 对离散时间过程得到自相关. 自相关系数的计算如式(4)所示.

式(4)中:Rχχ(τ) 为自相关系数, 表示χt和它的t延迟χt-τ之间的相似性;L代表对数据进行延迟操作的次数. 而式(4)表示对于时间序列进行平移, 度量平移前后的时间序列的相似性, 相似性高的平移序列对应的平移量就是潜在的周期. 但是为了提高计算效率, Autoformer 中用快速傅里叶变换[22]计算自相关系数, 具体计算过程如式(5)—(6)所示.

式(5)中:χt为输入的初始时序;F代表傅里叶变换,F∗则是共轭操作;f代表频率, 与2π 相乘得到角频率结果;F和F∗分别对趋势项进行积分得到的结果相乘, 可以将时序转为频域Sχχ.

式(6)中:F-1为傅里叶逆变换, 对式 (5) 得到的结果进行一次傅里叶逆变换得到自相关系数, 这种方法可以降低自相关求解的计算复杂度至O(LlogL) .

2 基于Autoformer 模型的特征提取过程

在负荷预测的任务中, 通过对负荷历史数据和季节特性等参考数据进行特征提取, 可以为模型提供重要的输入特征. 针对复杂的负荷数据, 特征提取阶段的目标是尽可能挖掘丰富的特征信息, 以覆盖多种影响因素.

在负荷数据送入编码器之前, 为了可以提取更多的特征信息, 本文在Autoformer 模型架构中加入特征提取层, 特征提取层主要从序列特征和趋势特征进行提取和融合. 特征提取层框架如图3 所示.

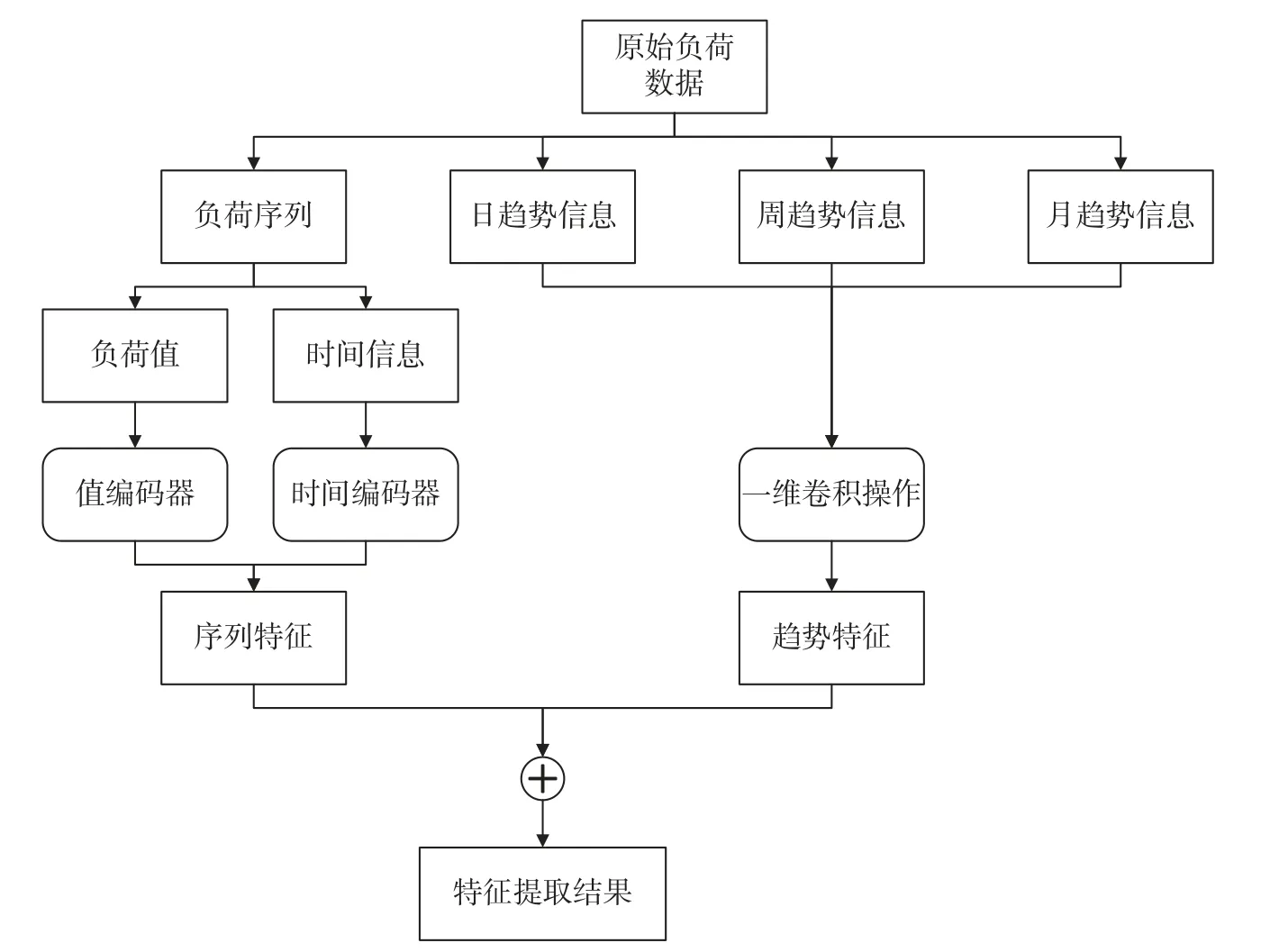
图3 特征提取层框架Fig. 3 Feature extraction layer framework

对于序列特征, 设计了不同的编码器对输入的负荷序列的负荷值以及采集时间进行编码. 首先对负荷序列采用值编码器进行特征映射[23], 另外, 对负荷时序数据中的时间信息也单独采用了时间编码器对时间进行编码, 最后得到的负荷时间序列项处理如式(7)所示.

式(7)中:Ei表示负荷序列的值编码器, 从负荷时序Xi中取一段历史负荷序列进行映射;Ti表示时间编码器, 提取时间信息, 包括月、日、小时、分钟.

对于趋势特征, 首先选取负荷时序数据中过去h个时刻的负荷序列, 在过去h天、h周、h月在t时刻的负荷值, 分别整理成序列集合. 这些序列集合就构成了数据的趋势信息, 可以反映较长一段时间的负荷数据变化趋势及周期性等. 将它们构成趋势矩阵T, 再对这个趋势矩阵进行卷积操作提取负荷序列的趋势特征.

得到序列特征和趋势特征后, 将两类特征进行融合作为特征提取层的输出结果, 融合的过程如式(8)所示.

式(8)中: concat()是常用的连接两个或多个数组的函数,Xt是趋势特征,Xs是序列特征,Xoutput是特征提取的结果.

3 实验结果及分析

3.1 实验环境及数据集

实验平台为Windows10 操作系统, CPU 为AMD Ryzen 5 Gfx 2.10 GHz, 内存16 GB. 本文模型采用PyTorch 1.11.0 和Python 3.10 实现.

使用UCI (University of California Irvine) Tetouan 电力负荷数据集(https://archive.ics.uci.edu/dataset/849/power+consumption+of+tetouan+city). 该数据集包含2017 年1 月1 日0:00 到12 月30 日23:50 的Tetouan 地区电力负荷数据, 每10 min 记录一次负荷值, 共有52 416 个采样点. 数据集有9 个属性, 分别为datetime、temperature、humidity、wind speed、general diffuse flows、diffuse flows、zone 1 power consumption、zone 2 power consumption、zone 3 power consumption. 该数据集包含了Tetouan 地区3 个区的电力负荷数据, 本文中使用其中zone 1 的负荷值作为实验对象, 数据集按8∶2 划分为训练集和验证集.

3.2 数据预处理

针对处理异常值, 本文采用拉格朗日插值法对异常值处的值进行估计和填补, 计算如式(9)所示.

式(9)中:yi表示不同样本点处的因变量;li(x) 是拉格朗日基本多项式, 计算如式(10)所示.

式(10)中:xi和xj表示不同样本点处的自变量.

针对数据归一化, 本文采用的归一化方式是Transformer 中常见的StandardScaler 法进行特征归一化, 如式(11)所示.

式(11)中:xi表示负荷的某个特征值,和s分别代表特征值的均值和方差,yi则是特征值经过标准化之后的标准值.

3.3 评价标准

本文的预测结果采用均方误差 (mean square error, MSE)、平均绝对误差 (mean absolute error,MAE) 和决定系数作为评价指标.

决定系数R2是用来反映模型拟合效果的一种指标, 表示自变量对因变量变化情况的解释能力,如式(12)所示, 一般R2的值越接近1 表示效果越好.

均方误差MSE 用于计算预测值和真实值之间差平方的平均值, MSE 的值越小代表模型的预测表现越好, 其计算公式如式(13)所示.

平均绝对误差MAE 用于计算真实值与预测值之间绝对差的平均值, MAE 的值越小代表模型的预测表现越好, 其计算公式如式(14)所示.

式(12)—(14)中:yi代表第i个样本数据项的真实值,代表使用模型得到的相应的预测值.

3.4 负荷特性结果及分析

本文使用数据集的周负荷特性如图4 所示. 由图4 可知, 一周内每天的电力负荷值变化趋势一致,负荷峰值均出现在工作日, 谷值均出现在周末, 体现出明显的周期性; 且一周内工作日的用电负荷值显著高于周末, 符合负荷特性中的时空性关系.

3.5 实验结果分析

3.5.1 特征提取层结果分析

由于预测中主要考虑负荷值和采集时间两个特征, 因此加入特征提取层对输入负荷时序的序列特征和趋势特征进行提取和融合. 加入特征提取层与不加特征提取层的模型MAE 值、MSE 值和决定系数值如图5 所示.

由图5(a)可知, 加入特征提取层后, 模型在预测进程中的决定系数有所增加, 由图5(b)可知, 在加入特征提取层后, 模型的MAE 值及MSE 值均呈下降趋势. 因此, 加入特征提取层自动从数据中提取特征, 可以使得模型更好地理解数据的规律. 在数据本身可能包含许多不必要的信息的情况下, 自动去除这些无关信息, 使得模型的精度得到提升.

3.5.2 参数优化结果分析

针对本文模型而言, 所需要优化的参数有学习率η、批量大小λ、编码层数α和解码层数β, 下面的结果是对上述参数的寻优结果.

(1) 编码层数及解码层数结果分析

Autoformer 编码层数和解码层数都直接影响着模型的深度和表达能力, 超参数α和β一般选在5 以内. 对编码层数α进行最优值探寻, 固定解码层数β为1, 在此条件下, 编码层数在1—5 时, 模型在预测中的MAE 和MSE 表现如图6 所示.

图6 不同编码层数下模型预测误差Fig. 6 Model prediction error with different number of coding layers

由图6 可知, 随着α的增加, 模型在训练集上的MAE 值及MSE 值变化趋势一致, 当α为3 时,MAE 值及MSE 值同时达到最低. 因此, 本文选α值为3.

对参数β的寻优, 设定α为3,β值在1—5 时, 模型在预测中的MAE 和MSE 结果如图7 所示.

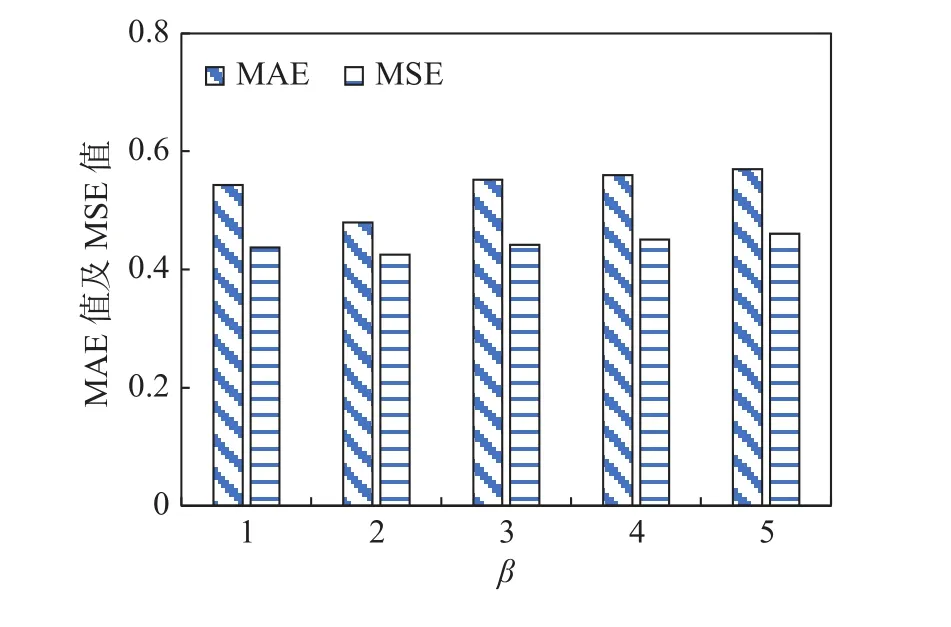
图7 不同解码层数下模型预测误差Fig. 7 Model prediction error under different decoding layers

由图7 可知, 随着β的增加, 模型在训练集上的MAE 值及MSE 值变化趋势一致, 当β为2 时,MAE 值及MSE 值同时达到最低. 因此, 本文选β值为2.

综上, 模型选择设置编码器层数为3、解码器层数为2 进行后续实验.

(2) 学习率结果分析

首先将编码层数设置为3, 解码层数设置为2, 在此条件下进行最优学习率η的寻找.η的范围设置为 1×10-5～1×10-1, 步长为10 倍. 模型在不同学习率预测下的MAE 和MSE 表现如图8 所示.

图8 不同学习率下模型预测误差Fig. 8 Model prediction error under different decoding learning rate

由图8 可知, 随着η的增加, 模型的MAE 值及MSE 值的变化趋势一致, 当η为 1×10-3时, 模型的MAE 和MSE 的值同时达到最低. 因此选取 1×10-3作为模型的学习率进行后续实验.

(3) 批量大小结果分析

批量大小的搜索范围设置在16 ～ 64 之间, 步长设置为16. 不同大小的批量下, 模型在预测中的MAE 和MSE 表现如图9 所示.

图9 不同批量大小下模型预测误差Fig. 9 Model prediction error under different decoding batch sizes

由图9 可知, 在编码层数、解码层数和学习率都最优的条件下, 随着λ的变化, 模型的预测误差变化已经非常小, MAE 值及MSE 值的变化趋势一致, 当λ为32 时, 模型的MAE 和MSE 值达到最低.

(4) 优化器结果分析

本文模型的参数优化对比了Adam 优化器、Adagrad 优化器和RMSprop 优化器. 在不同优化器下, 本文模型的预测结果的MAE 和MSE 如图10 所示.

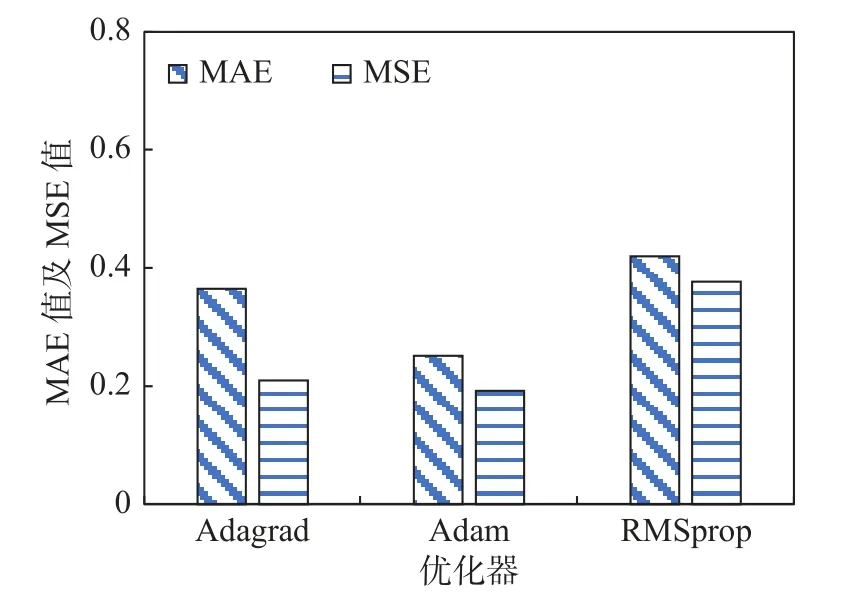
图10 不同优化器下模型预测误差Fig. 10 Model prediction error under different optimizers

由图10 可知, 在最优编码层数解码层数、最优学习率和最优批量大小的条件下, 不同优化器对模型的误差均有不同程度的改善, 当优化器选择Adam 优化器时, 模型的MAE 和MSE 值最低. 因此,选取Adam 优化器作为模型的参数优化器进行后续预测.

综上所述, 寻找到的最优超参数为0.000 1 的学习率、3 层编码器层、2 层解码器层、32 的批量大小, 此时分类准确率达到92.15%, 利用Adam 优化器自适应地调整参数.

3.5.3 预测实验结果

(1) 损失率收敛结果分析

本文迭代轮数设为10 次, 模型在训练集和验证集上的损失率如图11 所示. 图11 (a) 为训练集上的损失率, 随着迭代次数的增加整体呈下降趋势; 图11 (b) 为验证集上损失率随迭代次数的变化趋势, 整体也是下降的, 虽然在迭代次数到达6 时出现了损失率上升的情况, 但在此之后依然呈现平稳下降趋势.

图11 训练集及验证集上损失率随迭代次数的变化Fig. 11 Loss rate on the training and validation sets for different number of iterations

图11 中, 验证集的损失率通常比训练集的损失率高, 这是因为模型在训练过程中可能会出现过拟合的情况, 但是如果验证集的损失率一直上升, 则说明模型出现了过拟合现象, 需要及时调整参数或者增加数据量. 综上, 本文模型在损失率上表现较好, 没有出现过拟合等情况, 保证了负荷预测结果的可信度.

(2) 预测时长变化的结果分析

为分析本文模型在不同时长的负荷预测中的能力, 本文对样本电力负荷进行以天和周为周期的负荷预测, 预测结果如图12 所示.

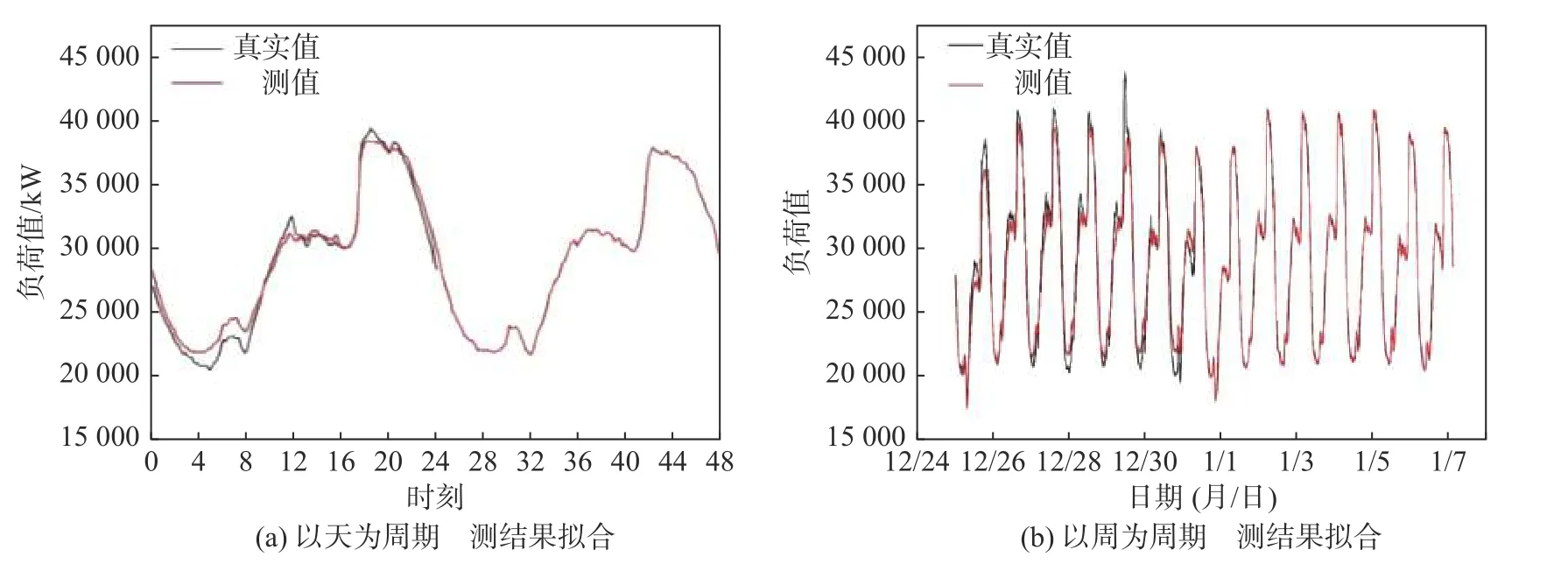
图12 负荷预测结果拟合示例Fig. 12 Example of fitting load forecast results

图12 (a)是2017 年12 月30 日00:00—23:50 该区域的负荷真实值以及2017 年12 月30 日00:00 至2018 年1 月1 日23:50 的负荷预测值. 由图12 (a)可知, 在一天的预测周期内, 真实值和预测值拟合程度较好, 负荷的峰值和谷值出现在一天中的同一时间段内.

图12(b)展示了2017 年12 月24—30 日该区域的负荷真实值以及2017 年12 月24 日至2018 年1 月7 日的负荷预测值. 由图12(b)可知, 本文模型在一周内的预测效果表现良好, 每天的峰值和谷值出现在同一段时间内.

综上, 本文模型在预测中得到的预测值整体趋势与真实值一致, 并且负荷峰值和谷值的出现均在同一时间段内, 具有较优的拟合效果和稳定性.

(3) 本文模型与其他模型预测结果对比

为了对比本文模型的预测性能, 将本文模型与同样基于注意力机制的Transformer 和Informer 进行对比. 为了满足预测效果的要求, 同时减少模型的时耗, 将预测时长设定为一周, 对比结果见表1.

表1 本文模型与其他模型预测效果对比Tab. 1 Comparison of prediction performance with other models

在平均绝对误差上, 本文模型的平均绝对误差控制在0.251 2, 相比Informer 和Transformer 模型分别降低了13.40%和27.17%. 在均方误差上, 本文模型的均方误差控制在0.191 5, 相比Informer 和Transformer 模型分别降低了19.80%和25.24%. 在决定系数上, 本文模型的决定系数达到了0.982 3,分别比Informer 和Transformer 高出了2.18%和6.20%.

综上, 本文使用的改进Autoformer 负荷预测模型在MAE、MSE 和决定系数3 项指标上均得到了显著的改善, 表明本文方法在预测准确性和模型稳定性方面表现出色.

4 结 论

本文在Autoformer 结构基础上, 加入特征提取层提取负荷数据的序列特征和趋势特征, 寻找更可靠的周期性. 在UCI 提供的负荷数据集上, 相比于所对比的其他模型, 本文方法有最佳的MAE、MSE 和决定系数指标, 在电力系统负荷预测方面具有较好的有效性. 此外, 本文方法在不同的预测时长下均具有有效的负荷预测精度.