Aitps：基于非对称模格问题的两方协同签名方案

文嘉明 王后珍,3 刘金会,4 张焕国

1（武汉大学国家网络安全学院 武汉 430072）

2（空天信息安全与可信计算教育部重点实验室（武汉大学） 武汉 430072）

3（密码科学技术国家重点实验室 北京 100878）

4（西北工业大学网络空间安全学院 西安 710072）

（wenjm@whu.edu.cn）

随着互联网的飞速发展，手机等移动设备的适用范围不断扩大.根据中国互联网络信息中心发布的第49 次中国互联网报告[1]，截至2021 年12 月，我国网民规模已达10.32 亿人次，其中即时通信用户规模达10.07 亿人次，网络支付用户规模达9.04 亿人次，网络购物用户规模达8.42 亿人次，在线办公用户规模达4.69 亿人次.移动设备日渐丰富的功能也带来了更严重的隐私信息泄露问题.作为传统签名的替代，数字签名伴随着网络安全的需求出现，为用户提供身份认证和数据完整性认证等，在移动设备的各个功能中发挥重要作用.

然而，数字签名的安全性建立在签名密钥安全的基础上，如果密钥不慎泄露，或者被恶意的网站和应用程序等窃取，可能会出现恶意者冒充等情况，导致隐私信息被滥用、财产损失甚至威胁到国家安全.目前用来保护签名密钥安全的方法主要分为2 种[2]：借助硬件设备令牌保护密钥和使用多方协同签名的思想保护密钥.受限于便利性和成本，前者难以大规模部署到移动设备或物联网设备中；而后者则是由2 个及以上的设备分别存储密钥的一部分，签名时需要多个设备交互完成，任何一方都无法独立地进行签名，分布式的处理能较好地保护密钥安全.

多方协同签名是一种特殊的门限签名，参与签名的用户Pi首先运行密钥生成算法获得私钥ski，然后通过与其余用户的交互生成公钥pk.签名过程也需要交互，对于给定的消息 µ，如果所有的用户都同意对 µ进行签名并诚实参与交互，则交互后得到一个能用pk验证的合法消息签名对 (µ,σ).

尽管多方协同签名协议已经被研究了很长时间，然而现有的大多数工作都集中在多方协同RSA 签名[3-4]、多方协同ECDSA 签名[5-7]、多方协同Schnorr签名[8-10]以及多方协同SM2 签名[2]等，这些方案都基于整数分解或者离散对数困难假设，Shor[11]已经证明了这些困难假设无法抵抗量子计算机的攻击.

相比之下，基于格上的困难假设构造的密码学方案，目前被认为是抗量子的，同时具有运算快、平均情况和最坏情况困难性等价等优点[12]，受到了研究者们的广泛关注.美国国家标准技术研究院（National Institute of Standards and Technology,NIST）举办的抗量子密码（post-quantum cryptography，PQC）征集项目的抗量子密钥封装和数字签名方案，就有相当一部分是基于格的方案，例如CRYSTALS-Dilithium[13]，CRYSTALS-Kyber[14]，Falcon[15]等.中国密码学会在2019 年举办的全国密码算法设计竞赛中的获奖算法大部分也是基于格困难问题构造的，例如Aigisenc/sig[16]和 LAC.PKE[17]等.其中Aigis 设计团队观察到Dilithium 签名方案实际上可以非对称地选择参数，在保证总的重复次数相当的情况下，通过改变前后2 个拒绝抽样的条件及其决定的重复次数，能取得更佳的效果.因而，该团队使用了参数选取更加灵活的非对称模格问题AMLWE/AMSIS（asymmetry module learning with errors/short integer solutions）来代替Dilithium 中的模格问题MLWE/MSIS（module learning with errors/short integer solutions），设计出Aigis-sig 签名方案，在安全性不变或略强的前提下达到更好的综合效果，特别是拥有更短的公钥、私钥和签名长度，具体参见1.5 节.值得一提的是，基于AMLWE/AMSIS的Aigis 方案不仅性能优秀，它还是我国学者自主设计的抗量子密码方案，也已经出现在不同平台上对其实现进行优化的相关工作[18-19].除了提升算法本身和优化实现之外，基于其设计特殊类型签名，例如能更好地保护密钥安全的多方协同签名，对研究国产抗量子密码算法、维护网络安全和国家安全也具有重要的意义.

2019 年，Cozzo 等人[20]对NIST 征集的抗量子数字签名方案中所有进入第2 轮的算法转换成多方协同签名（分布式签名）进行了评估，得出的结论是：如果直接使用已有的安全多方计算的通用技术，基于格的方案将需要用到线性秘密共享和混淆电路等，以及它们之间的互相转换，会带来较大的计算开销，需要较长的时间.

2022 年，Damgard 等人[21]利用Lyubashevsky[22]提出的构造基于格的数字签名的“FSwA（Fiat-Shamir with aborts）”范式，得到了2 个交互轮数较小的基于格的多方协同签名协议（使用加法同态承诺方案需要交互3 轮，使用陷门加法同态承诺方案仅需要交互2 轮），文中的秘密向量是从离散高斯分布中选取的，承诺方案则来自于文献[23]及其扩展方案，该协同签名方案可以看作Dilithium 签名方案的分布式版本，文献[23]中给出了完整的安全性证明，其安全性基于MSIS 问题和MLWE 问题.

Vakarjuk 等人[24]也给出了一个3 轮的两方协同签名方案——Dilizium，与文献[21]中方案的不同之处在于Dilizium 使用SWIFFT 同态Hash 函数[25]替换加法同态承诺方案，虽然得到了更小的密钥和签名尺寸，但是其缺点在于依赖Rejected MLWE 困难假设，是一种启发式的困难假设[26]，同时SWIFFT 同态Hash 函数并不是对所有输入都是加法同态的.现在也已经出现了对具备同态性的Hash 函数的量子攻击方法[27]，这可能会威胁到安全性，尽管如此，我们仍将该方案纳入对比.

此外，文献[21,24]中基于Dilithium 设计的两方协同签名方案均未考虑Dilithium 中用到的签名尺寸压缩技巧[28]，而最新方案Dilizium 2.0[29]采用了类似压缩技术，使其更接近于NIST 标准化的Dilithium 算法，然而该工作并没有评估实际的效率（重复次数）、密钥和签名尺寸等，也未进行参数选取和实例化.

本文的主要贡献包括3 个方面：

1）采用AMSIS/AMLWE 问题对基于MSIS/MLWE问题的Dilizium 2.0 两方协同签名方案进行了修改和推广，得到新方案Aitps.充分利用AMSIS/AMLWE的非对称特性能够更灵活地选择参数，从而在安全性、计算效率、密钥和签名长度这3 个方面达到更好的权衡，得到更优的综合性能.值得注意的是，Aitps方案可以被看作是Dilizium 2.0 方案的一个扩展，在选取适当参数时，Aitps 和Dilizium 2.0 本质上等价，即Dilizium 2.0 可以看成Aitps 的一个特例.除此以外，Dilithium 设计团队和Aigis 设计团队对其方案的后续优化，也适用于本文提出的方案.

2）使用“FSwA”范式构造基于格的多方签名在安全性上需要解决的一个关键问题是防止未通过拒绝抽样时的私钥信息泄露，我们使用同态承诺解决了这个问题（见第2 节）.对于新设计的Aitps 两方协同签名方案，我们提供了完整的安全性证明，结果表明其可以有效保护各方的签名密钥，具备两方协同签名在选择消息攻击下的存在性不可伪造性[5].

3）为了对比效果，本文给出了Aitps 方案的重复次数、密钥和签名大小的评估方法，该评估方法也适用于Dilizium 2.0 方案.我们使用Dilithium 第2 轮的参数[13]和Aigis-sig 的参数[16]将Dilizium 2.0 和Aitps全部进行了实例化，并将Dilizium[24]（其密钥和签名尺寸优于文献[21]）也进行计算并纳入对比，相比之下，本文方案的密钥以及签名尺寸优于现有的所有基于Dilithium 的两方协同签名方案，例如在同等的安全强度下，签名尺寸可缩减20%以上.据我们所知，该结果也是基于格的两方协同签名方案中最优的.

1 预备知识

1.1 符号说明

本文用AT表示矩阵A的转置，Ik表示k阶单位矩阵，「x⏋ 表示大于等于实数x的最小整数，lb 表示以2为底的对数.

R和Rq分别表示多项式环 Z[x]/(xn+1) 和Zq[x]/(xn+1).其中，n为正整数，n-1即为环中的多项式的最高次数，实际方案中一般选取n为2 的幂次（例如n=256）；q表示环Rq的模数，一般选取较大的素数，在选取时需要综合考虑方案的其他参数和工程实现的效率.表1 给出了一套具体参数的例子.

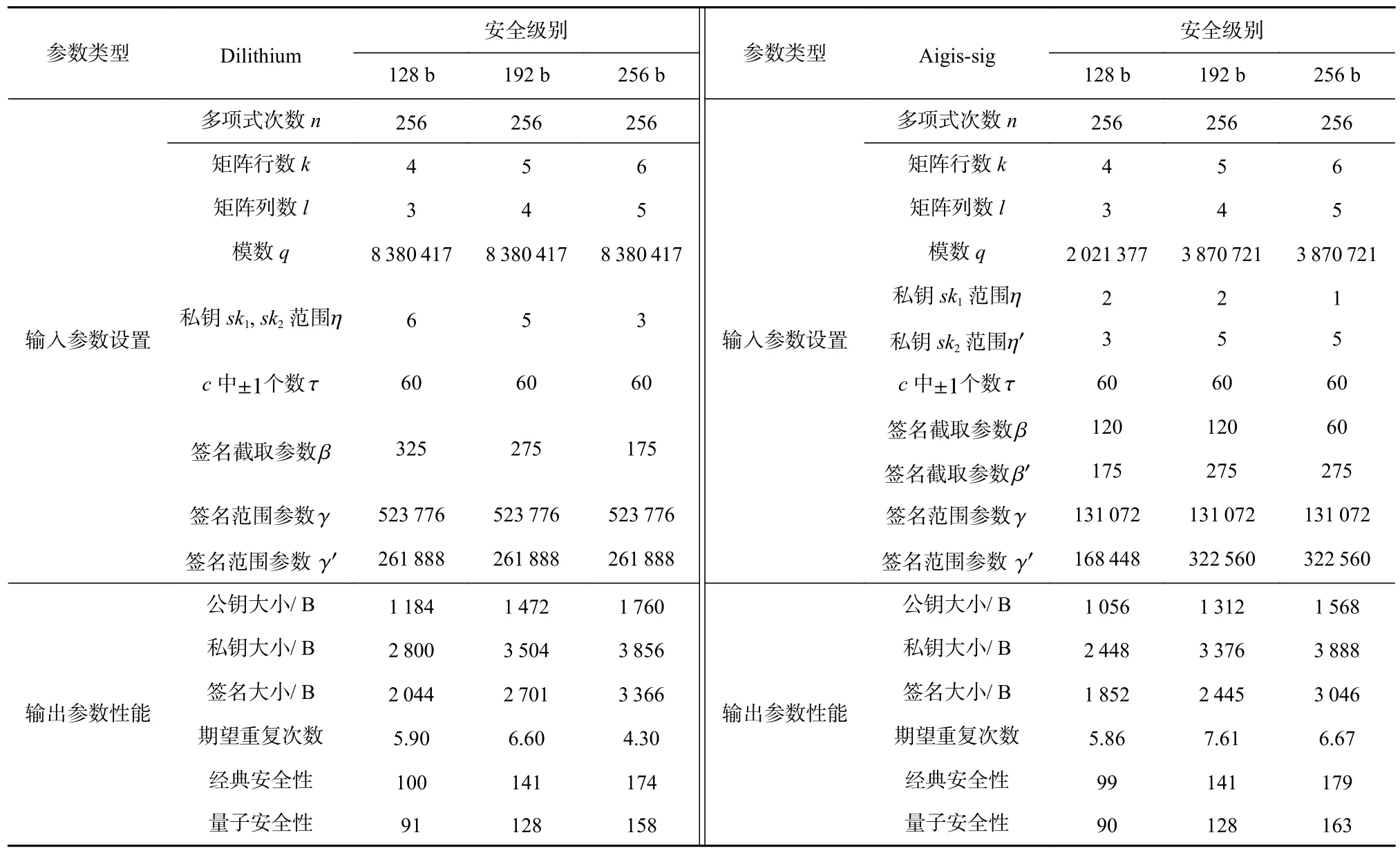
Table 1 Recommended Parameters of Dilithium and Aigis-sig表1 Dilithium 和Aigis-sig 的推荐参数

对于η>0，用Sη表示由所有的满足‖w‖∞≤η的多项式w∈R（或Rq）组成的集合.

对于集合（或分布）D，用x←$D表示从集合（或按照分布）D中均匀随机选取x.

1.2 格上的困难问题

本文直接采用正规型（A）MLWE/（A）MSIS 问题及假设，定义如下.

由D3中的(A;t)恢复(s1;s2)称为计算性AMLWE问题（computational AMLWE），区分2 个分布D3和D4中的(A,t)称为判定性AMLWE 问题（decisional AMLWE）.

Zhang 等人[16]已经证明，对于目前已知最好的求解算法，有困难性关系：

1.3 （同态）承诺方案

承诺方案最早由Chor 等人[31]在研究可验证的秘密分享时提出，现在已经被用在各种特殊类型签名中，例如环签名[32-33]、群签名[34]等.在承诺方案中，对于给定的消息m∈Sm，承诺者选择随机向量r∈Sr用来计算m的承诺值com=Commitck(m;r)，其中ck∈Sck是承诺密钥，并将承诺值com发送给接收者.在承诺打开阶段，承诺者将与承诺值相关的信息发送给接收者，接收者能利用承诺值以及相关信息计算得到一个打开值（opening），并验证其确实是最初承诺的消息值.

除了具备正确性之外，承诺方案还需要具备隐藏性和绑定性2 个安全属性.

1）隐藏性（hiding）指的是承诺值不会泄露被承诺值的任何信息，即通过com=Commitck(m;r)无法得到关于m或r的信息.

2）绑定性（binding）指的是打开一个承诺不能得到2 个不同的值，即打开com=Commitck(m;r)得到(m′,r′)，则 (m′,r′)≠(m,r)的概率是可忽略的.

根据敌手的能力和计算时间进行分类：若敌手拥有无限计算时间与资源则称为统计隐藏性（绑定性），若限制在多项式时间则称为计算隐藏性（绑定性）.

在满足正确性和安全性后，该承诺方案还具备3个性质[21]：

1）密钥均匀性（uniform key）.产生承诺密钥的算法得到的承诺密钥ck∈Sck在 Sck上均匀分布.

2）ξ-bits 最小熵.称一个承诺方案至少有 ξ-bits最小熵，如果对于 ∀ck∈Sck和 ∀m∈Sm，均有

3）加法同态性.对于任意的m1,m2∈Sm以及随机数r1,r2∈Sr，计算得到com1=Commitck(m1;r1)和com2=Commitck(m2;r2)，满足加法同态性，即

1.4 CRYSTALS-Dilithium 数字签名方案

2022 年7 月，NIST 宣布了PQC 项目第3 轮的评审结果[36]，确定了4 种即将标准化的算法，其中最为推荐的是CRYSTALS-Kyber（密钥封装）和 CRYSTALSDilithium（数字签名），此外，另一个基于格的签名方案Falcon 和基于Hash 的签名方案SPHINCS+[37]也将标准化.在数字签名方面，根据设计团队向NIST 提交的材料以及官方评价显示，Falcon 是利用“Hashand-Sign”范式构造，虽然拥有更短的尺寸，但其签名算法内部逻辑较复杂，实现难度较大；SPHINCS+是一类基于Hash 的无状态签名方案，其安全性依赖于底层Hash 函数的安全性，提供可靠的安全保证，然而会导致性能上的巨大成本.相对而言，Dilithium 拥有很强的安全性和优秀的性能，能胜任绝大多数场景需求.

Dilithium 是一类基于格上的困难问题构造的数字签名算法，算法的设计用到了“Fiat-Shamir with Aborts”范式，并使用了一些压缩技巧[28,38]，主要具备3 个优点[13]：

1）容易安全地实现.此前的基于格的数字签名方案[39-40]等需要从离散高斯分布中抽样得到秘密值，效率较低，还容易遭到侧信道攻击而导致实现的不安全[41-42].与它们不同，Dilithium 签名方案只需要进行均匀抽样，且除了抽样之外，其余的运算操作（例如多项式乘法和舍入）都可以在恒定时间内完成，这有利于增强实现上的安全性.

2）公钥+签名尺寸优.为了能长期使用，Dilithium团队提交给NIST 的参数选取非常保守，即便如此，Dilithium 方案的“公钥+签名”的尺寸也是现有的不使用离散高斯抽样的格签名方案中最小的.

3）模块化切换.只需在环上进行更多或更少的操作，或者修改其中所用的可扩展输出长度Hash 函数（XOF，推荐使用SHAKE-128 或SHAKE-256）就可以切换不同级别的安全性.换句话说，一旦获得某个安全级别的更优化实现，就很容易获得其他安全级别的更优化的实现.

将Decomposeq(·)算法作用于多项式（例如环Rq中的元素）或由多项式组成的向量、矩阵时，表示对应操作被分别独立地作用到多项式的每个系数.使用Decomposeq(·)算法，能对任意的由Rq中的多项式组成的向量 Θ和小范数向量 Λ，在不保存 Θ的情况下恢复Θ+Λ的高位比特，其正确性由引理1 保证：

引理1[13].Θ,Λ 是由Rq中的多项式组成的向量，ρ1和 ρ2是正整数，如果 ‖Λ‖∞≤ρ2且 ‖LowBitsq(Θ,ρ1)‖∞<则等式HighBitsq(Θ,ρ1)=HighBitsq(Θ+Λ,ρ1)成立.

Dilithium 签名方案包括3 个子算法：密钥生成算法、签名算法和验证算法，这里介绍不考虑压缩公钥t的简化版本.

1）密钥生成算法.首先使用种子生成矩阵A，然后均匀随机选取sk1=s1←$,sk2=s2←$并计算t=As1+s2，公钥pk=(A,t)，私钥sk=(A,t,s1,s2).

算法1.Dilithium-签名算法.

3）验证算法.在得到 µ和 σ=(z,c)后，首先利用Decomposeq(·)算法计算Az-ct的高位比特，然后根据z的范围和挑战值c的正确性判断签名合法性.

算法2.Dilithium-验证算法.

更详细的Dilithium 签名方案的正确性以及安全性分析参见文献[13].

1.5 Aigis-sig 数字签名方案

2020 年1 月，中国密码学会发布了全国密码算法设计竞赛的结果，Aigis-sig 数字签名方案是公钥密码组获得一等奖的3 个方案中唯一的签名方案，并且其对应的密钥封装方案Aigis-enc 同样也获得了一等奖，在国内抗量子公钥密码设计中具有高度评价，经过进一步的改进后，将成为我国自主设计的重要抗量子密码方案.

Aigis-sig 的主要设计思想与Dilithium 类似，改进之处在于使用了更加灵活的非对称的格上困难问题——AMSIS 问题和AMLWE 问题，通过改变私钥s2的选取范围以及拒绝抽样的条件，得到了更优的公钥尺寸或签名尺寸，以及更强的安全性.Aigis-sig 签名方案包括3 个子算法：密钥生成算法、签名算法和验证算法，这里介绍不考虑压缩公钥t的简化版本.

1）密钥生成算法.首先使用种子生成矩阵A，然后均匀随机选取sk1=s1←$,sk2=s2←$并计算t=As1+s2，公钥pk=(A,t)，私钥sk=(A,t,s1,s2).

算法3.Aigis-sig-签名算法.

3）验证算法.在得到 µ和 σ=(z,c)后，首先利用Decomposeq(·)算法计算Az-ct的高位比特，然后根据z的范围和挑战值c的正确性判断签名合法性，这里的 β（以及未显式表达的 β′）与算法2 中的 β不同.

算法4.Aigis-sig-验证算法.

2 两方协同签名方案

本文基于AMSIS/AMLWE 困难问题提出的两方协同签名方案有2 个.

2）签名算法.我们以用户P1的视角为例介绍两方协同签名协议，对消息 µ∈M进行签名的具体过程如图1 所示，运行协议后得到z1.同样地，P2也会得到z2，将两者合起来即得到签名 σ=(z,c,h).

和Dilithium 一样，签名算法的第1 步是计算身份协议所需要用到的挑战值c∈C=Bτ（Bτ的定义与文献[13,16]相同，表示环R中恰好有 τ 个系数为 ±1且其余系数为 0的元素组成的集合），该值应该由双方一起生成，因而需要双方交换多个消息，但是并不能直接交换w1和w2（或其对应的高位比特），主要原因有2 个方面：

①如果P1将w1发 送给了P2，而之后未通过拒绝抽样，签名过程中止，(w1,z1) 可能会泄露关于私钥sk1,1的信息.之前的工作[26]的解决方法是利用非标准的格困难假设——Rejected MLWE 假设，然而这只是一个启发式假设，可能存在安全性问题.

②如果P2知道了 (w1,z1)，可以从z1中提取得到c·sk1,2从而得到P1的私钥的一部分sk1,2，P1同理，这也可能会导致安全性上的威胁.

我们用同态承诺方案来解决这个问题.P1和P2均可以用公钥pk=(A,t) 和消息 µ计算得到消息对应的承诺密钥ck←Hck(µ,pk)，先互相交换承诺值comi=Commitck(wi,H;ri)，由于使用的是同态承诺，因此可以将不同用户的承诺值聚合在一起，并用来在签名生成阶段计算挑战值.同时和密钥生成算法一样，在互相交换承诺值comi之前需要先交换承诺值对应的Hash 值H3(comi)，如果缺少了这一步，恶意的P2可以在看到P1的承诺值com1自适应地选择com2′.

在第3 轮通信中，双方交换 (zi,ri).并验证对方提供的comi是否确实是用同态承诺方案计算得到，验证通过后，计算得到完整的z=z1+z2.

3）验证算法.收到消息 µ对应的签名σ=(z,c,h)以及用来计算承诺的r，作如下验证.

1）验证 ‖z‖∞<2γ-2β.

2）用公钥pk=(A,t) 和消息 µ计算得到消息对应的承诺密钥ck←Hck(µ,pk).

5）验证c=H0(µ,com)，若通过，返回1（即接受签名），否则返回0（即拒绝签名）.

2.1 方案的正确性分析

证明本文提出方案的正确性，实际上就是证明3个结论：

同时根据由签名算法的定义得到LowBitsq(Azct,4γ′)<2γ′-2β′，由引理1 有

3）Openck(com,,r)=1

由于com是在签名算法中通过成功运行“挑战值计算阶段”以及承诺方案的加法同态性质生成的，因此有

是w1,H+w2,H对应的一个承诺值，即为对应的一个承诺.

验证方计算得到wH=HighBitsq(Az-ct,4γ′)和签名算法是相同的，再利用h=wH-进行“纠正”得到，因此有Openck(com,,r)=1.

2.2 方案的安全性分析

本节给出两方协同签名的安全性定义以及本文所提方案的安全性证明.和文献[21]一样，我们沿用Lindell 给出的两方协同签名的基于游戏的安全性定义[5]，在该定义中，假设敌手只能调用一次密钥生成算法，而多个签名会话可以同时执行.

我们证明本文提出的两方协同签名方案具有分布式签名的选择消息攻击下的存在性不可伪造性（distributed signature with existential unforgeability under chosen message attack,DS-EU-CMA），需要用到如下的实验ExpDS-EU-CMA(A)：

初始时定义签名消息集合 M为空集，敌手可以询问协同签名的谕言机 ODS，得到若干个消息签名对(µi,σi)，并将 µi添加到 M中，最后敌手需要产生一个新的 (µ∗,σ∗)，其中 µ∗≠µi.

两方协同签名方案DS-EU-CMA 安全意味着对于任意概率多项式时间的敌手 A，成功伪造签名的优势AdvDS-EU-CMA(A)是可忽略的，其中优势的定义为

我们的安全证明的主要思想与文献[21,29]类似，我们证明了：如果敌手能以不可忽略的概率成功进行一个有效的伪造，则可以攻破承诺方案的计算绑定性或者AMLWE/AMSIS 假设，即能以概率 εBinding攻破承诺方案的计算绑定性，或能以概率解决参数为 (q,k,l,η,η′)的判定性AMLWE 问题，或能以概率解决参数为 (q,k,l+1,δ,δ′)的AMSIS 问题，其中 ε均表示不可忽略的概率值.证明过程中需要用到文献[44]提出的分叉引理，在此先进行介绍.

引理2.分叉引理（general forking lemma）[44].对于固定的询问次数Q≥1以及集合 H（H中的元素个数|H|≥2），令 B是一个随机化算法，满足(i,σout)←B(x,h1,h2,…,hQ)，其输入 h1,h2,…,hQ∈H,x是由一个随机化的输入值生成算法 IG产生，输出i∈{0,1,…,Q},σout是一个辅助输出.

FB(x)是与 B相关联的分叉算法，定义为：

1）B 选取 ρ作为随机的硬币（coins），以随机化.

2）随机选取 h1,h2,…,hQ←$H.

3）运行算法 B：(i,σout)←B(x,h1,h2,…,hQ;ρ).

定义 B的接受概率acc和分叉概率frk.

在本方案中，定义IG 的输出为(A,t,ck∗).

定理1.假设承诺方案具有计算隐藏性、计算绑定性、密钥均匀性、加法同态性和 ξ-bits 最小熵.那么对于任意的可以询问1 次密钥生成随机谕言机，QS次签名谕言机和QH次随机谕言机H0,H1,H2,H3,Hck的概率多项式时间敌手，该两方协同签名方案是DSEU-CMA 安全的，其安全性依赖于参数为(q,k,l,η,η′)的AMLWE 假设以及参数为 (q,k,l+1,δ,δ′)的AMSIS假设.

证明.对于一个能攻破该两方协同签名方案的敌手 A，我们首先构造一个关于 A 的模拟器 S，能在不使用诚实用户的密钥的前提下模拟协议中诚实用户Pn的行为.S 用到了S imKeyGen(·) 及S imS ign(·)谕言机[21,29].我们通过一系列的中间游戏Gamei来定义 S，并比较了每一个游戏和前一个游戏的差别.在得到S 后，我们利用 S 构造了算法 B，并通过调用分叉引理获得针对2 个不同的挑战值的伪造签名，这使得我们能攻破承诺方案的计算绑定性或者AMLWE/AMSIS 假设.

Game0：分为随机谕言机模拟（random oracle simulation）、诚实用户谕言机模拟和伪造3 个部分.

1）随机谕言机模拟.本方案中用到5 个Hash 函数H0,H1,H2,H3,Hck，分别模拟：

①H1:{0,1}∗→{0,1}l1（用在密钥生成算法中的公钥矩阵生成）.构造空的Hash 列表HT1，当向HT1询问x′时，若列表中已经有HT1(x′) 则返回HT1(x′)，否则从{0,1}l1中均匀随机地选取一个值y′当作HT1(x′)，并将(x′,y′)填入HT1.

②H2:{0,1}∗→{0,1}l2（用在密钥生成算法中的私钥和t的生成）.构造空的Hash 列表HT2，当向HT2询问x′时，若列表中已经有HT2(x′) 则返回HT2(x′)，否则从 {0,1}l2中均匀随机地选取一个值y′当作HT2(x′)，并将 (x′,y′)填入HT2.

③H3:{0,1}∗→{0,1}l3（用在签名算法中的交换承诺值）.构造空的Hash 列表HT3，当向HT3询问x′时，若列表中已经有HT3(x′) 则返回HT3(x′)，否则从{0,1}l3中均匀随机地选取一个值y′当作HT3(x′)，并将(x′,y′)填入HT3.

④H0:{0,1}∗→C（用在签名算法中的计算挑战值）.构造空的Hash 列表HT0，并令ctr=0.注意到H0的输入为 (µ,com)，因此需要先询问随机谕言机H3(µ,pk)，若列表中已经有HT0(µ,com)则返回HT0(µ,com)，否则设ctr=ctr+1，并将 hctr当作HT0(µ,com)，将(µ,com,hctr)填入HT0.其中，{h1,h2,…,hQS+QH+1}是 S收到的作为输入的随机挑战值.

⑤Hck:{0,1}∗→Sck（用在计算承诺密钥）.构造空的Hash 列表Hck，由于Hck的输入为 (µ,pk)，故向HTck询问 (µ,pk)，若列表中已经有HTck(µ,pk)，则返回HTck(µ,pk)，否则从承诺密钥空间 Sck中均匀随机地选取一个值y当作HTck(µ,pk)，并将 (µ,pk,y)填入HTck.

搜索Hash 列表算法S earchHash(HT,h).在构造Hash 列表HT后，可以定义算法S earchHash(HT,h):对于h，在列表HT中寻找原像满足HT()=h，如果不存在原像，则返回flag=alert 并设置m=⊥，如果存在不止一个原像，则返回flag=bad.

2）诚实用户谕言机模拟（honest party oracle simulation）.在这个游戏中，敌手 A的行为和两方协同签名中的一个诚实用户相同.与文献[21,29]类似，当A询问诚实用户谕言机时，S可以直接按照密钥生成算法和签名算法的定义进行模拟，限于篇幅，在此处不展开，感兴趣的读者可以参见文献[21,29].

3）伪造（forgery）.敌手 A输出一个伪造的消息签名对 (µ∗,σ∗=(z∗,c∗,h∗)).对于给定的伪造，S操作为：

将 S 在第i个游戏中不输出 (0,⊥)的概率记作Pr[Gamei]，有Pr[Game0]:=AdvDS-EU-CMA(A).

Game1: 相较于Game0，Game1仅改变 S的签名过程，主要的变化在于挑战值c改为从集合 C中均匀随机选取，因此 S能在不与敌手 A交互的情况下计算出zn.在收到挑战值 hi后，S运行搜索Hash 列表算法S earchHash(HT3,hi)，找到原像comi并计算com=comn+comi，最后，S 用c当作对随机谕言机H0的询问(µ,com)的回答.除了3 种情况之外，Game1和Game0是等同的.

和之前的游戏一样，S将wn,H进行承诺得到comn=Commitck(wn,H,rn)，其中rn←$Sr，并将H3(comn)发送给敌手 A.

Game2和Game1之间的区别是 A 在进行QS次询问后，区分一个模拟的承诺方案和一个真实的承诺方案的优势不同，即攻破承诺方案的隐藏性的优势不同.因此有 |Pr[Game2]-Pr[Game1]|≤QS·εHiding.

因此，若敌手以不可忽略的概率成功伪造签名，则能以不可忽略的概率攻破承诺方案的计算绑定性或AMLWE/AMSIS 假设.证毕.

3 性能分析与比较

为密码方案选择合适的参数需要在多个方面权衡，本方案参数的选择应该在保证足够安全性的前提下，使得期望重复次数（影响通信轮数和签名时间）较小且拥有较短的签名和密钥尺寸，因此我们主要考虑这3 项指标，并以此评价方案的性能.

3.1 重复次数的期望值（通信重复轮数）

3.2 密钥和签名大小

这里和文献[24]一样，由于ski,1和ski,2的每个系数都可能是负的元素，因此需要额外1b 来表示符号.

3）计算签名大小.签名由(z,c,h)共3 个部分组成：

z是一个l维向量，且满足 ‖z‖∞≤2(γ-β)-1，因此z的大小约为n·l·(「lb((γ-β)-1)⏋+1).

c是挑战值，和文献[13,16,22]选取自相同的挑战值集合，因此c的大小为 τ·(「lbn⏋+1).

综上，签名（单位B）共需要约

特别地，当 η′=η,β′=β时，本文的方案与Dilizium2.0两方协同签名方案本质上等价，也就是说Dilizium 2.0 可以视为本文方案的一个特例.

我们选取Dilithium 第2 轮的参数[13]以及Aigis相对应的参数[16]进行实例化，参数如表1 所示，得到的密钥大小和签名大小的对比见表2，签名成功所需重复次数的对比见表3.

Table 3 Comparison in Expect Repeations表3 期望重复次数比较

由表2 可知，我们提出的两方协同签名方案比文献[24,29]拥有更短的密钥和签名.而在决定运行时间的期望重复次数方面，虽然大于文献[29]的方案，但由文献[16]和表3 可知，即使重复次数略大，在进行工程上的优化以及使用AVX2 进行加速后，Aigissig 甚至在一些参数下快于Dilithium（具体运行时间对比参见文献[16]），因此我们合理地认为实际情况下Aitps（本文提出的基于Aigis-sig 的两方协同签名方案）与Dilizium 2.0（现有最优的基于Dilithium 的两方协同签名方案）效率相当.

4 总结及展望

本文提出的Aitps 是一种基于格的两方协同签名协议，允许2 个用户在不泄露各自私钥的情况下通过交互对给定的消息进行签名，同时任何一方都无法重构密钥和独自完成整个签名过程，保证了密钥的安全性.在协议的安全性方面，我们将其归约到非对称模格困难问题以及用到的承诺方案的计算隐藏性（本质上也是基于模格问题的困难性）.由于现有的最优的相关方案Dilizium 2.0 没有评估效果，我们也给出了Aitps 方案各项评价指标的计算公式（也适用于Dilizium 2.0 方案），并采用CRYSTALSDilithium 和Aigis-sig 的推荐参数进行实例化，相比之下，本文提出的方案比现有的所有基于Dilithium 的两方签名方案具有更小的密钥和签名尺寸，特别是签名尺寸，能减少至少20%.

与文献[21]一样，本文提出的两方协同签名方案很容易扩展成为安全的多方协同签名方案.在未来的工作中，我们将进一步考虑使用提交给NIST 的CRYSTALS-Dilithium 签名方案中对公钥的压缩技巧继续减小公钥尺寸，以及尝试降低期望重复次数.

作者贡献声明：文嘉明提出算法设计思路并撰写论文；王后珍提出算法优化及分析思路，并参与撰写论文；刘金会和张焕国提出指导意见并修改论文.