基于高预测性的稀疏矩阵向量乘法并行计算优化

夏 天 付格林 曲劭儒 罗中沛 任鹏举

1（人机混合增强智能全国重点实验室（西安交通大学） 西安 710049）

2（视觉信息与应用国家工程研究中心（西安交通大学） 西安 710049）

3（西安交通大学人工智能与机器人研究所 西安 710049）

（pengjuren@xjtu.edu.cn）

在科学计算、大数据分析和智能计算任务中，稀疏矩阵向量乘法（sparse matrix-vector multiplication，SpMV）是广泛使用的计算核心.例如，在大数据推荐系统[1]和图神经网络[2-4]中，通常会对图邻接矩阵进行迭代的矩阵向量乘法来完成大规模的节点信息汇总和传播，如在经典的Pagerank 算法中，不同网页之前的关联度用稀疏矩阵表示，通过对稀疏矩阵做多次SpMV 迭代计算，能求解不同网页的排序关系；而在现代科学计算任务的数值模拟计算中，也经常使用迭代法来进行大规模稀疏线性方程组的求解.在以上计算任务中，SpMV 构成了主要的计算负载，其计算性能直接影响了整体算法的解算效率.因此，提升SpMV 的计算性能对于优化许多科学计算和智能计算任务性能具有重要意义.

与此同时，基于超标量和乱序技术的现代处理器架构高度依赖计算与访存模式的规则化和可预测性来充分发挥其计算性能.具体来说，现代处理器通常依赖准确的分支预测技术来提升其流水线执行效率，并且采用高效的数据预取技术来有效掩盖访存延迟，分支预测技术和数据预取技术均需要计算程序在控制跳转和数据访问行为上呈现高度的可预测性.此外，数据访问的时间局部性与空间局部性直接影响缓存的使用效率，对处理器性能也至关重要.然而在SpMV 中，稀疏矩阵通常具有极高的稀疏率，非零元素的占比通常低于0.01%，并且其分布通常是随机的，并无规律可循.这就导致在计算过程中对于向量元素的索引和访问呈现出高度不规则性，缺乏访存局部性，严重制约了缓存和访存带宽的使用效率[5].与此同时，由于矩阵中每行的非零元素数量不同，也导致了分支预测和并行化计算的困难.这些因素导致了SpMV 在很多算法中构成了严重的性能瓶颈.因此，SpMV 在现代处理器上的设计与优化至今仍然是研究热点和亟需解决的问题.

目前，对于SpMV 的研究成果已有很多，其中很多工作注重提升计算并行度以适配SIMD（singleinstruction-multiple-data）和SIMT 等并行计算技术[6-9].还有一些工作通过进行矩阵的分块计算来提升数据的局部性[10-14].然而，这些工作只局限在某个单一维度上，而缺乏对于整体算法的协同优化，因此可能造成整体的优化效果受到制约.例如，基于分块方法的数据局部性提升经常会导致程序复杂度的上升，可能会带来指令数的增加，从而导致核心的计算指令密度下降、计算效率被削弱.此外，现有研究工作中对于分支预测和数据预取等可预测的计算特性如何影响性能仍然缺乏充分的讨论和优化.

本文通过研究，总结出制约SpMV 性能的3 个关键因素：高访存延迟、低分支预测准确率以及低代码计算密度.针对这些问题，本文构建了一种新型的SpMV 计算方法——pvSpMV（predictable vectorized SpMV）.该方法通过对稀疏矩阵的数据结构重组以及向量元素的位置重组，实现了程序控制流和访存行为的高预测性，从而充分发掘乱序处理器流水线和数据预取的执行效率；在此基础上，通过对程序复杂度的降低和向量化程度的提升，显著优化代码计算密度，从而实现对于SpMV 的全面提升和性能优化.本文还基于SuiteSparse[15]稀疏矩阵测试集评估pvSpMV 性能，测试结果显示，pvSpMV 可以在主流Intel 高性能处理器上获得与主流商用计算库MKL相比平均2.6 倍的加速比，相比于现有最先进算法获得平均1.3 倍的加速比.此外，pvSpMV 所需的预处理开销较低，预期可以在迭代计算中被有效分摊，从而不影响整体算法的性能提升.

本文的主要贡献包括4 个方面：

1）构建一种访存模式可预测的SpMV 表示方法pvSpMV，可以高效适配数据预取器，大幅度提升取数带宽，并且提升缓存的利用效率；

2）在此基础上，分析SpMV 中的关键分支跳转指令，并且提出一种分支跳转可预测的稀疏矩阵数据存储结构，提升处理器的执行效率；

3）定义用于衡量程序效率的有效计算指令密度的性能指标，并且以此指标为基础，设计一种采用极低程序复杂度完成的高效SIMD 计算方法，提升有效计算指令密度；

4）采用来自多种领域的稀疏矩阵开展了充分实验，并且与现有的先进方法进行对比，结果表明pvSpMV 可以有效缓解SpMV 问题中的多个关键性能瓶颈，具有较好的性能收益.

1 基础知识

1.1 SpMV 概述

SpMV 的计算过程可以表示为等式Ax=y，其中A为参加运算的稀疏矩阵，x为参加运算的稠密向量，y为计算结果向量.在迭代计算中，A为方阵，每次迭代的x向量为上一次迭代中生成的y向量.在实际应用中，矩阵A通常呈现出极高的稀疏性，为了避免存储大量冗余的零元素，矩阵A通常采用稀疏压缩格式进行存储.常用的稀疏矩阵压缩格式包括COO（coordinate list）,ELLPACK[16],CSR（column sparse row）,CSX[17],BRC[18]等.其中，CSR 格式是目前在科学计算领域使用最为广泛的压缩格式，本文基于这一格式进行研究和设计.

图1 中给出基于CSR 格式的稀疏矩阵存储案例以及对应的SpMV 方法.可以看到，CSR 格式保存3个数组结构，分别为：nnz用于保存所有非零元素值，colidx用于保存左右非零元素的列坐标，rowptr用于记录矩阵中每行非零元素的起始位置.在SpMV 的计算过程中，程序按照rowptr数组的索引，遍历nnz数组中存储的矩阵中每行非零元素值，并且与colidx索引的对应x向量元素进行乘累加操作，最终生成y向量的元素.对于x向量访问遵循x[colidx[i]]的间接索引模式.由于稀疏矩阵A的非零元素通常随机分布，所以x的访存地址也是完全随机的.

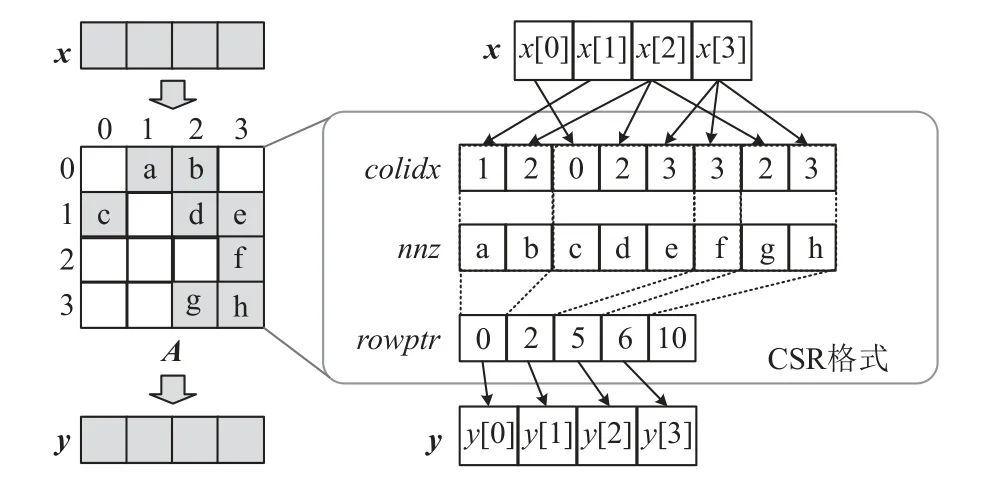
Fig.1 SpMV algorithm using CSR format图1 基于CSR 格式的SpMV 算法

1.2 SpMV 相关工作

由于稀疏矩阵非零元素分布的不规则性，如何在SIMD 架构的现代处理器上高效运行SpMV 一直是研究热点.Liu 等人[7]基于ELLPACK 格式提出名为ESB 的编码格式，通过列分块改善访存的空间局部性，提升SIMD 执行效率.为了充分利用SIMD 单元，CSR5[8]和CVR[9]算法用矩阵多行的非零元素填充SIMD 单元，提升SIMD 单元执行效率，但CSR5和CVR 需要额外复杂的预处理和后处理器操作，CSR5 需要加法树设计与部分和存储，CVR 需要在每次向量计算后动态处理向量单元不同元素的输出，这些额外的数据结构和复杂的计算模式不利于计算效率的提升，因此如何设计低复杂度且高计算效率的SpMV 成为主要的研究挑战.

1.3 SpMV 的性能分析

为了进一步分析SpMV 在现代处理器中的计算行为和性能瓶颈，图2 列出一个典型SpMV 算法的标量代码实现以及在ARMv8 GCC 编译器下生成的对应的指令流示例，并且标出其中的访存指令、计算指令和跳转指令.在图3 中，我们使用Intel VTune Profiler工具测试多个不同领域和尺寸稀疏矩阵的SpMV 性能，并且记录其在Intel Xeon Gold 6146 处理器上的性能分解.从图3（a）中可以看到，访存开销和分支开销构成主要性能瓶颈.本节将逐一分析SpMV 在访存、分支和计算效率上的性能问题.

Fig.2 Pseudo code of SpMV and instruction flow in ARMv8图2 SpMV 伪代码与ARMv8 指令流

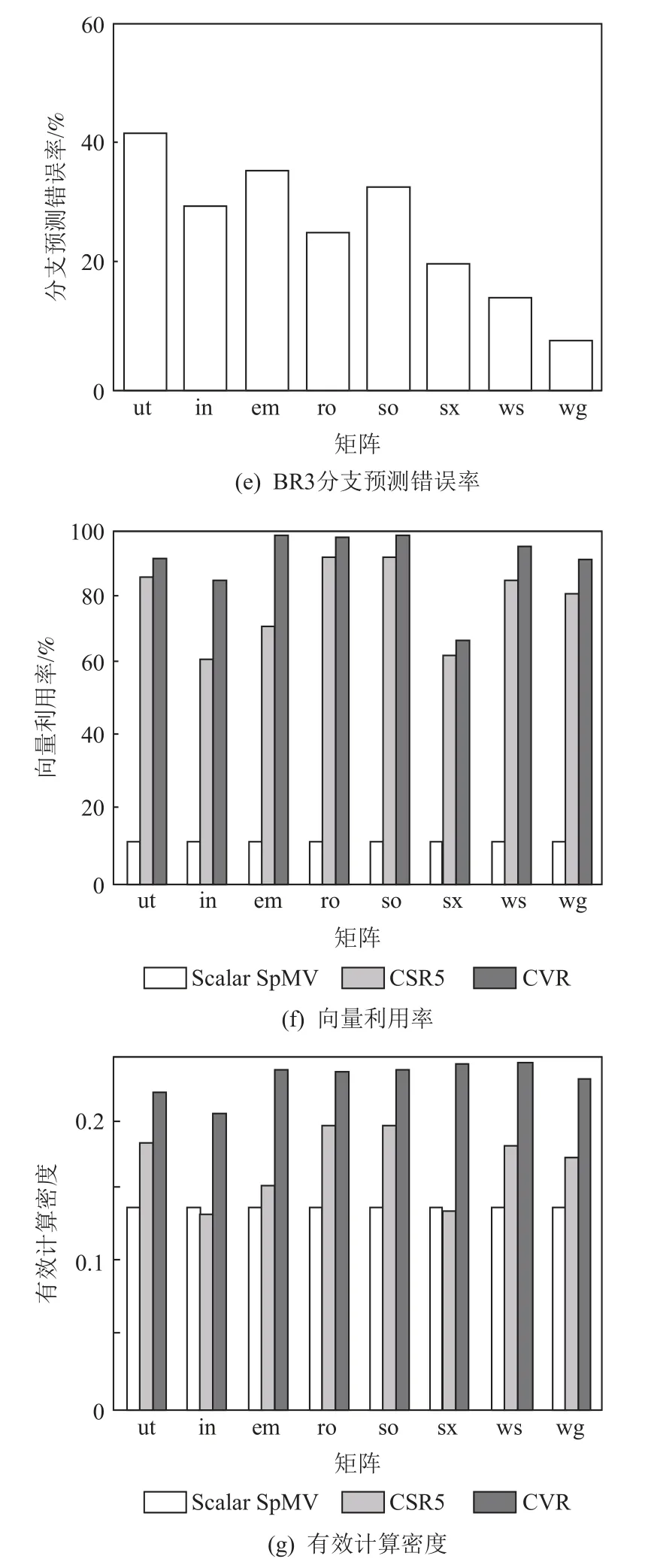
Fig.3 Performance bottleneck analysis of SpMV on Intel Xeon CPU图3 Intel Xeon CPU 上SpMV 的性能瓶颈分析

首先，现代处理器依赖数据局部性来提升缓存效率和降低访存延迟，并且通过数据预取技术来进一步隐藏访存开销.通常现代高性能商业处理器会在缓存配置硬件数据预取器，例如常见的邻行预取器（next-line prefetcher）和步长预取器（stride prefetcher）[19].这些预取器可以动态检测流式访问和定步长访问等简单的访存规律并进行数据预取.

从图2 中可知，SpMV 中对于矩阵数据（rowptr,colidx,nnz）和向量y的访问均是顺序串行的，因此可以高效地被步长预取器识别并预取.相反地，对于向量x的访问呈现出随机的间接索引模式，通常无法被有效地识别和预取[20].此外，由于向量x访问地址的随机性，数据局部性极差，导致缓存使用效率大幅度下降，缓存缺失频繁发生，以上问题均导致访存成为SpMV 的主要性能瓶颈.图3（b）和图3（c）中分别列出了SpMV 的预取覆盖率和访存带宽利用率.可以看到，由于对于x的访问造成大量缓存缺失且无法被有效预取，导致整个计算过程中仅有少量数据访问（不足30%）可以被有效预取.这也导致整体的访存带宽利用率低下，进一步加剧访存性能瓶颈.

其次，现代处理器通常使用分支预测技术来提升流水线的执行效率.硬件分支预测器通过动态记录和分析不同分支跳转指令的历史行为，学习其跳转规律以进行预测.对于具有较深流水线的高性能处理器，分支预测失败需要清空错误指令并且回退处理器状态，这将严重降低处理器的性能.有研究表明，Intel 架构的每次分支预测错误将导致10～15 个周期的CPU 停滞[21].通常认为，分支预测错误率如果超过5%就会明显制约处理器性能.由图2 可以看出，SpMV 的指令流中存在3 个分支跳转指令，分别用于判断末尾行（BR1）、空行（BR2）和行遍历结束（BR3）.其中，BR1 和BR2 具有规律性，可以比较准确地进行预测.然而，BR3 的跳转条件取决于每行的非零元素个数，考虑到稀疏矩阵的随机分布，BR3 行为毫无规律，因此难以被正确预测.因此，BR3 是SpMV 的关键分支跳转.图3（d）列出了不同矩阵中BR3 分支预测情况，可以看到BR3 具有很高的失败概率（20%～40%），这也导致了分支预测成为了SpMV 计算中的关键性能瓶颈之一.

此外，基于现代处理器的SpMV 优化技术通常会采用SIMD 技术来提升计算并行度，从而优化计算性能.SIMD 支持每条指令实现最多VL个元素的并行运算.然而，由于稀疏矩阵的高度稀疏性和不规则性，SpMV 运算中通常难以实现VL个元素的充分并行，因此需要通过增加遮蔽向量（mask vector）的方式降低其并行度.为了衡量SIMD SpMV 算法的运算效率，我们定义有效计算密度（effective computation density）指标D和浮点计算性能（floating point computing performance）指标FPCP，其公式为：

其中，VInsnNum表示SpMV 中参与有效计算的SIMD指令；VRate表示向量利用率，即未被屏蔽的SIMD 向量元素的平均占比；TotalInsnNum表示程序执行的指令总数；IPC表示单位周期数执行指令数；Frequency表示处理器的执行频率.对于给定的工作负载，IPC相对稳定，仅在较小范围内波动，因此由式（2）可知，计算密度D与计算性能FPCP呈近似正相关关系.需要注意的是，这里的有效计算指的是对于每个非零元素的乘加运算，因此其数量是由矩阵的非零元素个数决定的.通常基于SIMD 的研究主要关注向量利用率VRate这一指标，然而通过式（1）可知，有效向量计算指令在整体指令流中的密度也非常重要.在一些算法中，为了追求高利用率而提升程序的复杂度反而妨碍了整体计算密度的提升.此外，分支预测错误会造成大量无效指令被流水线发射，从而导致整体计算密度的下降.

图3（e）比较了Scalar SpMV 算法和2 种SIMD 优化算法CSR5[8]和CVR[9].可以看到，通过优化，CSR5和CVR 均达到了很高的向量利用率，且远超于Scalar SpMV 算法.然而，通过图3（f）的计算密度指标对比可以看到，CSR5 和CVR 的整体计算效率仅稍好于Scalar SpMV.这是由于CSR5 和CVR 算法为了提升向量利用率，引入了额外的程序复杂度，从而导致整体指令数的上升，削减了向量指令的密度，由式（2）可知，计算指令密度下降会导致计算性能下降，不利于SpMV 的性能优化.这一实验结果说明，为了有效提升计算性能，不应该仅关注向量利用率，而是应综合考虑向量利用率与程序复杂度的权衡，尽可能降低与核心计算任务无关的指令数量.

通过对于SpMV 访存、分支跳转和计算并行度的分析，明确了核心性能瓶颈和指标.本文基于这些分析结果提出了pvSpMV 方法，通过构建访存和分支跳转高度可预测的计算方法，结合低复杂度的向量化计算，实现了SpMV 计算方法的全面优化.

2 访存优化方法

2.1 步长预取器工作原理

步长预取器是现代商业处理器中最常见的硬件预取器，它通过监控处理器发送给缓存的访存指令多个内存地址，识别连续步长访问模式的访存序列.建立步长访存模式后，步长预取器的预取地址生成模块（address generator）监听处理器发送给缓存访存请求，根据访问地址计算预取数据的内存地址，计算公式为：

其中，load addr为触发预取器生成预取请求的访存地址；prefetch depth为预取深度，指一个访问向量x的地址产生预取请求的数量，为硬件预取器参数；stride为访存步长，指连续访问地址之间的差.预取器产生预取请求并通过预取队列（prefetch queue）发送给下一级访存结构，在程序需要这个请求数据时，数据已经被放入缓存，达到隐藏访存延迟的效果.

在SpMV 运算过程中，对向量x的访存地址由于非零元分布不规则且不连续，因此步长预取器不能有效预取向量x.而传统的SpMV 优化策略一般通过分块的方式，使得单块的数据尺寸小于缓存尺寸，改善访存的空间局部性，忽视对向量非规则访问模式的分析和优化.本文从硬件步长预取器的角度分析SpMV 运行过程中的访存效率问题，通过将非规则的向量访问模式序列化，使得步长预取器能有效预取向量，隐藏访存延迟，优化访存性能.

2.2 向量访存序列顺序化

图4 以4×8 矩阵为例，描述SpMV 运算对向量x不同元素的访问过程.B→C→H→A→D→G 是矩阵第1 次访问向量元素的序列顺序，由于缓存未加载向量元素，第1 次向量元素的访问会产生缓存未命中，并从内存获取数据.假设后续对同一元素的访问由于时间局部性会在缓存命中，则访问向量元素对应的缓存未命中序列（cache miss sequence）为B→C→H→A→D→G，是顺序访问模式，能够利用步长预取器进行数据预取.因此以对向量不同元素的第1 次访问的先后访问顺序对向量x进行重排，缓存预取器的预取模式识别模块（pattern detector）通过观测向量x对应的缓存未命中序列，识别向量x的连续访存模式.

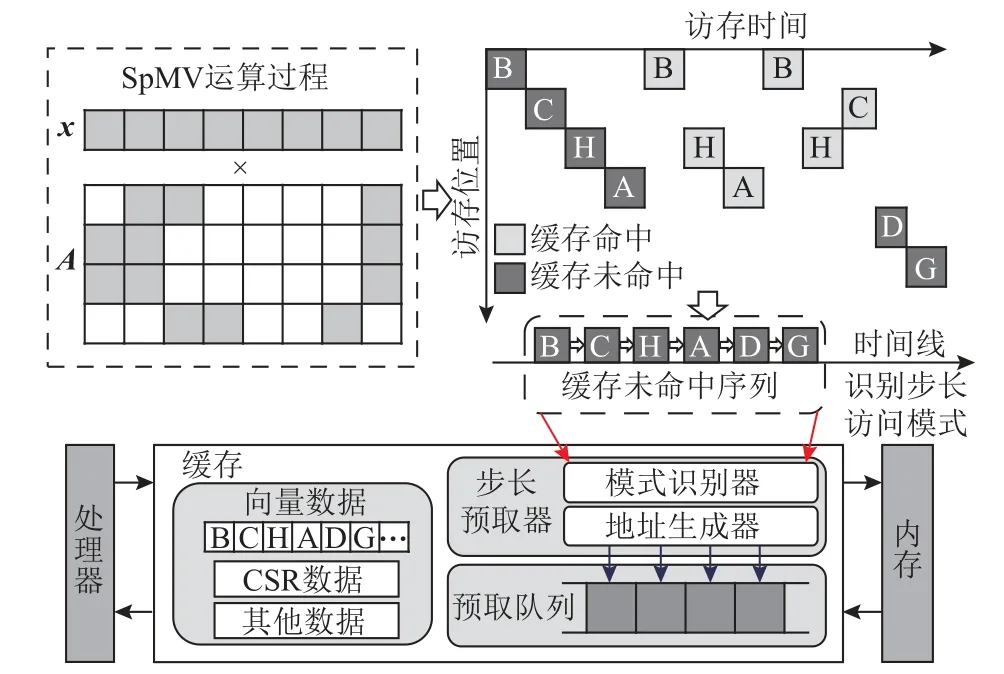
Fig.4 Illustration of SpMV memory access pattern图4 SpMV 访存模式示意图

2.3 矩阵分块策略

访存优化方法关键在于步长预取器能识别访问向量x对应的缓存未命中这一顺序序列.若重排后的向量x尺寸过大，导致部分已被访问的向量元素被缓存替换，就会影响缓存对向量元素访问模式的识别.因此要求后续对相同元素的访存尽可能在缓存命中，步长预取器观测对向量元素的第1 次访问产生的缓存未命中请求，构建连续顺序的访问序列.

解决方案是从行方向对稀疏矩阵切块，在块内分别做SpMV 运算.切块思路是让单个矩阵块内对向量x元素的第1 次访问被缓存的步长预取器观测，而其余次访问在缓存命中，并且预留足够的缓存空间给SpMV 运算要用的CSR 数据结构（value,rowptr,colidx），如图4 所示.通过实验分析性能结果，将单个矩阵块的重排后的向量x′尺寸设置为0.5 倍缓存尺寸.

2.4 基于Bitmap 的行重排策略

SpMV 在科学计算和图计算中需要多次迭代，上一轮迭代的计算结果作为下一轮迭代的数据输入.由于每次迭代都需要用本次计算的输出向量y更新下一次运算要使用的重排后的向量x′，因此如何减少更新向量x′的访存开销对性能优化十分重要.

本文采用基于Bitmap 的行重排策略缓解向量x更新开销过大问题，如图5 所示.将稀疏矩阵的每一行分为不同的区域，将含有最多非零元素个数的区域对应的Bitmap 位标注为1，其余位标注为0，得到矩阵每行对应的Bitmap 值.并利用Bitmap 值以从大到小的顺序对矩阵行进行重排，目的是让矩阵的非零元素分布更规律，近似为对角线分布，这样不同块的重排后的向量x′尺寸更小，向量x′的更新开销减少.

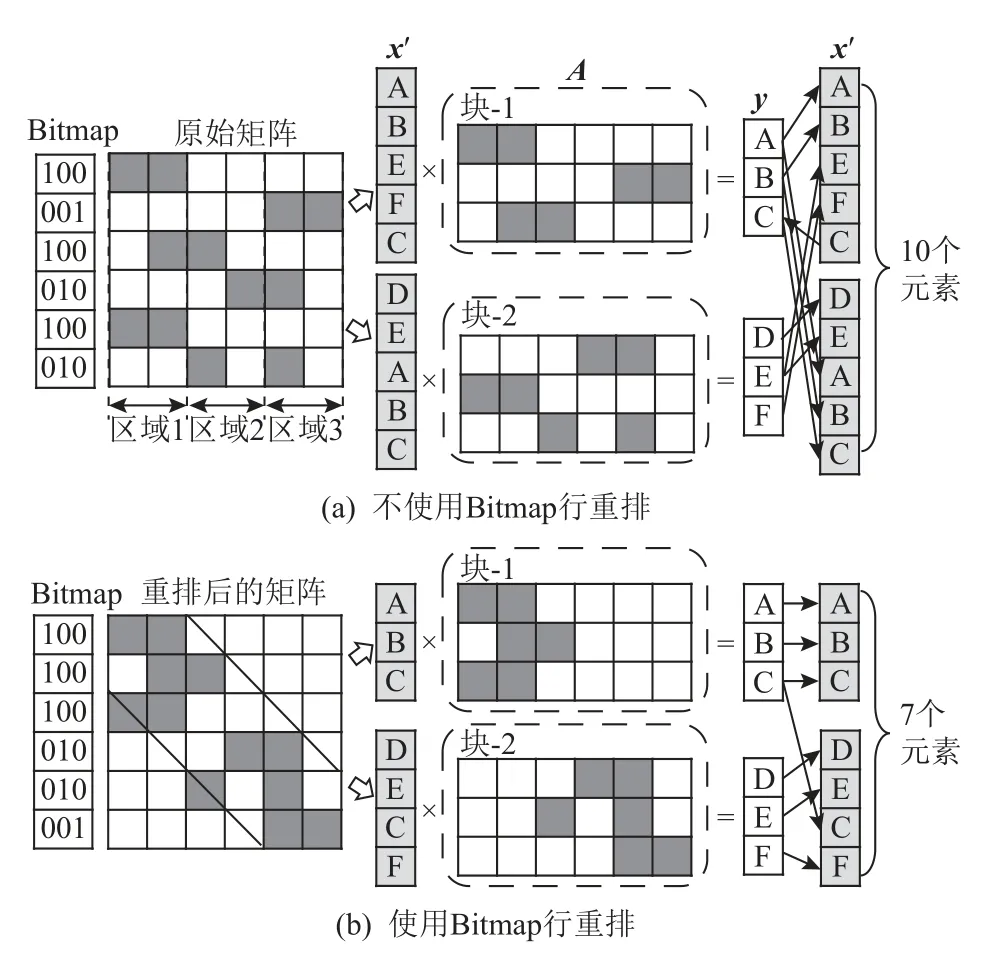
Fig.5 Illustration of Bitmap row reorder strategy图5 Bitmap 行重排策略示意图

2.5 访存优化方法介绍

访存优化方法如图6 所示.

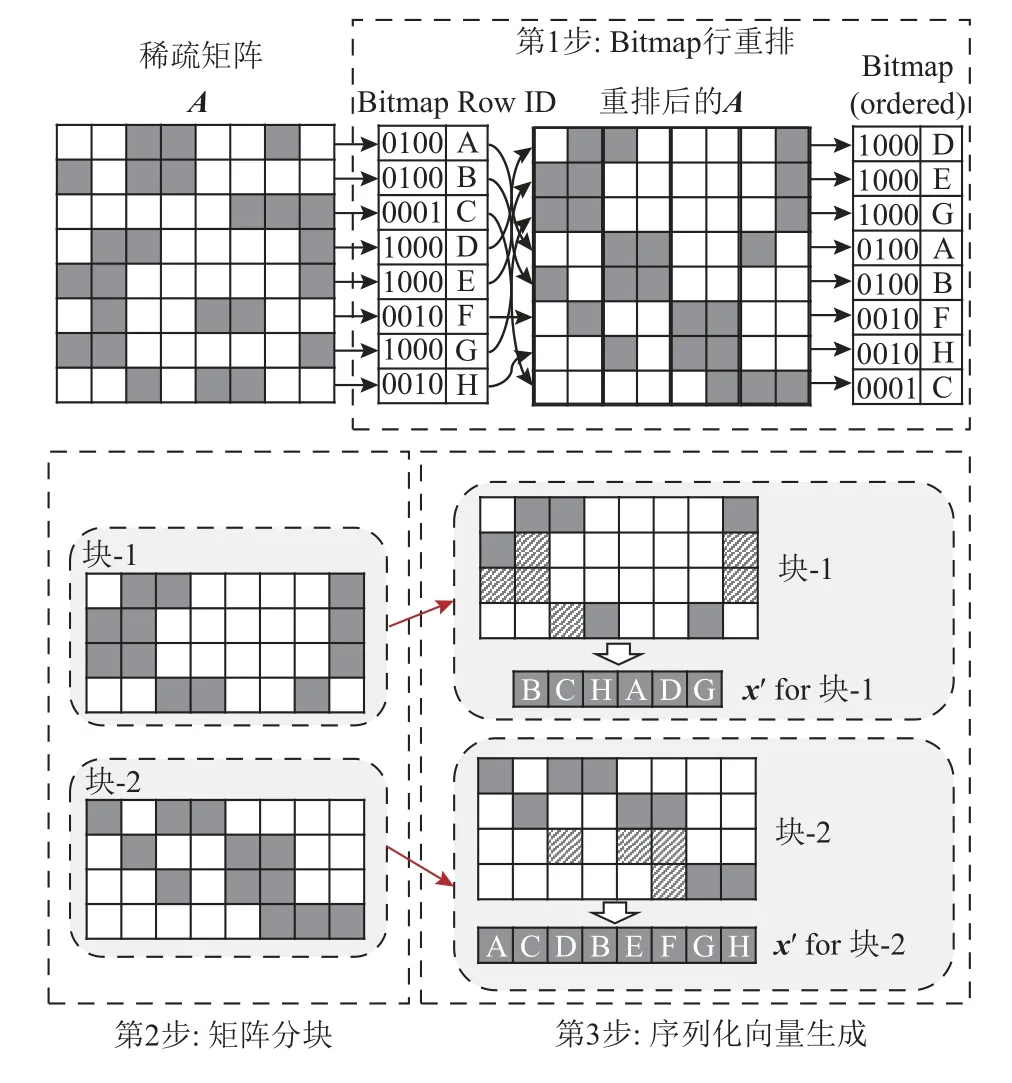
Fig.6 Illustration of memory access optimization method图6 访存优化方法示意图

图6 所示的主要步骤包括：

1）基于Bitmap 的行重排（Bitmap row reordering）.让矩阵的非零元素呈近似对角线分布.

2）矩阵分块（block partitioning）.从行方向将矩阵切分为不同矩阵块，每个块的非零元素存储为0.5 倍二级缓存尺寸.

3）序列化向量生成（serial vector generation）.根据矩阵块对向量x各分量的索引前后顺序，构建该矩阵块对应的重排后的向量x′.

本访存优化方法的研究思路是设计预处理算法，将向量x的不规则访问模式转化为对向量x′的顺序访问模式，借助处理器缓存的硬件步长预取器实现对重排后向量x′访问模式的识别，准确预测程序要使用的向量x′数据的内存地址并做数据预取，达到优化SpMV 访存瓶颈的效果.

3 分支预测优化方法

如第2 节所述，分支预测误判开销是影响SpMV性能的重要来源之一，但现有研究尚未对SpMV 运行过程中分支跳转行为进行细粒度分析和优化，本文考虑稀疏矩阵的分支跳转特征，提出行重排策略优化SpMV 的分支预测开销.

通过图2 中的SpMV 指令流分析可知，对于稀疏矩阵每行非零元素的循环遍历构成了SpMV 的关键分支跳转.由于每行非零元素个数均不相同，这一分支跳转的行为往往难以被正确预测.图7（a）中展示了典型稀疏矩阵web-Stanford的非零元素分布特征.可以看到，行长度的分布呈现出幂律特征，即绝大部分的矩阵行的非零元素个数很少，仅有少量的行中非零元素数量较多.这一特征被称为Scale-Free，它是在图结构中广泛存在的分布特征[22].图7（a）中展示了基于BHR（branch history register）和PHT（pattern history table）技术的分支预测情况示例.可以看到，在行长度随机分布的情况下，现有分支预测技术难以进行准确预测，并且倾向于在每行循环遍历的开始和最后迭代时产生预测错误.我们还可以看到，在长行的循环遍历中，分支预测错误的比例相对较低.然而，由于大部分基于图结构的稀疏矩阵符合Scale-Free 幂律分布特征，大部分行的非零元素数量都很少，因此导致较高的分支预测错误概率.

为了解决这一问题，我们采用矩阵行重排的方法.如图7（b）所示，通过按照行长度进行排序，使得非零元素个数相同的行构成一组（group），并且在内存中相邻排列，保证连续若干行的分支跳转模式相同，从而提升分支预测的准确率.这一方法可以广泛适用于基于局部跳转历史的分支预测技术，对于传统的BHR/PHT 分支预测器和更为先进的TAGE 分支预测器[23]都可以达到很好的预测效果.此外，行重排的过程打乱了原有的矩阵分布，因此可能会破坏某些稀疏矩阵的原有结构特征，从而造成计算效率的下降.为了抑制这一现象，我们将矩阵中连续的2 048行划分为一个簇（bundle），并且仅在簇内开展行重排，从而限制了乱序范围.实验结果表明，采用2 048 的排序范围已经可以实现很好的分支预测优化效果和接近100%的分支预测正确率.

4 SIMD 计算优化方法

已有方案虽然能实现较高的SIMD 单元利用率，但是会引入额外的指令复杂度，不利于SpMV 计算性能的优化.本文借鉴已有研究思路，提出简洁高效的SIMD 并行计算策略，提升SpMV 的计算性能.

为了进一步提升SpMV 的计算性能，pvSpMV 采用SIMD 指令集实现了高效的并行计算.由式（1）可知，SIMD 计算效率优化的关键在于提升有效计算密度，即提升非零元素乘加运算在整个执行指令流中的密度.为达成这一优化目标，需要提升SIMD 向量利用率，并且降低总体的指令发射数量.通过分支预测优化技术，pvSpMV 已经大幅度减少由于分支预测错误而产生的错误指令发射.在本节中，我们通过构建简洁的计算核心进一步降低程序复杂度，从而在保持高利用率基础上减少与有效计算无关的指令数量.

具体来说，分支预测优化后的矩阵格式呈现多簇的结构，每簇中包含有多组，每组中包含有多个长度相同的行.图8 给出了一个簇内部的结构示例.假设SIMD 的向量长度为VL，则可以在每个组中收集VL整数倍的行作为一个段（segment），并且将段中的多个行按照VL的长度进行转置存储.每组中剩余的行统一存储为碎片集合（fragment）.最终，一个簇会被转化为若干个段和一个碎片集合.

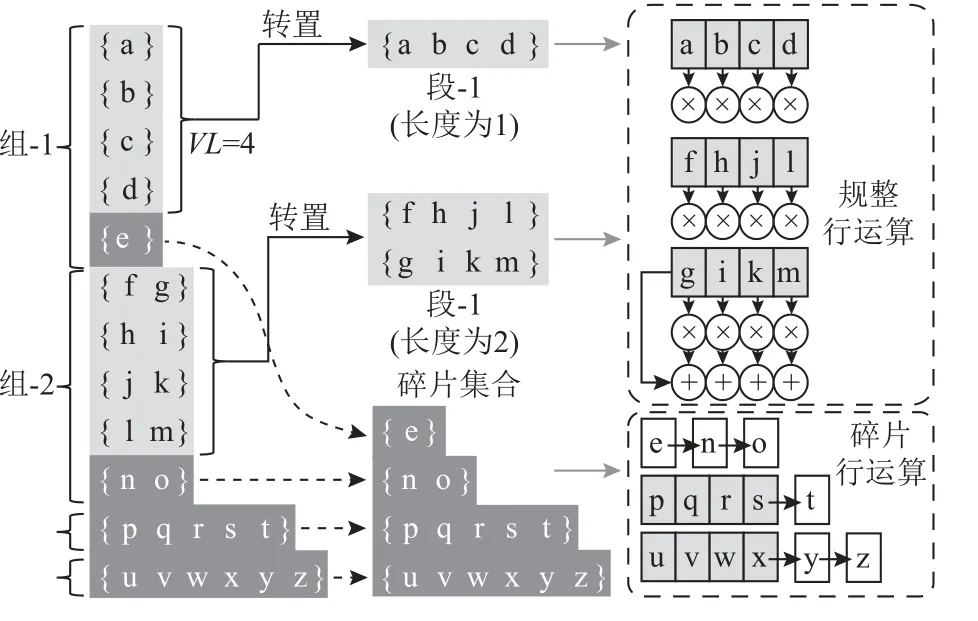
Fig.8 Optimization of SIMD computation using two simple computing kernels图8 基于2 种简化运算核心的SIMD 计算优化（VL=4）

基于这种存储格式，pvSpMV 设计了2 类计算核心，分别用于对段和碎片集合进行计算.如图8 所示，对于段的计算采用简单的SIMD 乘累加方式，并行开展VL个行的计算.由于段的长度被规定为VL的整数倍，因此可以充分使用SIMD 向量长度而无需使用遮蔽向量.对于碎片集合，采用逐行的方式进行计算.在每行的计算中，首先使用SIMD 指令计算VL整数倍的非零元素，然后使用标量指令计算剩余非零元素.这样就确保了每个SIMD 指令都可以充分利用向量资源，且无需使用遮蔽向量，降低了代码的复杂度.而且，由于标量计算的元素数量很少（每行的标量计算元素数量不超过VL-1），因此标量计算并不会对整体性能构成影响.实验结果表明，在大多数稀疏矩阵中，使用标量计算方法可以实现绝大多数元素的全向量长度的SIMD 并行计算，仅有不足3%的元素需要使用标量指令计算，因此充分发挥了SIMD 架构的计算并行度.更重要的是，这种计算核心的构造非常简单，代码复杂度很低.采用这一优化方法，可以大幅度提升有效计算密度，充分发挥SIMD 架构的计算能力.

5 pvSpMV 整体框架与实现

5.1 整体框架

基于第2～4 节所述的面向访存、分支预测和并行计算效率的优化方法，我们提出pvSpMV 方法，通过构建一种新型的稀疏矩阵存储格式和SpMV 计算方法，实现计算性能的全面提升.

由于很多应用场景中需要多次迭代计算SpMV来进行问题求解，因此稀疏矩阵预处理的开销可以被有效地分摊到多次迭代过程中，其对整体性能的影响可以忽略.pvSpMV 结合了上述多种优化技术，通过一系列预处理方法进行基于CSR 格式的稀疏矩阵存储方法优化，提升其在计算过程中的访存和分支预测的可预测性.图9 给出了pvSpMV 对于稀疏矩阵预处理的流程图，具体划分为6 个步骤.

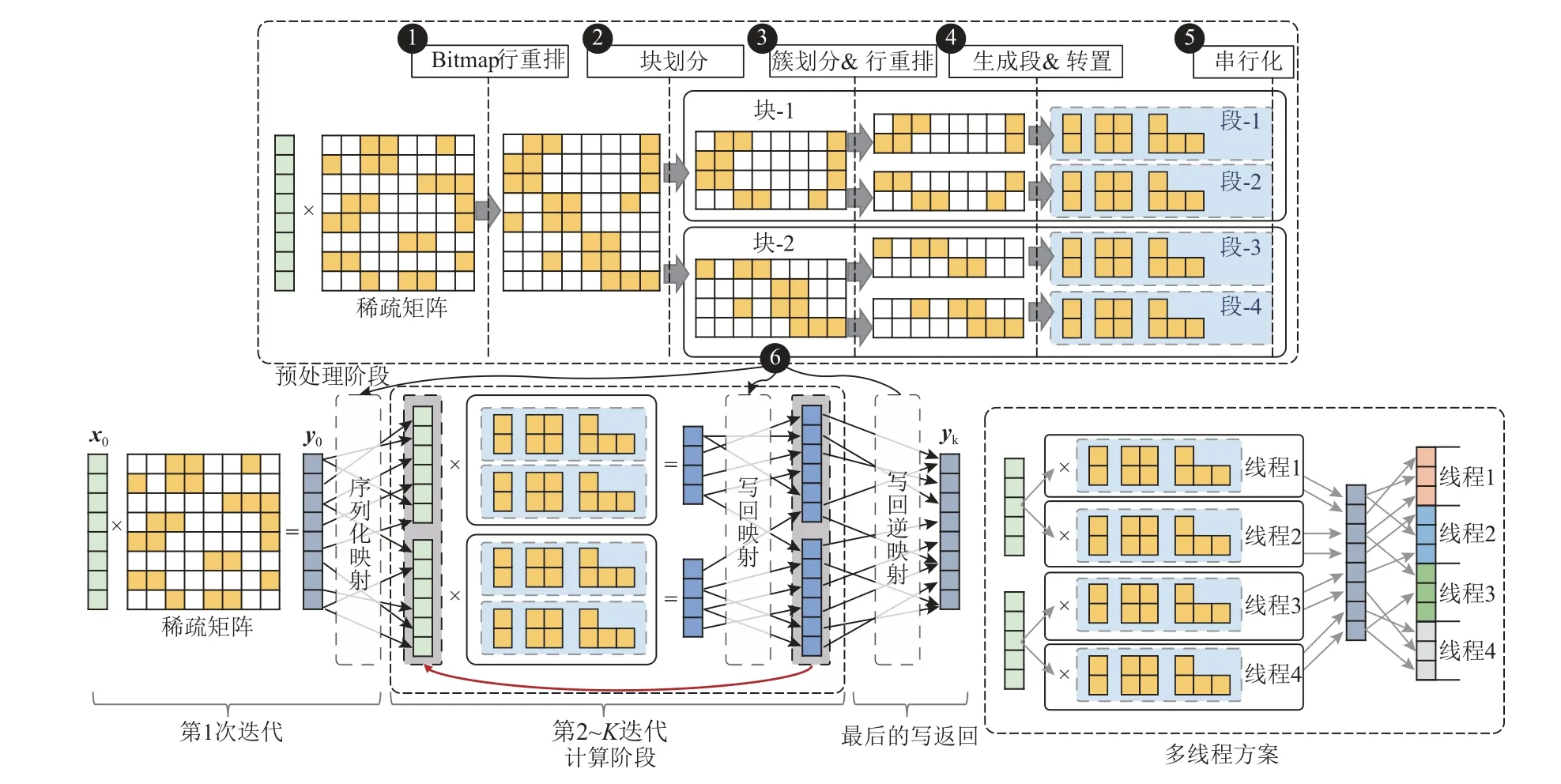
Fig.9 Block diagram of preprocessing flow,computation method and multi-thread implementation of pvSpMV图9 pvSpMV 的预处理流程、计算方法和多线程实现框图

1）比特图优化.对于原始CSR 格式稀疏矩阵，采用基于比特图的行重排方法进行矩阵变换，提升相邻行的非零元素分布特征，记录行重排映射关系R1.

2）块划分.首先根据缓存尺寸确定每块（block）子矩阵的向量长度；然后对比特图优化后的矩阵进行分块，每块子矩阵包含若干个连续的矩阵行，并且每块子矩阵所索引的向量元素可以在缓存中全部存储.

3）簇划分.在每块子矩阵内部进行簇划分，每个簇包含2 048 个相邻的行.在簇的内部，对2 048 个行进行重排分组，每组的各个行具有相同的非零元素数量，记录行重排映射关系R2.

4）生成段和碎片集合.在每个簇的内部，按照SIMD 向量长度VL，在每组中收集数量为VL整数倍的行，并且转置存储为段；剩余的行组成碎片集合；记录行重排映射关系R3.

5）串行化.对于每块子矩阵，按照其中各个簇的计算和访存模式，记录输入向量的串行化映射关系S1，并且修改子矩阵数据结构中对应位置colidx的值.

6）生成写回顺序.为了支持迭代的SpMV 运算，每次迭代后的计算结果需要被重组为下次迭代所需的输入向量顺序，pvSpMV 记录了每行的计算结果与下次迭代输入向量中对应位置的映射关系，记录为W1[i]=S1[R3[R2[R1[i]]]]；并且还需要在最后一次迭代后，将运算结果还原为原始向量顺序，因此还需要还原的映射关系，记录为W2=Rev（R3[R2[R1[i]]]），其中Rev（）表示将映射关系的键和值进行对调的函数.

综上所述，经过pvSpMV 预处理后的稀疏矩阵可表示为若干块包含一系列簇的子矩阵组合，且每个簇的行均按照SIMD 计算模式进行重组.此外，还会存储3 个映射关系，分别为S1，W1和W2.

5.2 计算方法

根据5.1 节所述的稀疏矩阵格式，图9 给出了基于pvSpMV 的多次SpMV 迭代计算流程.这一流程包含5 个步骤：

1）在第一次迭代中，输入向量x0与原始的CSR格式稀疏矩阵进行SpMV 运算并生成结果向量y0；对于y0，使用S1映射对其进行变换，将其转换为符合串行访问方式的元素顺序.

2）使用转换后的向量与各块子矩阵进行SpMV运算，运算结果写入稠密排列的结果向量中.在这一过程中，每块矩阵均构成了对于向量元素的串行访问，因此可以有效触发数据预取，并且提升了缓存的局部性.

3）在各块子矩阵均运算结束后，对于运算生成的结果向量按照W1进行重排，使其符合串行化访存优化的向量元素顺序，并且将转换后的结果向量作为运算向量，与优化后的稀疏矩阵格式开始下次迭代.

4）重复步骤2 和步骤3，直到算法收敛.

5）在最后一次SpMV 计算迭代结束后，使用W2对结果向量进行变换，使其元素顺序恢复为原始的向量顺序，至此多次迭代的SpMV 完成.

在这5 个步骤中，核心操作为步骤2 和步骤3，它们会经历多次迭代，是决定算法性能的关键计算步骤.其中，步骤2 的向量访存模式在优化后呈现出串行访问特征，可以有效借助数据预取器实现高效地取数，此外，由于分支预测优化和向量并行计算优化，步骤2 的计算行为呈现出高度可预测性和极低的程序复杂度特征，可以充分发挥现代高性能处理器的计算能力，构成了pvSpMV 的主要性能收益来源.与之相对应的，步骤3 需要对下一次迭代所需的向量进行赋值，这一过程需要对步骤2 生成的结果数据进行乱序读取，因此会带来额外的性能开销.因此，步骤2 的收益与步骤3 的开销之间的权衡是很关键的.具体来说，步骤3 的开销正比于迭代向量的大小，因此与稀疏矩阵的分块数量直接相关.本文经过理论分析和实际测试，发现按照50%二级缓存的容量设置每块的向量元素数量是较为合理的.这一尺寸设计不仅可以满足访存优化方法所需的缓存尺寸限制，而且可以避免过多分块所导致的步骤3 开销过大问题.实验表明，pvSpMV 算法中，对于步骤2 的访存优化所带来的收益往往会超过步骤3 乱序写回所导致的额外开销，因此整体预期具有良好的性能优化效果.

5.3 多线程计算方法

pvSpMV 具有较好的多核可扩展性，可以通过在多线程中动态分配块和簇的方法，实现便捷的多线程计算扩展.图9 详细展示了pvSpMV 的多线程计算方法.具体来说，在步骤2 中，可以根据矩阵大小和线程数量选择不同的调度策略.为了确保多线程之间的动态负载均衡，pvSpMV 在块数达到线程数2 倍以上的情况下，会选择以块为粒度进行多核的动态调度；当块数较少时，pvSpMV 会采用以簇为粒度的方式进行多核计算调度，从而保证多核的动态负载均衡策略不会失效.在步骤3 中，pvSpMV将需要赋值的下次迭代所需向量按照1 024 个元素为粒度进行了划分，每个线程抢占式地进行不同组1 024 个元素的赋值操作，并且在赋值过程中读取共享的结果向量数据.这样的处理方法既可以确保线程间的负载均衡，又可以避免由于写冲突所导致的“伪共享”（false sharing）问题.

6 性能评估与讨论

6.1 实验设置

我们在商用x86 平台评估设计的性能表现，表1描述了实验平台微架构参数，实验平台为Intel Xeon Gold 6164 服务器，处理器架构为Intel Skylake-X 多核架构，包含一级数据缓存和二级缓存为各个处理器核心私有，容量分别为32 KB 和1 MB，三级缓存为多个处理器核心共享，三级缓存容量为24.75 MB.为了避免Intel 处理器在高频工作下触发DVFS 的自动降频技术，本文将处理器频率固定为2.5 GHz，从而提升测试环境的稳定性.另外，我们还在AMD 平台测试方案的性能.

Table 1 Evaluation Platform Parameters表1 实验平台微架构参数

用于研究SpMV 性能的基准方案选择Intel Math Kernel Library[6]（MKL 版本为2020.2）中提供的SpMV计算核心实现，采用无优化性能作为基准.pvSpMV代码采用GCC 编译器（GCC 11.3）进行编译，并且采用了Intel AVX-512 向量指令集.此外，本文还对比了其他先进SpMV 技术的性能，包括CSR5[8]，CVR[9]，CSR2[24]，以及经过优化流程后的MKL SpMV 方法.

本文的测试数据选自公开测试集Suitesparse Matrix Collection[15]，并选取了其中与图计算和科学计算相关的SNAP,Kamvar,Pajek,DIMACS10,Belcastro数据集.本文的全部测试矩阵集合包含84 个稀疏矩阵，覆盖了社交网络、路径规划、电网分析等多个应用场景.

6.2 关键指标评估

为了分析pvSpMV 对于分支预测和并行计算效率等性能瓶颈的优化效果，我们在本节中对pvSpMV的关键性能指标进行评估.为了测试各项指标，在所有测试集中挑选了不同类型、不同尺寸的24 个矩阵，并且分别测试对比了每个矩阵在MKL[6],pvSpMV,CSR5[8],CVR[9]这4 种优化方法上的指标结果.

我们首先评估了分支预测优化的效果，实验结果如图10 所示.可以看出，MKL 和CSR5 均有较多的分支预测错误率，CVR 由于计算模式相对简单，分支预测的难度更低.而pvSpMV则实现了分支预测的完全优化，基本消除了分支预测错误开销.

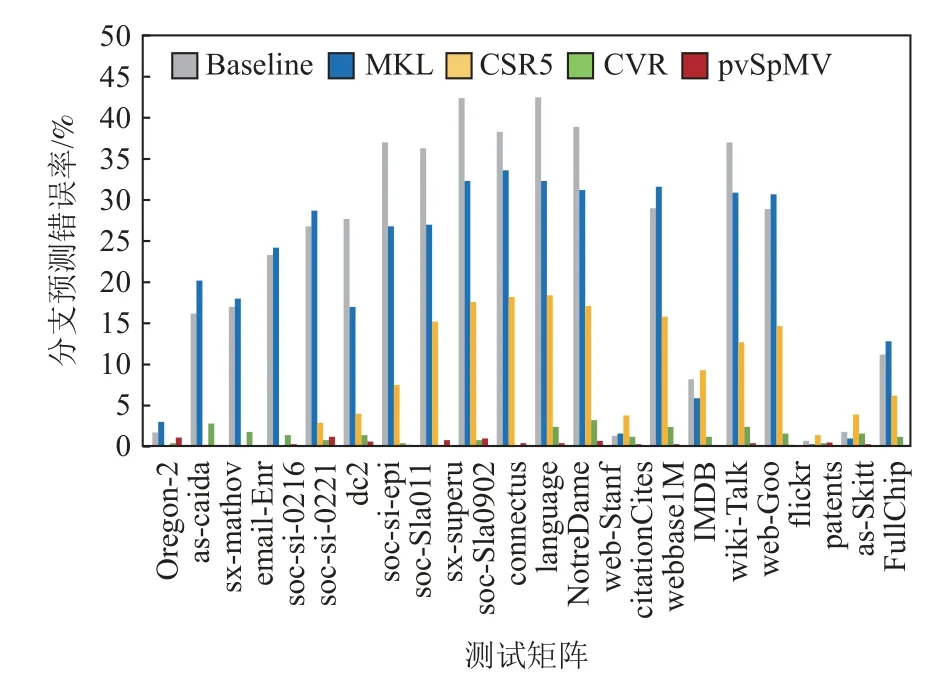
Fig.10 Optimization evaluation of branch prediction图10 分支预测优化评估

之后，我们评估了SIMD 并行计算的优化效果，具体分为2 项指标，分别是：SIMD 指令的向量利用率，实验结果见图11（a）；SIMD 指令的有效计算密度，实验结果见图11（b）.通过这2 项指标的对比可以看到，CSR5 和CVR 算法虽然可以实现较高的向量利用率，但是其整体的有效计算密度提升较为有限，这是由于它们计算程序的复杂度导致了额外指令数.与之相比，pvSpMV 方法不仅可以达到很高的向量利用率，而且通过低复杂度的程序实现，有效抑制了冗余代码的数量，确保SIMD 指令的有效计算密度可以有效提升.

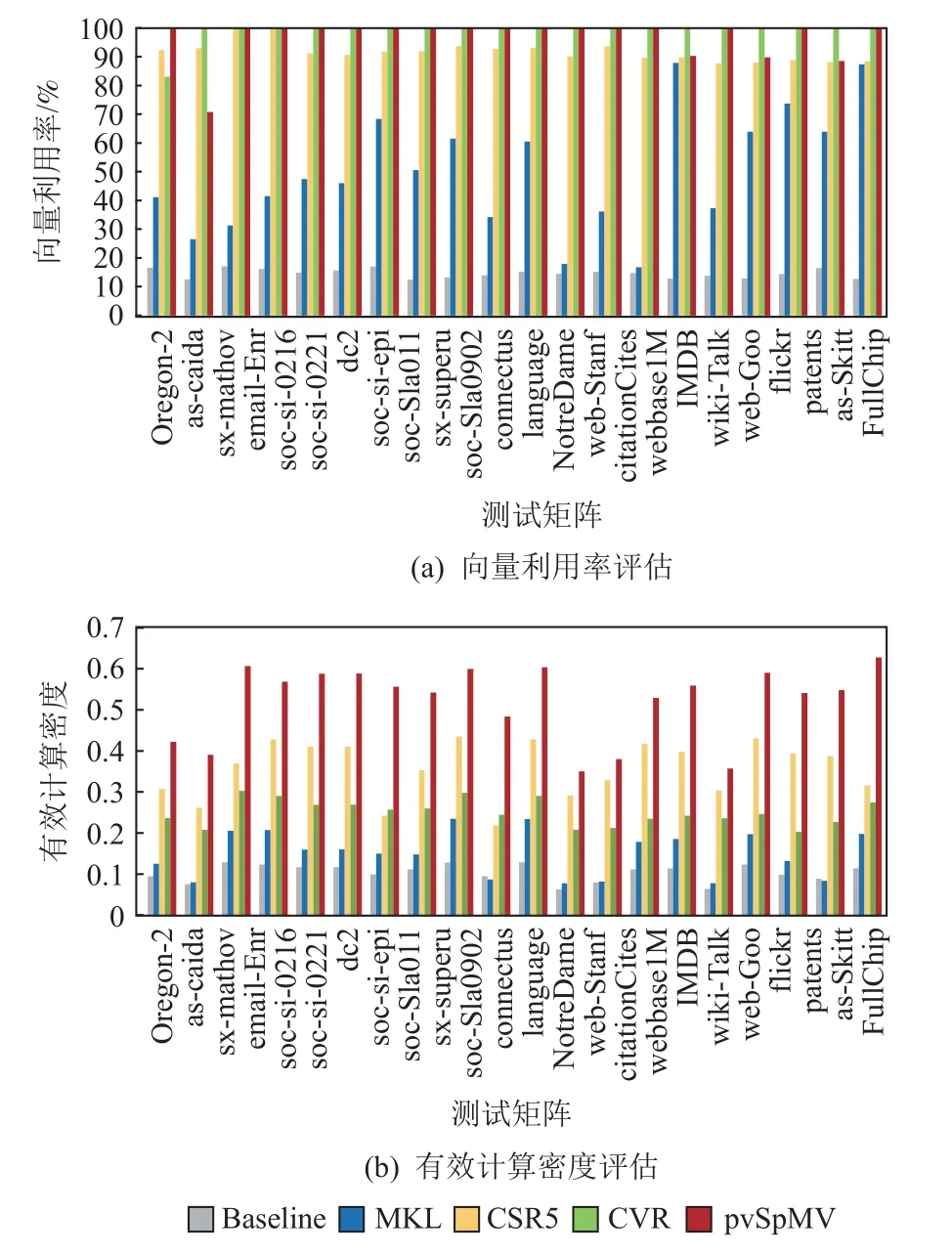
Fig.11 Evaluation of vector usage and computing density图11 向量利用率和有效计算密度评估

最后，我们评估了pvSpMV 对访存效率的优化效果，实验结果如图12 所示.二级缓存缺失数越高，则访存效率越差.可以看到，相较不加优化方法的基准方案，pvSpMV 显著降低二级缓存缺失数，对访存效率有明显提升，这也证明基于Bitmap 的行重排策略和向量x′访问序列化对访存效率的优化效果.

Fig.12 Evaluation of L2 cache miss number图12 二级缓存缺失数评估

6.3 整体性能评估

本节对pvSpMV 的整体性能进行了全面的评估和测试.基准性能为MKL 在不进行优化处理时的性能.图13（a）中给出了pvSpMV 以及其他对比方法在全部85 个稀疏矩阵上的单线程计算性能和相比于基准性能的加速比.可以看到，pvSpMV 在几乎所有测试矩阵中均取得了最高的性能，并且相比于基准方法的收益非常可观.具体来说，pvSpMV 的单线程平均算力达到了1.58 GFLOPS，相比于基准性能的0.64 GFLOPS 取得了2.6 倍的性能提升，并且相比于CSR5 和CVR 分别取得了1.3 和1.58 倍的加速比.同时可以观察到，随着矩阵尺寸的增加，计算性能逐渐下降，这是由于访存瓶颈的逐渐凸显导致的.通过pvSpMV 的优化，可以在大型矩阵的计算中取得超过1.50GFLOPS 的性能，这说明了本文采取的优化方法可以有效缓解访存瓶颈，提升整体计算性能.

Fig.13 Performance comparison between pvSpMV and other comparative methods over 85 sparse matrices图13 pvSpMV 和其他对比方法在85 个稀疏矩阵上的性能对比

我们还评估了多线程的计算性能.图13（b）给出了使用8 线程计算的性能测试结果.为了保证测试的公平性，我们关闭了Intel 处理器的SMT 技术，并且通过计算核心绑定的方式确保所有线程均运行在同一个NUMA 节点上.通过实验结果可以看到，CVR和MKL 的多核可扩展性较好，而pvSpMV 的性能提升则不足8 倍.这一现象的原因有2 点：1）pvSpMV通过提升访存的可预测性来充分发挥数据预取器的取数能力，然而多线程模式下可能会以簇为粒度进行多线程调度，这可能会破坏向量元素的访存串行性，从而降低数据预取的收益；2）由于pvSpMV 大幅提升了计算效率和取数效率，导致在多线程下的访存带宽趋向饱和，因此导致整体性能收益不足8 倍.然而，即使在这种情况下，pvSpMV 仍然取得了最高的多线程性能，并且相比于基线性能实现了平均2.8倍的加速比，相比CSR5 和CVR 分别实现了1.3 倍和1.7 倍的加速比.

我们还在AMD 处理器平台评估计算性能，采用256b 的AVX2 向量指令集，与MKL[6]和CSR2[24]方法比较性能，实验结果如图14 所示.相较基准方案，pvSpMV 实现了1.7 倍的性能加速比，证明pvSpMV能部署在多个不同的处理器平台且能实现显著的性能提升.

Fig.14 Performance comparison between pvSpMV and other comparative methods on AMD platform图14 pvSpMV 和其它对比方法在AMD 处理器平台的性能对比

为了进一步分析多线程的性能问题，我们进而挑选了典型稀疏矩阵coPapersCiteseer（包含32×106个非零元素），并且测试了从线程1 到线程12 不同情况下的性能结果，如图15 所示.可以看到，随着线程数趋近并超过8 线程，pvSpMV，CSR5 和CSR 均出现了性能增长变缓，考虑到pvSpMV 有效地优化了访存效率和CPU 执行效率，这一现象显示出访存带宽可能已经接近饱和状态.

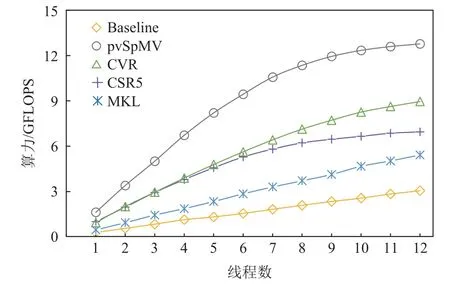
Fig.15 Performance comparison of different number of threads图15 不同线程数的性能对比

6.4 有效性分析

本文通过结合多种优化手段实现了pvSpMV 的全面优化.本节将通过一系列消融实验，逐步探讨不同的优化方法对于整体性能的效果.具体来说，为了分项测试各个优化方案，我们设计了4 个对比实验方案：

1）pvSpMV-base.作为研究pvSpMV 的基线性能方案，这一方案采用最朴素的CSR 计算方法，采用标量指令集，不采用访存优化、分支预测优化或SIMD指令.

2）pvSpMV-v1.基于pvSpMV-base 版本，增加了基于bitmap 和分块的访存优化，增加了矩阵访存模式的串行化处理.

3）pvSpMV-v2.基于pvSpMV-v1 版本，增加了基于分簇和行重排的分支预测优化方法.

4）pvSpMV-v3.基于pvSpMV-v2 版本，增加了基于分段和碎片集合的SIMD 指令优化方法.这一版本是完整的优化版本，也是正式的性能评估版本.

图16 展示了在全部85 个测试矩阵上不同实验方案相比于基准性能（pvSpMV-base）的加速比.可以看出，在采用访存优化技术后，pvSpMV-v1 相比于基准的朴素CSR SpMV 版本已经取得了明显的收益，并且在使用分支预测优化和SIMD 优化技术后均可以获得可观的性能收益.这一实验结果表明，pvSpMV的各项优化方法可以有效缓解相关性能瓶颈，共同完成了计算性能的全面提升.

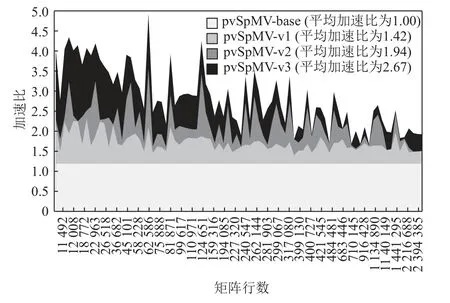
Fig.16 Ablation experiments on pvSpMV optimization methods图16 pvSpMV 各种优化方法的消融实验

6.5 预处理性能

通常来说，在开始计算前，SpMV 的优化方法需要对矩阵数据格式进行一次性地预处理，通常需要将原始数据格式矩阵转为特定的数据格式矩阵.预处理后的矩阵可以在后续多次的SpMV 迭代中重复使用.考虑到实际应用场景中SpMV 的迭代次数可以达到几十甚至上百次，因此通常认为预处理的开销可以被有效分摊.pvSpMV 遵循了类似的设计思路，通过引入预处理环节来完成矩阵的优化.为了尽量降低预处理开销，我们在预处理环节采取极致优化性能的策略，基于C 语言实现了高效的预处理流程.图17 给出了各个优化方法的单线程预处理的开销，预处理开销用单次基准方案的运行时间量化计算.可以看到CVR 的预处理开销最小，平均需要4.9 倍的基准方案运行时间.MKL 的预处理开销最大，平均需要21.7 倍的基准方案运行时间.pvSpMV 的预处理开销略高于CVR，平均需要11 倍的基准方案运行时间.真实场景中SpMV 通常会迭代多次，并考虑到pvSpMV所提供的潜在性能收益，我们认为这一预处理开销是可以接受的.

Fig.17 Evaluation of preprocessing costs of different methods图17 不同方法的预处理开销评估

7 结论

SpMV 在数值计算、大数据分析、图计算领域和智能计算中均是非常重要的计算核心，并且构成了现代高性能处理器的主要性能瓶颈之一.本文通过对SpMV 在现代超标量乱序处理器上的指令流组成和运行情况的分析，总结出3 个关键的性能因素：访存延迟、分支预测错误开销和有效计算密度.基于这一分析结果本文提出，通过对稀疏矩阵的存储格式和计算方法进行修改，可以构建一种具有高度预测性且程序复杂度低的计算核心，充分发挥现代处理器数据预取、分支预测和SIMD 指令集的执行效率，实现访存瓶颈、分支错误和计算效率的全面优化.基于这一思路，本文提出了pvSpMV 这一新型的SpMV计算方法，采用了基于访问串行化的访存优化技术、基于行重排的分支预测优化技术以及具备高有效计算密度的SIMD 优化技术，从而实现了SpMV 的显著性能提升.测试结果显示，pvSpMV 可以在主流Intel高性能处理器上获得与主流商用计算库MKL 相比平均2.6 倍的加速比，相比于现有最先进算法获得平均1.3 倍的加速比.此外，pvSpMV 所需的预处理开销较低，预期具有很好的实际应用价值.

作者贡献声明：夏天与付格林为共同第一作者，其中夏天提出论文思路，设计方法和撰写论文；付格林负责实验设计、数据整理与分析、论文修改；曲劭儒负责代码编写和实验调优；罗中沛负责实验平台搭建；任鹏举负责论文指导和修改.