双网络中影响力凝聚子图发现算法
李 源 杨 森 孙 晶 赵会群 王国仁
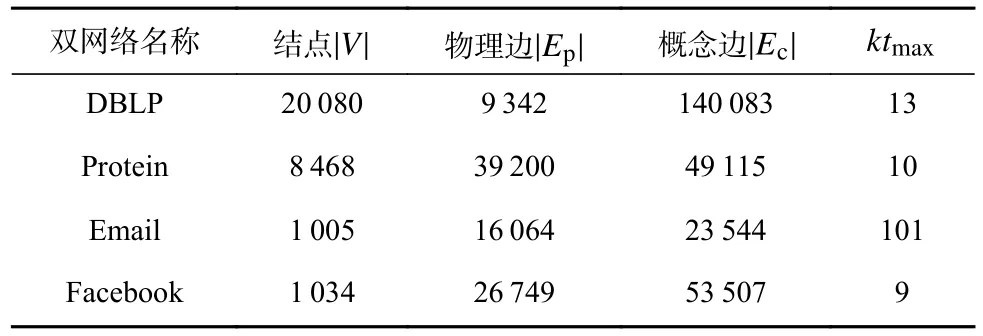
1(北方工业大学信息学院 北京 100144)
2(北京理工大学计算机学院 北京 100081)
(liyuan@ncut.edu.cn)
随着社交媒体、在线社区和移动通信等信息技术的快速发展,这些数据实体积累了大量的数据重复关系[1].鉴于图模型简单而强大的表达能力,这些数据通常被建模为图,图中的结点表示实体,结点之间的边表示实体间的关系.从全局角度看,真实图往往都是稀疏图,但又包含局部关系紧密连接的凝聚子图[2-3],这些凝聚子图中往往包含着人们需要的重要信息.由于大规模真实网络中凝聚子图数量众多,因此寻找具有影响力(重要性)的凝聚子图成为当前的热点问题,有重要现实意义[4-9].目前,许多影响力图模型已经被提出.首先,针对图中单个影响力结点,MIPPLA 模型[10]和EDBC 模型[11]被提出.随后,文献[12-16]提出不同算法用于发现图中影响力凝聚子图.但文献[12-16]所提算法往往仅限于解决单网络中影响力凝聚子图计算问题.
随着应用场景愈发丰富,实体间的关系也变得愈发复杂,单个网络的表达能力已经不能满足需求.对此,Wu 等人[17]提出了一种双网络模型.双网络表示为2 个互补的单网络,这2 个单网络包含相同的结点集合和不同的边集合.其中一个网络表示结点之间真实存在的物理关系,如同事、朋友、家人等,该图称作物理图;另一个网络表示结点之间的概念关系,如相似、喜好程度等通过一些度量函数计算得来的关系,该图称作概念图.因此,双网络中的物理图可表示为不带边权重的无向图,而概念图可表示为带边权重的无向图.值得注意的是,子图权重能够有效表达子图在网络中的影响力.本文聚焦于发现概念图中影响力大且稠密同时物理图内连通的子图.该问题在利用研究者双网络进行研讨会筹备、社交双网络进行商品推荐和生物双网络进行致病基因发现等真实场景中具有广泛应用.
图1 展示了利用研究者双网络进行研讨会筹备的案例.当前的需求是寻找一组研究兴趣相似又彼此认识的研究人员参加研讨会.图1(a)为研究者双网络的物理图,结点之间存在边表示研究者之间合作发表过若干篇论文;图1(b)为概念图,边上的权重表示研究者之间研究兴趣的相似度.从图1 中可以看出,2 个具有很高兴趣相似度的研究人员在现实中有可能并不认识.但是,如果一组具有很高研究兴趣相似度的研究人员同时在物理图中具有连通性,那么这组研究人员就能通过彼此间的物理关系互相认识,因此可以作为一组非常合适的研究人员参加研讨会.
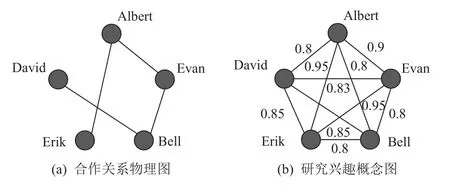
Fig.1 Dual networks of researchers图1 研究者双网络
为了发现双网络在概念图中凝聚而物理图中连通的子图,能够在线性或亚线性时间内求解的k连通核(k-CCO)[18]和k连通truss(k-CT)[19]子图模型相继被提出.但上述模型存在的问题是,仅将概念图构建为边上没有权重的无向图,而没有考虑凝聚子图的重要性,即影响力.Wu 等人[17]提出的概念图中最密集而物理图中连通DCS(dense connected subgraph)子图模型,虽然考虑到概念图中的边权重,但根据最密集子图定义,采用边权重的平均值,并不能有效度量子图的影响力,因为其不能有效消除离群点的影响.例如,一条边的权重过低,它所在子图的密集程度依然可能很大.
针对现有模型存在的问题,本文提出一种双网络中影响力k-连通truss(k-influential connected truss,k-ICT)子图模型.给定双网络G(V,Ep,Ec,Ic)和正整数k,其中Ep为物理图中的边集,Ec为 概念图中的边集,Ic为Ec对应的边影响力集合.k-ICT 子图为双网络中的诱导子图H,当且仅当满足3 个条件:1)在概念图Gc中,H内每条边至少被k-2个三角形包含;2)在概念图Gc中,H内任意2 条边都是三角形连通的,即2条边在同一三角形内或者所在三角形由一系列的三角形连接,其中每2 个相邻三角形都共享一条边;3)在物理图Gp中,H是连通子图.同时,k-ICT 子图H的影响力为,即H的影响力为H中最小边影响力值.这样定义的优势在于最小影响力能够保证H中每条 边的影响力都不小于f(H).如果f(H)值很大,那么子图内每条边的影响力都更大,因此该定义对离群点鲁棒.而且k-ICT 子图带有影响力,当发现影响力较大的子图时,相较k-CT 子图,k-ICT 子图规模更小,可解释性则更强.
根据k-ICT 子图模型,本文重点研究双网络中top-r具有最大影响力k-ICT 子图发现问题.为了解决该问题,需要确定与之相关的单网络中最大影响力子图发现算法是否能够直接用于解决双网络中的最大影响力k-ICT 子图发现问题.最近,文献[12]分别提出了3 种基于在线全局搜索、局部搜索和离线索引的单网络中最大影响力子图发现算法.这3 种算法共同的核心思想是利用结点影响力不变性,迭代删除当前影响力最小的结点,从而使剩余子图的影响力不断提高,直到发现top-r个影响力最大的子图.与本文问题不同的是,上述问题中使用结点的影响力来定义子图的影响力,子图影响力为子图内结点影响力的最小值,而本文工作是使用边影响力来定义子图影响力,如此定义能够更好地反映子图内部结点之间关系的紧密相似性.随后,Zheng 等人[20]提出一种通过不断删除影响力最小边来发现单网络中topr个影响力最大并三角形连通的k-truss 子图(k-truss社区)算法,时间复杂度为O(m1.5),m表示网络中边的数量.但是,通过图2 实例可知,此算法并不可行.
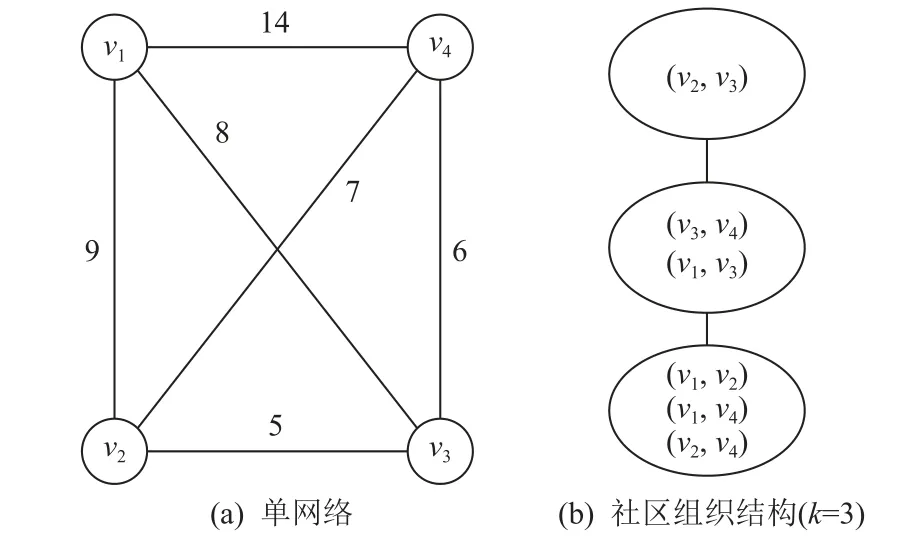
Fig.2 Example of top-2 influential 3-truss community discovery in single network图2 单网络top-2 影响力3-truss 社区发现实例
如图2 所示,文献[20]所述的算法根据图2(a)中的单网络发现的top-2 影响力3-truss 社区为{(v1,v2)(v1,v4)(v2,v4)} 和{(v1,v2)(v1,v4)(v2,v4)(v3,v4)(v1,v3)},影响力分别为7 和6.但通过观察发现,由于带影响力ktruss 社区为诱导子图,根据诱导子图定义只要结点存在并且结点之间在原图中存在边,那么该边也在诱导子图中.删除边 (v2,v3)后,由于剩余图依然是3-truss 社区,所以结点v2和v3依然在子图中并不会导致诱导子图 {v1,v2,v3,v4}影 响力的变化.只有在结点v2或v3被删除时子图影响力才会变化.因此,由边集合{(v1,v2)(v1,v4)(v2,v4)(v3,v4)(v1,v3)}得到的诱导子图真实影响力为5.事实上,由结点集合 {v1,v2,v4} 和{v1,v3,v4}得到的诱导子图才是真正的结果,影响力分别为7 和6.通过后文证明可知单网络中影响力最大ktruss 社区发现问题为NP-难,因此双网络中影响力最大k-ICT 子图发现问题依然为NP-难,多项式时间复杂度内不存在精确解.
为解决双网络中top-r具有最大影响力k-ICT 子图发现问题,本文首先不考虑概念图中影响力,提出CT 分解算法计算每条边的CT 数并对概念图中的边进行CT 等价类划分,然后根据划分的等价类构建CT 概要图索引.利用该索引能够快速还原对于不同给定k值的k-CT 子图作为后续k-ICT 子图发现的候选子图,这样能够大量过滤掉不满足结构条件的结点和边.其次,本文分别提出2 种发现top-r最大影响力k-ICT 子图精确算法:Exact-G kICT 和Exact-LkICT.其中Exact-G kICT 算法从全局k-CT 子图入手,不断枚举删除影响力最小的边和与其连接的结点,直到发现结果子图;而Exact-LkICT 算法则采用从影响力最高的边开始进行局部子图扩展,直到在局部子图中发现top-r最大影响力的k-ICT 子图.
本文的主要贡献点有4 个方面:
1)基于双网络中k-CT 子图,提出了一种带影响力的k-ICT 子图模型,该模型能够保证k-CT 子图在概念图中结点之间具有高度的凝聚性和相似性,并证明影响力最大k-ICT 子图发现问题为NP-难问题;
2)提出一种基于概念图中边CT 等价类划分的概要图CT 索引结构,根据该索引能够针对不同k值快速还原包含k-ICT 子图的候选子图;
3)提出基于全局枚举删除和局部子图扩展策略的精确子图搜索算法Exact-G kICT 和Exact-LkICT,实现高效top-r影响力最大k-ICT 子图发现;
4)使用多个真实和合成数据集进行大量实验验证本文提出算法的高效性和有效性.
1 相关工作
本文相关工作主要包括单网络凝聚子图挖掘、单网络影响力凝聚子图挖掘以及双网络凝聚子图挖掘3 个方面.
1.1 单网络凝聚子图挖掘
单网络凝聚子图挖掘主要是发现图中k-团(kclique)、k-核(k-core)和k-捆(k-truss)等凝聚子图结构.团定义对子图具有最强的约束条件,要求子图中任意2 个结点之间均有边连接.发现极大团是NP-完全问题,Xu 等人[11]提出的BK 改进算法是当前已知最高效的极大团枚举算法.Yuan 等人[21]根据团的定义提出了一种基于索引的社区发现算法.但是由于团的定义过于严格,研究者开始研究基于团松弛的凝聚子图挖掘.k-核结构从结点度的角度对子图进行放松,要求子图内任意结点度数不小于k.文献[22]最先提出一种与图中边数成线性时间复杂度的核分解算法.文献[23-24]分别提出了基于内外存转换的核分解算法.文献[25]提出了在分布式环境下的核分解算法.文献[26]分别提出了在一台个人PC 机上的优化k-核分解算法.Zhang 等人[27]提出了一种基于结点序的k-核维护算法,该算法能够更新最少数量的边.随着应用场景更加复杂,Fang 等人[28]提出了属性图上的k-核算法用于发现子图内结点属性具有相似性的k-核子图.Wang 等人[29]提出了在地理-社交网络中基于半径约束的k-核算法用于发现同时满足子图结构和空间约束的凝聚子图.k-truss 从边的角度对团进行放松,规定k-truss 中每条边至少被k-2个三角形包含.Cohen[30]最先提出k-truss 定义并给出多项式时间复杂度算法.随后Wang 等人[31]提出一种改进的truss 分解算法,通过对边进行排序加速算法效率.文献[32]提出了一种基于图数据库技术的内外存转换k-truss 子图发现算法.k-truss 子图结构还被广泛用于建模社区,文献[33]提出基于最小直径约束的ktruss 社区.文献[34-35]分别利用truss 分解构建图索引,用于发现k-truss 社区.同时,truss 还被扩展应用于不确定图和属性图的社区搜索中[36].k-边连通子图从边连通性对团进行放松,要求每对结点之间至少有k条边独立路径,即任意删除k-1 条边子图仍然连通.文献[37]提出了k-边连通凝聚子图发现和更加高效的优化算法.k-点连通凝聚子图从子图结点间结点连通度进行放松,要求每对结点之间至少有k条结点独立路径,即任意删除k-1个结点子图仍然连通.李源等人[19]提出了允许子图间存在重叠的k-点连通分量定义,并提出自顶向下、自底向上和混合框架的高效子图发现算法.Wen 等人[38]提出了k-点连通分量枚举算法.
1.2 单网络影响力凝聚子图挖掘
单网络影响力凝聚子图发现也称为具有影响力社区发现,目的是要找出网络中影响力最大的凝聚子图.Li 等人[12]将该问题定义为从结点带影响力的网络中发现影响力最大的k-核子图,子图影响力用子图中最小的结点影响力度量.首先,提出一种在线算法,该算法通过不断删除当前图中影响力最小的结点并保持剩余图的结点度数约束,不断发现影响力越来越大的k-核子图.同时对于不同的k值,又提出一种线性索引结构来加速最大影响力k-核子图的发现.接下来,Chen 等人[39]对文献[12]中在线算法进行了优化,在求top-r影响力最大k-核子图时,只计算最后r次迭代中的连通分量.但是文献[12,39]所述的2 种在线算法都利用了整个网络的全局结构.为了更好地优化算法,Bi 等人[40]提出了一种基于局部搜索思想的算法,该算法从影响力最大的结点开始向外逐渐扩展,直到发现最小的包含top-r影响力最大k-核子图的局部子图,该算法的时间复杂度与局部子图大小成线性关系,与全局图的大小无关.文献[12,39,40]所述的算法都是用结点影响力定义子图影响力,Wang 等人[41]在二部图中提出了一种通过边缘权重定义的(α,β)-核社区模型,并根据包含(α,β)-核的最大连通分量建立索引,提出时间复杂度为O(δ×m)的剥离算法与局部扩展算法进行高效地社区搜索.Zheng 等人[20]提出一种通过边影响力定义子图影响力的影响力最大k-truss 社区模型并给出了多项式时间复杂度的top-r影响力最大k-truss 社区发现算法.该算法的思路同样为迭代删除影响力最小边并不断发现影响力更大的k-truss 社区,但是该算法存在的问题是忽略了影响力最大k-truss 社区为诱导子图.如果有诱导子图约束,那么该问题为NP 难问题,详见第3 节中证明.为此,文献[20]提出算法并不能找到topr影响力最大k-truss 社区的精确解.
1.3 双网络凝聚子图挖掘
最近双网络得到研究者的广泛关注[17].双网络G(V,Ep,Ec)包含2 个具有相同结点集但是不同边集的图,其中一个图表示结点间的物理交互关系,另一个图表示结点间的概念交互关系.但是现存的双网络凝聚子图挖掘方法均存在一些问题.首先,Cui 等人[42]提出了k-核连通子图模型,并且提出了高效精确的子图发现算法,但是仅基于k-核的结点度数约束过于松弛,所发现子图可能并不稠密.之后,李源等人[19]提出一种双网络k-truss 连通子图模型,利用ktruss 的三角形结构建模概念图中的稠密区域,因此更加紧致,并提出了3 种高效的子图发现算法.然而在实际应用中,双网络中的概念图应该被建模为权重图,边权重表示结点之间的影响力,因此Wu 等人[17]提出了双网络中的DCS 问题,即发现概念图中密集、物理图中连通的子图,并提出2 种基于不同删除结点策略的贪婪算法来发现近似结果.但是,DCS 子图模型使用概念图中子图边权重的平均值度量子图的密集程度鲁棒性不足,并不能有效地消除离群点的影响,因为即使一条边的权重过低,它所在子图的密集程度依然可能很大.
基于上述问题,本文提出一种双网络中影响力k-连通truss 子图模型,该模型使用子图内边影响力的最小值定义子图影响力,因此对离群点鲁棒.影响力最大k-连通truss 子图能够有效建模双网络中在概念图内影响力最大且稠密,在物理图内连通的子图.
2 概念及问题定义
本节主要介绍双网络相关概念及符号表示,影响力k-连通truss 子图定义,及最大影响力k-连通truss 子图发现问题定义和问题复杂性分析.
2.1 基本概念
给定一个双网络G(V,Ep,Ec,Ic),图Gp(V,Ep)和Gc(V,Ec,Ic)分别表示表示物理图和概念图,其中物理图为无向无影响力图,概念图为无向有影响力图.V为物理图与概念图相同的结点集合,Ep为物理图的边集合,Ec为 概念图的边集合,Ic为 边集Ec对应的边权重集合即边影响力集合.
对于一个无向带边影响力图G(V,E,W),V表示结点集合,n=|V|表 示结点个数;E表示边集合,ei,j表示结点vi和vj之 间存在边,即ei,j=(vi,vj)∈E,m=|E|表示边的个数,W表示边集合E对应的影响力.使用m+n表示图的规模.给定一个图G中的结点u,使用NG(u)表示G中结点u的 邻居集合,用degG(u)表 示G中结点u的度数,并且degG(u)=|NG(u)|.
给定一个结点集合H,G[H]={H,E(H)}表示结点集合H关于图G的诱导子图,如果满足条件:H⊆V并且E(H)={(u,v)|∀u,v∈H∧(u,v)∈E}.下面给出子图影响力的定义.
定义 1.子图影响力.给定一个无向带边影响力图G(V,E,W) 和结点集合H(H⊆V),那么诱导子图G[H]的影响力为边集E(H)中边影响力的最小值,表示为
定义1 中选择影响力最小值而不是选择影响力平均值作为子图影响力,是因为平均值有一个缺点,即它对离群点不够鲁棒.具体地说,一个子图即使f(G[H])很大,但是依然可能包括低影响力结点即离群点[17],这些离群点并不是我们想要的结果.使用边影响力最小值作为子图影响力的好处是如果f(G[H])值很大,可以保证诱导子图内的每一条边的影响力都很大,使得权值小的边不可能出现在影响力大的子图内.因此与平均值相比使用最小值定义子图影响力能够对影响力小的边也就是离群点更加鲁棒.
三角形是构成网络最基本的高阶结构[31].三角形为一个长度为3 的环结构.给定环中的3 个结点u,v,w,那么三角形可以表示为 ∆.根据三角形的定义,给出边的三角形支持度的定义.给定图G中的一条边e=(u,v)∈EG,其支持度用sup(e,G)表 示,sup(e,G)=|{∆|w∈V}|.换句话说,边e的 支持度为图G中包含e的三角形的个数.当没有歧义时,sup(e,G)可以记为sup(e).如果e出 现在三角形 ∆中,则e∈∆.下面给出ktruss 子图定义.
定义 2.k-truss 子图[30]..给定无向带边影响力图G和G的子图G′,G′为一个k-truss 子图,当且仅当每条边e∈E(G′)被至少k-2个三角形包含,即∀e∈E(G′),sup(e,G′)≥k-2,其中k≥2.极大k-truss 子图用Tk表示.
根据定义2,一条边可能属于不同k值的k-truss子图,那么对于一条边e的truss 数可以定义为包含该边使k最大的k-truss 子图的k值,即φ (e)=max{k|E(Tk)}.
由于k-truss 子图[31]可能不连通,下面给出三角形邻接和三角形连通的定义来保证子图的稠密性.
定义 3.三角形邻接[19].给定图G中的2 个三角形∆1和 ∆2,如果 ∆1和 ∆2有一条共同的边,则称 这2 个 三角形邻接,表示为 ∆1∩∆2≠∅.
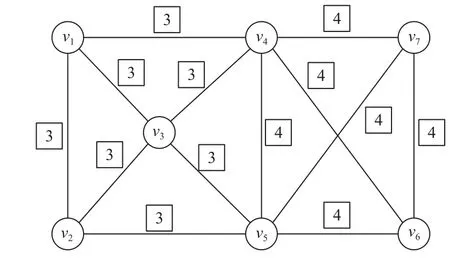
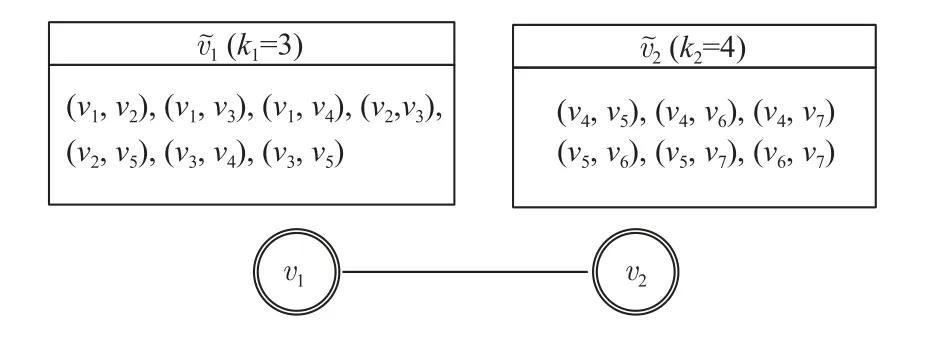
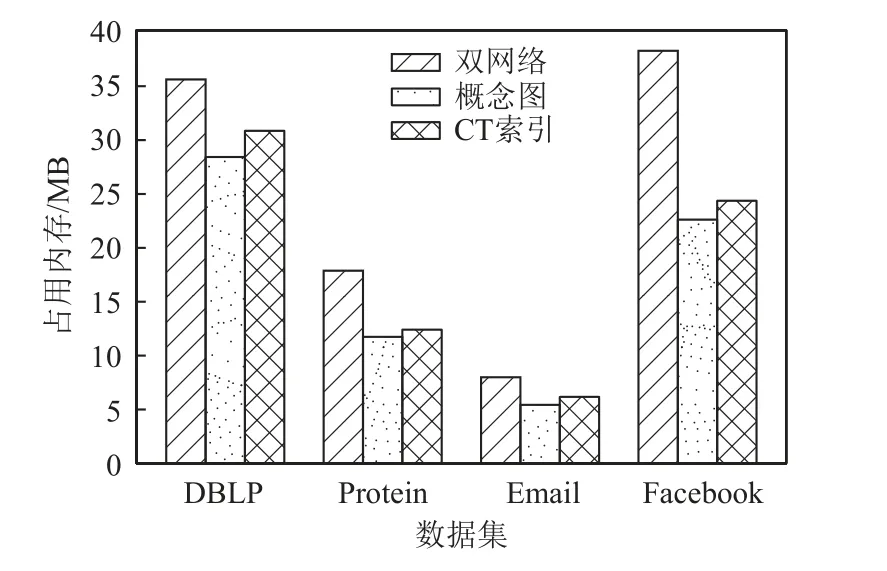
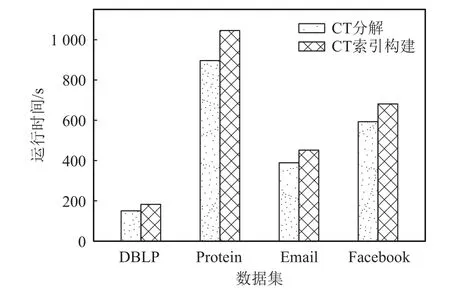
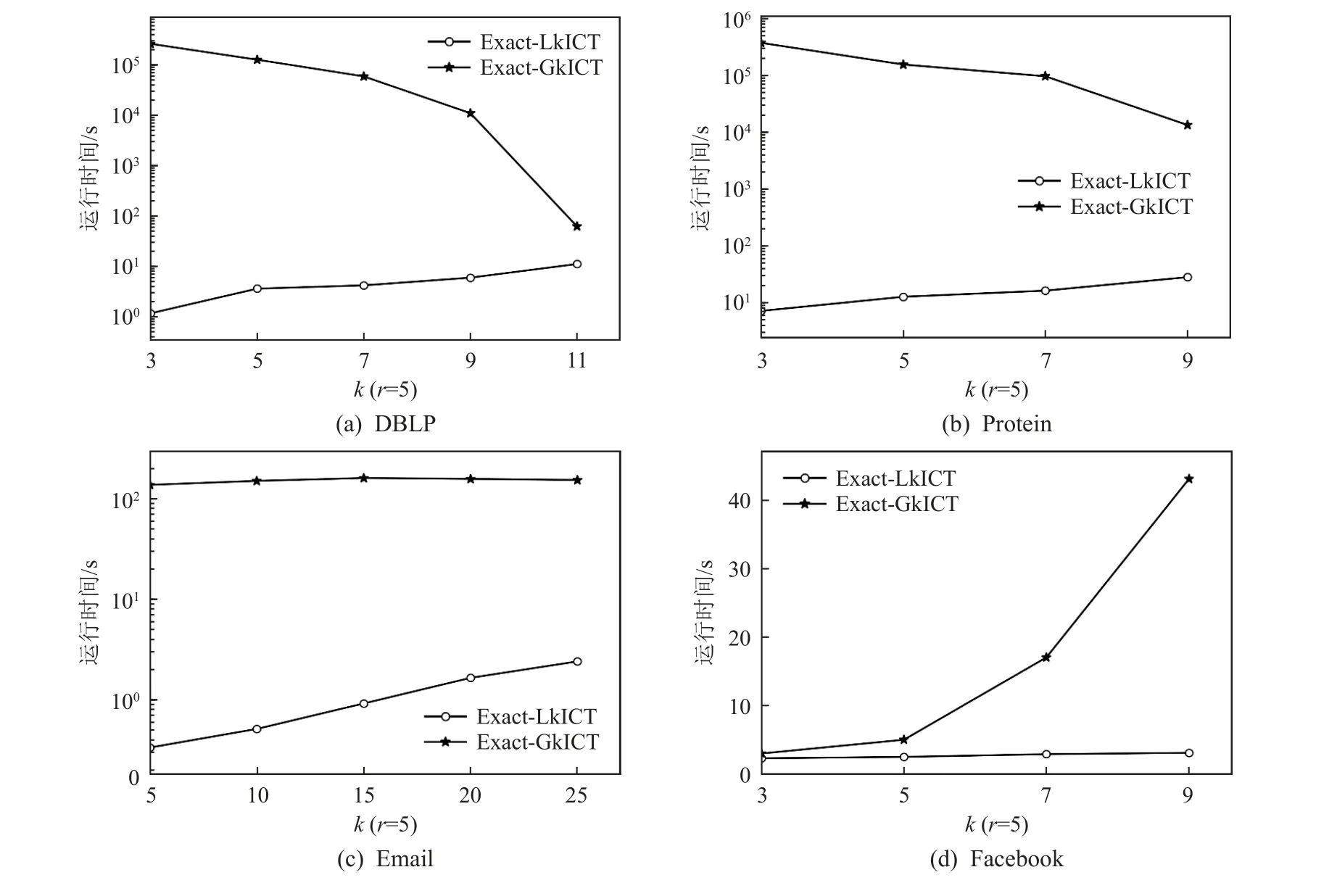
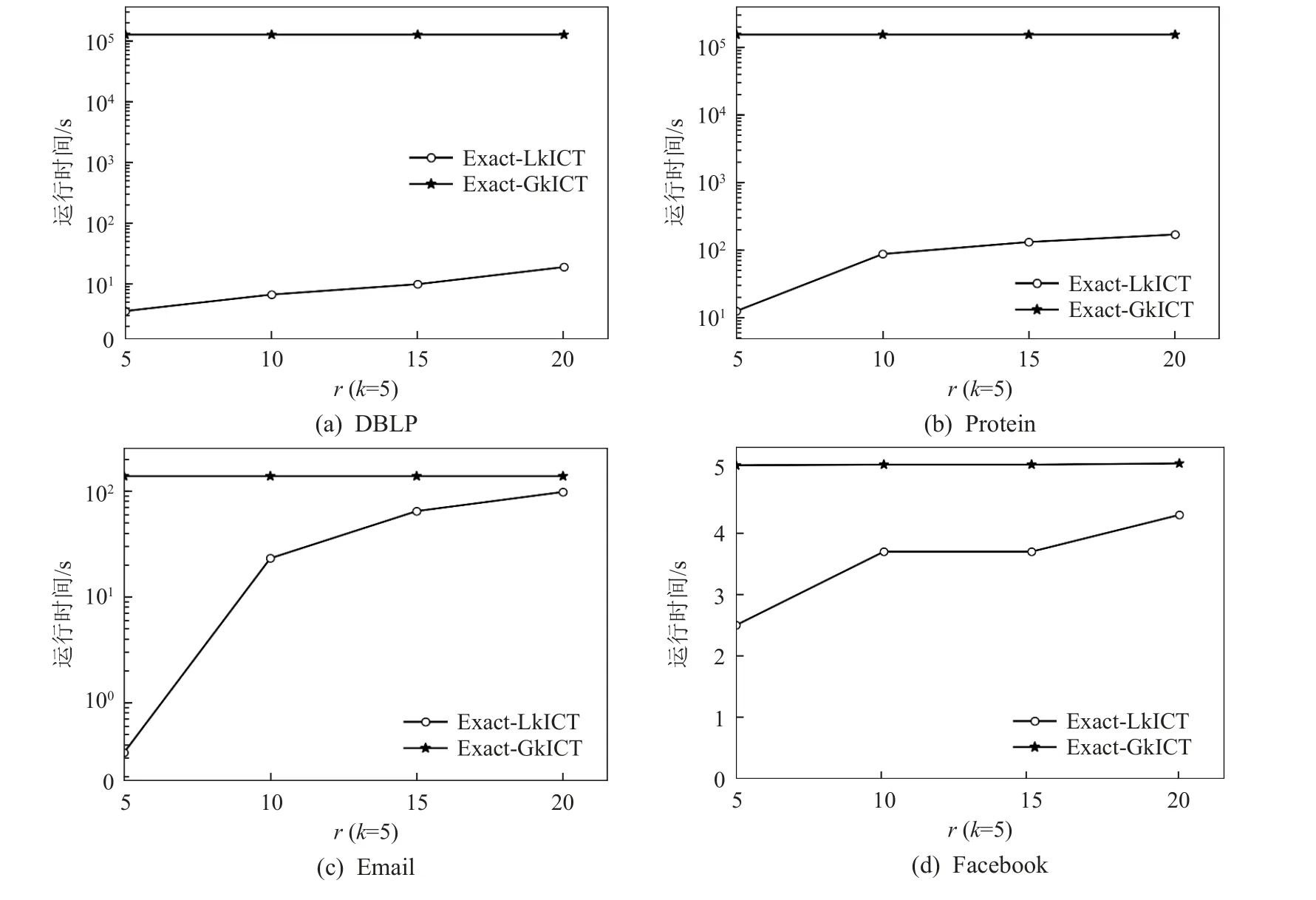
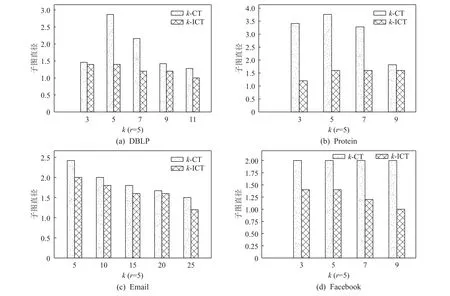
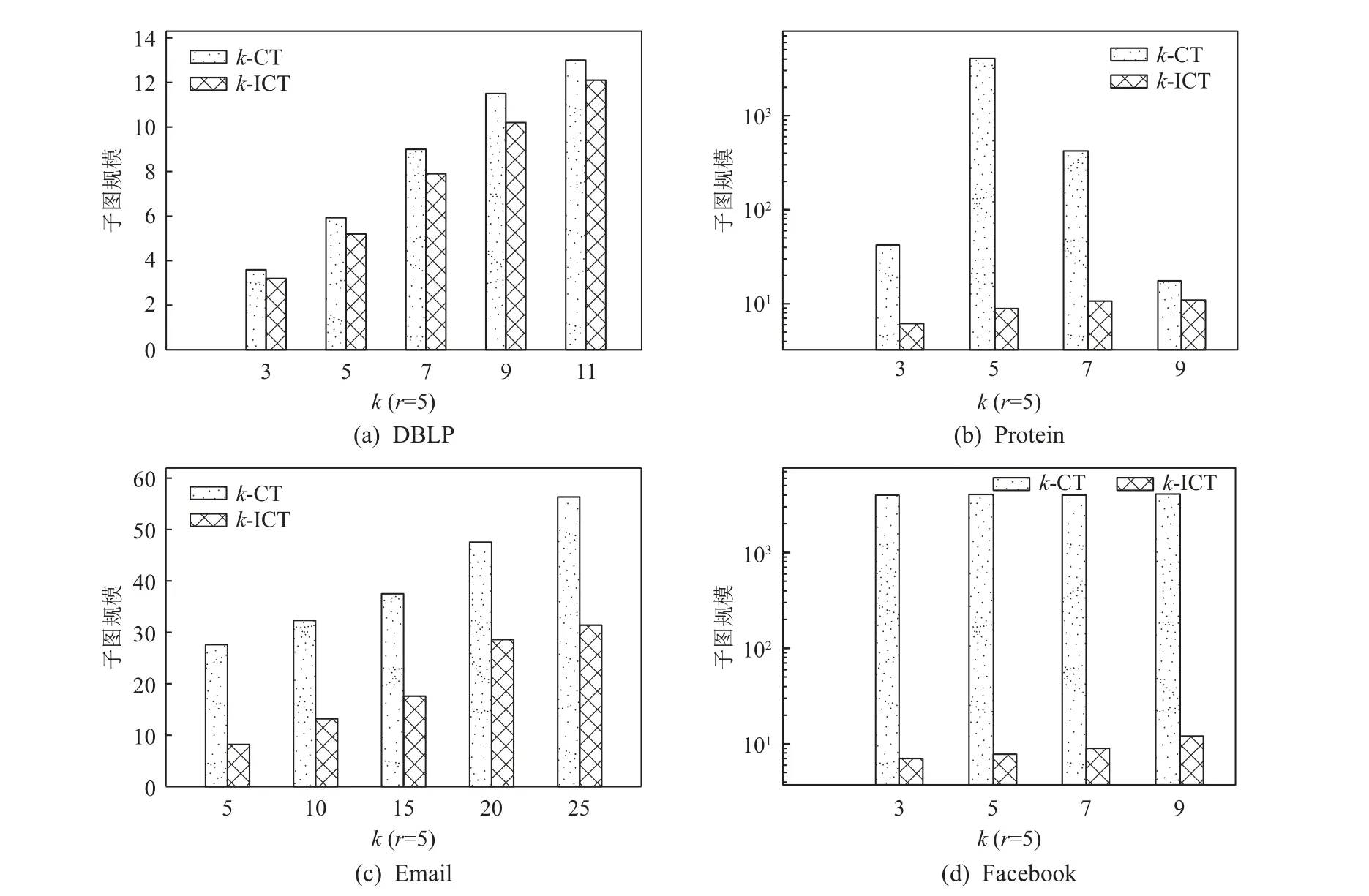
定义 4.三角形连通[19].给定图G中的2 条边e1和e2,如果e1和e2在同一个三角形 ∆中或者存在一系列图G中的三角形 ∆1,∆2,…,∆n,其中n≥2,使得e1∈∆1,e2∈∆n并且对于 1 ≤i 定义 5.k-truss 社区[34].给定一个图G和正整数k(k≥2),一个子图G′⊆G叫作k-truss 社区,满足条件:1)G′为 一个k-truss 子图;2)∀e,e′∈E(G′),e↔e′. 在子图影响力、k-truss 子图和三角形连通定义的基础上,双网络中k-ICT 子图正式定义如下. 定义 6.k-ICT 子 图.给定双网络G(V,Ep,Ec,Ic)正整数k(k≥3)和结点集合H(H⊆V),那么称诱导子图G[H]为k-ICT 子图,满足条件: 1)连通性.Gp[H]在 物理图中连通;Gc[H]中的任意2 条边都是三角形连通的. 2)稠密性.∀e∈Ec(H),sup(e,Gc[H])≥k-2,即Gc[H]为k-truss 子图. 3)正值性.f(Gc[H])>0. 4)极大性.G[H]为满足条件1)2)3)的极大诱导子图,即不存在满足条件1)2)3)的G[H′]∈G使得H⊆H′并且f(Gc[H])≤f(Gc[H′]). 另外给定一个双网络G(V,Ep,Ec,Ic),其最大ICT数记为kmax(G),表示使得k-ICT 子图不为空的最大k值. 图3 给出了双网络的示意图,其中由结点集合{v1,v2,v3,v4}得到的诱导子图为3-ICT 子图,影响力为2;由 {v4,v5,v6,v7}得到的诱导子图为4-ICT 子图.这2个子图全都满足k-ICT 子图定义中的约束条件.但是,由{v1,v3,v4}得到的诱导子图就不是3-ICT,因为该子图不满足子图极大条件约束,存在f({v1,v3,v4})=f({v1,v2,v3,v4})=2. Fig.3 Dual networks图3 双网络 问题1.给定双网络G(V,Ep,Ec,Ic)和正整数k(k≥3),从G中发现top-r影响力最大k-ICT 子图. 下面分析问题1 的复杂性.首先将问题1 简化为单网络中top-1 影响力最大且满足三角形连通的极大k-truss 子图发现问题,即问题2.然后,如果能够证明问题2 是NP-难问题,那么由于问题1 还需要同时考虑子图在物理图中的连通性更加复杂,因此问题1 同样为NP-难问题. 问题 2.给定无向带边影响力图G(V,E,W)和正整数k(k≥3),从图G中发现影响力最大且满足三角形连通约束的极大k-truss 子图. 定理 1.问题2 为NP-难问题. 证明.为了证明问题2 是NP-难的,本文将问题2 归约为另一个著名NP-难的极大团问题.这里考虑极大团问题的判定性版本,图G中是否存在一个结点个数为k的团.首先对问题2 中的图G进行构造,对于图G,任意边e∈E,w(e)=1;对于任意结点u和v,如果u和v在G中不存在边,则添加边 (u,v)并使得w((u,v))=-1.同时,根据图G构建无影响力图G′,使得E′=E.对于图G中满足问题2 中条件的解需要的影响力最大,根据子图影响力定义,该结果子图中不能有负边,因此结果子图内部任意结点间边的影响力必须为1,也就是说该结果子图是由影响力为1 的边构成的团.如果在图G中存在规模大于k的影响力最大且满足三角形连通约束的极大k-truss 子图,那么在图G′中就存在一个规模大于k的团.反过来,如果在图G′中 就存在一个规模大于k的团,那么在图G中也存在一个规模大于k且任意结点之间边影响力都为1 的影响力最大且满足三角形连通约束的极大k-truss 子图.因此,问题2 为NP-难的.证毕.根据定理1,由于问题2 是NP-难的,那么本文要解决的问题1 同样是NP-难问题.在接下来的第3 和第4 节中将详细介绍top-r影响力最大k-ICT 子图发现问题解法. 本节在构建双网络中CT 索引时,调用了文献[19]中的kCT-FIND 算法来发现k-CT 子图.CT 索引为根据k-CT 子图分解构建的一种概要图结构.根据该索引能够更好地确定k-ICT 子图在双网络中更小的范围,从而加速子图发现算法的搜索效率.接下来,首先研究CT 索引设计,然后给出CT 索引构建算法及时间复杂度分析. 为了能够更高效地发现top-r影响力最大的k-ICT 子图,一个关键的问题是先要确定k-ICT 子图可能在双网络G中出现的位置,如果能够预先对双网络进行范围收缩,并且保证收缩后的子图内一定包含k-ICT 子图,那么就能够在更小的子图范围内发现结果,从而提高算法效率.而且参数k的变化对子图发现也有很大影响,为了能够满足对于不同k值的k-ICT 子图的快速发现,构建随k值变化的子图层次结构索引也非常必要.本节提出的CT 索引为根据k-CT 子图等价类划分构建的一种概要图结构.k-CT 子图对k-ICT 子图约束进行了放松,不考虑概念图中边上的影响力,同时不要求是诱导子图.定义7 给出k-CT 子图定义. 定义 7.k-CT 子图[19].给定双网络G(V,Ep,Ec)和正整数k(k≥3),那么子图G′为k-CT 子图当且仅当: 1)G′在概念图中为k-truss 社区; 2)G′在物理图中连通; 3)G′为满足条件1)和条件2)的极大子图. 定理 2.给定k-ICT 子图g,子图g一定被某个k-CT 子图g′所 包含,即g⊆g′. 证明.根据定义6 和定义7,k-ICT 子图除了具备k-CT 子图约束之外,还要求其为诱导子图,也就是说k-ICT 子图在概念图中的任意边支持度都大于等于k-2,相比于k-CT 子图要求更加严格,k-CT 子图包含结点构成的诱导子图可能包含支持度小于k-2的边.同时,k-ICT 子图概念图中边还包含影响力.因此,能够确定如果存在k-ICT 子图g,其一定被某个k-CT子图g′包含.证毕. 根据定义7,一旦得到了所有的k-CT 子图集合,就能从中发现包含的top-r影响力最大k-ICT 子图.因此,CT 索引设计的思想就是通过对CT 子图中的边进行等价类划分,从而能够有效存储不同k值的k-CT 子图.具体做法为:1)对双网络进行k-CT 子图分解,求得双网络概念图中每条边的CT 数;2)根据概念图每条边的CT 数和边与边之间在概念图的三角形连通性,对概念图中的边进行等价类划分. 算法 1.CT 分解(CT_Decomposition). 算法1 给出了CT 分解算法用来计算每条边的CT 数.该算法的核心思想是从双网络中的概念图中不断删除当前支持度最小的边,当一条边被删除时,其所在的k-CT 子图的k值就是该边的CT 数.另外在删除边的同时,需要保持每个子图中结点在物理图中的连通性,如果物理图变得不连通,则需要将物理图中每个连通分量中的结点对应到概念图中,并重新计算每个子图中边的支持度.如此循环直到剩余边都满足条件为止. 具体来讲,首先设置k=2,先找出不在任何k-CT(k≥3)中的边(行①).然后,当Ec≠∅,先找出物理图中的连通分支,概念图中跨不同连通分支的边都被删除,同时每个连通分支内部在概念图中不满足支持度要求的边都被删除(行②~⑱).概念图中的孤立点也被删除(行⑪).对于剩余概念图中的三角形连通分量,如果其在物理图中不连通,还需将其分解为不同子图,放入队列中进行后续处理(行⑭~⑱).当发现所有的(k-1)-CT 子图中的边都被删除,而Ec不为空,则k增加1(行⑳).最后,当Ec中所有边都被删除时,说明每条边的CT 数都已经计算完成并返回结果(行㉓). 接下来分析算法1 的时间复杂度,计算概念图中边的支持度和三角形连通性的时间为O(|Ec|1.5),检查物理图中连通性的时间为O(|Ep|).在一次队列的循环中,连通分量分裂的平均深度为h,最大非空k-CT的k值为km′ax,那么整个算法时间复杂度为O(km′ax×|Ec|1.5×h).图4 给出了图3(b)中每条边的CT 数,如方框内数字所示. Fig.4 Number of CT on each edge in fig.3(b)图4 图3(b)内每条边的CT 数 定义 10.k-三角形.给定一个三角形 ∆uvw⊆Gc,如果三角形中每条边的CT 数都不小于k,即min{τ(u,v),τ(u,w),τ(v,w)}≥k,则 ∆uvw为一个k-三角形. 根据定义12,双网络概念图中的边被划分为一系列互相之间交集为空的等价类,其中每个等价类为包含等价边的集合,该边集合为某个k-CT 子图或子图的组成部分.本节基于k-CT 等价类设计CT 索引.CT 索引可以表示为一个概要图 G(V,E),其中V为超结点集合,E为超边集合 E ⊆V×V.超节点∈V表示一个等价类,超边 (,)∈E表示2 个等价类中的边是三角形连通的,即存在e∈和e′∈使得e↔e′. CT 索引有2 个优点: 1)CT 索引能够保存双网络中所有k-CT 子图(k≥3)结构.原因是根据CT 算法分解能够得到每条边的CT 数,实际上该过程就是求解双网络中对于所有k值的k-CT 子图过程,然后根据边的CT 数和边之间的三角形连通关系就能还原相应的k-CT 子图.在概要图 G中的超节点为等价类边集合,超边为边集之间的三角形连通关系,提供还原k-CT 子图的全部信息,因此能够保存所有k-CT 子图.而且值得注意的是,单个等价类边集内结点集合在物理图中不要求必须连通,只要根据CT 索引还原的k-CT 子图中结点在物理图中连通即可. 2)由于CT 索引概要图中的超节点为双网络概念图中边的划分,因此每条边只出现在1 个超节点中,没有任何存储空间的冗余,占用的空间复杂度为O(|Ec|). 根据CT 索引中概要图 G还原所有k-CT 子图的方法为:首先规定每个等价类对应超节点的值为等价类中边的CT 数记为;然后从图中找出所有≥k的超节点集合 V′;最终 V′在概要图 G中的诱导子图中不同的连通分支就对应所有的k-CT 子图. 图5 展示了图3 中双网络的CT 索引,该索引的概要图中包含2 个超节点和,其中k1=3,k2=4.和之间存在一条超边表示和内的边三角形连通.从图5 可知,双网络中存在一个3-CT 子图和一个4-CT 子图,3-CT 为超节点集合 {,}对应的边集,其在概念图中共包含13 条边;4-CT 为超节点对应的边集,其在概念图中共包含6 条边. Fig.5 CT index of dual-networks in fig.3图5 图3 中双网络CT 索引 算法 2.CT 索引构建(CT_Index_Construction). 接下来研究如何构建CT 索引.算法2 给出了CT 索引的构建过程.算法2 的主要思想是:首先根据每条边的CT 数,从 CT 数小的边开始通过广度优先搜索找到该条边e所在 τ(e)-CT 等价类中的所有边作为一个CT 索引概要图中的超节点;然后根据不同超节点内部边之间的三角形连通性构建超边;最终构建成为CT 索引概要图 G(V,E). CT 索引构建算法详细伪代码如算法2 所示.算法开始是初始化阶段,首先利用CT 分解算法计算概念图中每条边的CT 数,然后根据每条边的CT 数将边e放置到不同的集合 Φk中.对于每条边e∈Ec,维护2 个不同数据结构的变量,其中p为布尔型变量,其表示边e在初始化过程中是否已经被使用过,并且初始化为 false;L表示一个超节点集合,该集合中每个超节点之前已经被处理过,其中 τ() 接下来是索引概要图的构建阶段,算法根据k值从小到大的顺序依次访问 Φk中所有的边,将每条边加入到唯一的超节点中,并且建立超节点之间的超边.首先,对于 Φk中的边e,为其创建一个与之所在k-CT 等价类Ce对应的超节点;然后将边e作为种子对Ec进行宽度优先遍历,将与e为k-三角形连通的边加入到中.在遍历时同时检查是否存在超节点(τ()<τ()=k)通过e与三角形连通,如果存在,则构建超边(,).同时在遍历过程中,如果在k-三角形中存在边e′使得 τ(e′)>k,那么当前e所在的超节点与未来e′所在的超节点三角形连通,并将e加入到e′.L中,等待将来被处理(行⑨~㉜).当边e被处理完成后将其从 Φk和Ec中删除(行㉘),最后返回CT 索引概要图 G(V,E)(行㉜).函 数Edge_Processing用来处理与当前访问边构成k-三角形的其余2 条边,当边CT数等于k,则将该边加入当前超节点,当边CT 数大于k,则将当前超节点的编号记录到边的L队列中(行㉝~㊵). 算法2 中计算所有边CT 数的CT 分解算法时间复杂度为,在索引构建阶段,概念图中的每个三角形刚好被检测一次,因此时间复杂度为概念图中的三角形数量O(|Ec|1.5).最终算法2 的整体时间复杂度为.空间复杂度分析为O(|Ec|). 根据第3 节提出的双网络中CT 索引结构,对于给定的k值,首先根据CT 索引结构中的概要图还原出所有的k-CT 子图,这样就不用每次从整个双网络中寻找top-r最大影响力k-ICT 子图.根据定理2,k-ICT 子图一定存在于某个k-CT 子图中.因此,本节的任务就为从CT 索引获得的k-CT 子图中发现top-r影响力最大的k-ICT 子图. 较k-CT 子图,k-ICT 子图主要有2 点不同:1)k-ICT 子图概念图中带有边影响力;2)k-ICT 子图中概念图为诱导子图.针对第1 点不同,在一个k-CT子图中可能包含若干个k-ICT 子图,因为k-ICT 子图能够满足相同的结构性约束,但是具有不同的子图影响力,因此可以作为不同的k-ICT 子图,也就是说k-ICT子图的规模比满足结构极大条件的k-CT 子图更小.针对第2 点不同,正是由于诱导子图的约束,导致最大影响力k-ICT 子图发现问题为NP-难的.对于诱导子图,单纯的删除边可能并不能改变子图的影响力,只有当子图中的结点发生变化时,子图的影响力才可能发生变化,正是由于该特性给k-ICT 子图发现带来巨大挑战.由于直接根据文献[23]中的方法并不能求得top-r最大影响力k-ICT 子图的精确解,于是本节分别基于全局枚举删除和局部子图扩展思想提出2 种top-r最大影响力k-ICT 子图精确发现算法,称为Exact-G kICT 和Exact-LkICT,并分析2 种算法的复杂度. 4.1.1 Exact-GkICT 算法思想 本节提出了基于全局枚举删除的k-ICT 子图发现算法Exact-G kICT,其主要思想为从包含k-ICT 子图的k-CT 诱导子图中不断删除影响力最小的边,如果删除边后诱导子图的影响力没变化,则删除与影响力最小边邻接的结点,如此往复,直到边集为空停止.在不断的删除边或点的过程中能够在k-CT 诱导子图中发现一系列满足结构性约束的子图,这些子图就称为k-ICT 子图,而且越往后得到的子图影响力越大,最后从得到的候选结果集中输出前r个最大的子图作为top-r最大影响力k-ICT 子图. 算法 3.GExact-kICT 算法. 4.1.2 Exact-G kICT 算法描述 根据4.1.1 节的算法思想,本节提出了完整的Exact-G kICT 算法用于发现top-r最大影响力k-ICT 子图,算法伪代码如算法3 所示.整个算法可以分为3个主要步骤:第1 步,从CT 索引概要图中获得所有的k-CT 子图,使用Gk-CT表示(行②).G k-CT中包含每个k-CT 子图对应的物理图和概念图中的子图.第2 步,通过调用函数FIND-INDUCED-KCT,找到所有k-CT子图中包含的满足k-CT 条件的诱导子图,存放于集合 T 中(行③).由于k-CT 子图中结点集合在双网络中的诱导子图可能包含CT 数小于k-2的边,需要将这些边及其邻接的结点级联删除,直到发现所有满足条件的k-CT 诱导子图.第3 步,通过调用函数FIND-KICT,从当前得到的k-CT 诱导子图集合中找到所有候选的k-ICT 子图(行④).最终输出前r个影响力最大k-ICT 子图作为结果(行⑤). 函数FIND-INDUCED-KCT用于发现k-CT 子图中所有包含的k-CT 诱导子图.首先如果对于当前的k-CT 子图中结点得到的诱导子图中不包含任何CT 数小于k-2的边,则可直接将该子图放入 T中(行⑧~⑨);否则,需要分别删除不满足条件边对应的2 个结点,然后再递归调用函数FIND-INDUCED-KCT,从删除结点后的子图中发现k-CT 诱导子图,最终结果都存放于 T 中(行⑪~⑮).整个循环过程直至Gk-CT中不存在CT 数小于2 的边为止,得到的结果都是k-CT诱导子图(行⑦~⑯). 函数FIND-KICT用于发现k-CT 诱导子图中包含的k-ICT 子图.首先,当前的所有k-CT 诱导子图自身就为k-ICT 子图,计算子图影响力 T 并将 T 放入候选结果集 Rcand中(行⑰).然后当 T不为空时,不断从中删除影响力最小的边,并得到新的影响力更大的k-ICT子图(行⑱~㉞).在具体实现过程中可将所有子图按照影响力从小到大顺序存放在优先队列中,并通过最好优先方式进行处理.在删除影响力最小的边以及随之不满足条件的边后,如果子图中三角形连通分量数和结点没有变化,则需要进一步分别删除影响力最小边对应的结点,并找到子图中的k-ICT 子图(行㉑~㉗).否则,对当前删除边后子图的每个三角形连通分量进行处理,找到其中的k-ICT 子图(行㉘~㉛).同时分别将获得的k-ICT 子图放入 T 和 Rcand中. 算法Exact-G kICT 的时间复杂度主要受k-CT 子图Gk-CT的大小影响,因为结果子图为诱导子图,只有当子图中结点发生变化,子图影响力才可能变化.在删除影响力最小边时,需要枚举删除边相邻的2 个结点.在最坏情况下需要枚举删除每条边对应的结点,因此最坏时间复杂度为O(2|Vk-CT|×|Ek-CT|1.5).但是在实际情况中由于边或结点的删除会引起其他边和结点的级联删除,因此算法实际时间复杂度要远小于最坏时间复杂度. 接下来使用图3 中的双网络来演示算法Exact-GkICT,假设要发现top-2 最大影响力3-ICT 子图.首先整个双网络G就为一个3-CT 诱导子图,同样为一个3-ICT 子图,影响力f(Gc)=1.接下来删除影响力最小的边 (v3,v5),其删除导致边 (v2,v5)的删除.这时整个图划分为2 个三角形连通分量{v1,v2,v3,v4}和{v4,v5,v6,v7},同样也是2 个3-ICT 子图,影响力分别为2 和5.然后分别从这2 个3-ICT 子图中删除最小影响力的边,值得注意的是,在删除边 (v5,v6)时,需要分别枚举删除结点v5和v6,这样边 (v5,v6)才能够在诱导子图中被真正删除.最终得到的结果为由结点集合{v1,v2,v3}和{v4,v5,v7}诱导构成的3-ICT 子图,对应影响力分别为10 和7. 4.2.1 Exact-LkICT 算法思想 在4.1 节中提出的全局枚举删除算法Exact-GkICT 中可以看出,影响力最大的子图往往在算法最后才能计算出来.原因是全局算法首先删除影响力最小的边,产生的子图影响力是升序排列.但是,当想要发现top-r最大影响力k-ICT 子图中的r值较小时,算法Exact-G kICT 仍然需要枚举删除整个k-CT 子图中的结点,导致算法效率较低.例如,为了发现top-1最大影响力k-ICT 子图,需要首先发现top-n,top-(n-1),…,top-2 影响力最大的子图. 为了能够更快地发现较小r值的top-r最大影响力k-ICT 子图,本节提出了一种基于局部子图扩展的算法Exact-LkICT.该算法的主要思想是从包含k-ICT子图的k-CT 子图对应概念图中影响力最大的边入手,将边影响力按照从大到小进行排序.然后,确定能够包含top-r最大影响力k-ICT 子图最小边集合的规模,也就是初始局部子图的大小.这样就可以根据边的影响力由大到小从k-CT 子图不断向局部子图中加入边,如果当前的局部子图中包含k-ICT 子图的数量小于r,则相应扩大局部子图规模,直到该局部子图中包含top-r最大影响力k-ICT 子图为止. 为了保证算法Exact-LkICT 的顺利执行,一个很重要的问题就是确定初始局部子图的规模,需要估计可能包含top-r最大影响力k-ICT 子图的局部子图内边集合的大小,也就是该局部子图内至少存在相同的边数量才可能包含结果子图集合.定理3 给出证明. 算法 4.Exact-LkICT. 4.2.2 Exact-LkICT 算法描述 根据4.2.1 节中给出的算法思想,本节提出局部扩展的Exact-LkICT 算法,伪代码如算法4 所示.首先,对变量进行初始化,其中 δ表示局部子图规模扩展的倍数(行①).其次,根据CT 索引中的概要图获得k-CT 子图Gk-CT.因为需要将Gk-CT的概念图中边按照影响力由大到小向局部子图中添加,因此对Ec(Gk-CT) 中的边按照影响力进行降序排序(行③).然后,给定G1为初始局部子图,该子图中包含Ec(Gk-CT) 中前k×(k-1)/2+(r-1)×k条影响力最大的边(行④).接下来,当|Ec(Gi)|≤|Ec(Gk-CT) |且r′>0时,说明从当前局部子图中发现的结果还不够r个,需要对当前子图继续进行扩展,从Ec(Gk-CT) 中接续向当前子图中增量加入影响力大的边,直到局部子图规模大于Gk-CT或者结果子图数量达到r为止(行⑤~⑰). 下面分别介绍函数FIND-INDUCED-KCT-R(行⑥)和函数FIND-KICT-R(行⑦).函数FIND-INDUCEDKCT-R与算法3 中函数FIND-INDUCED-KCT功能类似,从当前局部双网络Gi中发现k-CT 诱导子图.假定Gi中影响力最小边对应的影响力为wi,区别在于函数FIND-INDUCED-KCT-R需要从Gi概念图对应的诱导子图中额外删除影响力小于wi的边.同时如果在删除边或结点的过程中发现已经开始删除Gi-1中的边或点则停止,因为此时子图中已经不可能包含新的诱导子图,目的是不重复发现之前循环中已经发现的诱导子图.对于函数FIND-KICT-R,同样只需发现当前Gi中新包含的k-ICT 子图,而不是重复发现之前Gt(t 算法Exact-LkICT 采用增量计算方式不断对当前局部子图进行扩展,保证每个top-r最大影响力k-ICT 子图都能被发现且仅被发现一次.该算法的时间复杂度与最后发现的包含top-r结果的局部双网络Gi中结点数量有关,最坏情况下时间复杂度为O(2|Vi|×|Ei|1.5).由此可以看出,算法Exact-LkICT 的时间复杂度仅与包含结果的双网络子图大小有关而与整个Gk-CT规模无关,且当r值越小时,算法Exact-LkICT 效率更高. 下面使用图3 中的双网络来演示算法Exact-LkICT,假设要发现top-1 最大影响力3-ICT 子图.首先,根据CT 索引获得3-CT 子图,其概念子图中的边为整个概念图中的边;然后按照影响力对概念图中的边由大到小进行排序,并将影响力最大的3 条边即 (v4,v7),(v3,v4) 和 (v1,v3) 加入到G1中(w1=12),并得到结点集合 {v1,v3,v4,v7}在双网络中的诱导子图.由于该诱导子图包含边 (v1,v4),w((v1,v4))=2 本文使用真实数据集对算法进行测试,评估的算法包括CT 索引构建、Exact-G kICT 和Exact-LkICT.实验软硬件环境为:Windows 10 家庭版操作系统,AMD Ryzen 74800H with Radeon Graphics的CPU,主频2.90 GHz,16 GB 内存,1 TB 硬盘;开发平台为JetBrains PyCharm 2020,开发语言为Python 3.7. 实验采用的4 个真实数据集包括:DBLP,Protein,Email,Facebook.数据集统计信息如表1 所示. Table 1 The Real Datasets表1 真实数据集 1)DBLP 双网络.从DBLP 双网络①https://dblp.uni-trier.de/中提取SIGMOD,VLDB,ICDE,CIKM,EDBT,DASFAA,KDD,ICDM,SDM,WSDM,PAKDD 等11 个数据库和数据挖掘领域会议.物理图中结点之间存在边则表示2 位作者曾经至少共同发表过1 篇论文;概念图中的边表示2 位作者的研究兴趣相似度.边影响力通过使用余弦函数度量作者间论文关键字相似度获得. 2)Protein 双网络[17].Protein 双网络中结点为蛋白质对应基因.物理图中边表示2 个基因共调控关系.概念图中边表示基因与高血压复杂疾病的遗传交互关系,边影响力表示统计显著值. 3)Email 双网络[43].Email 双网络根据研究机构电子邮件数据构建.结点表示电子邮件用户,物理图中边表示2 个用户间发送过邮件,概念图中边表示2个用户属于相同部门.边影响力表示2 个用户属于共同的部门数量与总部门数量的比值. 4)Facebook 双网络[43].Facebook 双网络中结点表示用户.物理图中边表示2 个用户具有相同的政治背景,概念图中边表示2 个用户具有相似的爱好.边影响力表示兴趣爱好的相似度. 表1 中ktmax表示该数据集的最大k-truss 值.由于k-ICT 的正值性有可能出现ktmax与最终选取k值相差过大的情况.双网络根据各个数据集ktmax值的不同并结合实际情况,在实验中对于DBLP 数据集设置参数k值取值范围为 {3,5,7,9,11},Facebook 数据集的k值取值范围为{3,5,7,9},Protein 数据集的k值取值范围为 {3,5,7,9},Email 数据集的k值取值范围为{5,10,15,20,25}.对于参数r,实验取值范围为 {5,10,15,20,25}.对于算法Exact-LkICT 中的子图规模扩展值 δ设置为2,本次实验中 δ不作为参数. 本节主要评估CT 索引的性能以及k-ICT 子图发现算法的效率和可扩展性. 5.3.1 CT 索引性能分析 本节主要评估CT 索引占用内存大小和构建CT索引的时间开销. 首先,图6 展示了CT 索引在不同数据集上的内存大小,同时给出了与数据集对应双网络和概念图占用索引大小的比较.通过图6 可以看出,CT 索引占用内存要小于双网络占用内存,而且只稍稍大于概念图占用内存.这是因为CT 索引的概要图结构规模非常小,而且每个超节点对应双网络概念图中边的划分中的一个子集,而所有超节点刚好对应概念图中的所有边,因此占用内存主要受概念图大小的影响,在空间上非常紧凑、没有冗余. Fig.6 Memory usage of CT index on different datasets图6 CT 索引在不同数据集上内存占用 其次,图7 展示了在不同数据集上CT 索引的构建时间.并且在相同数据集中给出了CT 索引构建的主要构成部分,边CT 数的CT 分解算法运行时间的比较.从图7 中可以看出,构建CT 索引的时间主要花费在CT 分解上.因为CT 分解算法不仅要计算概念图中边的支持度,同时还要保证子图在物理图中连通,因此较为耗时.一旦求得概念图中边的CT 数,CT 构建算法中的后续部分仅需对概念图中的三角形进行遍历,就能求出概要图中超节点对应的等价类以及构建超节点之间的超边. Fig.7 CT index construction time on different datasets图7 CT 索引在不同数据集上的构建时间 5.3.2 top-r最大影响力k-ICT 子图发现算法效率 本节主要评估算法Exact-G kICT 和算法Exact-LkICT 发现top-r最大影响力k-ICT 子图的效率. 首先,图8 展示了算法Exact-G kICT 和算法Exact-LkICT 在固定r值的情况下随k值变化的运行时间.从图8 中可以看出,在所有的真实数据集中,算法Exact-LkICT 比算法Exact-G kICT 运行速度更快.造成这种现象的原因是算法Exact-LkICT 在发现top-r最大影响力k-ICT 子图时,不需要使用全局k-CT 子图,而只需知晓结果子图的大小,因此运行速度更快.这种现象在k值较小时更为明显,算法Exact-LkICT 要比Exact-GkICT 快至少1 个数量级.反观算法Exact-GkICT,每次都需要从全局k-CT 子图中删除边或点来获得最终结果.对于算法Exact-G kICT,在一些数据集上的运行速度随k的增加而变快,原因是全局k-CT子图的规模随k的增加而变小.对于算法Exact-LkICT,其运行时间随k的增加略微增加,原因是随k的增加结果子图规模增大. Fig.8 The runtime with varying k in different real datasets图8 不同真实数据集中随k 值变化的运行时间 其次,图9 展示了算法Exact-G kICT 和算法Exact-LkICT 在固定k值的情况下随r值变化的运行时间.从图9 能够看出,在所有真实数据集中,算法Exact-LkICT 的运行时间要远低于算法Exact-G kICT 的运行时间.原因与图8 中实验分析一致.但是,对于算法Exact-G kICT,其运行时间随r值变化基本没有变化.原因是在k值固定的情况下k-CT 子图规模未发生变化,而且算法Exact-G kICT 发现k-ICT 子图的影响力值由小逐渐变大,算法最后才能得到最大影响力的子图.为获得top-r个最大影响力子图仍需运行整个算法,r值的变化只能引起输出结果数量的变化,运行时间变化可忽略不计.对于算法Exact-LkICT,其运行时间随r值增加而增加,原因是需要从规模更大的局部子图中来发现更多的结果子图,因此运行时间更长,但总运行时间仍远小于算法Exact-G kICT. Fig.9 The runtime with varying r in different real datasets图9 不同真实数据集中随r 值变化的运行时间 从k-ICT 子图定义能够发现k-ICT 子图包含于k-CT 子图中,k-CT 子图可以被视为k-ICT 子图的候选集合.相较k-CT 子图,最大影响力k-ICT 子图结构更加紧密且规模更小,能够表示k-CT 子图中最核心且重要的子图区域. 本节使用概念图直径和图中结点数量来比较k-ICT 子图和k-CT 子图模型的紧密性.其中子图直径定义为图中任意2 个结点间最短路径中的最大值,即,其中distance(u,v)表示结点u和v在图中的最短距离.子图直径值越小说明图越紧密.另外,使用图结点数量 |V|表示子图规模,结点数量越少说明子图规模越小. 图10 展示了k-ICT 子图和k-CT 子图在不同真实双网络数据集中直径大小的比较.总体来看,对于不同的k值,k-ICT 子图直径要小于k-CT 子图直径,原因是k-ICT 子图虽然结构约束和k-CT 子图一样强,但是规模更小.k-ICT 为k-CT 的子图,表示k-CT 子图中影响力最大且更为核心的区域,因此结点之间的距离更近、直径更小.另外,从图10 中能够发现,对于k-CT 子图,当k值较小时,子图直径有可能更小,这是因为图中有许多直径非常小的k-CT 子图,在计算直径平均值时,降低了规模较大k-CT 子图的直径.随着k值变大,这些小规模k-CT 子图被不断过滤掉,因此子图直径反而变大.但是,当k值继续增大时,子图约束更强,直径又开始变小.对于k-ICT 子图,其随k值变化直径变化并不明显,这是因为k-ICT 子图始终保持较小规模. Fig.10 Subgraph diameter in different real dual networks图10 不同真实双网络中子图直径 图11 展示了不同真实双网络中k-CT 子图和k-ICT 子图在不同k值下的规模.从图11 中能够看出,k-ICT 子图规模整体小于k-CT 子图规模,只有在DBLP 双网络中两者规模相近.原因是k-ICT 子图为k-CT 子图中影响力最大且同样满足结构约束的子图,所以规模更小.在DBLP 双网络中k-CT 子图规模本身较小,因此和k-ICT 子图规模相差并不明显,但是对于其他双网络规模差距非常明显.对于k-CT 子图,DBLP 和Email 双网络中子图平均规模随k值增大.Protein 双网络规模呈先增大后减小趋势,原因是随k值增大,过滤掉规模较小的k-CT 子图,因此子图规模更大.但是当k值更大时,当前规模大的子图被打散为许多小的子图,因此规模变小.而Facebook 双网络则始终存在一个很大的k-CT 子图,总之,与双网络的结构分布有关.对于k-ICT 子图,子图规模随k值增大而增加,同时子图中顶点数量与k值大小在相同数量级.原因是k-ICT 子图在子图影响力的约束下定义结构上的极大性,最大影响力k-ICT 子图规模往往很小,但需要包含至少k个结点. Fig.11 Subgraph scale in different real dual networks图11 不同真实双网络中子图规模 图12 展示了Protein 双网络中top-1 最大影响力9-ICT 子图.Protein 双网络概念图中边表示2 个基因与高血压疾病的交互显著程度,边影响力越大说明具有越强的统计显著性;物理图中边表示2 个基因在蛋白质交互网络中具有真实的物理共调控作用.图12 中子图的概念图不仅稠密而且具有很高的边影响力,并且在物理图中连通,说明该子图与高血压疾病具有显著关联关系.例如,文献[44]中报道基因STK24(又名MST3)能够调节血液中钠离子的浓度,这与钠离子表达增强引起的遗传性高血压具有直接关系.文献[45]中报道STRN 基因多态性变异与血压正常和高血压患者的盐敏感性血压相关.PPP2 基因族(PPP2R1A 和PPP2CA)[46]是人类心脏功能的子单元,而心脏功能对血压有直接影响.文献[47]中报道基因CTTNBP2 与血压的遗传因素有直接关系.而且STK24,STRN,STRN3,PDCD10 等基因都在相同的控制心血管的功能团中[48].因此,本文发现的Protein 双网络中真实结果具有非常强的生物学意义.另外,k-ICT 子图规模较k-CT 子图更小,具有更强的可解释性. 本文提出一种双网络中k-ICT 子图模型,该模型利用子图中最小边影响力定义子图影响力具有更强鲁棒性.影响力最大k-ICT 子图能够有效反映子图在网络中的重要性且规模更小同时具备更强解释性.与当前k-truss 和k-CT 模型相比得出,诱导子图的约束条件使得发现影响力最大k-ICT 子图问题为NP-难的.为此,首先提出一种基于概念图中边CT 等价类划分的CT 索引结构,根据索引概要图能够快速发现包含所有k-ICT 子图的候选子图,避免每次都从整个双网络中发现k-ICT 子图.其次,分别提出基于全局枚举删除策略和局部子图扩展策略的精确算法Exact-GkICT 和Exact-LkICT,发现top-r最大影响力k-ICT子图.由于Exact-LkICT 算法仅需从影响力较大边集合构成的子图中发现满足条件的结果,因此当r值较小时运行效率更高.最后,在真实数据集上的实验验证了本文的模型和算法的高效性和有效性.未来工作将设计更高效的近似算法来发现近似k-ICT 子图. 作者贡献声明:李源负责算法设计和论文撰写;杨森负责算法编写和实验;孙晶负责实验设计和论文撰写;赵会群负责论文框架设计和论文修改;王国仁负责论文框架设计.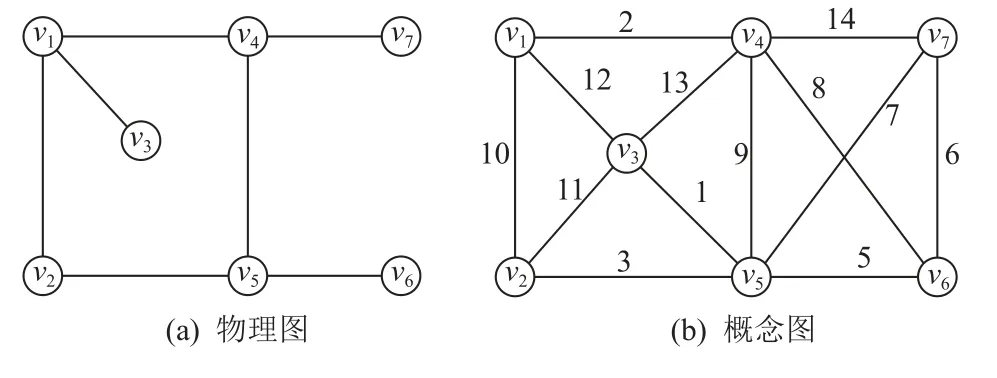
2.2 问题定义
3 双网络中CT 索引结构
3.1 CT 等价类划分
3.2 CT 索引设计与构建
4 双网络中k-ICT 子图发现算法
4.1 全局k -ICT 子图发现算法Exact-GkICT
4.2 局部k -ICT 子图发现算法Exact-LkICT
5 实验结果与分析
5.1 实验环境配置
5.2 实验数据集和参数配置
5.3 算法性能分析
5.4 算法有效性分析
5.5 案例分析
6 结论

